ABAQUS二次開發在骨重建仿真中的應用

井 野，呂林蔚*，宋 陽，張春秋

（天津理工大學a.天津市先進機電系統設計與智能控制重點實驗室，b.機電工程國家級實驗教學示范中心，天津300384）

骨骼是支撐人體結構的重要器官，其主要功能是為人體承擔各種外力載荷[1]。WOLFF和JOUOS[2]認為骨具有力學功能適應性，應力分布與骨骼的結構之間存在一定聯系。骨組織可以通過重建作用，根據外力載荷的不同，改變其自身結構，以適應新的力學環境。根據WOLFF定律[3-4]，骨重建是通過骨形成和骨吸收調節骨組織的含量并試圖用最少的骨量來獲得最大的結構剛度，以滿足力學性能要求的過程。通過這種方式，對骨組織結構不斷進行優化，防止骨骼中微損傷的積累。并在一定程度上也會引起骨宏觀尺度力學特性（例如密度和剛度）的變化。

自從WOLFF定律被提出以來，通過建立骨重建的數學模型，定量地模擬力學環境對骨量調節的影響過程，逐漸成為了研究重點[5]。現有的骨重建數值仿真研究，主要是以MULLENDER等[6]根據骨功能適應性理論提出的自適應模型以及WEINANS等[7]改進Fyhrie和FYHRIE[8]所建立的骨自優化方程為基礎。其中自適應模型是一個可以依據所受力學激勵與穩態之間的差值而進行調整和改變的反饋系統。而骨自優化方程實際上是根據外部載荷情況，通過調整密度，以獲得單位骨量應變能密度（strain energy density，SED）的恒定預設值的目標函數。GONG等[9]通過高階非線性方程來調控骨重建過程，將定量骨重建理論拓展到椎體邊緣骨質增生的形成，證明了骨質增生等骨形態異常也符合自適應重建過程，骨形態異常與力學環境有關。此外，在許多研究中[10-11]，表觀密度被認為是確定骨組織力學性能及影響骨重建過程的重要變量，可以用其描述及評價骨強度和剛度的變化。并且由于以前的研究已經證明了維持骨量與骨組織中的局部應變值之間有密切的聯系，因此也有學者[12]利用最小化局部應變能密度的求解，來描述骨重建過程。

隨著計算機技術的發展，有限元法（finite element method，FEM）成為骨生物力學研究的重要手段[13]。KUMAR等[14]基于ANSYS軟件，分析了正常行走、站立、跑步和跳躍活動中的股骨應力情況，用來預測骨折風險及選擇人造骨材料。YANG等[15]采用不同的彈性模量與密度關系，研究二維股骨近端的骨重建情況，發現兩者參數的選擇會對骨重建結果產生影響。

ABAQUS軟件是功能強大的有限元分析工具，具有極強的通用性和仿真計算能力[16]。本研究通過Python腳本語言對ABAQUS軟件進行二次開發，把基于應變能密度理論的骨重建自優化方程進行編程，建立骨組織重建模型，來分析外部載荷作用下骨結構的變化，預測骨組織的密度分布。希望證明基于Python腳本語言的骨重建程序算法是一種可靠的有限元計算手段，為今后的骨重建數值仿真研究提供新的方法。

1 理論與方法

1.1 骨自優化理論

本研究的骨重建數值仿真是以有限元技術為手段，以應變能準則為基礎的骨自優化理論，模擬骨組織受力重建過程。總體思路是通過骨組織表觀密度的變化率控制其重建，利用有限元法迭代計算出模型各個節點力學激勵數值，與參考值比較，判斷是否達到平衡態。骨重建數值模擬流程如圖1所示。

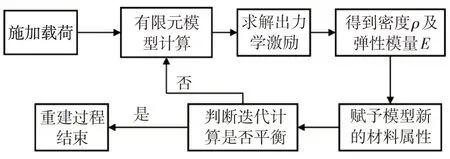
圖1 骨重建數值模擬流程圖Fig.1 Flow chart of numerical simulation of bone remodeling

根據FROST[17]提出的骨組織中存在著“力學調控穩態機制”，當施加外部載荷使骨組織內部的力學環境發生改變時，骨細胞原本處于的最佳生理平衡狀態即被破壞，而應力、應變及應變能密度等力學特性因素會受到其影響，與平衡時的穩態值存在差值，此時骨組織將啟動重建程序，使其再次重新回到平衡狀態。FYHRIE和CARTER[18]利用數學方法將Frost的力學穩態理論參數化，提出了骨自優化控制方程，用來描述骨組織表觀密度變化率為：

式中，ρ為骨組織表觀密度，可以表征骨組織內部的結構特性；B為骨重建變化率的時間常數，與骨組織本身有關；S為力學激勵，可以選擇包括等效應力、等效應變及應變能密度在內的力學特性因素；K為力學穩態的參考值常數。

WEINANS等[19]將前面學者的相關研究統一為骨自優化理論，把單位質量的應變能密度Un/ρ作為式（1）中的力學激勵S為：

式中，Un為應變能密度，E為骨的表觀彈性模量，C為模量-密度常數，r為影響指數，ρcb為皮質骨的表觀密度，假定為最大骨密度。

上述骨自優化理論的數學表達是本文研究的編程依據，是定量研究骨重建過程的理論基礎。

1.2 ABAQUS的二次開發

本研究對ABAQUS進行二次開發，編寫骨重建算法程序，為提高有限元仿真的效率。

1.2.1 前處理部分

前處理部分的創建部件、定義裝配件、設置分析功能、定義載荷及邊界條件和劃分網格在ABAQUS主界面中完成。將材料屬性參數編譯成程序，創建截面屬性，并將其賦予給部件。根據骨自優化理論數學表達式（3），在每次骨重建迭代計算之前設定密度、彈性模量和泊松比等材料屬性。將初始密度假設為1.74 g/cm3，彈性模量與密度有關，取泊松比為0.3。

1.2.2 計算過程

前處理過程完成后，執行作業模塊，創建作業、提交運算及等待計算結束。根據骨自優化控制方程，將力學激勵S設置為Un/ρ，即骨單位質量的應變能密度，取參考值K為0.153 7，時間常數B設置為1[20]，則目標函數轉化為：

密度的變化率隨骨組織內部應力的分布情況而改變，最終目標是令密度的變化率dρ/dt=0，即調整單位大小的應變能密度達到平衡態預設的K值。滿足平衡條件，迭代優化結束，計算完成。

當模型的單元數量較多時，有限元計算量大，計算時間較長，為了提高工作效率，可以采用并行計算方式，在ABAQUS軟件作業管理器中選擇使用多個處理器進行計算。本研究采用雙核處理器進行計算。

1.2.3 后處理部分

打開得到結果的數據文件，通過訪問對象數據庫（objectdatabase，ODB）文件的子對象分析步及增量步，查尋并提取應變能密度數據計算其結果的改變量。將密度添加至結果變量，以場變量的形式輸出。

2 有限元模型

2.1 二維懸臂梁模型

探究初始密度值對骨自優化過程的影響與基于Wolff定律的骨重建研究中均認為二維懸臂梁模型在一定程度上可以模擬長骨結構，利用其受力后密度分布情況來預測骨自優化的最終結構形態是一種可行的方法[20-21]。

本研究選取懸臂梁模型，尺寸參數為長80 mm，寬10 mm，外力載荷取5.0 N的集中力，施加在懸臂梁豎直方向右側中點，并在其左端施加完全約束[20]，二維懸臂梁結構模型如圖2所示。通過與文獻[20-21]實驗結果的對比，以驗證本算法的正確性。

圖2 二維懸臂梁結構模型Fig.2 Two-dimensional cantilever beam structuremodel

2.2 股骨近端模型

對股骨近端區域進行定量計算機斷層掃描（quantitative computerized tomography，QCT），掃描參數為像素值0.937 5 mm，分辨率512×512，層厚2.500 0 mm，電壓80 kV，電流260 mAs，獲取56張股骨近端QCT影像。利用QCT影像在（materialise′s interactivemedical imagecontrol system，MIMICS）軟件中建模，并用MAGICS切取一個股骨冠狀面，將其導入ABAQUS，得到股骨近端有限元模型如圖3所示。

圖3 股骨近端有限元模型Fig.3 Finiteelement model of proximal femur

本研究假定骨組織是各向同性材料，密度與彈性模量之間的關系式為E=3 790ρ3，泊松比為0.3。最大表觀密度ρmax設為1.74 g/cm3，最小表觀密度ρmin設為0.01 g/cm3，所有元素的初始密度值為1.74 g/cm3。分別在股骨關節處及外展肌的附著區域施加4種外力，股骨近端模型載荷條件如表1所示，模型底部所有節點施加完全約束。

表1 股骨近端模型載荷條件Tab.1 Loading conditionsof theproximal femur model

3 結果

3.1 二維懸臂梁模型

懸臂梁模型采用帶縮減積分的四節點平面應力（CPS4R）單元，網格尺寸為1.00 mm，劃分800個單元，進行有限元計算。規定初始密度為1.74 g/cm3，提取密度變量輸出，迭代200次后懸臂梁密度分布結果如圖4所示。

圖4 迭代200次后懸臂梁密度分布結果Fig.4 Density distribution results of cantilever after 200 iterations

從密度分布結果來看，當迭代200次時，沿長軸方向最外側單元密度分布均最高，而對稱軸線兩側向內單元密度按一定比例逐漸降低，懸臂梁被優化成明顯的橋梁工程中常見的桁架結構，與利用ANAYS算法探究初始密度對骨自優化結果的影響和基于Wolff定律的骨重建研究的計算結果一致[20-21]，證明了程序算法的正確性。

3.2 股骨近端模型

二維股骨有限元模型采用CPS4R單元，網格尺寸為2.00 mm，劃分3 492個單元，施加載荷，進行有限元計算。求解過程迭代50次，模擬50天骨重建過程。在每次迭代中計算每個單元的骨組織密度，提取密度數據并得到股骨近端密度分布結果，如圖5所示。可以看出，在股骨表面施加外力載荷組，隨著迭代進行，股骨近端密度分布呈現出3個特征。

圖5 股骨近端密度分布結果Fig.5 Density distribution result of proximal femur

1）外層的股骨干表面骨密度逐漸增強，形成皮質骨區域，最大密度出現在該處。

2）股骨頭及大轉子部位密度減小，形成松質骨區域，密度值在0.442～1.308 g/cm3。

3）股骨干髓腔趨近于0，呈現為“空腔”，Ward三角區也出現了密度最低值，因為該處密度值低，導致出現股骨頸骨折的風險較高。

股骨近端應力分布結果如圖6所示。根據WOLFF定律，骨組織在需要的部位就生長，在不需要的區域就吸收[2]，對比圖5和圖6可以發現，當骨承受較大的載荷時，該區域的應力會較大，骨密度需要增大，反之，應力小的部位，骨密度則較小。

圖6 股骨近端應力分布結果Fig.6 Stressdistribution result of proximal femur

4 討論

本研究利用ABAQUS軟件的二次開發環境，結合現有骨自優化理論，編寫骨程序算法，建立二維懸臂梁模型和股骨近端模型，驗證骨重建程序算法的正確性及準確性。

將初始密度為1.74 g/cm3懸臂梁模型進行200次迭代計算，與宮赫和朱興華[20]研究初始密度值對骨自優化結果的影響、馬宗民等[21]基于WOLFF定律的骨重建研究，所建立懸臂梁模型的計算結果一致，兩者均采用ANSYS軟件進行仿真。從密度分布結果來看，沿長軸方向最外側單元密度分布均最高，沿其軸線兩側向內單元的密度成比例逐漸降低。顯然，這種情況符合骨自優化理論及Wolff定律，試圖用最少的骨量來獲得最大的結構剛度以滿足力學要求，說明本研究編寫的程序算法是正確可靠的。

股骨近端模型的密度分布表明，當關節力和外展肌載荷組施加在股骨上，外力由股骨上端傳遞到股骨干時，股骨干與股骨頭內部的密度大小表現出了明顯差異。股骨干表面逐漸變“硬”，呈現為皮質骨，最大密度主要出現于該處，股骨頭、轉子部位的密度較小，呈現為松質骨，而髓腔內及Ward三角區的骨密度趨近于0，是易引起骨折的脆弱區。所得的密度分布情況，可以表現真實股骨的結構特征，載荷分配較多的區域，需要的骨組織更致密，密度較高，載荷分配較少的區域，用較少的骨量維持結構，說明模擬結果遵循了WOLFF定律。以應變能密度、等效應力作為激勵變量，利用ANSYS軟件數值模擬骨重建過程也得到了與本研究結果相一致的密度分布[22]。結果表明，股骨近端會受所處力學環境的影響，通過骨重建作用，調整、優化其自身結構，證明了所編寫骨重建算法的準確性。

本研究存在一定的局限性。首先是二維模型的局限性，使用二維模型減少了計算成本，但平面模型不能完全地模擬骨組織的真實結構及受力情況。其次，由于實際中骨骼是各向異性材料，且人體真實受力情況十分復雜，有限元分析的工況與真實力學環境存在差異。下一步將把算法拓展，進行三維模型以及不同加載條件下的骨重建研究。但總體上看，股骨近端模型的仿真結果得到的骨組織密度分布情況，與其他學者使用ANSYS軟件的計算結果一致，符合骨組織調節自身結構適應力學環境的規律。

5 結論

綜上所述，本研究利用Python語言對ABAQUS進行二次開發，依據骨自優化理論，以單位質量的應變能密度作為參考變量，建立以密度值變化率為目標函數的程序算法，對模型進行有限元仿真。通過懸臂梁模型計算得到的桁架結構，證明程序算法可以滿足WOLFF定律。股骨近端模型的計算結果能夠反映出股骨內部骨組織的主要結構特征，說明程序算法模擬骨重建過程符合股骨實際情況。希望本研究的方法及結論可以為骨生物力學仿真研究提供新思路。