基于最小規則自組織映射的入侵檢測算法

張亦輝， 劉振棟， 單東方

(1. 山東職業學院 信息中心， 山東濟南250104； 2. 山東建筑大學計算機科學與技術學院， 山東濟南250101；3. 山東財經大學管理科學與工程學院， 山東濟南250014)

網絡帶寬的不斷增加和新型網絡攻擊手段的出現，使得網絡環境愈發不安全，網絡犯罪取證面臨著大型數據集和相關證據提取等多重挑戰，有關學者對此進行了許多研究。文獻[1]中提出網絡取證準備和信息安全框架。文獻[2]中針對不同利益相關者，研究相關網絡取證調查的特征構建問題。文獻[3]中提出了大規模入侵檢測數據集、模糊邏輯(FL)適用性等問題。文獻[4]中的研究結果表明，基于自組織映射(SOM)聚類技術在小樣本數據集上具有非常好的分類效果。軟計算(SC)方法，特別是模糊神經網絡(FNN)[5]，在病毒檢測、木馬入侵防護等方面發揮了很好的作用。 雖然FNN可以從網絡攻擊數據中提取準確分類模型，但是通常需要建立非常復雜的模型，或需要很長時間來推導有效的模型。文獻[6]中指出，FNN包含基于SOM模糊補丁的無監督放置和基于人工神經網絡模糊規則的調整過程2個部分。文獻[7]中強調了SOM的特殊性。文獻[8]中提出一種 SOM圖像分割算法。文獻[9]中使用橢圓區域描述每個SOM節點數據，但沒有給出超偽半徑的定性計算方法，可能導致錯誤，同時，隸屬度函數(MF)的構建也有難度。

鑒于此，本文中針對現有常用算法在大規模數據分析中存在的缺陷進行相應改進，提出基于最小規則自組織映射的入侵檢測算法(簡稱本文算法)，主要改進自動確定SOM的規模，并選取最佳SOM網格和高效的模糊補丁可置信值，從而更好地表征每個群集數據的路徑，以滿足特定標準數字取證，提高入侵檢測的有效性和效率。

1 理論背景

1.1 入侵檢測模型結構

參照文獻[10-11]中的入侵檢測算法，首先進行入侵數據庫的特征選擇，再從選取特征中進行最優特征選擇，利用分類器算法(本文中研究主要集中于分類器設計)，并根據測試集內已知的分類結果進行算法的分類性能驗證和網絡訓練，實現特征集選取的不斷更新，直到算法收斂。入侵檢測模型結構如圖1所示。

圖1 入侵檢測模型結構

1.2 SOM的規模

SOM規模確定是復雜的優化問題，需要采用啟發式算法對數據集分配數據。文獻[12]中利用映射拓撲結構的變化，通過添加新的節點進行迭代優化，直到滿足一定的終止標準。這種方法適用于小型數據集，且無須映射重建，從而降低了計算復雜度。參考文獻[12]，根據Vesanto法給出SOM規模確定的有關定義。

定義1SOM節點的數量為

式中：N為對象的樣本數量；e0、e1分別為樣本集中第一、 第二數據最大特征值。

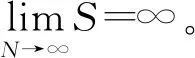
1.3 SOM的結構

SOM聚類輸出可由相近實例表示[13-14]。每個集群將導致與之相應的特定類標簽模糊規則，由于這些都是Mamdani類型的規則，因此，任意的模糊補丁參數πi(i∈{0,1,…,n})表示各樣本特征集a={a0,a1,…,an}的映射。

考慮到補丁區域是一個簡單的矩形，因此可定義對應于特定特征ai空間的長度Lai和中心Cai分別為

參考主成分分析(PCA)方法，樣本集的特征值分解首先要做的是查找最大方差分量。其次，初始特征值是最長分量。這些信息可被用來找出是否需要增加SOM節點數量，來確定樣本覆蓋面大小。

1.4 MF的推導

MF取值區間為[0,1]，用于定義樣品屬于特定規則的程度。三角形MF是常用的函數類型，它的參數很容易從數據中獲得，因此可利用三角形MF來簡化規則的推導。

定義3二維樣本空間具有特定特征的三角形MF形式為

式中：x為樣本集中的任意一點；c為三角形中心；p為基長度。

2 改進SOM網格算法的理論分析

2.1 最佳SOM網格大小

采用皮爾森相關系數r處理最優SOM網格大小確定問題[15]，

引理1[16]在不增加額外記憶功能的前提下分析所得的規則數是有限的。這種約束條件可用來約束SOM大小，從而實現網絡的可理解性，

式中：C為分類問題中的類別數量；M為規則中所有MF的組合數。當Smin=22時，計算結果對應于SOM網絡的最小規模；當Smax=52時，對應于可接受計算復雜度情況下的最大SOM網絡規模。

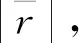
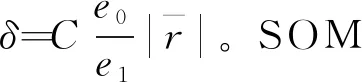
Sb=?Sp/Sa」 ，

式中： ?·」為向下取整函數； 「·?為向上取整函數。

2.2 模糊補丁估計方法

如2.1節中所述，橢圓的補丁配置并未提供橢圓區域完整信息。

定理1實際數據分類橢圓模糊補丁參數πi的估計可重構成參數分布χ2的特定模型擬合問題，利用高斯分布進行擬合。由于這個測試最初是為分類數據設計的，必須使用χ2對方差進行測試，因此在處理真實世界數據時必須進行初步驗證，即

證明：考慮非轉化展開方程，得到方程

樣本數方差S2可視為在特定數據簇中所有元素的方差， 標準偏差σ2作為這個集群的理論偏差， 則通過選取一定的置信區間， 使可置信值β趨近于1， 可得χ2=α2， 因此， 通過引入β， 可實現對數據的控制， 避免數據離群機會。 圖2所示為簡單矩形補丁算法、 普通橢圓補丁算法和本文中算法離散性的差異。

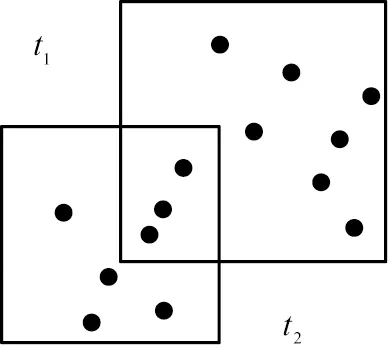
t1、 t2—按簡單矩形補丁算法選取的矩形。

在特定數量規則情況下，應該減少具體算法分類的模糊區域，并減少不確定性重疊區域。綜上所述，可利用χ2查找參數值α2，這里給出的是橢圓補丁參數調整模型。

2.3 相關數據的改進高斯函數

簡單矩形補丁、文獻[7]中普通橢圓補丁不適合改進高斯函數構造，原因是它們不包含構造橢圓模糊補丁的所有可用信息。此外，高斯函數還應依賴于補丁的旋轉和與中心間矩。

定理2在最小組合情況下，用徑向基高斯函數代替三角形MF，為旋轉橢圓模糊補丁規則提供一個更適合的數據擬合。

證明：利用最小原則對旋轉橢圓模糊補丁規則μr進行定義，表示為笛卡爾乘積組合形式

μr=μ0(x)∧μ1(x)∧…∧μN-1(x) 。

利用高斯函數對特征的三角形MF進行替換，μi=siexp{-1/2[(xi-ci)/pi]2}，其中xi為樣本集第i維的任意樣本，ci為第i維的三角形中心，pi為第i維的基長度，尺度因子si∈(0,1]為縮放常數，其他參數是在每個特征空間相應的特性。由此，考慮到不同樣本集合，可對整體的隸屬度進行描述。

μr=s0exp{-1/2[(x0-c0)/σ0]2}∧…∧

sN-1exp{-1/2{(xN-1-cN-1)/σN-1]2}=

其中尺度因子si是未知的。設定si=1，然后利用橢球的廣義方程導出近似高斯函數。

上述過程給出了如何將三角形MF替換為改進的高斯函數，獲得μr。

3 模糊橢圓補丁SOM算法結構

本文中算法主要包含2個過程： 1)利用尺寸參數對SOM初始化，并利用SOM對數據樣本進行分組； 2)模糊規則由模糊聚類的參數提取形成，利用單層人工神經網絡技術調整各模糊規則的權重。參考文獻[17-18]，算法描述如下。

fuzzyPatchesParameters←clustersToRules(clusters-Confing)；

Smin=22,Smax=52,nC←2；

Sopt←Smin+(Smax-Smin)；

retum Hgrid,Wgrid

endfunction

functionclustersToRulesclustersConfig

forallclusters extracted from SOMdo

FuzzyPatchesμ=centroids(cluster)；

FuzzyPatchesμ=(Cov-1)；

endfor

endfunction

functionProposed MF,sample

mahalanobisD←(sample-μ)T

∑-1(sample-μ);

χ2←contingencytable(DF)|φ

ifmahalanobisD≥χ2then

else

endif

returnmf

endfunction

上述算法中，第1行描述了該算法正確運行所必需的初始參數的分配情況，其中φ為橢圓模糊補丁偽半徑，SOMepochs描述了在第1階段SOM訓練代數，NFepochs描述了在第2階段訓練代數，BA為自引導聚合中使用的初始數據集的數據樣本比例。第2行中，OptimalSize用來估計SOM的最佳尺寸，見2.1節中所述。第3行中，SOMtraining為SOM的常規參數訓練。第4行中，clustersToRules將聚類數據轉換成相應的模糊補丁參數，用于形成模糊規則，見2.2節中定理1。

4 實驗

4.1 實驗設置

在算法驗證環節，使用標準的KDD CUP 1999數據集，該數據集具有典型的不平衡特性，是一組網絡入侵實驗數據集。表1所示為KDD CUP 1999攻擊地址。測試集內的數據共有4個不同的攻擊類型數據，即DoS、U2R、R2L、Probe。對于上述攻擊類型，攻擊數據具有不均勻的分布特征，例如在DoS中有的樣本數量非常大，而U2R、R2L和Probe具有的樣本數量較少。

表1 KDD CUP 1999攻擊地址

算法計算平臺名稱為MATLAB 2012a。計算機配置如下：內存容量為8 GB，內存型號為DDR4-2400，處理器型號為i5-7500HQ，操作系統為Windows 7旗艦版。DoS、 U2R、 R2L和Probe這4種不同攻擊類型的訓練樣本數(測試樣本數)分別是8 435(123 166)、 1 126(16 189)、 3 000(4 011)、 52(288)。 測試指標如下。

式中：P為檢測精度；Tp為定性為入侵的行為；Fp為錯誤判定為攻擊的網絡行為。

式中：R為召回率；Tr為定性為正常的網絡行為；Fr為錯誤判定為正常的網絡行為。

式中：W為穩定性；Tn為定性為成功訓練樣本數量；Tm為總訓練樣本數量。

4.2 結果與分析

為了實現對所提算法進行有效性驗證，選取對比算法為普通橢圓補丁算法、決策樹算法、簡單矩形補丁算法。其中，普通橢圓補丁算法和簡單矩形補丁算法均以模糊神經網絡算法為基礎，實驗對比結果如表2所示。

表2 不同算法的實驗結果對比

根據表2中的實驗數據，在DoS類型網絡攻擊中，普通橢圓補丁算法、決策樹算法、簡單矩形補丁算法和本文中算法的檢測精度、召回率以及穩定性指標均可達90%，表明DoS類型的攻擊檢測較簡單，本文中算法優于選取的普通橢圓補丁算法、決策樹算法、簡單矩形補丁算法。召回率、檢測精度和穩定性最差的對比算法集中在R2L、U2R攻擊類型中，只有30%左右，說明用這幾種對比算法檢測攻擊數據的效果很差，但是本文中算法對各類惡意攻擊的檢測率大于70%，表明該算法相對于對比算法具有更好的異常網絡行為攻擊檢測性能。同時，從普通橢圓補丁算法、簡單矩形補丁算法以及本文中算法在上述測試集上的規則數生成數量對比情況看，本文中算法所需的規則數量遠少于普通橢圓補丁算法和簡單矩形補丁算法的，體現了選擇的最小規則方法的有效性。

通過算法測試時間統計可以比較各種算法的計算效率，不同算法的計算效率對比如圖3所示。從圖中可以看出，本文中算法所需要的時間與決策樹算法極為接近，兩者都要少于普通橢圓補丁算法和簡單矩形補丁算法的，體現了本文中算法較高的計算效率。

圖3 不同算法的計算效率對比

5 結語

本文中提出了一種基于最小規則自組織映射橢球模糊補丁投影隸屬度函數的入侵檢測模型算法，給出了基于改進高斯隸屬函數估計的橢圓模糊補丁構造方法，以及相關數據的改進高斯隸屬度函數計算方法，實驗結果驗證了算法的有效性。

下一步研究方向主要包括硬件設備的實現問題、更多入侵數據集的性能測試、算法的并行化計算系統設計。