改進的k最鄰近算法在海量數據挖掘中的應用

黃文秀， 唐超塵， 神顯豪， 周術誠

(1. 福州工商學院工學院， 福建福州350715； 2. 西安電子科技大學通信工程學院， 陜西西安710071；3. 桂林理工大學廣西嵌入式技術與智能系統重點實驗室， 廣西桂林541004；4. 福建農林大學計算機與信息學院, 福建福州350002)

文本分類作為數據挖掘技術的重要環節之一，其分類性能對數據挖掘的效果具有重要影響。特別是對于海量數據挖掘人工整理及分類數據已經不能滿足要求，將海量數據進行有效分類，是數據資源被利用的關鍵，也是數據挖掘需要克服的難題。在數據挖掘研究中，數據文本并非完全獨立存在[1]，利用數據文本間的強聯系性和弱相關性，可以對數據文本進行有效的分類處理，提高了文本管理的有效性。對分類后的數據進行有效處理，能夠更加充分地挖掘出數據內在的價值。

在數據分類過程中， 常用的算法有支持向量機(SVM)、 貝葉斯法及決策樹法等。 文獻[2]中研究了改進的SVM針對樣本不均衡情況下的優化分類方法， 文獻[3]中對改進的貝葉斯方法對文本分類的優化進行了研究。 基于上述3種機器學習挖掘算法的數據分類存在準確度較低的問題， 而k最近鄰(k-nearest neighbor， KNN)算法表現出較強的分類能力， 在數據分類過程中應用非常廣泛[4-5]。 例如， 文獻[6]中提出了一種改進的KNN短文本分類算法， 相比SVM等算法， 該算法的效率提高近50%， 分類的準確性也有一定的提升； 但是， 面對海量數據， 特別是面對處理樣本分布不均衡的大規模數據挖掘任務時， KNN算法的運行效率成為其短板， 并且分類準確度下降[7-8]， 因此如何提高KNN算法的分類效率及分類準確度成為KNN算法研究的關鍵。 本文中采取樣本均衡思想， 根據KNN訓練樣本分布情況， 對樣本的領域密集區域進行優化處理， 旨在進一步提高數據樣本的分類效率和分類準確度。

1 KNN算法

首先假設需要進行分類的2個樣本向量為di、dj(i、j分別為不同的樣本類別)，兩者之間的相似程度計算方法[4]為

(1)

根據式(1)計算的相似度的降序結果進行篩選，選擇前k個樣本作為鄰域。對這k個樣本進行權重設置，設置方法[5]為

(2)

式中：w為樣本的對應權重；Cm為第m類樣本的集合； δ函數為

根據式(2)的計算結果，生成分類決策結果[6]，

(3)

式中Cf為最終分類結果。

2 基于樣本均衡的KNN算法

2.1 樣本均衡原理

假設在KNN算法中存在2個數據樣本A和B。對于僅求兩者交集的情況，若2個樣本的屬性不同，則可能出現A∩B=?。考慮到樣本屬性之間的聯系，若A樣本的第M個屬性和B樣本的第N個屬性存在關聯，那么，從數據挖掘的角度來說A∩B=?并不成立。在實際操作中，KNN算法在解決這種因樣本屬性存在某種或強或弱的關聯(樣本分布不均衡)而引起的分類問題時，會導致KNN算法的性能劣化[7]，運行時間增加，因此必須采用有效方法來優化KNN算法。

2.2 樣本均衡處理

設樣本集合S中2個樣本A、B之間的距離為d(A,B), 那么樣本集合S中的任意樣本A∈S，鄰域ε的圓形區域范圍[8]為

Nε={B|d(A,B)≤ε,B∈D} ，

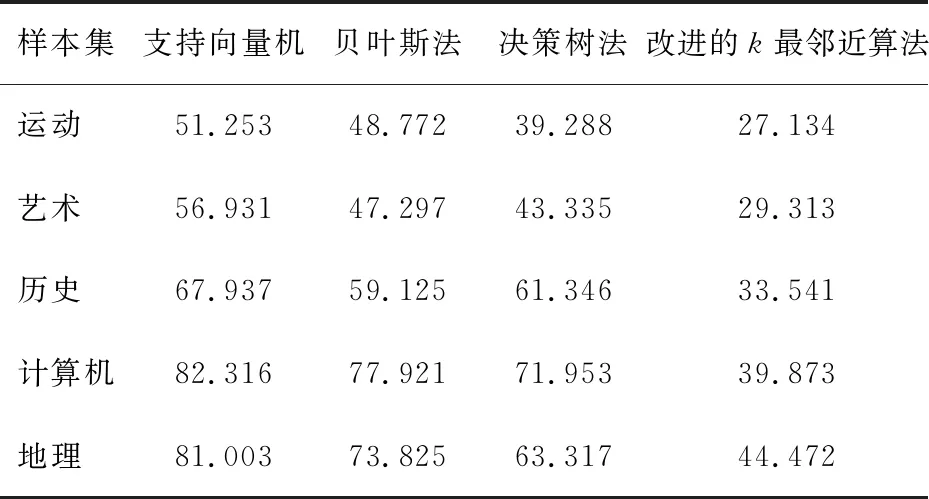
式中D為不同于S的另一個集合。 設樣本A在鄰域ε中的最小樣本個數為Smin， 那么根據Nε與Smin的關系， 可以確定該鄰域內的樣本分布情況[9]， 即當Nε>Smin時，該鄰域為密集區域； 當Nε

圖1所示為文本分布示意圖。 樣本分為“+”和“*” 2類。 從“+”類角度來看， 紅色圈表示“+”類的類內區域， 藍色圈表示“+”類的分界區域。

圖1 文本分布示意圖

文本鄰域的密集區域分布如圖2(a)所示。由圖可以看出，文本B、C均處于密集區域，設文本B的Smin為5，若文本C處于文本B的ε鄰域內，那么將該文本優化掉，同時將Nε縮放，直到Nε=Smin，則文本B的鄰域變為均勻分布區域。經過處理后的文本B的區域如圖2(b)所示。

(a)密集區域分布

對于邊界處的文本處理稍顯復雜，從圖2(a)可以看出，文本A的鄰域內有多個類別，設類別總數為ctot。設邊界區域內的樣本個數為sbor，且有sbor≥Smin。當sbor≤ctot時，邊界區域對每種類別只保留1個樣本[10-11]；當sbor>ctot時，根據每個類別的樣本數量按比例保留各類別樣本。

2.3 基于樣本均衡的KNN算法流程

通過樣本均衡處理后的改進的KNN算法流程如圖3所示。

改進的KNN算法流程有4個初始值需要設定，分別是Smin、ctot、k值和準確度閾值。這4個參數的設置與KNN算法的分類準確度和分類效率有密切的聯系，其中ctot和準確度閾值可以根據實際情況需要設定，一般ctot可根據訓練樣本指定的類別數直接設定[12]，而準確度閾值作為算法迭代運行終止的判別條件，在設置時需要根據實際分類的準確率要求而定。Smin和k值需要在改進的KNN算法模型優化過程中不斷調整來達到理想的分類性能。

3 實例仿真

為了驗證改進的KNN算法在海量數據挖掘的性能，以某圖書館平臺的館藏數據進行實例仿真。選取運動、藝術、歷史、計算機和地理5個類別的樣本，5類樣本的數據樣本集[13-14]如表1所示。

圖3 改進的k最鄰近(KNN)算法流程

表1 5個類別樣本集的屬性參數

3.1 分類準確度

首先，設KNN算法的k值為10，Smin值為5。根據表1，分別對5種不同樣本的ctot進行設定，分別為21、 23、 15、 22、 3，然后分別采用傳統KNN算法和改進的KNN算法對5類不同的數據樣本進行性能仿真，驗證算法的分類準確度，分類準確度指標為查準率和查全率[15]。仿真結果統計如表2所示。

從表2中可以看出，相比于傳統KNN算法，本文中提出的改進KNN算法在分類性能方面表現更優。為了進一步驗證本文中提出的算法在數據挖掘中的效果，在相同數據集情況下，分別采用常見分類算法(SVM、貝葉斯法和決策樹法)進行對比仿真，比較不同分類算法的精準率與召回率的調和平均數F1的最大值、最小值和平均值，結果如表3所示。

表2 傳統k最鄰近(KNN)算法與改進KNN算法的分類準確率

表3 不同分類算法的精準率與召回率的調和平均數F1

與其他3種常見分類算法相比，改進的KNN算法對于5種不同樣本集的F1值更大，表明該算法的分類性能更優。特別是在樣本“計算機”的分類中，F1均值達到0.918 2，比其他算法的均值提升較大。在5種不同類別的數據樣本中，改進的KNN算法的分類性能(按照F1值的平均值從大到小)排序為計算機、 歷史、 地理、 運動、 藝術。

3.2 樣本均衡性能

為了驗證經過樣本均衡處理后的KNN算法的性能，對“運動”樣本集進行訓練，k值設為20，Smin設置為區間[1, 10]，驗證鄰域密集區域的樣本裁剪優化情況，并對樣本均衡處理后的KNN算法的性能和未經過樣本均衡處理的KNN算法性能進行對比，結果如表4所示。

表4 “運動”樣本集裁剪優化結果

通過不斷改變樣本“運動”的鄰域樣本個數最小值Smin，鄰域樣本密集區域不斷改變。當Smin逐漸增大，密集區域的Nε擴大，所需要裁剪優化的樣本數量減少；當Smin較小時，Nε區域很小，因此需要進行大量樣本的裁剪優化，優化比例達到了45.96%。在實際操作中，Smin過小，樣本數量裁剪過多，會影響分類性能，一般優化比例在20%左右較合理。

在實際的改進KNN算法建模過程中，可以通過k值和Smin值組合調節，根據實際需要，設置合適的參數來完成KNN算法的數據分類，以便能夠提高改進KNN算法的分類準確度。

3.3 運行時間

KNN算法k值設為10，Smin設為8，對5種不同的樣本集進行分類，對3種常見分類算法與改進的KNN算法的運行時間進行仿真，要求F1值不小于70%，否則算法繼續，直到F1值大于或等于70%。不同分類算法的運行時間如表5所示。

表5 不同分類算法的運行時間 s

在實驗數據集相同的條件下，設置F1值大于或等于70%為閾值，當達到該條件時，改進的KNN算法優勢明顯，所用的時間比其他3種算法所用的時間更少。

不斷提高F1值的閾值門檻，繼續實驗，所有算法的運算時間均在增加。當閾值門檻提高至80%時，在對樣本“藝術”進行分類時，發現SVM算法并未收斂，這可能是由SVM對樣本“藝術”分類準確度較低導致的。綜合而言，改進的KNN算法在分類準確度和分類時間方面更有優勢。

4 結語

將KNN算法的訓練樣本經過樣本均衡策略處理后，能夠較大幅度地提高樣本分類準確度和分類效率。與傳統KNN算法及常見分類算法相比，改進的KNN算法表現出更穩定的F1指標性能和運行時間性能，但是，對于高維稀疏數據，該算法的運行效率下降較明顯。后續將對如何將KNN算法與降維方法和特征選擇方法進行結合開展進一步研究。