關于Philon線的拓展研究①
于學明 李世臣
(1.河南省商水縣希望中學 466100;2.河南省周口市川匯區教研室 466001)
文[1]介紹了Philon線的定義及其性質,揭示了在定角內過定點的直線,被角所截最小線段的幾何特征.由于過定點的直線可以看作是以定點為頂點的平角,于是我們把平角換成某個定角θ(0°<θ<180°)進行了探究,發現存在類似的Philon線,同樣具有優美的幾何性質,最后以幾何視角詮釋了圓錐曲線夾在兩條固定切線間切線段長的極值問題.
廣義Philon線定義如圖1,已知∠MON是定角,點P是角內的一個定點,點A,B分別在射線OM,ON上,∠APB的大小為定值,當線段AB的長度取得極值時,我們稱此時的線段是在定角內,以定點為頂點,張角為定值的廣義Philon線.

圖1
下面探討廣義Philon線的幾何特征.
定理如圖2,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.連接OP,若∠AOP=α,∠POB=β,∠BPA=θ,∠PAO=x,∠OBP=y,則

圖2

證明設PO=ρ,在△OAP和△OPB中,
由正弦定理得
在△APB中,由余弦定理得
AB2=PA2+PB2-2PA·PB·cosθ
因為α+β+x+θ+y=360°,
所以y=360°-(α+β+θ+x).

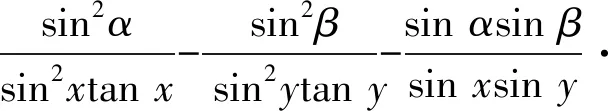
移項整理得
提取公因式后即得(※)式.證畢.

性質1如圖3,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.作AD⊥PB于點D,BE⊥PA于點E,直線OA,OB過點A,B的垂線分別交直線BE,AD于點F,G,連接PF,PG,則S△PAF=S△PBG.

圖3
證明如圖2,在△OAP和△OPB中,由正弦定理知
代入(※)式得
因為AD⊥PB,BE⊥PA,
則AE=PA-PB·cosθ,
BD=PB-PA·cosθ.
因為AF⊥OA,BG⊥OB,
則∠PAF=x-90°,∠GBP=y-90°,

于是PA·EF=PB·DG,


性質2如圖4,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.直線OA,OB過點A,B的垂線交于點H,則△PAB的外心S在直線PH上.

圖4
證明設直線AH,BH,PH分別交PB,PA,AB于點J,I,K,作AD⊥PB于點D,交直線BI于點G,作BE⊥PA于點E,交直線AJ于點F,設直線PH交AB于點K.
對于直線BI截△PAD,直線AJ截△PBE,由梅涅勞斯(Menelaus)定理得
由于AP·FE=PB·DG,

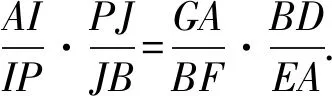
對共點于H的三條直線,
由塞瓦(Ceva)定理得
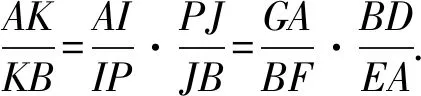
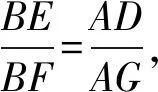
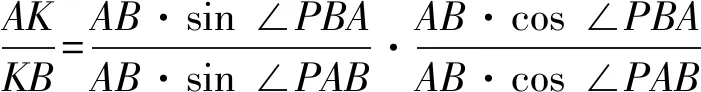
設點K到AP,BP的距離為dK-AP,dK-BP,則
設△PAB的外接圓半徑為R,S到PA,PB的距離為dS-AP,dS-BP,則

所以△PAB的外心S在直線PH上.
性質3如圖5,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.HA⊥OM,HB⊥ON,HC⊥PA于點C,HD⊥PB于點D,則CD∥AB.
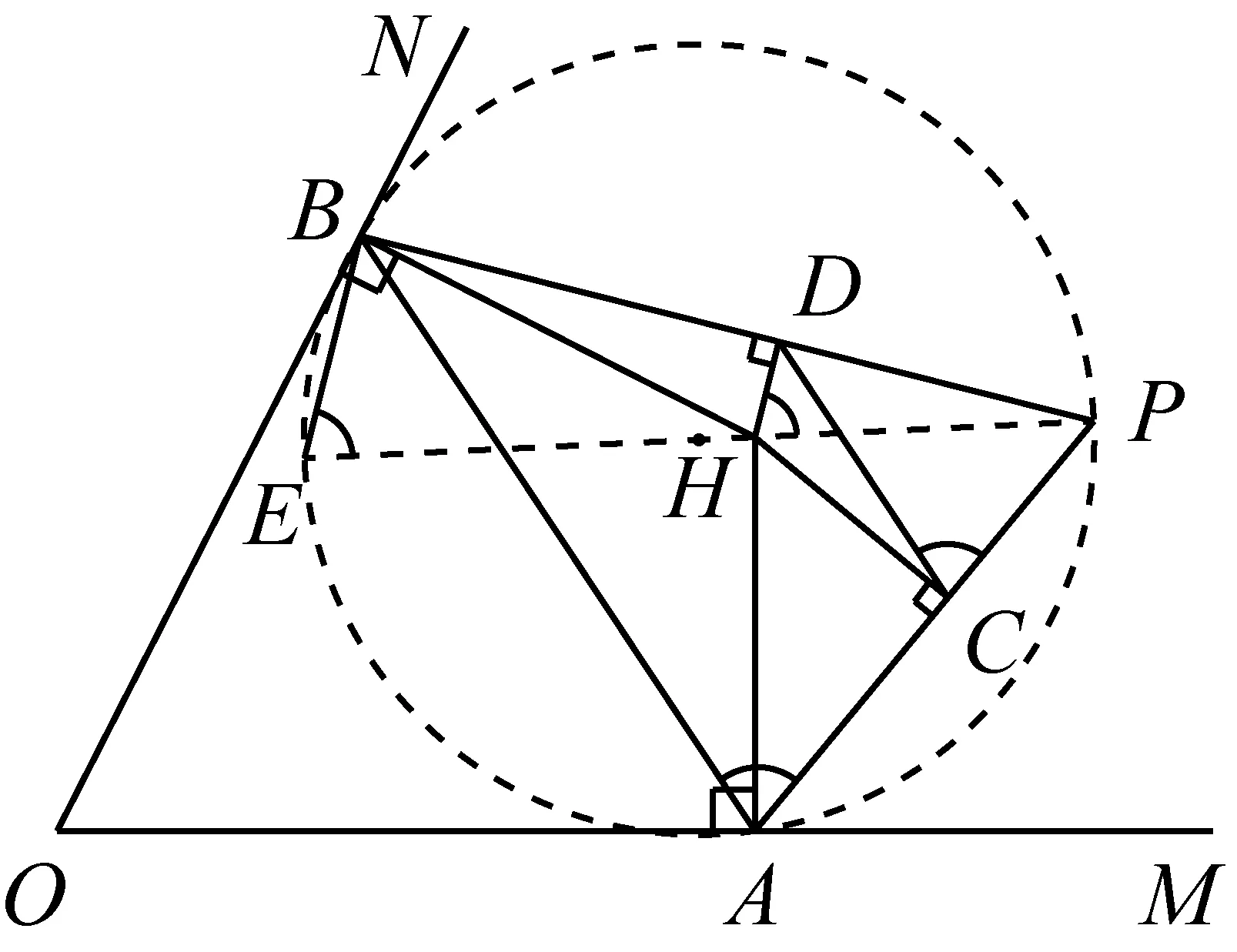
圖5
證明設直線PH與△PAB的外接圓另交于點E.
由性質2知,線段PE是△PAB的外接圓直徑.
連接BE,則∠BEP=∠BAP,BE⊥BP.
因為HD⊥BP,則BE∥HD,
所以∠BEP=∠DHP.
因為HC⊥PA,HD⊥PB,
所以H,C,P,D四點共圓.
所以∠DHP=∠DCP.
于是∠BAP=∠DCP,所以CD∥AB.
為了以下證明方便引入兩個引理.
引理1如圖6,線段AB,CD交于點O,△OAC,△OBD的外接圓交于點P,PE⊥AC于點E,PF⊥BD于點F,PG⊥AB于點G,PH⊥CD于點H,連接PA,PB,PC,PD,EF,GH,求證:(1)E,F,G,H四點共線;(2) △PAB∽△PEF∽△PCD;(3) △PAC∽△PGH∽△PBD.
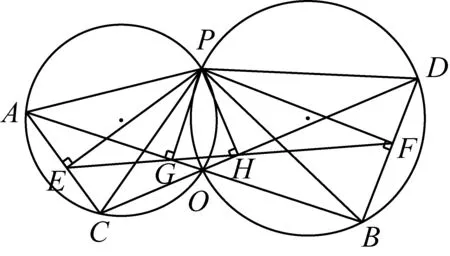
圖6
證明(1)因為PE⊥AC,PF⊥BD,PG⊥AB,PH⊥CD,由西姆松定理知,點E,G,H共線,點G,H,F共線.所以E,G,H,F四點共線.
(2)由P,A,E,G;P,E,C,H四點共圓,
所以∠PAG=∠PEG=∠PCH.
同理∠PBO=∠PFH=∠PDH.
所以△PAB∽△PEF∽△PCD.
(3)由P,A,E,G;P,G,B,F四點共圓,
所以∠PAC=∠PGH=∠PBD.
同理∠PCA=∠PHG=∠PDB.
所以△PAC∽△PGH∽△PBD.
引理2如圖7,點P是△ABC外接圓上一點,連接PA,點P關于△ABC的西姆松線是l,AG⊥l,則∠PAB=∠CAG.

圖7
證明設l與AB,AC分別交于點D,E,連接PD,PE.
因為l是點P關于△ABC的西姆松線,所以PD⊥AB,PE⊥AC.所以A,D,P,E四點共圓,∠PAB=∠PED.
因為PE⊥AC,AG⊥l,
所以∠PED=∠CAG.
所以∠PAB=∠CAG.
性質4如圖8,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.直線OA,OB過點A,B的垂線交點為H,過A,H,P三點的圓與直線PB交于點C,直線AC交過B,H,C三點的圓于點Q,PD⊥AB于點D,QE⊥AB于點E,則AD=BE.
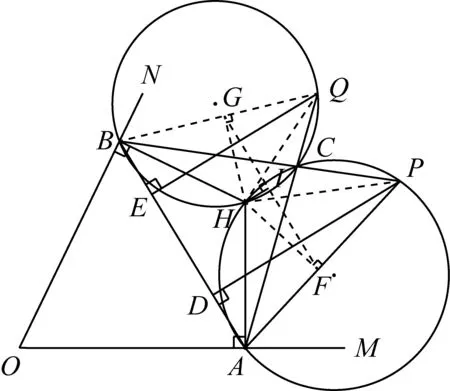
圖8
證明連接BQ,HQ,HP,
由引理1(3)知△HAP∽△HQB.
作HF⊥AP于點F,HG⊥BQ于點G.

連接GF,由引理1(1)知,直線GF是點H關于△APC和△BCQ的西姆松線.
由性質3知,GF∥AB.
因為PD⊥AB,QE⊥AB,
所以PD⊥GF,QE⊥GF.
由引理2知∠APD=∠HPC,∠BQE=∠HQC.
作HI⊥GF于點I,由引理1(2)知
∠HFI=∠HPC,∠HGI=∠HQC.
所以∠APD=∠HFI,∠BQE=∠HGI.
所以Rt△APD∽Rt△HFI,
Rt△BQE∽Rt△HGI.

所以AD=BE.
性質5如圖9,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.直線OA,OB過點A,B的垂線交點為H,過A,H,P三點的圓與直線PB交于點C,直線AC交過B,H,C三點的圓于點Q,直線PH交△PAB的外接圓于點J,則JQ⊥AB.

圖9
證明作PD⊥AB于點D,QE1⊥AB于點E1,由性質4知,AD=BE1.
作JE2⊥AB于點E2,
由性質2知,PJ是△PAB的外接圓直徑.
所以AD=BE2.
于是BE1=BE2,點E1,E2重合.
所以JQ⊥AB.
性質6如圖10,在定角∠MON內,線段AB是以定點P為頂點,張角為定值的廣義Philon線.直線OA,OB過點A,B的垂線交點為H,HT⊥AB于點T,過A,H,P三點的圓與直線PB交于點C,直線AC交過B,H,C三點的圓于點Q,則∠PTH=∠QTH.

圖10
證明作直線PH交△PAB的外接圓于點J,由性質5得JQ⊥AB于點E.
連接JB,則JB⊥BP.作HK⊥BP于點K,

作PD⊥AB于點D,由性質4,AD=BE.
性質4已證∠APD=∠HPK,
∠BQE=∠HQC=∠HBK.
所以,Rt△APD∽Rt△HPK,
Rt△BQE∽Rt△HBK.


因為HT⊥AB于點T,所以PD∥HT∥JE.


所以Rt△PDT∽Rt△QET.
于是∠PTD=∠QTE.
所以∠PTH=∠QTH.證畢.
以上探究了廣義Philon線的性質1~6,下面探究其與圓錐曲線的關系.
由文[2]知道:“在橢圓中,一條切線介于兩條定切線間的部分,在一個焦點的視角為常量.”逆向思考:一條動直線被兩條固定直線所截,所得線段對一個定點的視角為常量,這些動直線的包絡是否是一條以定點為焦點的圓錐曲線呢?這一猜想很容易在動態數學軟件Geogebra上進行驗證,下面僅給出橢圓情形的證明過程.
命題如圖11,已知兩條定直線的交角∠MON=ω,動直線l交定直線于點Y,Z,線段YZ與定點P的視角∠YPZ=θ為定角.若ω+θ<180°,則l的包絡曲線是橢圓.

圖11
證明作PD⊥l于點D,PU⊥OM于點U,PV⊥ON于點V,因為ω+θ<180°,則點P在△OYZ的外接圓外部.
由西姆松(Simson)定理知,U,D,V三點不共線.連接DU,DV,由于P,U,Y,D;P,V,Z,D四點共圓,易知∠DPY=∠DUY,∠DPZ=∠DVZ.
在凹四邊形OUDV中,∠UDV=∠UOV+∠DUO+∠DVO=∠UOV+∠DPY+∠DPZ=∠MON+∠YPZ=ω+θ.
由條件知U,V是定點,點D是動點,∠UDV是定值,所以D,U,V三點確定一個定圓.設圓心為W,半徑WD為a.延長PW至Q,使WQ=PW;延長PD至X,使DX=PD.連接QX,交直線l于點T,則XQ=2WD=2a.連接TP,易知TP=TX,所以TP+TQ=QX=2a(定值).
由橢圓及其切線的定義知,點T的軌跡是一個橢圓,直線l切橢圓于點T.所以l的包絡曲線是橢圓.證畢.
根據廣義Philon線的定義和性質判斷,在橢圓中,介于兩條定切線之間,且取得極值的切線段就是廣義Philon線.焦點在這條切線上的射影到切線段端點的距離相等.這樣,用廣義Philon線直觀地解釋了圓錐曲線夾在兩條固定切線之間切線段長的極值問題.對于拋物線(ω+θ=180°)和雙曲線(ω+θ>180°)兩種情形可作類似的解釋.
本文探討了廣義Philon線的幾何特征,關于怎樣用已知量來表達極值,以及取得的極值是極大值還是極小值問題有待進一步研究.

