涉及三角形中兩角差正割的不等式

王 文 陳亞平

(1.合肥師范學院數學與統計學院，中學數學教學編輯部 230601；2.安徽省合肥市南門小學上城國際分校 230061)

三角形ABC中，R,r分別為外接圓半徑和內切圓半徑，匡繼昌在文[1,P262.173]收錄了尹華炎和張小明的一個結果如下:

但沒有下界估計，我們得到如下一個極為對稱的上下界估計.

定理在三角形ABC中，R,r分別為外接圓半徑和內切圓半徑，則有

等號成立當且僅當三角形為等邊三角形.

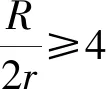
(2)此不等式也可看成Euler不等式的一個隔離.

證明由積化和差公式和正弦定理可得

(1)

應用算術幾何平均不等式

由Cauchy不等式

及公式a+b+c=2p，abc=4Rrp，

(2)

并應用文獻[1,P240, 11]中

則

(3)

從證明過程中每個不等號成立的條件可知等號成立當且僅當三角形是等邊三角形.

下面證明左端成立.

由式(1)應用算數幾何平均不等式可得

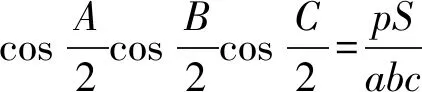
(4)

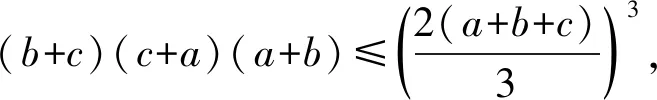
所以

(5)

從證明過程中每個不等號成立的條件可知等號成立當且僅當三角形是等邊三角形.再由(3)和(5)即得結論成立.