小議向量背景下高考立體幾何大題載體模型建系
凡森泉
摘要:以近些年高考改革的實際現狀作為切入點,綜合中學向量以及立體幾何這兩種教學體系之間的聯系進行分析。建立在高考試題的基礎上,針對幾何圖形進行歸類,總結具體的空間直角坐標系的建立方法,確保能夠為相關教學體系改革以及研究提供參考依據。
關鍵詞:向量;立體幾何;載體模型
一、基礎分析背景
綜合空間向量的知識體系來講,空間向量本身具有一定的代數形式和幾何形式,這種雙重性進一步增加了空間向量在多種知識點中的應用價值。它建立在數形結合的基礎上,打造了新的數學解題和思考工具,能夠以結合已知條件構建坐標系,通過向量本身的性質以及運算邏輯,提供更為明確且簡單的證明方法[1]。因此空間向量在融入了數學教材之后,在解決立體幾何位置關系以及其他問題時有一定的促進作用,并且這種解題方式也寫入了高考中。
綜合實際的應用情況來看,空間向量在立體幾何解題過程中,常用的方式以幾何推理和向量解法為主,而近些年的高考中也存在大量的典型習題,能夠為后續空間直角坐標系的建立方法提供清晰明確的指引。
二、基礎原理簡述
建立空間直角坐標系的核心依據便是實現空間向量基本定理與空間圖形的融合。我們假設存在這樣一組不共面:,那么針對任意一個空間向量都存在著唯一的一對有序實數組(x,y,z),促使。
而綜合具體的邏輯分析來看,如果將其中三個基向量轉化成可以兩兩相互垂直的三個單位向量,那么既有的有序實數組(x,y,z)就可以稱之為向量在空間直角坐標系中的具體坐標,這一理論在當前的諸多習題中,我們都可以以這種邏輯思維方式進行思考,這樣能夠有效解決部分復雜的幾何問題。
三、基于高考題型的空間向量建系邏輯
(一)常見的規則幾何體和建系邏輯
常見的規則幾何體主要以正方體、長方體以及各類型棱柱為主,在當前的高考中頻繁出現,并且成為了最基礎的幾何圖形解題類型,以下選擇長方體作為主要的題型進行代表性分析。
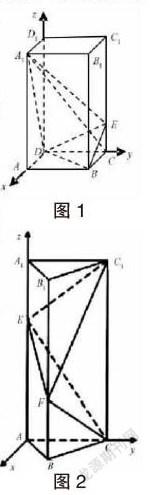
(1)正四棱柱
從實際的建系角度來講,可以利用同一頂點處的三條棱兩兩相互垂直的原理進行思考,另外邊長相等以及倍數關系也可以作為建系的主要參考依據[2]。
例題1:存在一個正四棱柱ABCD—A1B1C1D1,其中AA1=2AB=4,點E在CC1上,并且C1E=3EC。見圖1。求證:A1C垂直平面bEd(垂直嗎?),求二面角A1-DE-B的大小。
(2)三棱柱相關習題
從解題角度分析,可以直接建立在直棱柱側棱與底面面垂直關系以及底面三角形中的線的垂直特性角度進行計算。
例題2:在2011年的湖北卷高考習題中,已知正三棱柱ABC-A1B1C1的底面邊長均為2,則側棱的長度為,側棱AA1上有一點E,BB1上有一點F,且AE=,BF=。如圖2。求證CF垂直于C1E,求二面角E-CF-C1的大小。
(二)不規則幾何體及其建系規則
結合不規則幾何體的實際情況來看,與規則幾何體之間的主要差異便是需要學生具備較強的空間邏輯思維,能夠將平面上的習題已知條件轉化為立體空間中的關系,這樣才能夠實現知識邏輯關系的定位。
(1)折疊問題
首先,針對折疊問題進行分析,其中邊和角存在變與不變的特點,定位這些特殊的關系,最后能夠得出較為明顯的相互垂直的線[3],這樣可以實現快速的建系。
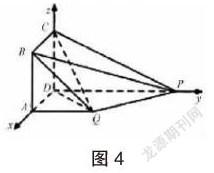
例題4:在梯形ABCd中上下底邊分別為2和6,高為,沿著對稱軸OO1進行折疊,折成直二面角。如圖4所示。求證AC垂直于BO1,求二面角O-AC-O1的大小。
(2)非規則幾何體的實際分析以及建系
首先從空間向量的角度進行分析,若圖中未能提供具有已知條件的兩兩相互垂直的直線,那么首先應該找到一個線面的垂直關系,然后在這個垂直關系中找到經過垂足的兩條相互垂直的直線,同時還要考慮到合理建系的實際規則,即促使相關點的坐標可以在整個坐標中凸顯出來,且形式較為簡單,這樣能夠有效減少計算量。
例題5:已知ABCD為正方形,其中PD垂直于平面ABCD,且PD平行于QA,QA=AB=1/2PD。如圖5所示。求證,PQC垂直于平面DCQ,同時求二面角Q-B-PC的余弦值。
結束語:
結合近幾年的新課程高考考題來看,幾何問題的解析可以直接通過向量問題來進行優化,其中不僅可以簡化思考邏輯,也能夠進一步實現多種知識點之間的相互轉換,對于強化學生的綜合能力有一定的促進作用,同時也可以為未來的課程優化以及教學體系創新提供有效的參考依據。
參考文獻:
[1]齊鵬飛.借力空間向量法巧解立體幾何軌跡問題[J].理科考試研究,2021,28(21):13-16.
[2]董軍浪.幾何點及其坐標/向量的規范表達[J].西安工業大學學報,2021,41(05):514.
[3]王春芳.例談立體幾何四面體中關于“棱”的問題[J].中學生理科應試,2021(10):13-15.

