航天員虛擬訓練中的一維直線運動速度規劃算法
王 嵐,林凌杰,常 影,薛 峰
(哈爾濱工程大學機電工程學院,哈爾濱 150001)
0 引 言
航天員在太空中進行任務時,感受不到重力的存在,但慣性力依然存在[1-2]。如果物體的質量較大,則航天員很難保證其在目標點的速度為零。在作業過程中,較大的慣性力可能會使航天服手套撕裂,因此有必要在地面對航天員進行模擬訓練。
本文在文獻[1]所研究的基于虛擬現實技術的航天員作業訓練環境下,在航天員完成搬運或安裝某一目標物體的過程中,對目標物體的速度進行規劃。從而對航天員進行有效的示教,提高航天員的訓練速度,同時可以為航天員作業訓練系統的模擬仿真和建立“虛擬人”模擬仿真系統提供參考。
速度規劃算法種類繁多,最常使用的是直線型加減速控制算法、S型曲線加減速控制算法等。直線型加減速算法是最簡單易行的算法,但其加速度存在突變點,導致沖擊較大[3]。S型曲線保證了速度和加速度的連續,沖擊較小。文獻[4-6]中的方法均假設允許的最大速度和最大加速度為常量,通過相平面法,得到各階段的運行時間的解析解。
近年來,直接方法成為時間最優速度規劃的研究重點,該方法通過將時間連續模型離散化,將時間最優速度規劃轉化為一個靜態最優化問題,得到時間最優速度規劃的數值解[7]。楊亮亮等[8]將關于加速度變化時間的方程組化簡為一元高次方程后,轉化為單一凸型函數,進而用牛頓迭代法進行求解。Lin[9]提出了一種基于最小加加速度的關節機器人軌跡規劃算法,該算法將軌跡離散化之后,采用粒子群算法和K-means聚類,求出各段軌跡所需要的時間,但每段軌跡內的加加速度均包含t-3項,當t過小或軌跡分段的數量較多時,迭代后的加加速度不易收斂,降低算法的穩定性。文獻[10]和文獻[11]分別提出了基于遺傳算法和粒子群算法的速度規劃算法,將最大加速度和最大速度簡化為常量。Liang等[12]采用迭代的方式,從零開始逐步提高B樣條曲線的各個控制點,直至逼近約束條件。Yuan等[13]提出了一種新型的前向和后向檢查算法,通過多個解析方程,直接求出各節點的最優解。以上算法均假設在進行速度規劃之前,待規劃點的加速度約束為已知量或常量,而對于本文來說,只有對速度進行規劃之后,才能獲得加速度約束。
Bharathi等[14]將軌跡離散化之后,在每個節點處求出允許的最大速度,實現了高階動態約束,但其算法在每個節點處都通過二分法求解,增加了求解時間。由于所研究的對象不同,上述算法均無法直接應用于本文所研究的問題中,目前還沒有一種考慮人體生物力學模型的速度規劃算法。
本文從運動生物力學的角度出發,建立了手臂的動力學模型及肘關節的骨骼肌模型,分析了航天員搬運物體的不同情況,并對肌肉激活度進行規劃。通過粒子群算法求解出各個階段的時間,實現了目標物體的時間最優速度規劃。
1 人體上肢生物力學模型
1.1 人體上肢動力學模型
在太空中,航天員在搬運質量非常大的物體時,會在反作用力的作用下產生運動。最好的搬運方法就是讓物體在航天員的矢狀面內做一維直線運動,此時航天員只會發生前后的平移,而不會發生旋轉,容易控制住自己的身體。航天員通過調整位置,將復雜的搬運作業分解為若干個矢狀面內垂直于冠狀面的一維直線運動。因此,文獻[1]和文獻[15]均將航天員運送物體的作業訓練視為在水平面內做臥推運動,建立推拉物體模型如圖1所示。圖中,l5和l1分別表示左、右上臂的長度,l4和l2表示分別表示左、右前臂的長度,l6表示兩個肩關節之間的距離,l3表示左右兩手之間的直線距離。m1,m2,m4,m5分別表示四肢的質量,M代表目標物體的質量,T1,T2,T5,T6分別表示右肩關節、右肘關節、左肘關節、左肩關節產生的力矩,θ1表示肩關節角度,θ2表示肘關節角度。lp表示人體腕關節和肩關節在冠狀面上的投影之間的距離,F′l和Fl分別為左右兩臂承受的物體的慣性力。
取θ1,θ2為廣義坐標,T1,T2為廣義力,對右臂列拉格朗日動力學方程[16]可求得
Fl[l1cosθ1+l2cos(θ1+θ2)]
(1)
(2)
式中:
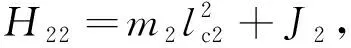
h112=h122=-h221=-m2l1lc2sinθ2。
其中,lc1,lc2分別為上臂的質心到肩關節的距離和前臂的質心到肘關節的距離,J1,J2分別為上臂和前臂的轉動慣量。
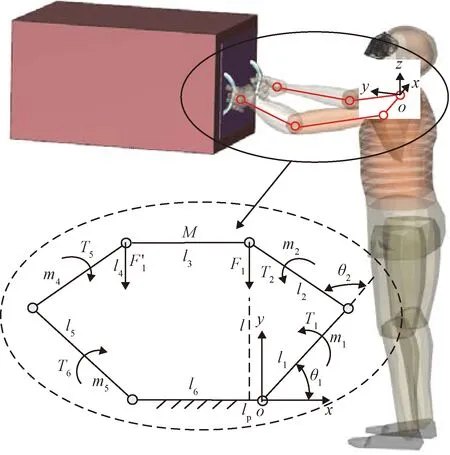
圖1 推拉物體模型Fig.1 Push-pull object model
如果物體只做矢狀面內垂直于冠狀面的一維直線運動,則左臂和右臂承受的慣性力相同,可求得
(3)
式中:M為物體的質量,a為物體的加速度。
人體腕關節和肩關節在冠狀面上的投影之間的距離
(4)
將式(3)、式(4)分別代入式(1)和式(2)中可求得由肩關節和肘關節決定的物體最大加速度的絕對值分別為
(5)
(6)
物體的最大加速度
amax=min(a1max,a2max,aglove)
(7)
式中:aglove是航天服手套被撕裂的加速度。
與物體的質量相比,關節的角速度、角加速度、人體上臂的質量、轉動慣量都很小,對式(5)和式(6)的影響非常小。因此,a1max和a2max的大小主要取決于|lp|和|l2cos(θ1+θ2)|的大小。圖2表示出了右臂可能的三種位姿。由于航天服的限制,取θ1的范圍為[30°,75°],取θ2的范圍為[10°,120°]。
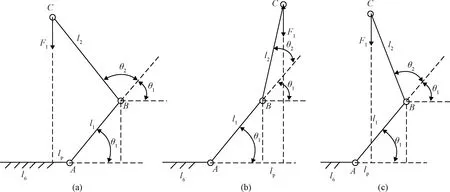
圖2 右臂存在的三種位姿Fig.2 Three postures of the right arm
當點C在冠狀面的投影位于A點以左,由于θ1小于90°,因此在整個運動過程中,航天員的右臂只存在圖2(a)一種情況,此時,由圖中可以看出,lp≤0時,l2cos(θ1+θ2)<0,且|lp|一定小于|l2cos(θ1+θ2)|。
當點C在冠狀面的投影位于A點右側時,可能會出現圖2(b)和圖2(c)兩種情況。如果在θ1取最小值時,點C在冠狀面的投影也位于B點以右,那么在整個運動過程中,點C在冠狀面的投影始終位于B點以右,即始終是圖2(b)中的情況。此時,θ1+θ2<90°,l2cos(θ1+θ2)>0,|lp|一定大于|l2cos(θ1+θ2)|。此種情況出現的條件為lp>l1cosθ1 min,取l1=280mm,可求得lp>242.5mm。
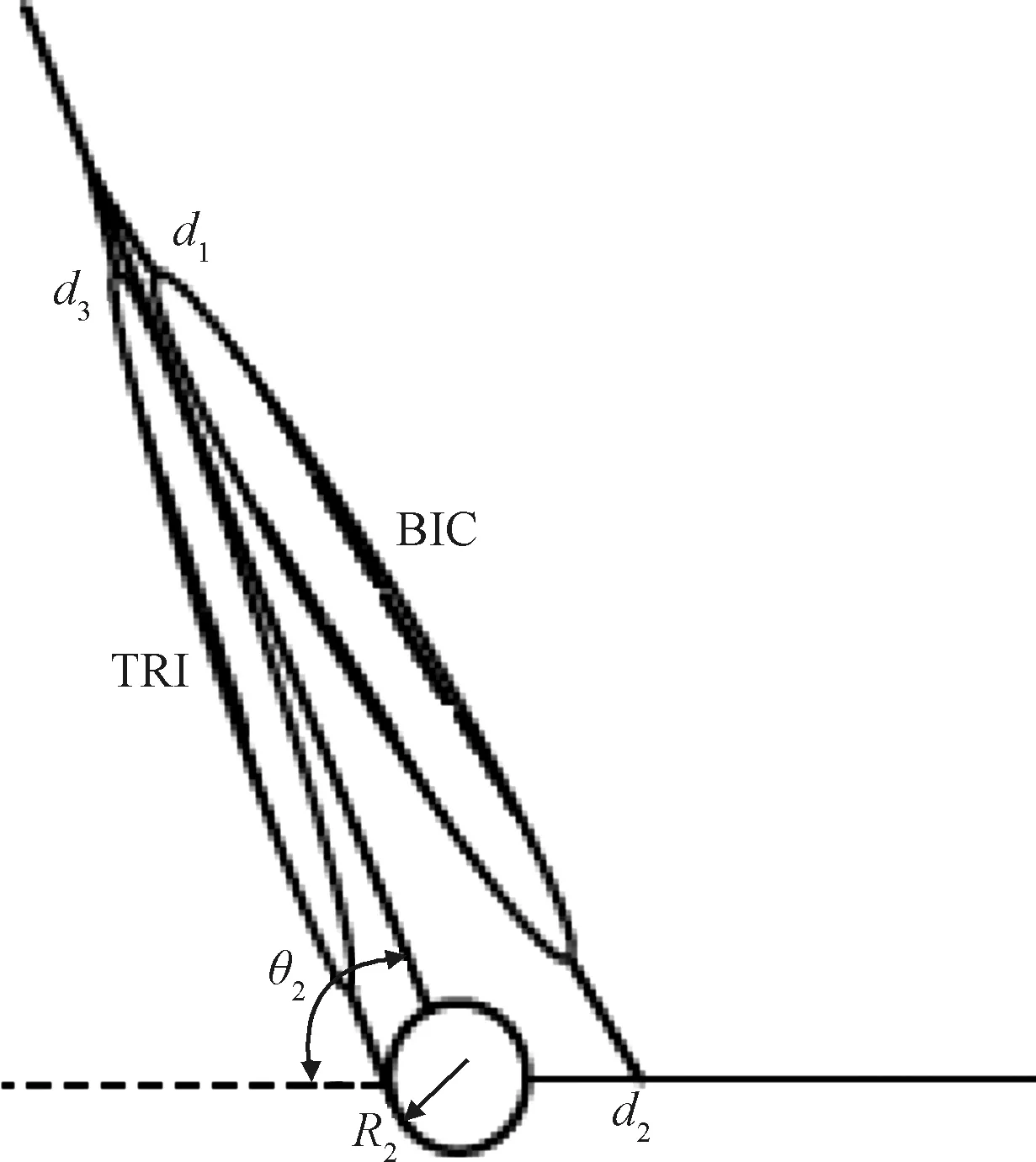
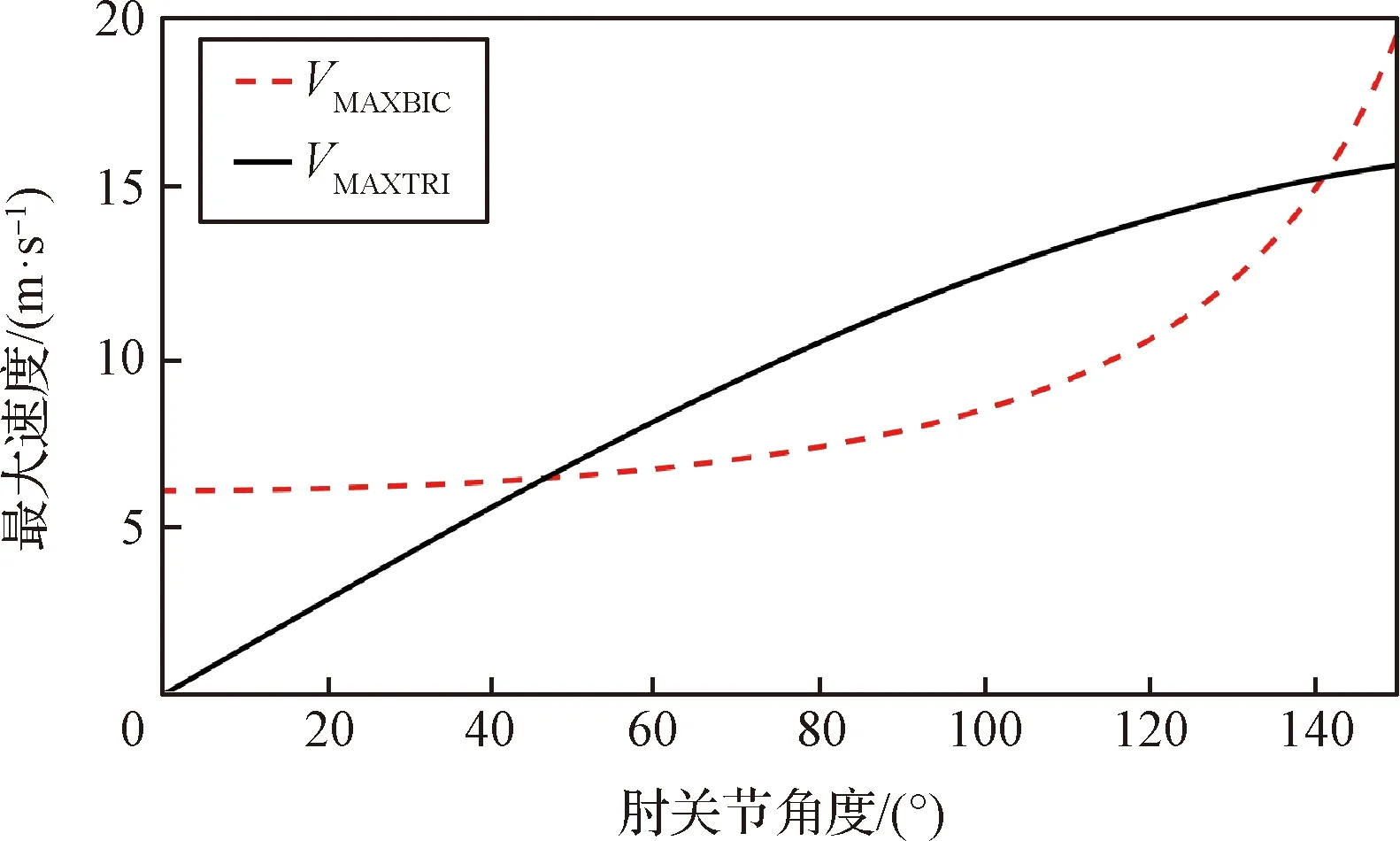
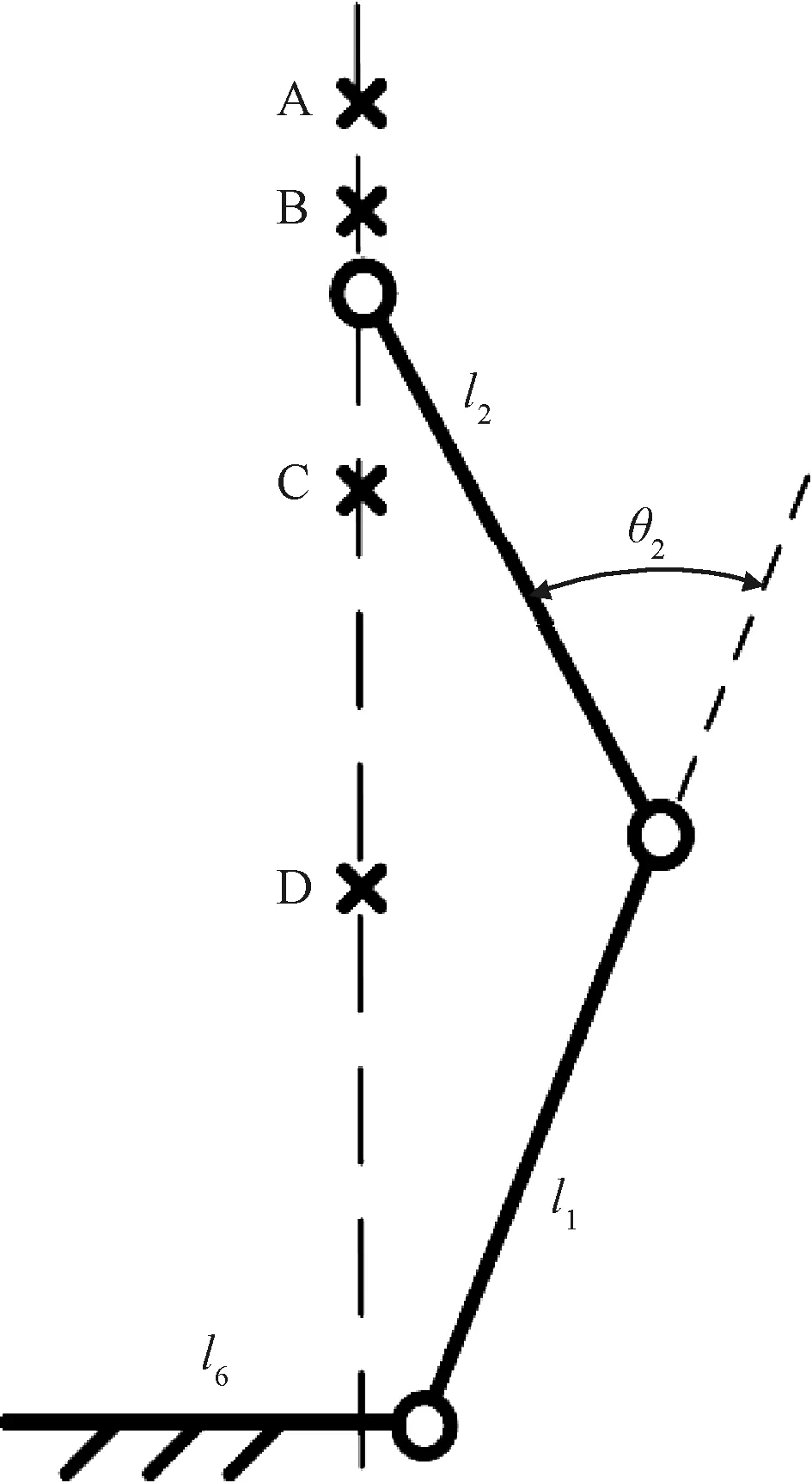
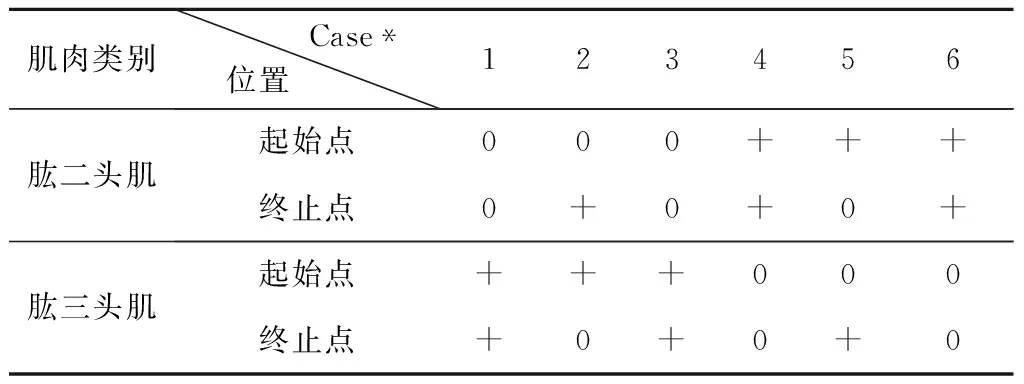
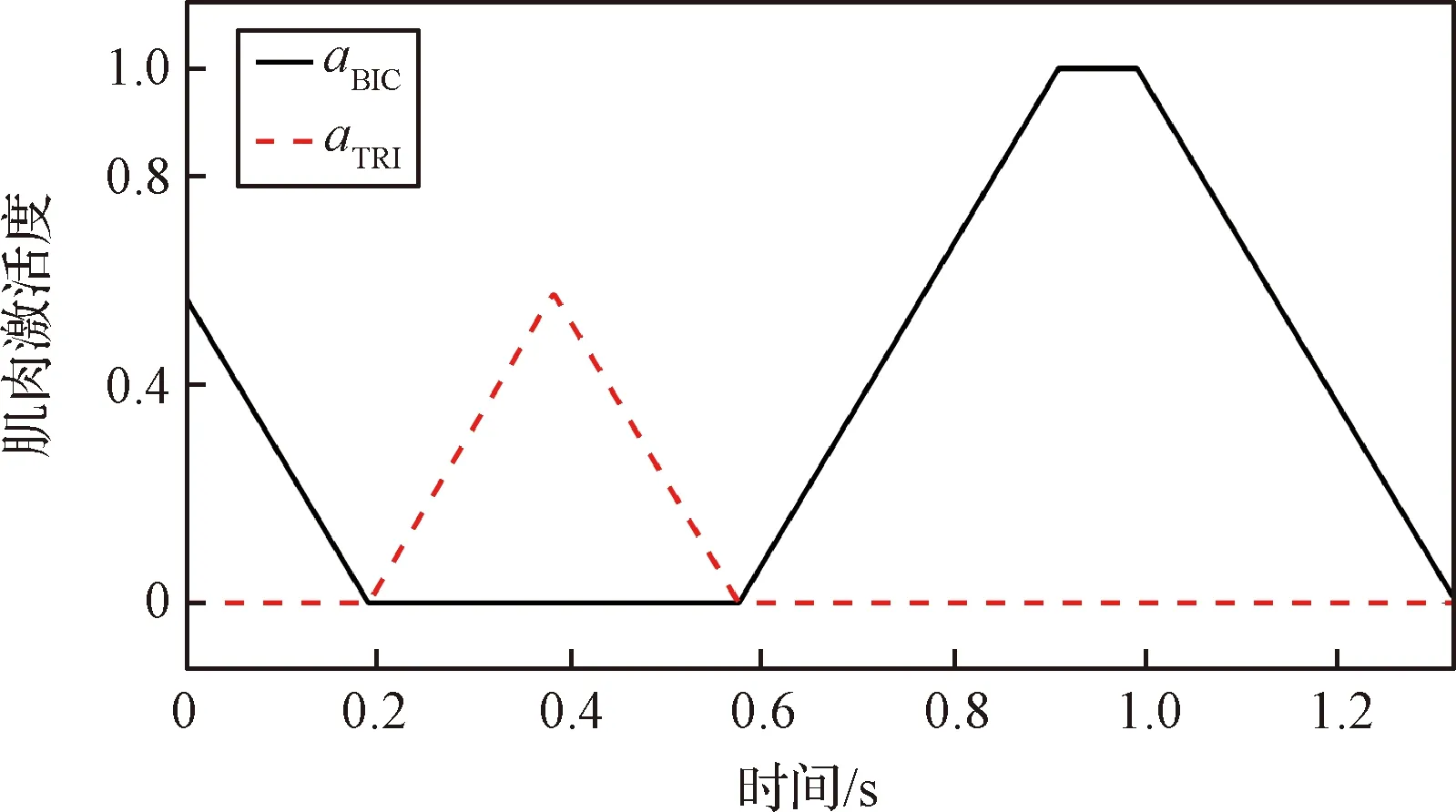
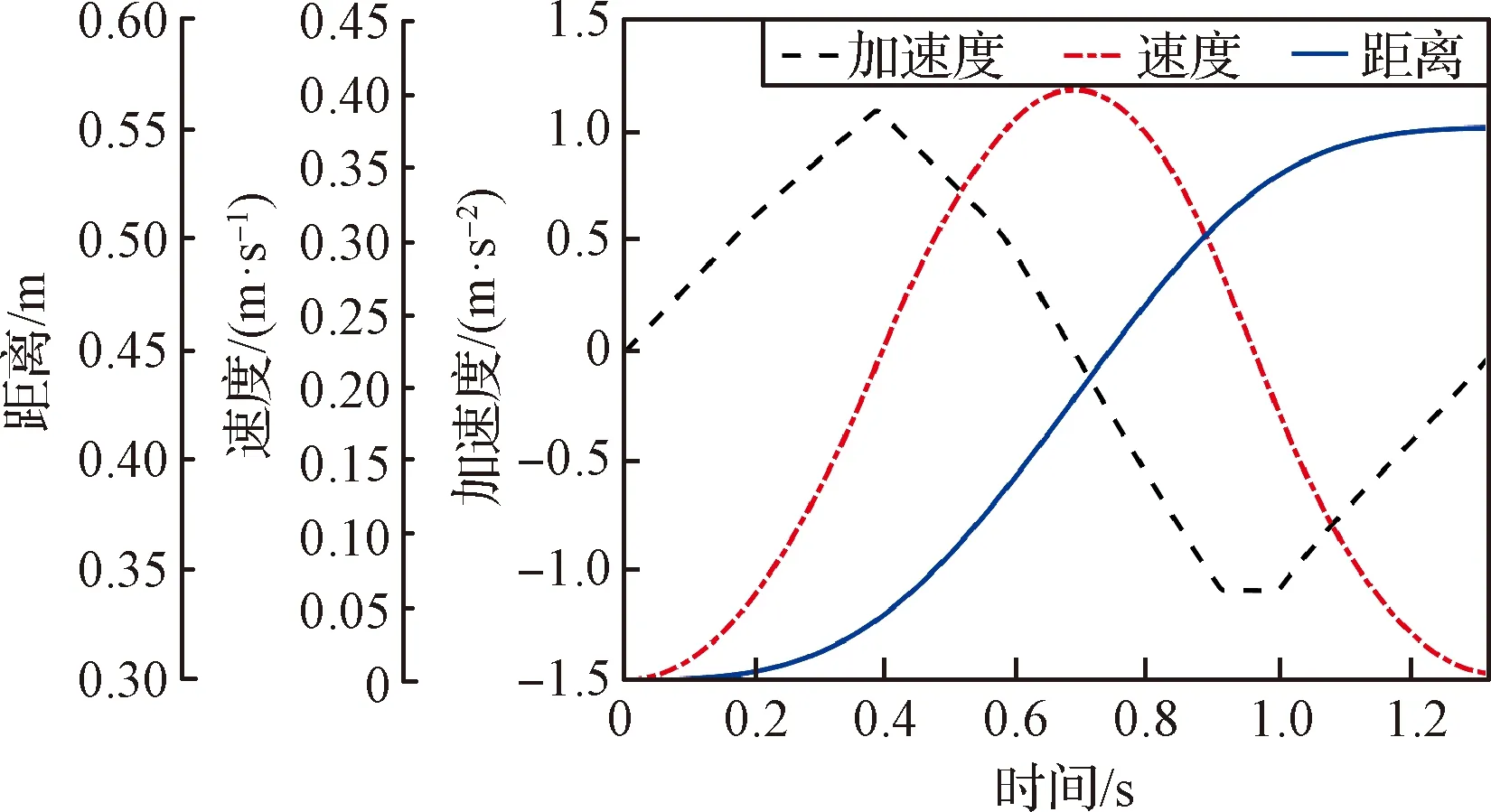
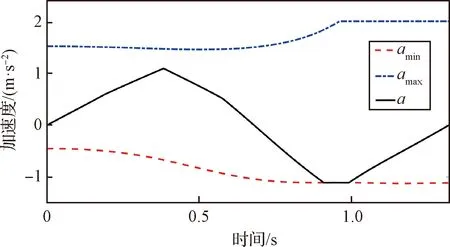
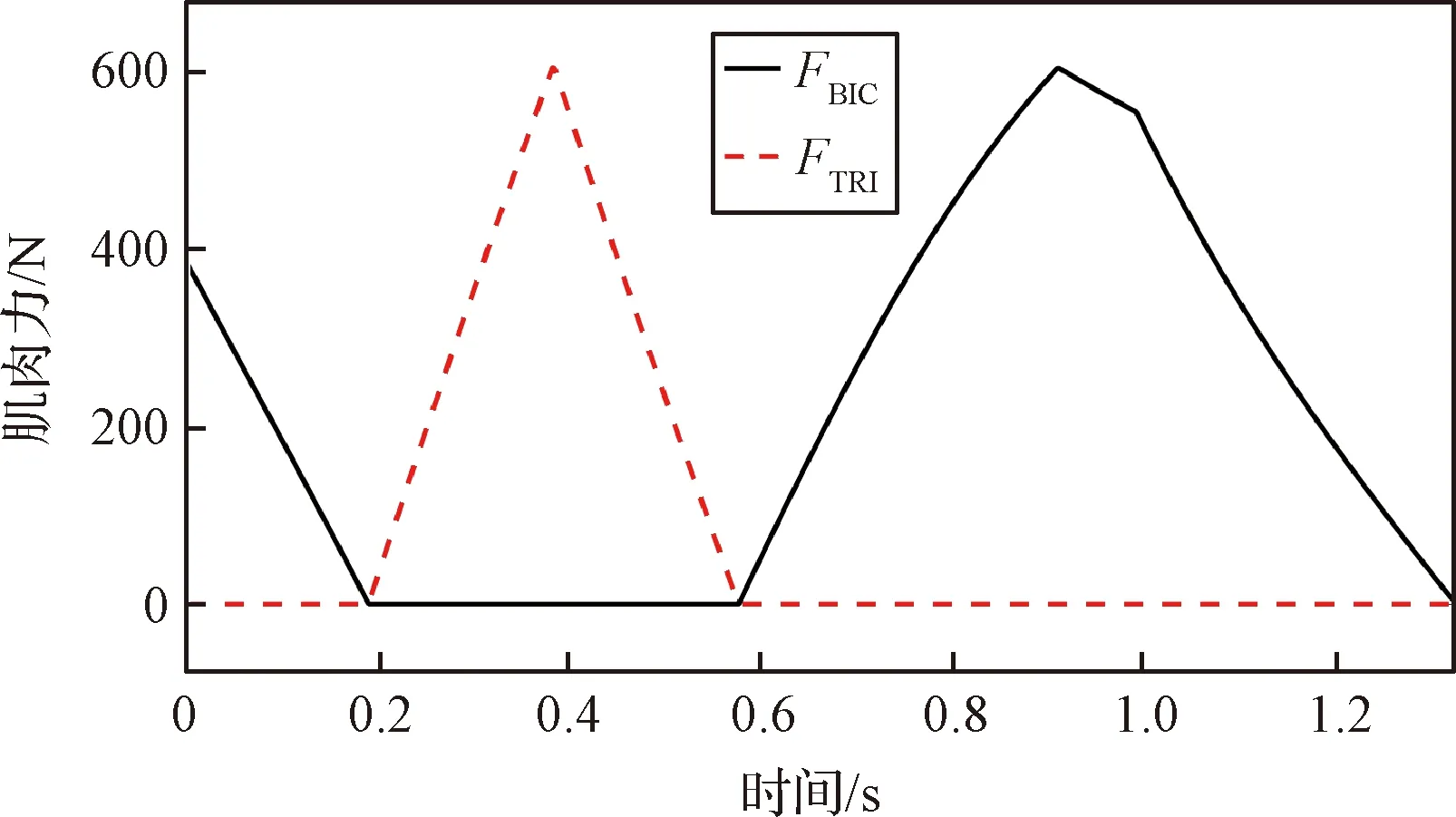
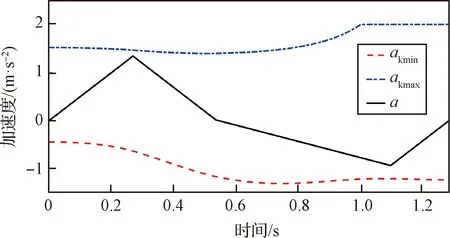
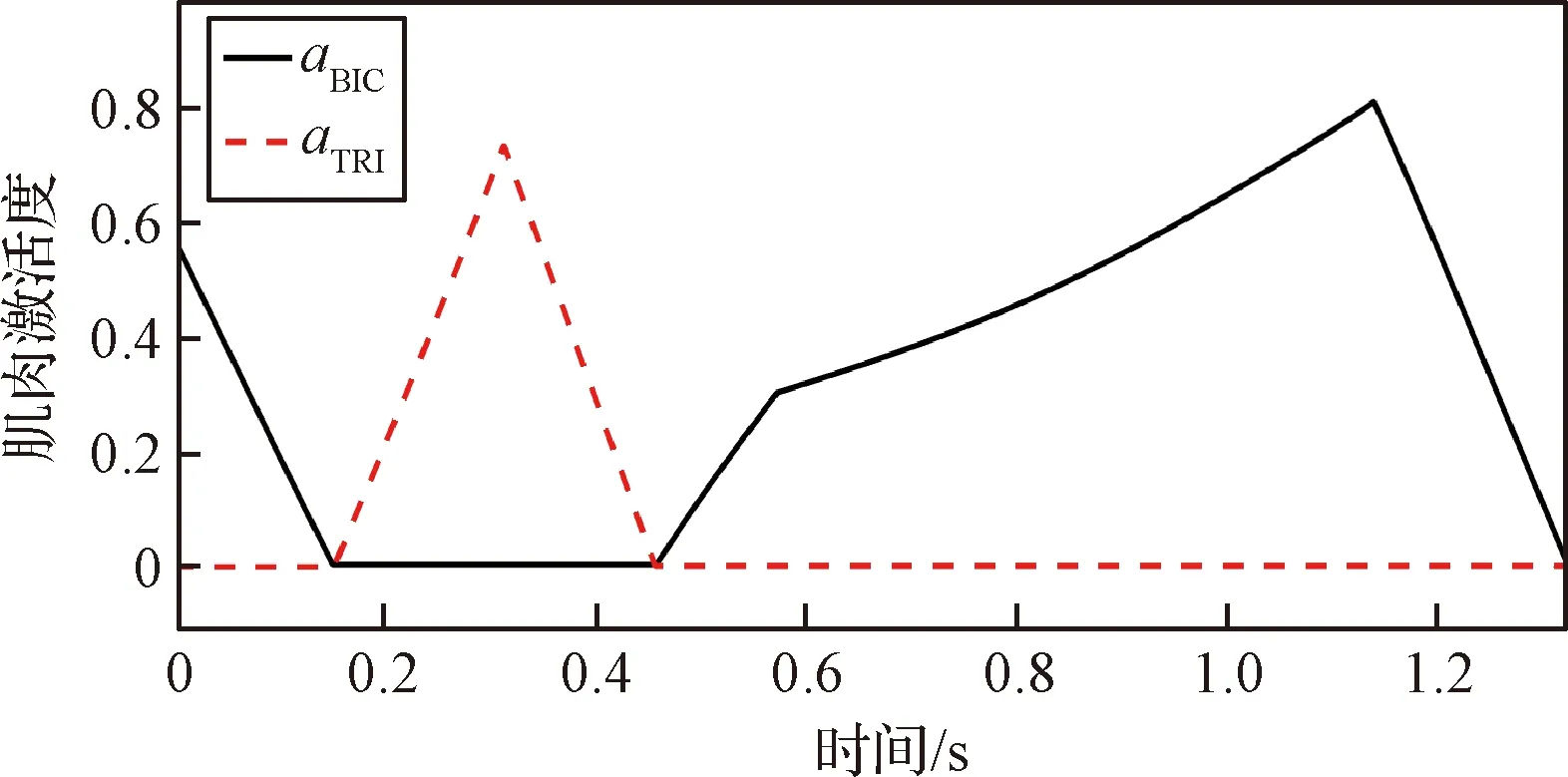
如果在θ1取最小值時,點C在冠狀面的投影也位于B點左側,那么隨著B點的運動,點C在冠狀面的投影有可能變為B點右側。如果在θ1取最大值時,點C在冠狀面的投影也位于B點以左,那么在整個運動過程中,點C在冠狀面的投影始終位于B點以左,即始終是圖2(c)中的情況。此時,l2cos(θ1+θ2)<0,lp>0。此種情況出現的條件為lp 由以上分析可知,若lp<36.2 mm時,可以保證在運動過程中,|lp|始終小于|l2cos(θ1+θ2)|,a2max小于a1max。在實際的訓練設備中,lp的值遠小于36.2 mm,因此,物體的最大加速度主要受到肘關節力矩T2和航天服手套不被撕裂的限制。 為了建模方便,將與肘關節有關的肱二頭肌(BIC)和肱三頭肌(TRI)等效為單頭肌肉,通過其等效長度確定肌肉上端的等效位置點,其等效長度的計算方法采用文獻[17]的計算方法。 根據Hill肌肉模型,肌纖維力Ff: Ff=FCE+FPEE (8) 式中:FCE為肌纖維主動力,FPEE為肌纖維被動力。 由文獻[18]可知,肌纖維主動力與肌肉激活度A、肌纖維的長度lM及肌纖維收縮速度vM相關,即肌纖維主動力FCE: FCE=F(A,lM,vM) (9) 肌肉激活度A反映的是肌肉在神經系統的刺激下受到激活的程度,激活度越高,肌肉產生的主動收縮力也越大。在一定程度上,肌肉的激活度可以從肌電信號角度來表征,通過采集該肌肉處的皮膚表面肌電信號,并做歸一化處理得到肌電信號強度,以肌電信號強度作為輸入,經過肌肉激活度模型,來表征肌肉激活度。其取值范圍為[0,1]。 肌纖維被動力只與肌纖維的長度有關,即肌纖維被動力: FPEE=F(lM) (10) 肘關節的骨骼肌模型如圖3所示。圖中,d1,d2分別為肱二頭肌兩個止點到肘關節旋轉中心的距離,d3為肱三頭肌上止點到肘關節旋轉中心的距離,θ2表示肘關節的角度。肱三頭肌是沿肘關節的外包絡曲面分布的,將該曲面簡化為半徑為R2的球面。 圖3 肘關節骨骼肌模型Fig.3 The skeletal muscle model of elbow joint 肌肉拉力線可以近似為直線,根據圖3的幾何關系可得,肱二頭肌的肌肉長度lBIC: 因此,肌纖維長度lMBIC: (11) 式中:lTBIC為肱二頭肌的肌腱長度之和,可以認為是常量;φBIC為肱二頭肌的羽狀角。 肱三頭肌的肌纖維長度lMTRI: (12) 式中:θ0為肱三頭肌處于最大等長收縮狀態時肘關節的關節角度,φTRI為肱三頭肌的羽狀角。 對于肌力臂的計算,采用虛功的方法求解動態肌力臂[19],解得肱二頭肌肌力臂dBIC: (13) 肱三頭肌的肌力臂dTRI: (14) 肘關節的總力矩T2: T2=FfBICdBIC+FfTRIdTRI-Tf (15) 式中:Tf為航天服的肘關節阻尼力矩,其值由文獻[20]確定,如下式所示。 (16) 將式(8)-式(14)代入式(15)中,即可求得肘關節的總力矩與肘關節角度之間的函數關系式 (17) 將式(17)代入式(6)、式(7)中可求得物體的最大加速度 (18) 由圖1的幾何關系可知,肩關節角度θ1與肘關節角度θ2存在一定的約束關系。可將式(18)簡化為 (19) 勻加速階段以最大加速度進行運動,根據式(19)可知,最大加速度為關節角度、角速度的函數,即在該階段的任意t時刻時物體被移動的距離 (20) 式中:t1為勻加速階段開始的時間,l0為勻加速階段開始時物體到冠狀面的距離。 形如式(20)的積分很難求出解析解,因此傳統的相平面法無法完成此類問題的速度規劃。 七段S型加減速曲線中,勻速段的存在條件是物體達到了最大速度。由圖1和圖3的幾何關系可得,由肱二頭肌決定的目標物體的最大速度 (21) 式中:vmaxBIC為肱二頭肌最大收縮速度。 由肱三頭肌決定的目標物體的最大速度 基于此,在充分研究企業管理者特質、內部控制以及企業價值關系的過程中,要建立對應的檢驗模型,為依據模型就能對相關參數的關系進行分析,并且要結合實際情況分別建立對應的管理者檢驗模型,從而合理性考量三者的關系,進一步提升模型分析的時效性。 式中:vmaxTRI為肱三頭肌最大收縮速度。 目標物體的最大速度與肘關節角度的關系如圖4所示。在肘關節角度為0°時,由肱三頭肌決定的最大速度為0,實際上,此時規劃后的速度也一定為0。因此,在搬運物體的過程中,目標物體的速度很難達到最大速度,勻速階段不存在。 圖4 物體的最大速度與肘關節角度的關系Fig.4 The relationship between the maximum velocity of the target object and the elbow joint angle 對于人體上肢來說,物體的最大允許加速度未知,但肌肉激活度的范圍為[0,1],因此,通過調整肌肉激活度來改變物體的加速度是較為合適的方法,可將動態的加速度約束轉變為靜態的肌肉激活度約束。 肌肉激活度的變化有三種情況:增加、減小和不變。前兩種情況顯而易見是存在的。當肌肉激活度不變時,物體的加速度近似不變。若物體的加速度為0時,則物體處于勻速狀態,此時肘關節力矩近似始終等于航天服阻尼力矩,肌肉激活度近似保持不變。由于肘關節的最大力矩大于航天服阻尼力矩,因此此時肌肉激活度一定不為1。由于勻速階段不存在,因此這種情況不存在;若物體的加速度為非零定值時,考慮到時間最短的原則,該加速度一定為最大加速度,即達到了最大加速度限制。對于肌肉激活度規劃來說,最大加速度限制就是肌肉激活度達到了1時的加速度,即勻加速階段肌肉激活度一定近似為1。因為肱二頭肌和肱三頭肌是一對拮抗肌,其中某根肌肉收縮時,另外一根肌肉一定放松,因此其肌肉激活度可能會始終為0。 由上述分析可知,在肌肉激活度規劃中,肌肉激活度的變化只存在四種情況:增加、減小、始終為0、始終為1。 根據式(19)可知,物體的加速度與時間的關系為 (22) (23) 式中:y0為初始時刻物體到冠狀面的距離。 圖5 A、B、C、D點的位置Fig.5 Location of points A, B, C and D 根據起始位置、目標位置和航天服在充氣后肘關節自然彎曲的角度θT0的不同情況,可將搬運過程分為表1所示的6種情況,其中的A、B、C、D點的位置如圖5所示,此時θ2=θT0=30°。 6種情況下的起始位置和終止位置的肌肉激活度見表2,“+”表示肌肉激活度不為0。 表1 不同起止點的分類情況Table 1 Classification of different starting and ending points 表2 各情況下的起止點肌肉激活度Table 2 Muscle activation at start and stop points under different cases 通過分析起始位置和終止位置,就可得到各肌肉起始時刻和終止時刻的肌肉激活度,以Case 5為例,肱二頭肌起始時刻的肌肉激活度 (24) 肱三頭肌終止時刻的肌肉激活度 (25) 式中:θ0和θd分別為起始時刻和終止時刻的肘關節角度。 在實際的運動過程中,由于運動距離的不同,Case 1、Case 3、Case 4、Case 6又可各分為兩種情況,共計十種情況。本文僅以Case 4為例,其肌肉激活度規劃如圖6所示。 圖6 Case 4情況下的肌肉激活度規劃Fig.6 Muscle activation planning in Case 4 Case 4a和Case 4b兩種情況下肱二頭肌和肱三頭肌的肌肉激活度與時間的關系如式(26)和式(27)所示。 Case 4a: (26) Case 4b: (27) 式中:J為肌肉激活度的變化率。 將式(26)和式(27)代入式(22)即可求得各個階段的加速度。以Case 4a為例,在終止時刻,肱二頭肌的肌肉激活度為aBICd,因此 aBIC0-Jt1+J(t2-t1)-J(t3-t2)=aBICd (28) 令t1=Tt1,t2-t1=Tt2,t3-t2=Tt3,代入式(28)可得 因此,給定Tt1和Tt2,即可求得在該種情況下肱二頭肌和肱三頭肌的肌肉激活度與時間的關系。 采用Matlab/Simulink搭建上肢模型如圖7所示。 圖7 上肢Simulink模型Fig.7 Upperlimb model by Simulink 根據約束條件可知,物體在最終時刻的速度為0,位移為目標物體的搬運距離Δy,即 (29) (30) 式中:Δy=yd-y0,yd為目標物體的給定位置到冠狀面的距離。 通過聯立式(29)和式(30),可以唯一確定Tt1和Tt2的值。在本文中,通過標準粒子群算法求解Tt1和Tt2的值。 將Tt1和Tt2的值輸入到圖7所示的模型中,獲得最終時刻的速度v及位置L,以此構建多目標優化算法的適應度函數f(x): f(x)=q1|v|+q2|L-yd| (31) 式中:q1和q2分別為速度誤差和位置誤差的權重。 根據適應度,更新種群的位置,反復迭代之后,即可求得最優解。 本文設計的算法程序流程圖如圖8所示。 圖8 算法流程圖Fig.8 The flow chart of the algorithm 在Matlab2018編程環境下驗證本算法。取目標物體的質量M=200 kg,y0=0.3 m,yd=0.55 m。航天服手套被撕裂的加速度aglove=2m/s2,J=3,速度誤差的權重q1=19,位置誤差的權重q2=115,人體及肌肉的各項參數設定見表3,肱二頭肌和肱三頭肌的其他結構參數按文獻[21]總結的數據設定,見表4。 可通過以上算法可解得結果如下: Tt1=0.3838 s,Tt2=0.5666 s,Tt3=0.3696 s。 運動過程中,肱二頭肌和肱三頭肌的肌肉激活度Tf如圖9所示,目標物體的加速度、速度、目標物體到冠狀面的距離如圖10所示。 表3 人體及肌肉參數Table 3 The parameters of the human body and muscle 表4 肱二頭肌和肱三頭肌的結構參數Table 4 Structual parameters of the biceps and triceps 圖9 肌肉激活度曲線Fig.9 Muscle activation profile 圖10 規劃結果Fig.10 Planning results of the algorithm 根據圖9和圖10可知,經過本文算法的規劃之后,肌肉激活度進行了勻速的增加或減小,在末端時刻,物體的速度、加速度均為0,位置達到了給定位置0.55 m。肘關節的輸出力矩連續變化,沒有發生突變。在整個運動過程中,物體的加速度連續變化,實現了較好的規劃效果。 將此過程中的加速度和加速度限制amin,amax繪在同一張圖中,如圖11所示。由圖可知,實際加速度可以較為貼合的靠近加速度限制,并沒有超出允許的加速度范圍。此過程中的肱二頭肌和肱三頭肌的肌肉力FBIC和FTRI如圖12所示。 采用文獻[11]中的方法進行求解,將其對加速度的約束條件變為本文中的加速度約束條件,限制最大加加速度Jmax=5m/s3,解得規劃時間為1.324 s,而本文算法求得的時間為1.322 s。 圖11 加速度限制曲線Fig.11 Acceration constraints 圖12 肌肉力曲線Fig.12 Muscle force profile 文獻[11]規劃結果的加速度和加速度限制如圖13所示。對比圖13和圖11可發現,本文所采用的方法能達到加速度限制的邊界并維持在加速度邊界一段時間,而文獻[11]所采用的方法只能在加速度的兩個極值點達到加速度邊界,而沒有加速度基本維持在加速度邊界的階段,因此求解出的規劃時間略長。 圖13 加速度限制曲線Fig.13 Acceration constraints 根據文獻[11]的規劃結果反解出肱二頭肌和肱三頭肌的肌肉激活度如圖14所示。從圖中可知,該方法無法對肌肉激活度進行約束,求解出的肱二頭肌肌肉激活度在0.6 s左右出現轉折點,即肌肉激活度的變化率出現變化。對于航天員來說,肌肉激活度的變化率維持不變是比較符合人體生物力學的做法。本文求解的肌肉激活度的變化率只在肌肉激活度為0或者1時發生變化,即肌肉激活度勻速增加,對于航天員來說是較為合適的搬運方法。 圖14 肌肉激活度曲線Fig.14 Muscle activation profile 本文建立了上臂和前臂的動力學模型及肘關節的骨骼肌模型,分析了航天員在身著航天服時搬運物體的十種情況,并對肌肉激活度進行規劃。將動態的加速度約束轉變為靜態的肌肉激活度約束,通過粒子群算法求解出各個階段的時間,從而實現了目標物體的在動態加速度約束下的時間最優速度規劃。在多人協同虛擬訓練和建立“虛擬人”模擬仿真系統中,提供φ0機器人和虛擬人一個相對符合人體生物力學的給定速度,具有實際應用可行性。 下一步的研究包括: 1)對較復雜的空間六自由度物體的運動過程進行分析; 2)將作業時間和作業過程中消耗的能量作為優化目標進行多目標優化; 3)根據被訓練者的感官體驗,確定肌肉激活度的變化率J的取值;采集每個被訓練者的肌電信號,對結果進行動態調整,以增加算法的適用性。1.2 肘關節及其骨骼肌模型
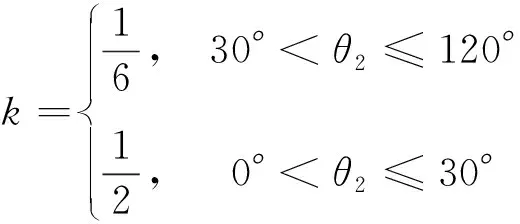
2 基于肌肉激活度的速度規劃
2.1 勻速階段存在與否的分析
2.2 肌肉激活度規劃

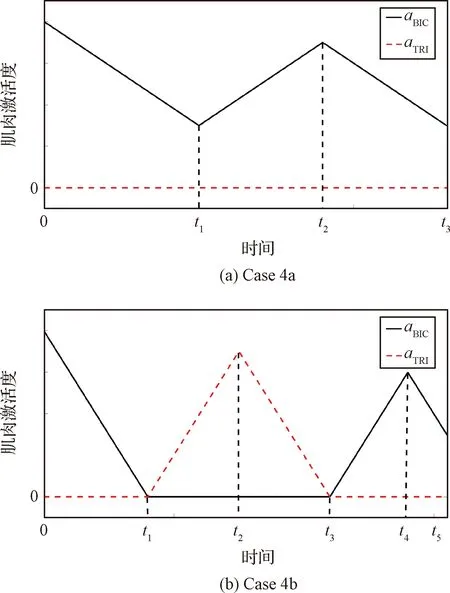
2.3 粒子群算法求解
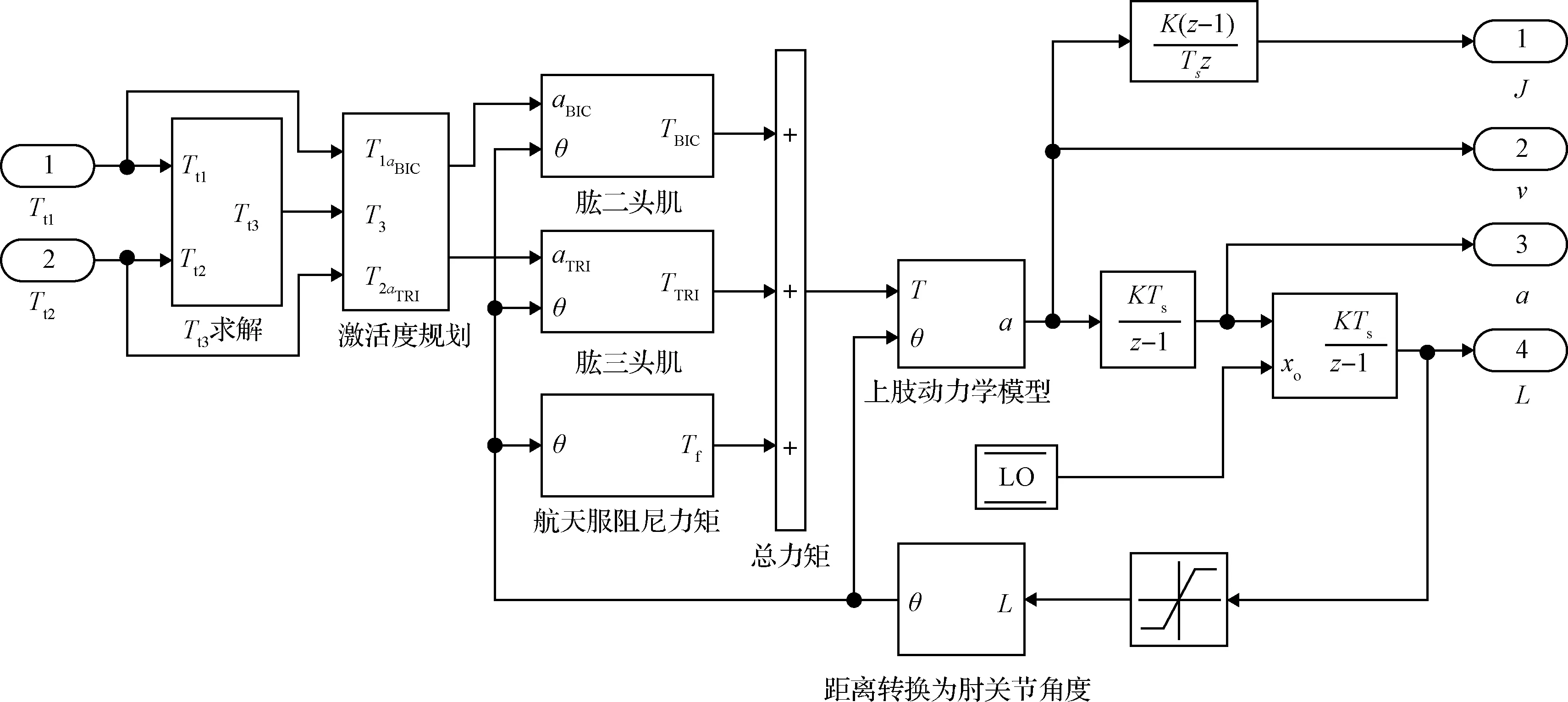
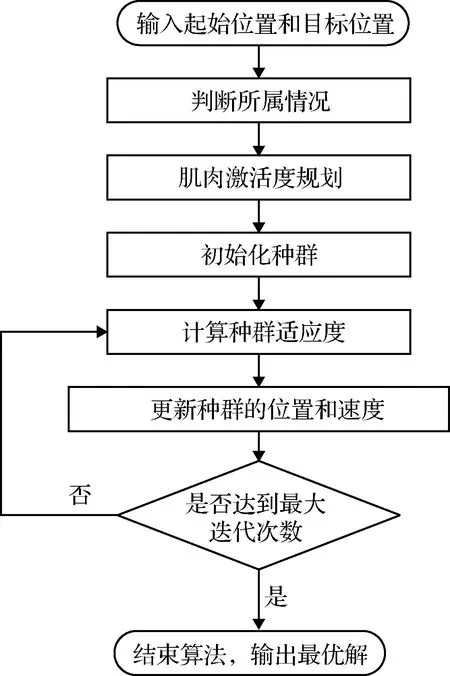
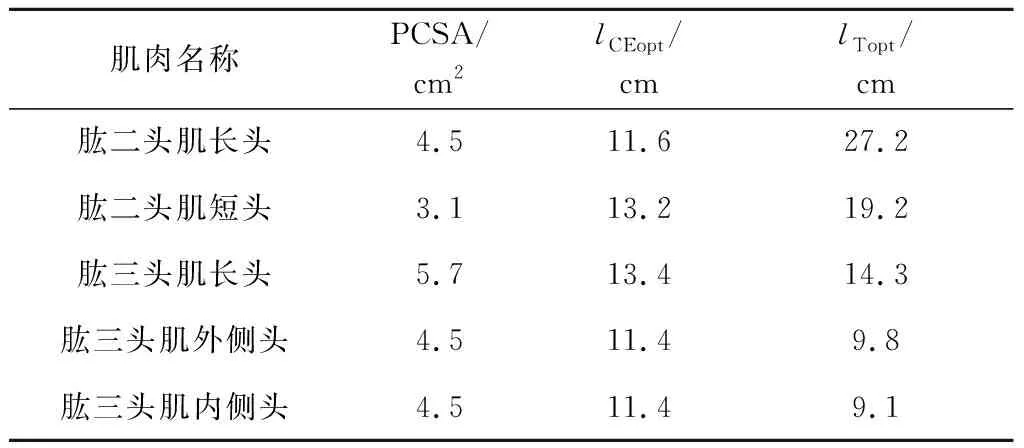
3 仿真算例

4 結 論

