鈦合金板裂紋損傷聲發射源的信號特征分析

魏鑫成， 黃麗霞， 戴雪梅， 石文澤， 李煦釗

（1.南昌航空大學無損檢測技術教育部重點實驗室，南昌330063；2.中國航發南方工業有限公司，湖南株洲412002）

0 引 言

鈦合金材料擁有強度高、密度小、耐腐蝕性能好、熱穩定性能好等優勢，在航天、航空、醫療、核電、化工等領域獲得了大量應用［1］，特別是在航空航天領域，鈦合金主要用于制作飛機發動機重要部件，如擴壓器機匣等［2］。但是，由于飛機發動機通常工作在惡劣環境中，各部件不斷經受工作溫度以及疲勞載荷的作用，容易產生疲勞裂紋，對使用壽命產生嚴重影響，因此需要對其進行動態無損檢測，及時發現其工作中出現的損傷，對于保障飛機安全性有重要的意義。

聲發射技術是一種動態的無損檢測技術，可以實時檢測到材料內部結構變化（聲發射源）產生的彈性波，并通過波形特征對損傷進行定位和判斷。裂紋擴展是一個重要的聲發射源，由它所產生的聲波可以反映裂紋的本質特征，與其他檢測方法相比，聲發射檢測能夠評估裂紋的動態特征，非常適合于檢測材料和結構的動態行為［3-5］。

近年來，已有一些實驗研究利用聲發射檢測對鈦合金聲發射源進行定位與動態評估，劉哲軍等［6］依據定位集中區內的特征參數，將環形容器的定位集中度分級，并對環形容器聲發射嚴重性進行判別。馬方慧等［7］通過對鈦合金進行拉伸力學實驗，獲得力學性能與特征參數之間的關系，并進行了特征分析與聲發射源定位研究。何攀等［8］在直升機槳轂裂紋源仿真分析中，對聲發射信號傳播特性與信號特征參數有詳細的研究。但是這些實驗對聲發射源類型和模態的分析研究較少，有一些專門研究聲發射模態的工作［9-10］，但鮮有對鈦合金材料的研究報道。本文開展鈦合金板裂紋聲發射源傳播特性研究，通過傳播模態分析，有助于進一步對鈦合金板中的裂紋聲發射源進行解釋。通過建立聲發射源，觀察其產生的彈性波在鈦合金板中的傳播，采用不同類型的聲發射源模擬裂紋擴展，利用不同的上升時間激發的信號，經小波變換獲得時頻圖，與頻散曲線對比分析聲發射模態，該結論為鈦合金損傷實驗提供依據。

1 聲發射源的表示方法與仿真條件

1.1 聲發射源的表示方法

本文采用適用于位移不連續的等效體力理論來表示聲發射源的方法［11-12］，從而產生與裂紋或者位錯運動相同的彈性波傳導。在力學理論中，大小相等、方向相反且平行的2 個力稱為雙力，如果它們位于同一條直線上，則稱為極子；如果它們位于不同的平行線上，則稱為力偶［13］。

本文主要研究兩種聲發射源類型，平行鈦合金板面與垂直鈦合金板面方向的聲發射源，因為在鈦合金板內，聲發射源沿X軸或Y軸方向傳播是相同的傳播方式，所以不必重復考慮Y軸方向聲發射源類型。因此，本文研究沿X 軸與Z 軸力源方向的雙極子源，它們表示不同類型的裂紋源，如圖1 所示。

圖1 兩種聲發射源表示方法

對雙極子源施加的力源函數通常可以取升余弦函數的形式［13］：

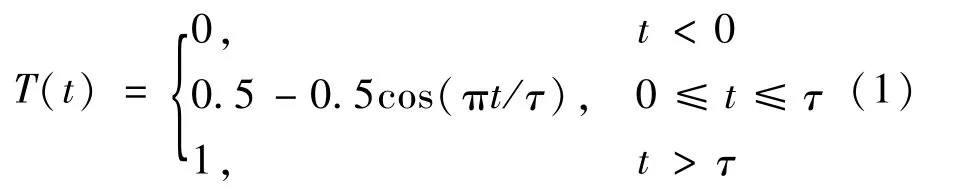
式中：τ為上升時間。不同的上升時間能夠獲得不同中心頻率的源函數，從而模擬不同頻率的聲發射源。該函數作為偶極子源函數產生的信號通常與斷鉛信號類似，本文仿真的模擬聲發射源即取自這種源函數，取上升時間為0.75、1.5、3.0 μs作為3 個頻率的聲發射源進行研究。

1.2 仿真條件

為了準確地模擬聲發射現象中彈性波隨時間的響應，建模需要選擇合適的時間分辨率，而時間分辨率即為仿真的時間步長。研究中利用時間間隔公式和單元長度公式：

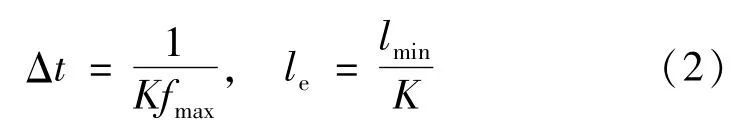
式中：Δt為時間間隔；K 為空間和時間采樣的比例縮放因子，本文K取10；fmax為聲發射信號最高頻率；le為所選取單元長度；lmin為聲發射信號最小波長，常用聲發射信號頻率在1 MHz以下，因此fmax取為1 MHz，得仿真時間間隔為0.1 μs，

橫波波速cS與縱波波速cL的計算公式如下：

λ、μ分別為材料的拉梅常數，

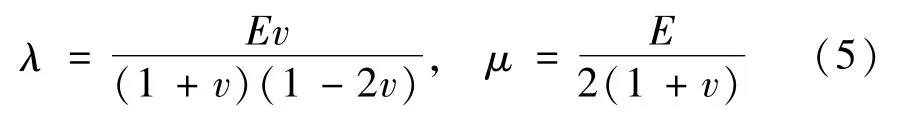
材料的拉梅常數由材料的彈性模量E與泊松比σ計算出，代入式（4）即可算出cS、cL。本文所用comsol內置鈦合金材料的參數如下：T ＝20 ℃，E ＝109.4 GPa，σ ＝0.338，ρ ＝4 500 kg／m3，cS＝3 009 m／s，cL＝6 082 m／s。代入式（2）、（3）計算可得lmin為3 mm，le單元長度為0.3 mm。

2 Lamb波模態與頻散

當板狀結構的板厚度尺寸遠小于它其他兩個方向的尺寸時，在一個激勵作用下形成的波主要是板波，即Lamb波［14-15］。超聲Lamb 波波速與頻率f、板厚b 的關系：

對稱型（S）

反對稱型（A）

式中：f為聲波頻率；b為板厚；ktl為無限大介質中縱波聲速；kts為無限大介質中橫波聲速；vp為Lamb 波的相速度。

頻散曲線指的是不同模式波的速度是波頻率與板厚的函數關系式。Lamb波在作為波導的板中傳播時，由于受結構的厚度影響，使得在結構中傳播的Lamb波的速度隨著波的頻率改變而改變，從而導致Lamb波的幾何頻散。在低頻厚積的情況下至少存在兩種模式，隨著頻厚積的增加，會產生更多的模式，即Lamb波具有多模式特征。

用傳導距離、群速度與時間的關系，將群速度曲線疊加到小波時頻圖上，從而獲得疊加鈦合金板頻散曲線的時頻圖。對于平板聲發射，由于板厚遠小于聲波的波長，聲發射源在平板中主要產生縱波擴展波（S0對稱模態）、彎曲波（A0 反對稱模態）、少量的高階波［22］。在高頻成分，擴展波（S0）比彎曲波（A0）更加豐富。兩種波位移的相對幅值同激勵源方向有關，斷裂產生的聲發射信號通常以擴展波（S0）為主，高頻含量較為豐富。而當激勵力源作用方向與板平面垂直時，產生的波形是擴展波與彎曲波的組合。擴展波波速較快，會率先到達，而后到達的是速度較慢，有頻散效應但是占有主導成分的彎曲波［16-17］，無論波的對稱模式還是非對稱模式，最低階基本模態（S0、A0）都包含了大部分能量，因此，本文結果圖只考慮疊加S0 與A0 模態。圖2 為6 mm鈦合金板的群速度頻散曲線。

圖2 6 mm鈦合金板群速度頻散曲線

3 仿真測試與結果

3.1 仿真模型

根據實驗材料，設定鈦合金板的幾何大小為300 mm×300 mm×6 mm，如圖3 所示。在鈦合金板左側中心（-150，0，3）與左側表面（-150，0，6）的一個網格單元內分別設置平行X 軸的雙極子源與平行Z 軸的雙極子源，模擬聲發射源施加力源函數。邊界條件設定固定底面，網格劃分為極細化。距聲源50、100、150 mm設置測量點A（-100，0，6）、B（-50，0，6）、O（0，0，6）（單位：mm），研究步驟的選擇為瞬態，時間間隔為0.1 μs，仿真總步長200 μs，啟動仿真計算。

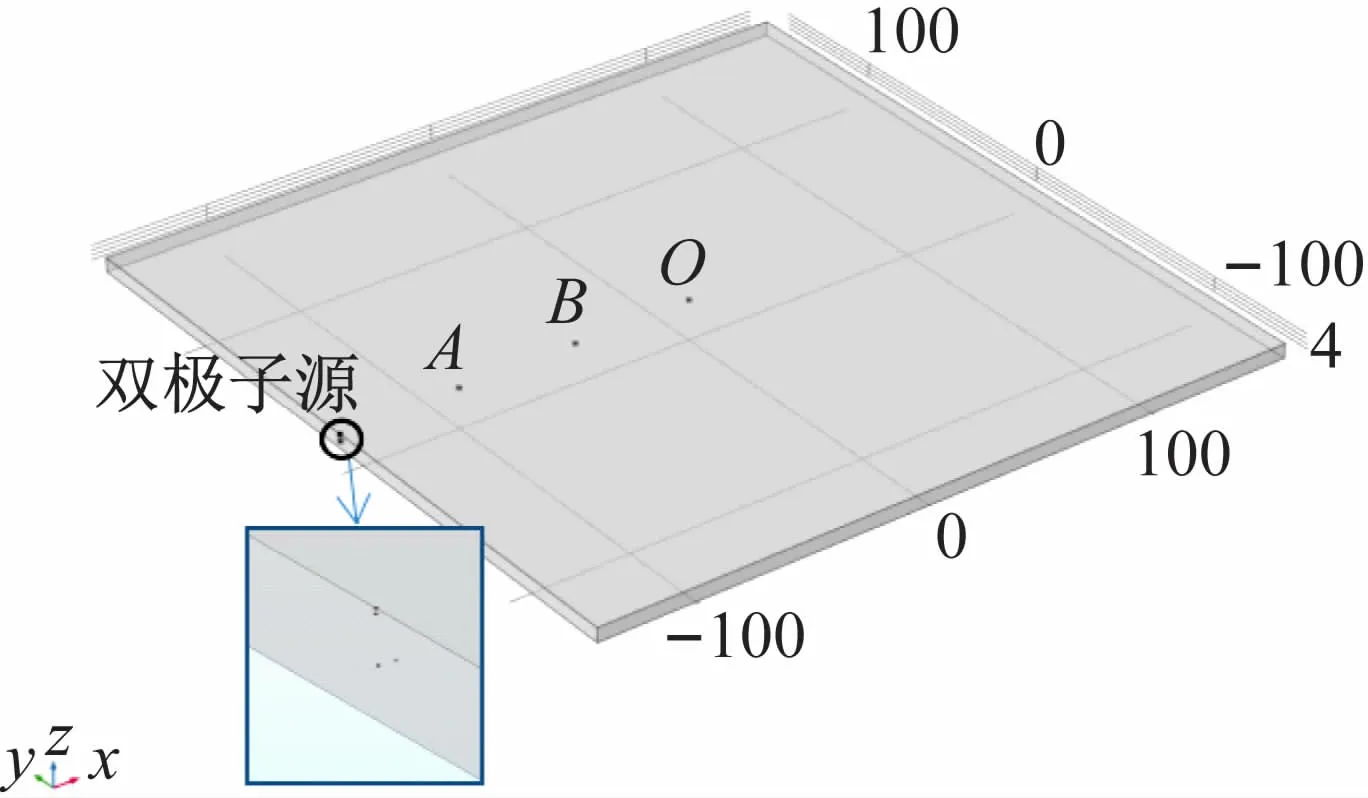
圖3 三維鈦合金板的仿真模型（mm）

3.2 仿真測試

雙極子源處于鈦合金板內部的位移波動圖如圖4所示。可以看到，仿真結果非常清晰地展示了模擬聲發射裂紋源所產生的聲波路徑，一系列的位移波動圖能很好地解釋聲發射信號的傳播過程。

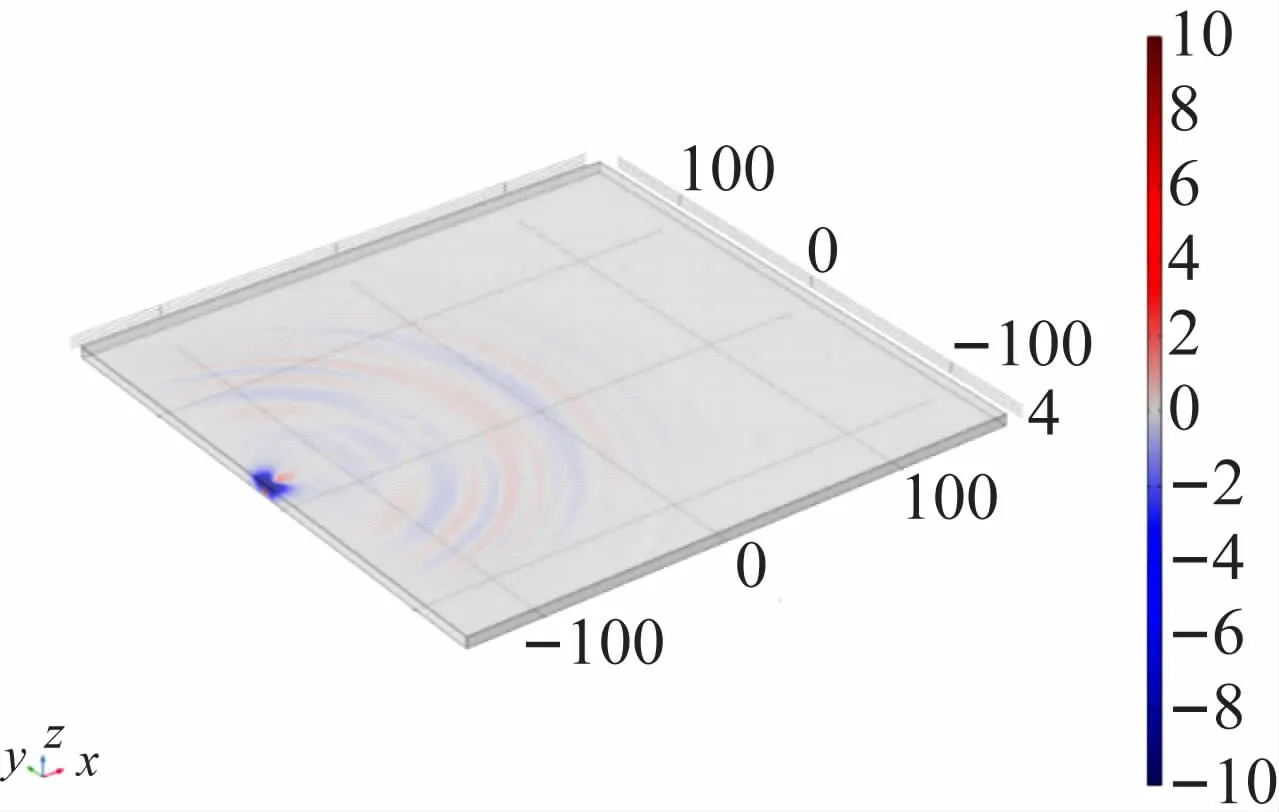
圖4 聲發射信號傳播圖（mm）

采集A、B 點的位移圖，利用時差法計算波速為5 882 m／s，與理論計算值6 082 m／s接近，考慮到聲波傳播時候存在衰減與反射干擾，此仿真模型較為合理。

3.3 仿真結果分析

為了研究不同類型的聲發射源，設置了分別沿X軸與Z軸為力源方向的聲發射源，改變上升時間能使得聲發射源中心頻率發生改變。為了觀察中心頻率對模態識別與特征頻率的影響，取上升時間為0.75、1.5、3 μs進行仿真計算。設置A、B、O 點為數據采集點，進行時頻分析并疊加頻散曲線，觀察并分析傳導距離與特征頻率的關系。

（1）不同類型的聲發射信號特征分析與模態識別。上升時間為0.75 μs，X軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖5 所示。

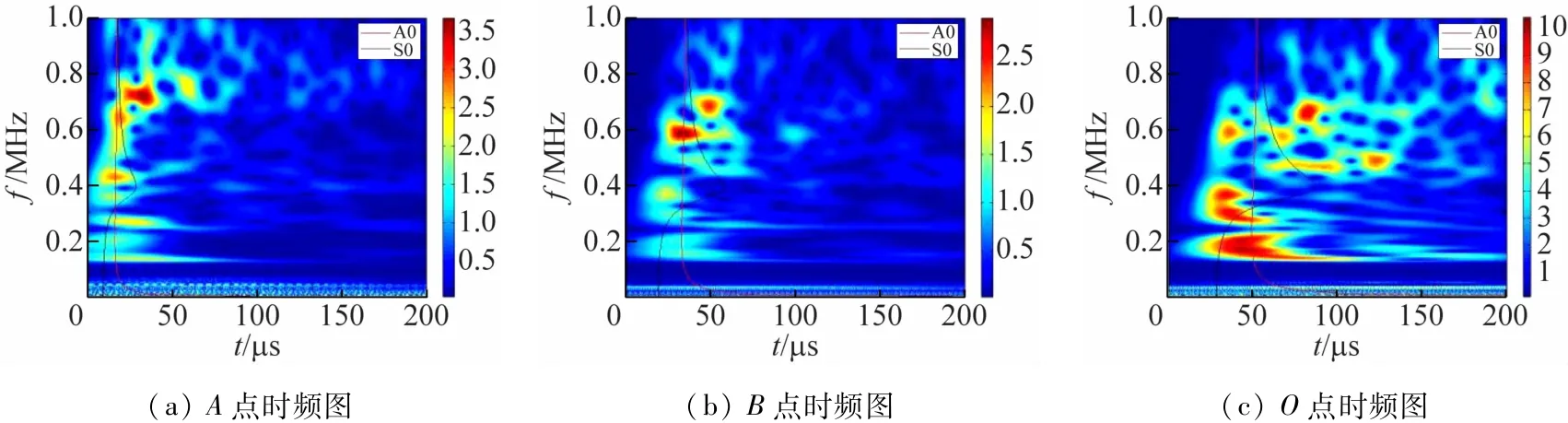
圖5 X軸源方向聲發射信號的時頻圖與頻散曲線對照

由圖5 可以看到，上升時間為0.75 μs 的聲發射信號時頻圖（a）幅值較高的紅色區域集中在600 ～750 kHz，與所設置的聲發射信號的中心頻率（667 kHz）接近，且高頻率紅色區域與S0、A0 曲線都有重合，不易識別其模態特征。因為中心頻率設置的較高，S0、A0曲線非常的緊密所導致識別問題。隨著傳導距離的增加，S0 曲線在高頻率（600 kHz）處彎曲程度逐漸增大，高幅值區域的幅值與其頻率逐漸下降，O 點采集到的數據已有多處在S0 附近的分散高頻（500 ～620 kHz）紅色區域，但其幅值低于A、B 點出現的高幅值，這是由于聲波衰減導致的。在該區域主要以S0 模態為主，且兩種模態都存在。

上升時間為0.75 μs，Z軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖6 所示。

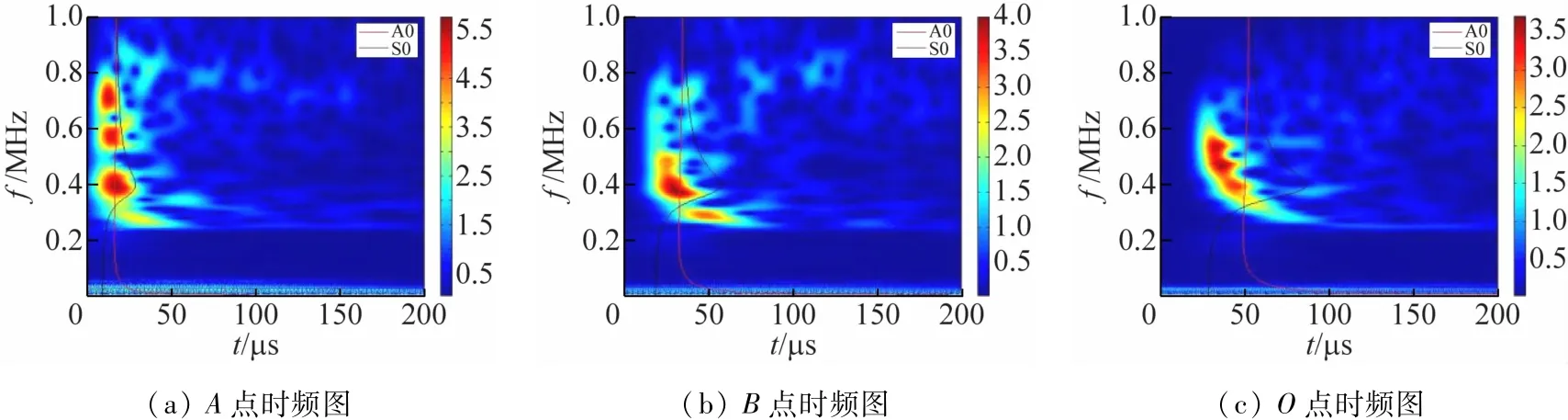
圖6 Z軸源方向聲發射信號的時頻圖與頻散曲線對照

由圖6 可以看到，上升時間為0.75 μs 的聲發射信號時頻圖（a）幅值較高的區域集中在660 ～750，530 ～590 kHz以及350 ～450 kHz，并且可以看出，3 個區域均有A0 與S0 模態，且在350 ～450 kHz 幅值區，A0 占主導地位。隨著傳導距離的增加，在S0 附近的高幅值迅速減少，在O點區域所采集的數據，只有310 kHz幅值區域有S0 模態，其他高幅值區域以A0 為主要模態。

對比圖5（c）與圖6（c）可以發現，聲發射源方向分別為X與Z的仿真結果圖截然不同，傳導距離到O點，X軸方向聲發射源產生的信號以S0 模態為主，Y軸方向聲發射源產生的信號則是以A0 模態為主，且兩種模態同時存在。這與板中Lamb波理論一致。

上升時間為1.5 μs，X 軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖7 所示。由圖7 可見，上升時間為1.5 μs 的聲發射信號時頻圖7（a）幅值較高的紅色區域集中在340 ～460 和260 ～280 kHz附近。與所設置的聲發射信號的中心頻率（333 kHz）接近，與S0 與A0 曲線都有重合，S0、A0 曲線非常的緊密，出現了與上升時間為0.75 μs 時一致的模態識別問題，不易識別其模態特征。隨著傳導距離的增加，呈現了與上升時間0.75 μs時相同的規律，S0 曲線彎曲程度逐漸增大，信號衰減高幅值區域的幅值與其頻率逐漸下降，在O 點處可以明顯看出，290 ～350 kHz 左右的紅色區域主要是S0 模態為主，但其幅值低于A、B點出現的高幅值，且兩種模態都存在。上升時間為1.5 μs，Z軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖8 所示。

由圖8 可以看到，上升時間為1.5 μs的聲發射信號時頻圖（a）幅值較高的區域集中在330 ～430 kHz，并且可以看出，該區域有A0 與S0 模態，且A0 占主導地位。隨著傳導距離的增加，在S0 附近的高幅值迅速減少，在O點區域所采集的數據，只有300 kHz幅值區域有明顯的S0 模態，其他高幅值區域以A0 為主要模態。

對比圖7（c）與圖8（c），得出的結論與上升時間為0.75 μs 時的結論一致，X 軸方向聲發射源產生的信號以S0 模態為主，Y軸方向聲發射源產生的信號則是以A0 模態為主，且兩種模態同時存在。該結果再一次印證了Lamb波的理論。

上升時間為3 μs，X 軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖9 所示。

圖7 上升時間為1.5 μs時X軸源方向聲發射信號的時頻圖與頻散曲線對照

圖8 上升時間為1.5 μs時Z軸源方向聲發射信號的時頻圖與頻散曲線對照

圖9 上升時間為3 μs時X軸源方向聲發射信號的時頻圖與頻散曲線對照

由圖9 可以看到，上升時間為3 μs的聲發射信號時頻圖（a）幅值較高的紅色區域集中在140 ～160 kHz，與所設置的聲發射信號的中心頻率（167 kHz）接近，與S0 與A0 曲線均有重合。隨著傳導距離的增加，S0 曲線彎曲程度逐漸增大，高幅值區域的幅值與其頻率逐漸下降，此時O點采集的數據紅色區域依然包含兩種模態，但已無法識別模態特征。

上升時間為3 μs，Z 軸方向聲發射源產生信號的小波時頻圖與頻散曲線結果如圖10 所示。由圖10 可看到，上升時間為3 μs的聲發射信號時頻圖（a）幅值較高的區域集中在250 ～310 kHz，且可看出該區域內包含A0 與S0 模態，由于該區域，重疊部分均是幅值最高區域，已無法對其進行模態識別。

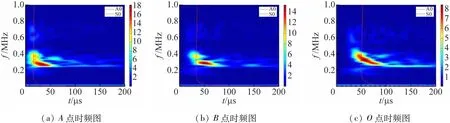
圖10 上升時間為3 μs時Z軸源方向聲發射信號的時頻圖與頻散曲線對照

兩種類型聲發射源取3 種上升時間獲得的仿真計算數據，如表1 所示。

（2）不同上升時間的聲發射源仿真結果對比分析。隨著上升時間的增加，聲發射信號的模態特征逐漸減弱，直至上升時間為3 μs 時，已無法通過模態特征判斷其聲發射源類型。

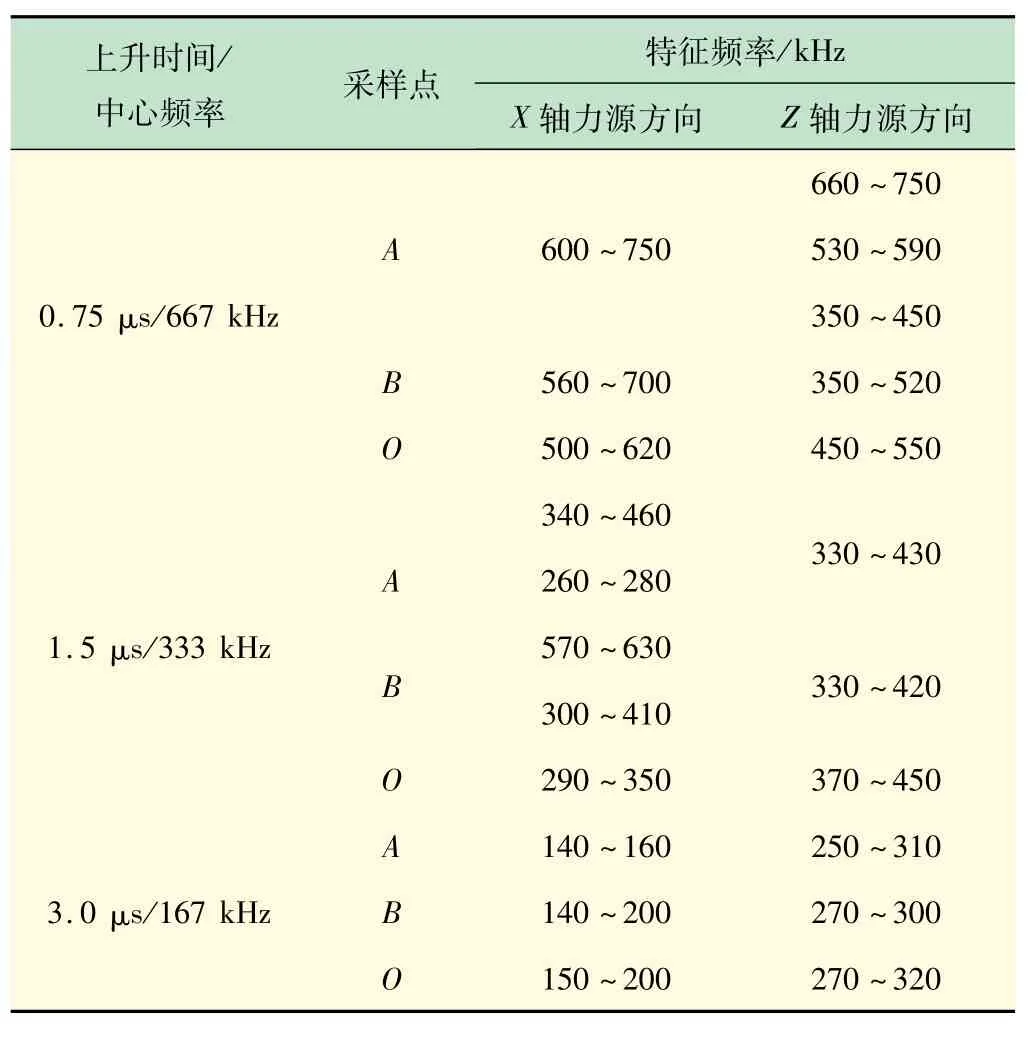
表1 3 種上升時間下聲發射源仿真計算數據

對比圖5、圖7 與圖9，即X 軸方向聲發射源不同上升時間的時頻圖，能發現由3 種上升時間獲得的A點所接收到數據的時頻圖均能大致呈現所設定聲發射源的中心頻率，如圖11 所示，兩條折線重合度較高。

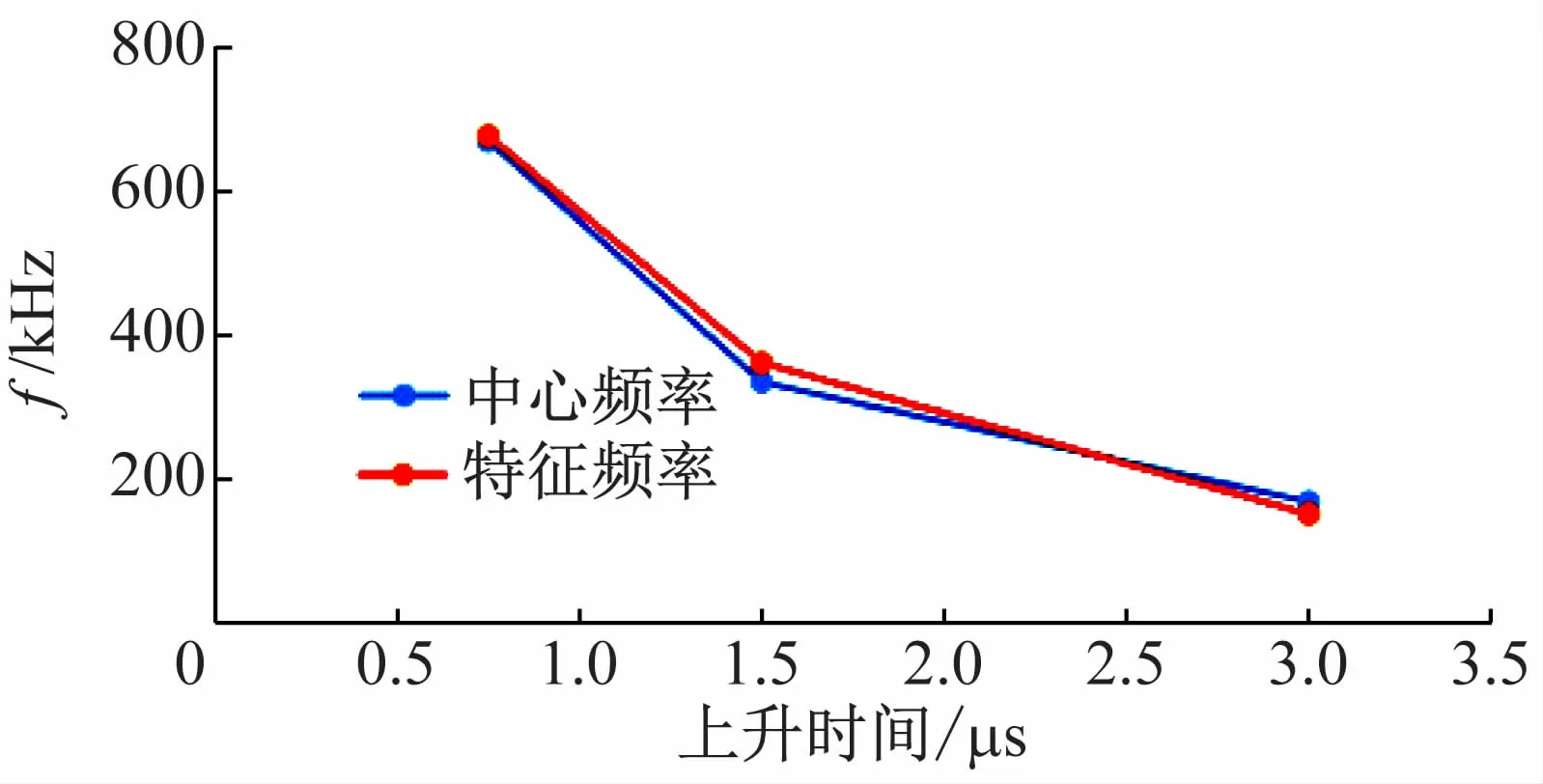
圖11 3種上升時間下在A點的特征頻率與中心頻率

隨著傳導距離的增加，雖然有衰減等不利因素干擾，但是3 種上升時間在O點表征的特征頻率，即圖5（c）、圖7（c）以及圖9（c）的高幅值區域，依然體現3種上升時間聲發射源的中心頻率變化趨勢，如圖12所示。

圖12 3種上升時間下在A點的特征頻率與中心頻率

由圖12 可以看到，上升時間短的聲發射信號的特征頻率與該時間對應的中心頻率有較大的差異，隨著上升時間的增加，差異逐漸減小。對比圖6、圖8 與圖10，即Z軸方向聲發射源不同上升時間的時頻圖，3 種上升時間獲得的A 點所接收到數據的時頻圖未能反映出其中心頻率。

但是在3 種上升時間獲得的O 點所接收到數據的時頻圖中，可以發現，圖6（c），圖8（c）與圖10（c）的高幅值區域，隨著上升時間的增加特征頻率遞減，并伴隨幅值降低，如圖13、圖14 所示。

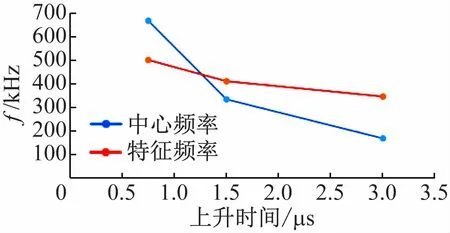
圖13 3種上升時間下在O點的特征頻率與中心頻率

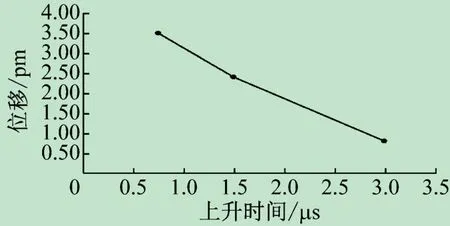
圖14 3種上升時間下在O點采集的幅值數據

4 結 論

本文利用有限元分析、小波變換與頻散曲線，對于鈦合金板裂紋損傷聲發射源進行仿真研究，分析不同類型的聲發射源，即不同方向的裂紋源，所產生波形的模態與特征頻率，并進一步研究不同上升時間對信號所產生的影響，同時對聲波傳播路徑上的多點進行數據采集，對比分析找出傳導規律。結果發現：

（1）小波變換與頻散曲線的結合能很好的提取鈦合金板裂紋損傷聲發射源的模態特征。

（2）不同類型的聲發射源的時頻圖結果是不同的，X軸方向與Z軸方向的模態特征完全不同。根據采集到的數據進行時頻分析，并觀察其模態特征能判斷聲發射源的類型。

（3）對于沿X軸方向的聲發射源，其模態特征很難在傳導距離短的采集點識別，但是傳導距離過長必會導致特征頻率和幅值的降低，因此取傳導距離在一個合適的范圍內是有必要的。本次仿真實驗，在B 點與O點的時頻圖能清楚的進行模態識別，是一個較好的傳導距離的控制。

（4）隨著上升時間的增加，聲發射模態特征的識別難度變大，最后在上升時間為3μs時刻，特征頻率與兩種模態交叉重疊，使得無法辨別其特征。