基于重構控制分配的分布式電動車容錯控制方法

歐 健，丁凌志，夏祖鈳，楊鄂川

（重慶理工大學 a．車輛工程學院；b．機械工程學院，重慶 400054）

伴隨著輪轂電機技術的發展進步，分布式驅動電動車以自身獨特的結構形式及操控性能，已成為電動汽車的一個重要發展方向［1］。相較于傳統車輛，集成主動轉向的分布式驅動電動車具有較多的控制自由度，屬于過驅動控制系統，系統中存在冗余執行器，當一個或多個執行器發生故障時，可以進行容錯控制，重構剩余正常的執行器，保障車輛在故障后也具有一定的魯棒性，提高車輛行駛的安全性與穩定性［2］。針對容錯控制問題，Hayama等［3］提出雙電機備份的控制思想，在高速行駛時對轉向失效啟用備份電機進行補償，但這種控制對某種失效模式沒有特定的控制邏輯。部分學者提出自適應滑膜控制思想使車輛對故障具有不敏感和抗干擾性［4］，對系統進行被動容錯控制可以在故障時保持一定的驅動力，但損失了車輛的部分性能。為進一步消除特定故障，文獻［5］提出二次型規劃算法設計分配控制策略，針對不同故障類型對剩余驅動力進行再分配。由于部分驅動電機故障情況下車輛仍然可以行駛，但穩定性與安全性無法得到保障，當執行機構發生故障時，故障輪無法提供預期的扭矩和轉向角，并導致無法預測的后果。因此，對這類電動車進行容錯控制是非常重要的。

基于分布式驅動電動車過驅動系統存在的冗余現象，本文提出了一種容錯控制算法，上層基于模型預測控制的運動跟蹤層，下層針對不同故障信息，提出一種基于線性二次規劃的最優控制分配，通過對正常輪胎的制動／驅動轉矩優化分配，從而跟蹤車輛的期望響應。

1 車輛動力學模型

本文主要針對車輛橫擺穩定性進行研究，采用模塊化建模思想建立整車7自由度車輛模型［6］，如圖1所示。其中7自由度主要包含橫向、縱向、橫擺運動以及4個車輪的旋轉運動，由牛頓第二定律得車輛的動力學方程為：

式（1）中：vx、vy分別為車速的縱向與側向分量；輪、左后輪、右后輪的縱向力，Fy＝［FyflFyfrFyrlFyrr］T分別為4個車輪的側向力，本文中各車輪的縱、橫向力可由Pacejka魔術輪胎公式［7］計算得出；γ為橫擺角速度；Bx、By是車輛模型的固有參數［8］。

圖1 7自由度車輛模型示意圖

車輪在滾動過程中的動力學方程表達為：

式（2）中： ωi為各輪旋轉的角加速度；Tdi為各車輪分別受到的由輪轂電機產生的驅動轉矩；R為車輪滾動半徑；Tbi為各個車輪制動器產生的摩擦力矩；Jωi表示各車輪的轉動慣量。

2 控制器結構設計

為提高電動執行機構故障后車輛的操縱穩定性，提出了一種容錯控制方法，如圖2所示。該控制方法包括3個部分：故障診斷模塊、運動控制模塊和重構控制分配模塊［9］。運動控制器以線性2自由度車輛模型為參考模型，以參考橫擺角速度和質心側偏角作輸入，采用模型預測控制的方法，使前文所搭建的車輛模型能有效跟蹤期望的運動狀態，計算出所需的總的附加力與附加力矩，由下層的重構控制分配器將總的需求力與力矩按一定規則分配給每個車輪。無故障時，以輪胎穩定性裕度最大化為控制目標，采用名義控制分配率。故障發生時，根據相應的故障類型，以輪胎穩定性裕度并結合實際故障狀況重構控制分配率。本文著重于研究驅動電機容錯重構控制分配方法，假設所期望的車輛狀態可以被測量或估計、故障信息已知。

圖2 容錯控制結構框圖

2．1 運動控制器設計

2．1．1 預測模型

模型預測控制是基于模型初始條件對系統未來狀態進行預測，并通過實時反饋來進行滾動優化，不需要精確的模型。因此選用線性2自由度車輛模型作為預測模型，以附加前輪轉角和附加橫擺力矩作為控制輸入，狀態空間方程為：

式中：

其中：a、b分別表示質心與前后軸之間的距離；δd、δa分別表示前輪轉角與附加前輪轉角；k1、k2為前后軸側偏剛度；ΔM為附加橫擺力矩。

2．1．2 預測方程

以系統當前的狀態作為輸入，通過預測方程預測出系統未來的狀態。對式（3）進行離散化，將離散后狀態空間方程改寫成增量形式，有：

根據式（4），設定預測時域為p，控制時域為m，m≤p，假設在控制時域之外，控制量不變，即Δu（k＋i）＝0，i≥m。

當前k時刻下x（k）和y（k）為已知條件，由式（4）可以對k＋1到k＋p時域內的狀態進行預測，從而進一步解得系統未來p步的預測輸出向量序列，表示為：

2．1．3 優化求解

本文的控制目標是得到期望的運動狀態，即保證車輛輸出最大化接近于參考值，同時保持控制動作平緩輸入，運動控制器的目標是使系統輸出跟蹤期望輸出，采用二次型表示的目標函數為：

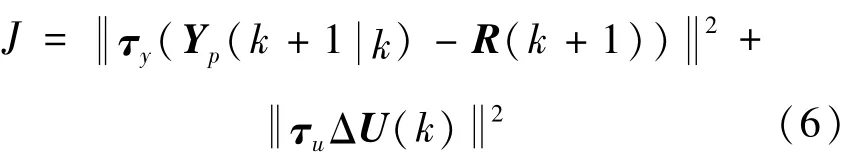
式（6）中，τy、τu為加權系數矩陣。考慮到執行器約束條件，對輸入量和輸入增量進行約束，即：

進行采樣周期優化求解，最終得到最優控制輸入增量為：

將控制系統輸入的第1個量作為實際控制輸入增量施加在所建立的車輛模型上，則有：

反復以上優化求解過程，直至求解結束。

2．2 重構控制分配器

重構控制分配器就是將運動跟蹤層所求得的附加橫擺力矩和總的縱向力需求，采用合適的分配算法把期望轉矩分配給各個執行電機，實現車輛的橫擺穩定性控制［10］。根據控制分配律決策出每個輪的輪胎縱向力Fx，在監測系統識別無故障的情況下，重構控制分配器采用名義控制分配方法；在車輛運行過程中發生某種故障時，重構控制分配器采用與該故障模式對應的重構控制分配律。

2．2．1 名義控制分配算法

無故障時，采用名義控制分配算法，以各輪輪胎利用率平方和最小為優化控制目標，旨在最大化輪胎穩定性裕量，從而保證車輛的穩定性［11］。其中，由于在工程上暫時不能對車輪的側向力進行直接控制，簡化為各個車輪縱向利用率平方和最小，目標函數為：

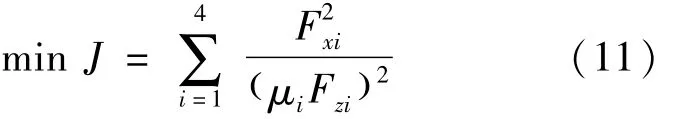
需要滿足動力學約束有：

地面附著條件的約束為：

考慮電機的轉矩輸出約束，則有：

式（14）、（15）中：μi為路面摩擦系數；Tmax為電機當前轉速n下最大輸出轉矩。

根據優化目標和約束條件，將求解轉化為加權最小二乘問題，為方便計算上述帶約束問題的目標函數，采用有效集的標準形式來求解，有：

通過求解獲得各車輪上的輪胎縱向力Fx，作為名義的控制輸入。

2．2．2 重構控制分配算法

本文研究的重構控制分配算法是基于故障觀測器所觀測到的故障信息，側重于診斷某一驅動系統的驅動力是否能正常輸出。針對一個或多個驅動執行器故障后，通過協調控制其他正常驅動系統進行輪胎力的重構分配，保障車輛的期望軌跡，提高車輛故障后的橫擺穩定性［12］。重構控制器一方面對故障執行器進行限制，防止故障進一步擴散，另一方面又針對不同的故障模式，采用相應的重構控制分配律對剩余正常的驅動系統進行轉矩分配，使執行器總的輸出力與力矩依然滿足上層運動控制器計算得到的虛擬控制量要求。

本文中提到的重構控制分配流程如下：

1）執行器無故障時，以名義控制分配率作為執行器控制輸入；

2）根據故障信息，判斷出失效模式；

3）當執行器故障時，根據相應的失效模式，采用相應的重構控制分配律作為執行器輸入［13］。分配流程如圖3所示。

根據電機的不同失效模式，重構控制分配方法如表1所示。分別討論了在單個電機失效，異側同軸雙電機失效，異側不同軸兩電機失效、同側兩電機失效及2個以上電機失效等5種失效模式。在單輪電機故障情況下，考慮驅動電機故障約束，以提高輪胎的附著裕度為目標；在異側同軸與異側不同軸電機失效情況下，僅剩余2個可控自由度的輪胎力，無法滿足車輛縱向力需求，此時著重保持故障后車輛的側向和橫擺穩定性特性；在同側兩電機及2個以上電機失效情況下，考慮到故障后車輛的安全性，進行緊急制動控制。

圖3 重構控制分配流程框圖

表1 重構控制分配方法

3 仿真實驗

在Matlab／Simulink中搭建集成容錯控制器和7自由度整車模型，輪轂電機模型采用能夠體現其特性的簡化模型，其外特性曲線高速恒扭矩，低速恒功率［14］。Matlab／Simulink整體仿真結構如圖4所示，針對執行器不同的失效模式，為驗證本文提出容錯控制算法的有效性，分別討論在單輪和雙輪失效情況下汽車的橫擺穩定性。車輛仿真參數如表2所示。

圖4 Matlab／Simulink整體仿真結構框圖

表2 整車參數

3．1 角階躍轉向工況（單輪失效）

為驗證車輛在角階躍轉向時容錯控制算法的有效性，設計工況為：初始車速為80 km／h，路面附著系數為0．8，在2 s時前輪轉角階躍輸入1°，t＝2 s時，左前輪電機完全失效，仿真結果如圖5所示。

由圖5（a）可以看出：在2 s時左前輪電機失效，無控制車輛橫擺角速度持續增加，最大值達到了0．46 rad／s，已經超出了車輛橫擺穩定性的范圍，車輛出現失穩狀態。容錯控制下橫擺角速度曲線有稍許的波動，但很快恢復穩定且不斷靠近期望值曲線，橫擺角速度最大值為0．14 rad／s，在穩定可控范圍以內。由圖5（b）可以看出：當左前輪失效時車輛的質心側偏角將偏離正常值，無法保障車輛的橫擺穩定性。紅色與藍色曲線分別為容錯控制下質心側偏角與參考模型的期望值，兩者在2 s時有稍許的波動，隨后都趨于穩定值，且容錯控制曲線更快地趨于穩定。容錯控制下質心側偏角最大絕對值為0．012 rad，期望值為0．020 rad。可見容錯控制下質心側偏角比期望值更低，對車輛的橫擺穩定性控制效果更好。由圖5（c）可以看出：在t＝2 s時，縱向車速發生抖動，但容錯控制使車輛很快就恢復到目標車速，表明容錯控制在保證車輛橫擺穩定性的同時，還能兼顧車輛的縱向速度，不改變駕駛員意圖保持車輛安全穩定行駛。圖5（d）表示容錯控制下電機轉矩分配曲線，0～2 s內按照名義控制分配，車輛正常穩定行駛，在2 s時，左前輪電機失效，根據檢測到的故障信息，車輛開始采用重構控制分配率。左前輪電機轉矩馬上置零，左后輪電機轉矩立刻增大以彌補附加橫擺力矩需求。同時，右前輪電機與右后輪電機轉矩也有少量的增加，因為當一個電機失效時，總的轉矩輸出減少，提供總的縱向力也減少，容錯控制進行協同其他電機的轉矩，在彌補橫擺力矩需求的同時，保證車輛總的縱向力，所以每個車輪單機轉矩都有增加。

圖5 角階躍工況仿真結果

3．2 正弦轉向工況（雙輪失效）

當雙輪電機發生失效時，只有剩余兩驅動電機工作，車輛的穩定性受到了巨大的威脅。為驗證容錯控制算法的有效性，設計了雙輪失效的雙移線工況進行仿真對比實驗。具體工況為：車輛車速為80 km／h，路面附著系數為0．8，方向盤轉角如圖6所示。在時間t＝2 s時左前輪與右后輪電機同時失效，仿真實驗結果如圖7所示。

圖6 前輪轉角輸入

圖7 正弦轉向仿真結果

從圖7（a）、圖7（b）可以看出：在正弦轉向工況下，無控制車輛的橫擺角速度和質心側偏角峰值分別為0．3 rad／s和0．03 rad，車輛極易失穩，從而失去控制。容錯控制下，二者相比無控制狀態更接近于期望值，且維持在車輛穩定性范圍內。表明了在雙輪胎電機失效的情況下，容錯控制車輛能有效地跟蹤期望橫擺響應。從圖7（c）可以看出：無控制下的車輛橫向位移不斷增大，在10 s仿真步長內，橫向位移達到8．6 m，此時車輛已經完全偏離了預想軌跡。容錯控制下車輛在轉向開始后，橫向位移開始增大，達到最大值2 m后，隨著正弦轉向的結束，車輛橫向偏移逐漸減小，保證車輛按預定軌跡行駛，提高了車輛的通過性。圖7（d）為容錯控制下電機的轉矩分配圖，在t＝2 s時，左前輪與右后輪電機轉矩同時變為零，右前輪電機轉矩不斷增大，左前輪電機轉矩反向增大。在容錯控制中，當雙輪電機發生失效時，電機轉矩進行了重新分配，基于重構控制分配方法，立即限制失效電機的轉矩輸出，同時分配剩余兩電機轉矩彌補車輛不足轉向，同時還要保證總的縱向力需求。因此，剩余兩電機轉矩同時反向增大來維持車輛的穩定性。其中，右前輪與左后輪電機轉矩都在最大值處受到限制，是因為考慮到電機的安全性，以電機的額定轉矩范圍內進行輸出。

4 結論

1）針對分布式驅動電動車橫擺穩定性容錯控制問題，本文總結了驅動電機的各種失效模式，并提出了相應的控制目標及約束條件，通過仿真驗證了在單輪以及雙輪驅動失效后，容錯控制策略能更好地保持車輛期望的橫擺角速度、質心側偏角以及減少車輛的跑偏量。

2）重構控制分配層，采用線性二次型方法進行輪胎力的優化分配，在執行器故障后重構控制分配率，通過設計故障時的離線仿真表明，在車輛發生故障時，容錯控制能有效地維持車輛的期望軌跡，防止故障進一步擴大且維持較好的穩定性與操縱性。

3）本文根據故障信息，總結了驅動電機的失效模式，但沒有考慮到轉向電機的失效或者傳感器的失效情況，以及幾種故障耦合下的容錯控制需進一步探索。