整體葉盤側銑加工顫振可靠性預測

張楠, 史耀耀, 陳振, 陳紅霞, 劉佳, 趙盼

(1.西北工業大學 航空發動機高性能制造工業和信息化部重點實驗室, 陜西 西安 710072;2.內蒙古工業大學 機械工程學院, 內蒙古 呼和浩特 010062;3.內蒙古工業大學 航空學院, 內蒙古 呼和浩特 010062)

整體葉盤是新一代航空發動機實現結構創新與性能跨越的核心零部件[1-2]。整體葉盤將葉片與輪盤集成一體,省去了中間榫接結構,具有減輕質量、簡化結構、減小氣流損失、提高推重比、改善安全性和可靠性等優點。整體葉盤的葉片型面復雜彎扭大,葉盤通道窄而深,且毛坯材料通常為鈦合金、高溫合金等難加工材料。使其加工難度極大,被譽為制造業皇冠上的明珠[3-4]。

多軸數控銑削廣泛應用于整體葉盤加工,側銑常用于整體葉盤型面精加工[5]。由于整體葉盤通道較深,刀具的懸長較大,徑向剛度較小,加工過程中容易發生顫振。顫振導致工件表面質量下降、刀具磨損加劇、生產效率受限[6-10]。因此,抑制顫振對加工過程至關重要。使用穩定性葉瓣圖是避免顫振最有效的方法。穩定性葉瓣圖為提高加工效率和參數優化提供了理論依據[11-17]。

傳統的穩定性葉瓣圖不考慮隨機變量對切削穩定性的影響[18-21],Duncan等[22]首次研究了隨機變量對穩定性葉瓣圖的影響;根據標準偏差,利用結構參數的平均值、上界和下界確定3條穩定性葉瓣圖的曲線;但沒有給出表示不確定度影響的量化指標。為了解決此問題,Liu等[23]研究了隨機變量對車削系統顫振穩定性預測的影響,并首次提出了可靠性葉瓣圖。可靠性葉瓣圖可用于確定顫振和無顫振區域,代替了傳統的穩定性葉瓣圖。顫振可靠性定義為加工系統的穩定性概率,可用可靠性葉瓣圖來確定。

本文應用可靠性葉瓣圖來判斷側銑加工系統的穩定性概率。將結構參數和主軸轉速視為隨機變量,以單自由度和二自由度銑削的軸向極限切削深度構造臨界穩定狀態下的性能函數;采用一次二階矩法求解銑削加工系統的可靠性模型,確定系統的穩定性概率。

1 側銑顫振的動態模型

1.1 側銑加工動態模型

側銑加工系統有2個自由度,如圖1所示。假設側銑刀有Nt個刀齒,則動態切屑厚度可以表示為[24]

hj(t)=[Δx(t)sinφj(t)+Δy(t)cosφj(t)]g(φj(t))

(1)

式中：

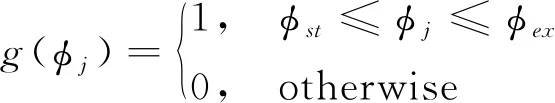
(2)

Δx(t)=x(t)-x(t-T)；Δy(t)=y(t)-y(t-T)；T是兩齒之間的切削間隔時間;φst和φex分別是刀具的切入角與切出角。

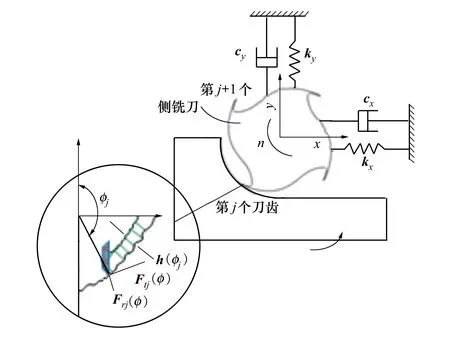
圖1 側銑加工過程的動態模型

X,Y向的切削力可以表示為[24]

(3)

式中：

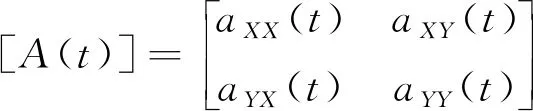
(4)

(5)

式中,KT,KR分別為切向和徑向切削力系數,b為軸向切深。

當刀具旋轉時,方向系數隨著時間而變化。[A(t)]是以刀齒切削頻率(ω(t)=2πnNt/60)為周期的,因此可以展開為傅里葉級數。利用傅里葉級數的平均分量,[A(t)]可以近似表示為[A0][24]

(6)

其中積分函數可以表示為[24]

(7)

動態銑削公式(3)可以簡化為[24]

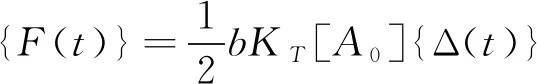
(8)

1.2 顫振穩定性葉瓣圖

刀具-工件接觸區域的傳遞函數矩陣可以表示為[24]

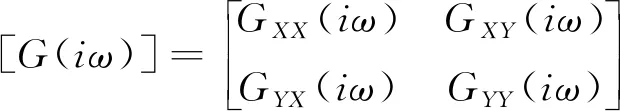
(9)

對于單自由度銑削系統,無顫振時極限軸向切深可以表示為[24]

(10)

式中:ωc為給定顫振頻率,mX、kX、cX分別為X向的模態質量、模態剛度和模態阻尼。

對于二自由度銑削系統,無顫振極限軸向切深可以表示為[24]

dlim=

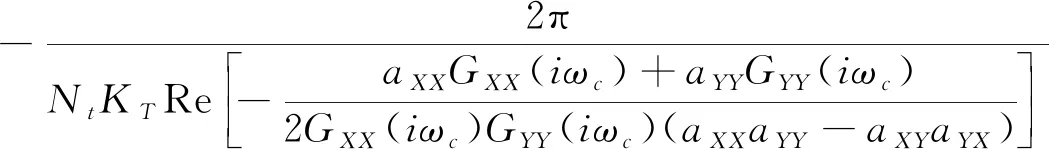
(11)

式中:

(12)

(13)

2 銑削顫振可靠性模型

將銑削加工系統的極限狀態作為臨界穩定狀態。“失效”表示不穩定的加工狀態,刀具的振動隨著切削力無限地增加。“可靠”表示穩定的加工狀態,刀具的振動會在阻尼作用下減弱。

銑削過程中刀具和工件的相互作用產生顫振。顫振頻率與結構參數有關。銑刀的結構參數m,c,k和主軸轉速S是銑削系統基本的隨機變量。

考慮顫振的銑削系統極限狀態函數可以表示為[25-26]

fX(X)=dlim-d

(14)

動態銑削過程的可靠性是在給定的時間和參數下不發生顫振的概率,該可靠性可以定義為[25]

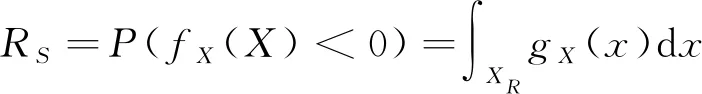
(15)

式中:X為隨機變量向量,X=(m,c,k,ωc);結構參數m,c,k是獨立的變量且服從正態分布;顫振頻率ωc與m,c,k相關,它的分布規律與隨機變量m,c,k和S有關。

3 一次二階矩法

一次二階矩法將失效面泰勒展開點的性能函數線性化。下面將介紹基于一次二階矩法的銑削系統可靠性評估方法。

銑削系統的極限狀態函數為[25]

Z=fX(X)=0

(16)

對于一個二自由度銑削系統,基本的隨機變量X=(x1,x2…xi)T是不相關的,且服從正態分布,其中xi分別為mX,mY,cX,cY,kX,kY和ωc。顫振頻率ωc與mX,mY,cX,cY,kX,kY相關。銑削系統的相關矩陣可以表示為

(17)

式中:ρxixj是變量xi和xj的相關系數。

標準偏差ζmX,ζmY,ζcX,ζcY,ζkX,ζkY,ζSc分別用ζ1,ζ2,ζ3,ζ4,ζ5,ζ6,ζ7表示。 銑削系統的協方差矩陣為

(18)

矩陣D是7階正定對稱矩陣。該矩陣有7個實特征值和7個線性無關的正交特征向量。

矩陣B的列向量由矩陣D的正則化特征向量構成。對銑削系統的隨機向量X做正交變換[25]

X=BY

(19)

μY=BTμX

(20)

ζY=BTζX

(21)

極限狀態函數可以表示為獨立隨機變量Y的函數[25]

Z=fX(X)=fX(BY)=fY(Y)

(22)

基于設計點法,變量Y的導數為[25]

(23)

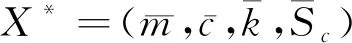
Y*=BTμX

(24)

在空間Y中,Z=0是通過點Y*的極限狀態切平面。根據獨立隨機變量線性組合的性質,可以得到Z的均值和標準差[25]

(25)

(26)

銑削系統的可靠性指標為[25]

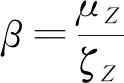
(27)

定義變量Yi的敏感度系數為[25]

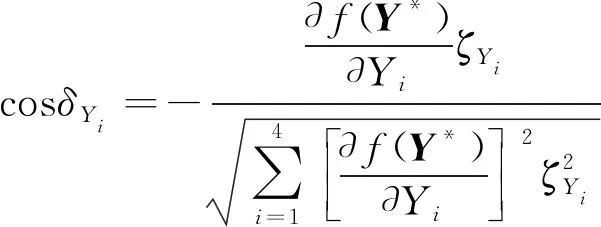
(28)

新Y*可以表示為[25]

Y*=μYi+βζYicosδYi

(29)

新X*可以表示為[25]

X*=BY*

(30)

設置誤差為ε=10-6, 一直迭代直到2次迭代的偏差小于ε。將β值代入公式(29)可計算得到Y*的值。

銑削系統的可靠性概率定義為[25]

pr=1-Φ(-β)

(31)

式中，Φ(·)是標準正態分布的累積函數。

該工程區的大地構造單元為長江三角洲褶皺帶中的景潭斑塊褶皺束，由前震旦系變質巖組成。隧道的邊坡坡度陡，地形陡峭。隧道位于地形的陡峭交交匯處。邊坡圍巖發育一組外部斜坡接頭，在外部接縫面應力進行了重新分布并伴隨著剪切位移及卸荷裂縫。邊坡圍巖地貌照片見圖1。邊坡圍巖有一組外傾節理發育，沿節理面發生了應力剪切錯動，并伴著應力重分布及卸荷裂隙。邊坡主要軟弱結構面發育照片見圖2。隧道設計的本段圍巖等級為Ⅴ級，支護類型為錨網噴護加鋼拱架，斷面結構類型為半明半暗，開挖方式為全斷面，見圖3。

4 應 用

4.1 整體葉盤側銑加工實驗

實驗在五軸加工中心上進行。利用模態沖擊錘(PCB 086C03)、加速度傳感器(Kistler 8778A500)、振動信號采集卡(NI 9233)和分析軟件(Cutpro V9.0)完成側銑加工系統模態參數的識別,如圖2所示。

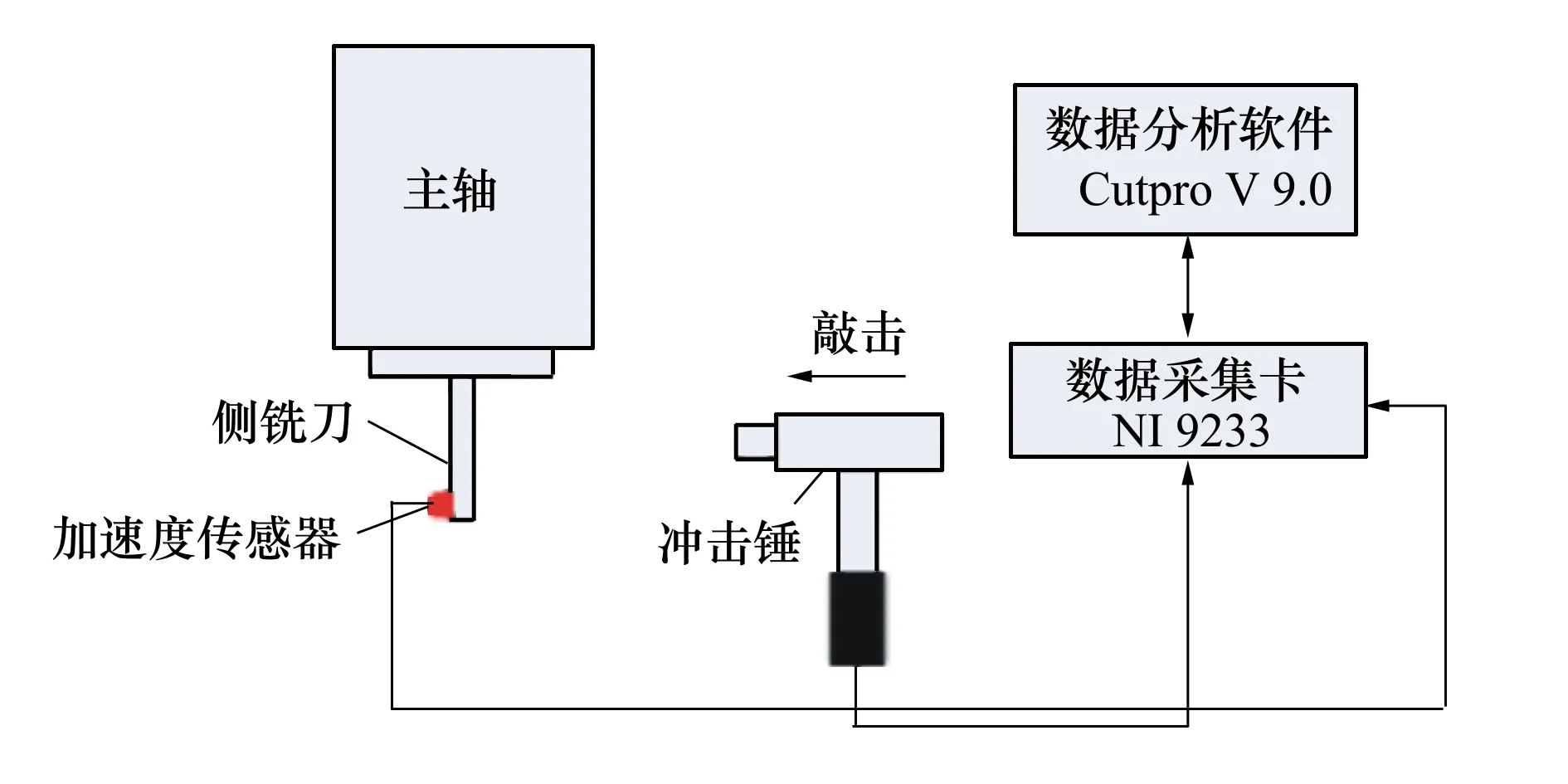
圖2 振動信號采集過程

模態實驗沿著側銑刀的X和Y向進行。X,Y向的頻響函數如圖3和4所示。表1和2列出了X,Y向模態參數的多次實驗測量結果。側銑加工系統結構參數平均值和標準差計算結果如表3所示[27-28]。

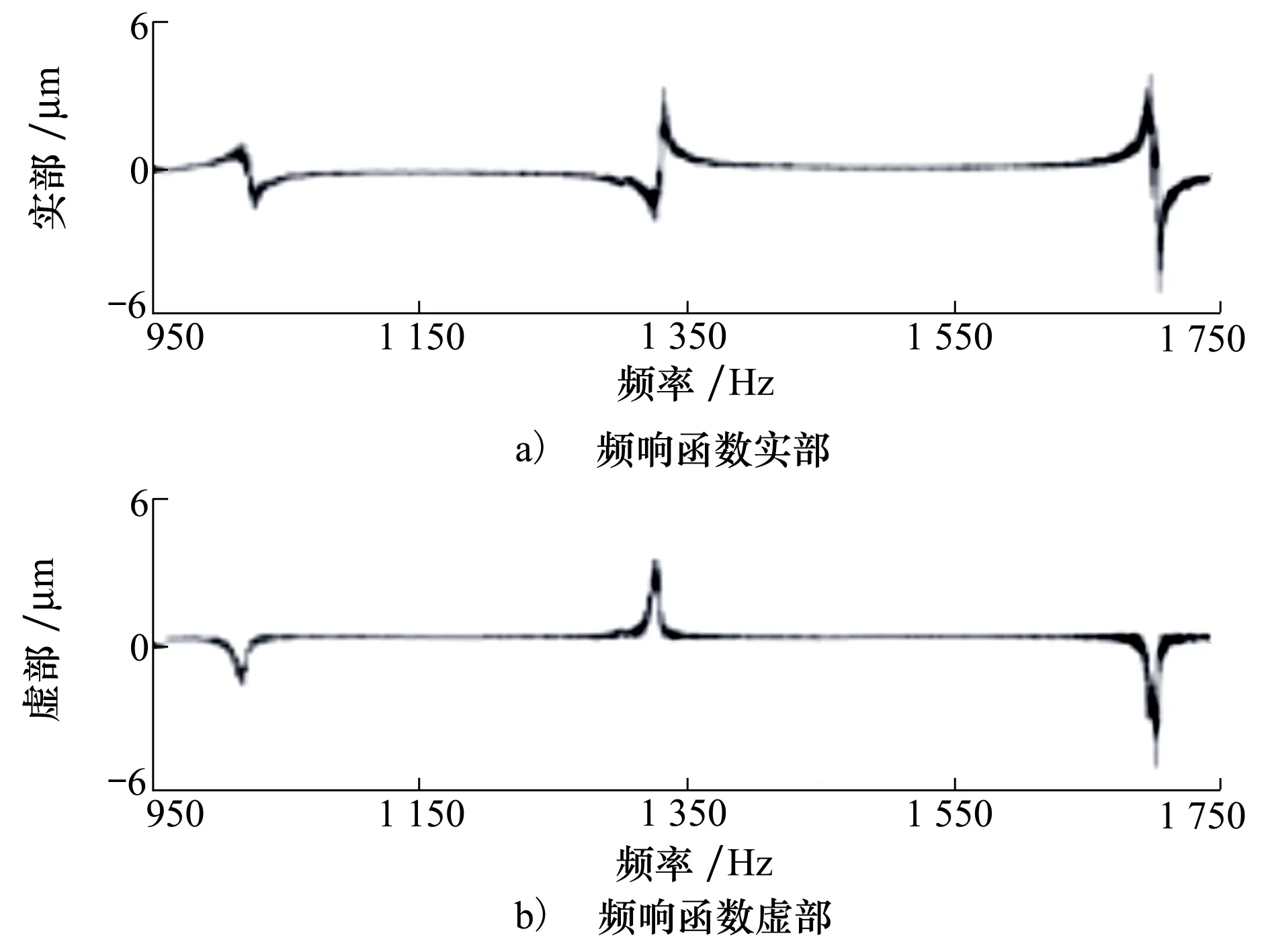
圖3 側銑刀X向頻響函數

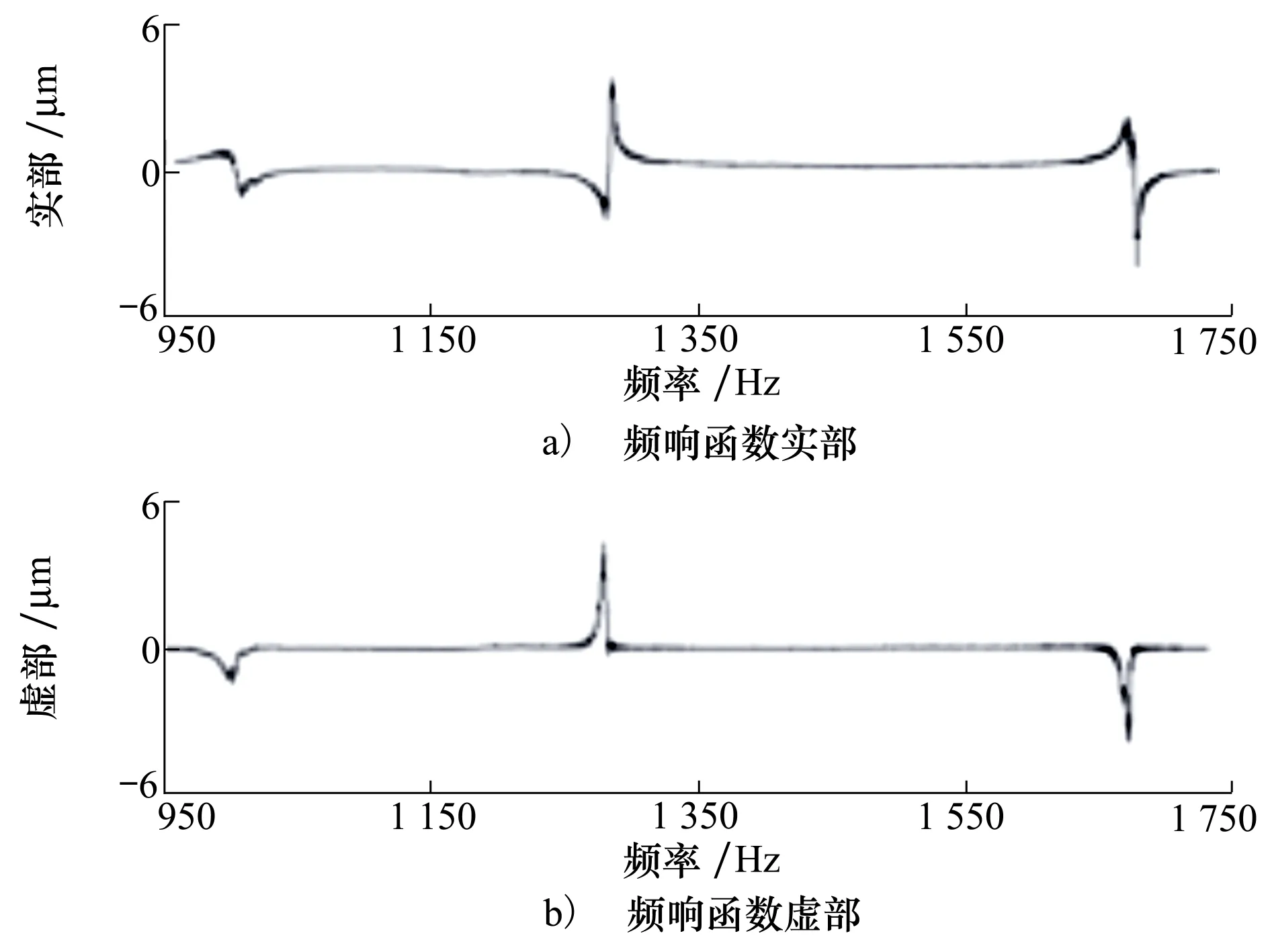
圖4 側銑刀Y向頻響函數

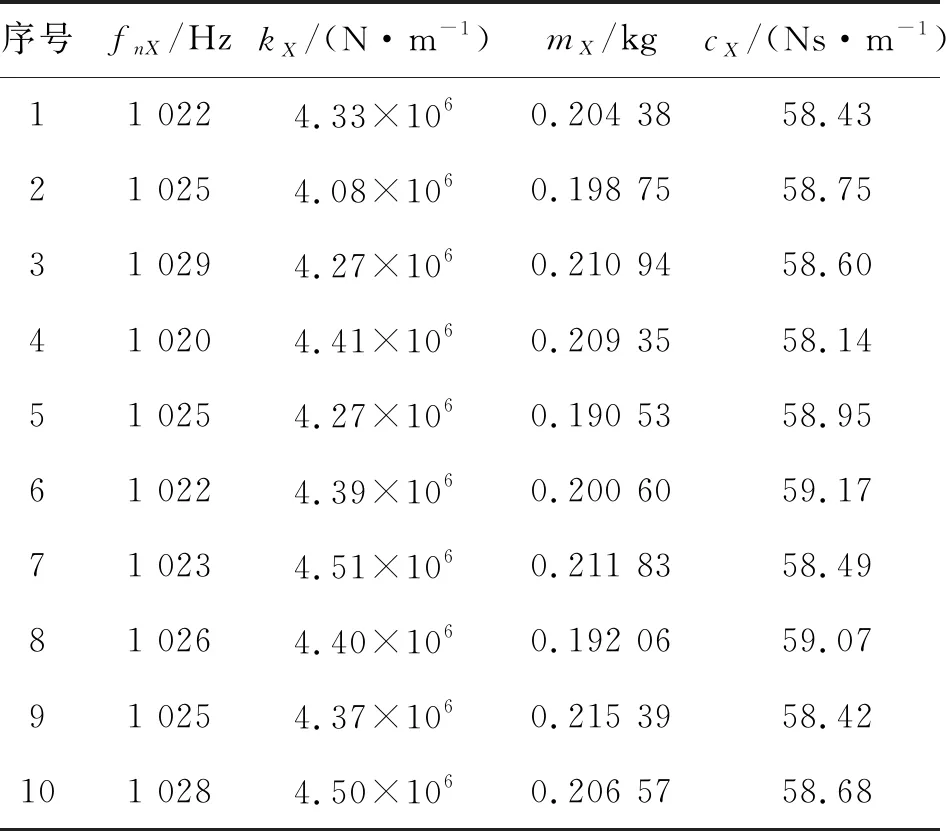
表1 側銑刀X向模態參數測量值

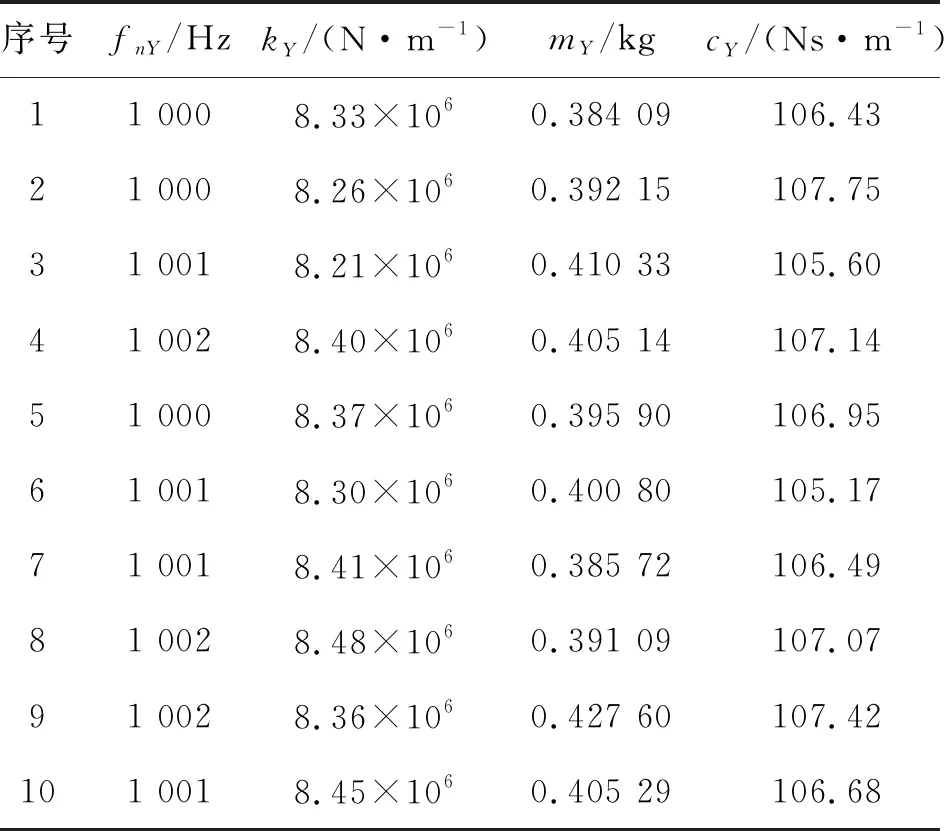
表2 側銑刀Y向模態參數測量值

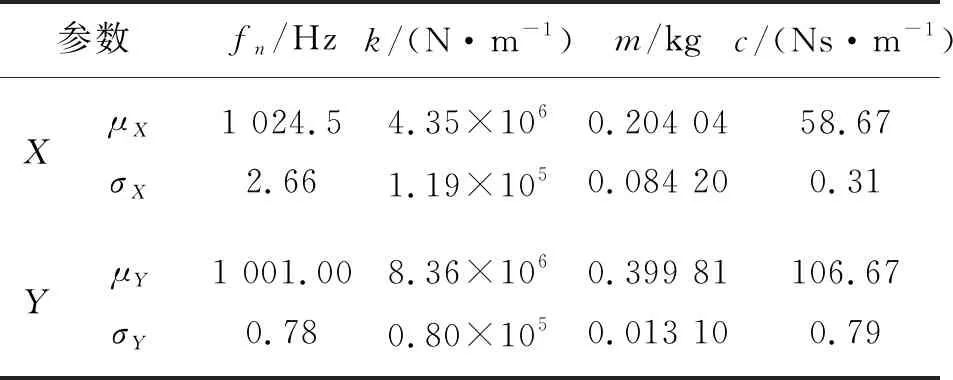
表3 側銑刀模態參數平均值及標準差

4.2 側銑顫振頻率的分布

對于二自由度的側銑加工系統,結構參數mX,mY,cX,cY,kX,kY取為實驗測量結果的平均值。圖5給出了側銑加工系統的穩定性葉瓣圖和顫振頻率圖,穩定性葉瓣圖如黑色實線所示,顫振頻率隨主軸轉速變化圖如圖藍色點線所示。

圖5 側銑加工系統穩定性葉瓣圖與顫振頻率圖

4.3 側銑加工系統的可靠度計算

側銑加工系統穩定運行條件必須滿足fX(X)<0。當已知切削深度時,側銑加工系統的可靠度可由一次二階矩法[24,26]和蒙特卡羅法得到。初始點設為側銑加工系統隨機變量平均值。一次二階矩法和蒙特卡羅法得到的可靠度比較結果如表4所示。結果表明,一次二階矩法的計算結果與蒙特卡羅法的計算結果吻合較好。相對誤差最大的是7.43%。因此,一次二階矩法可以應用于側銑加工系統顫振可靠度的計算。

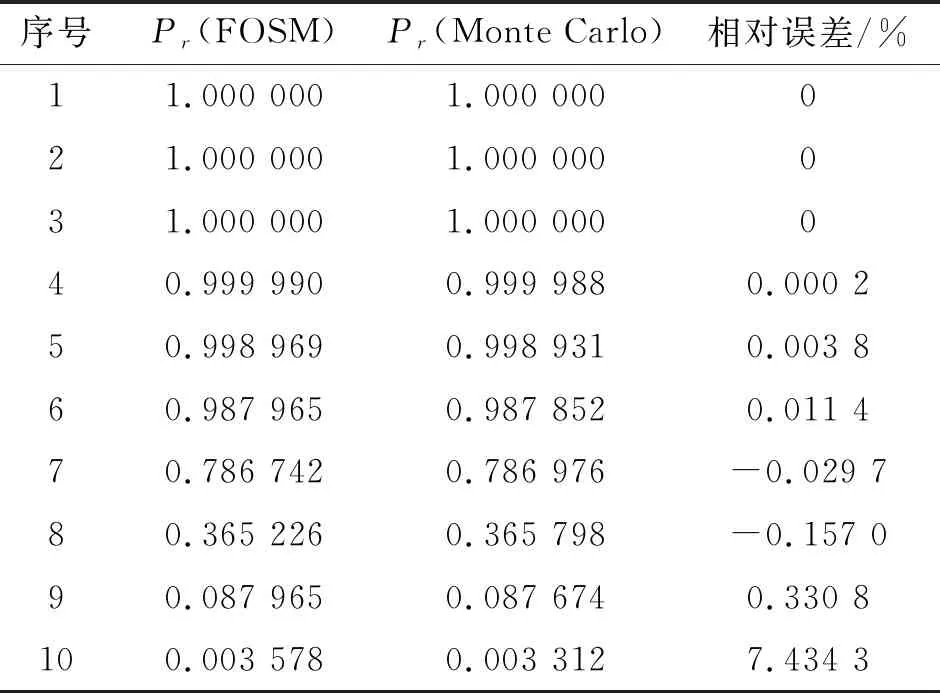
表4 給定切削深度主軸轉速6 000 r/min的可靠度

4.4 可靠性葉瓣圖

可靠度值設置為0.99。可靠性葉瓣圖與穩定性葉瓣圖對比如圖6所示,黑色實線為穩定性葉瓣圖,藍色虛線為可靠性葉瓣圖。藍色虛線下方是可靠區域,可靠度大于0.99,藍色虛線上方是不可靠區域,可靠度小于0.99。黑色實線下方與藍色虛線上方的區域是穩定但不可靠區域,可靠度小于0.99。藍色虛線下方的區域是即穩定又可靠的區域,可靠性大于0.99。黑色實線上方的區域是即不穩定也不可靠區域,可靠性小于0.99。

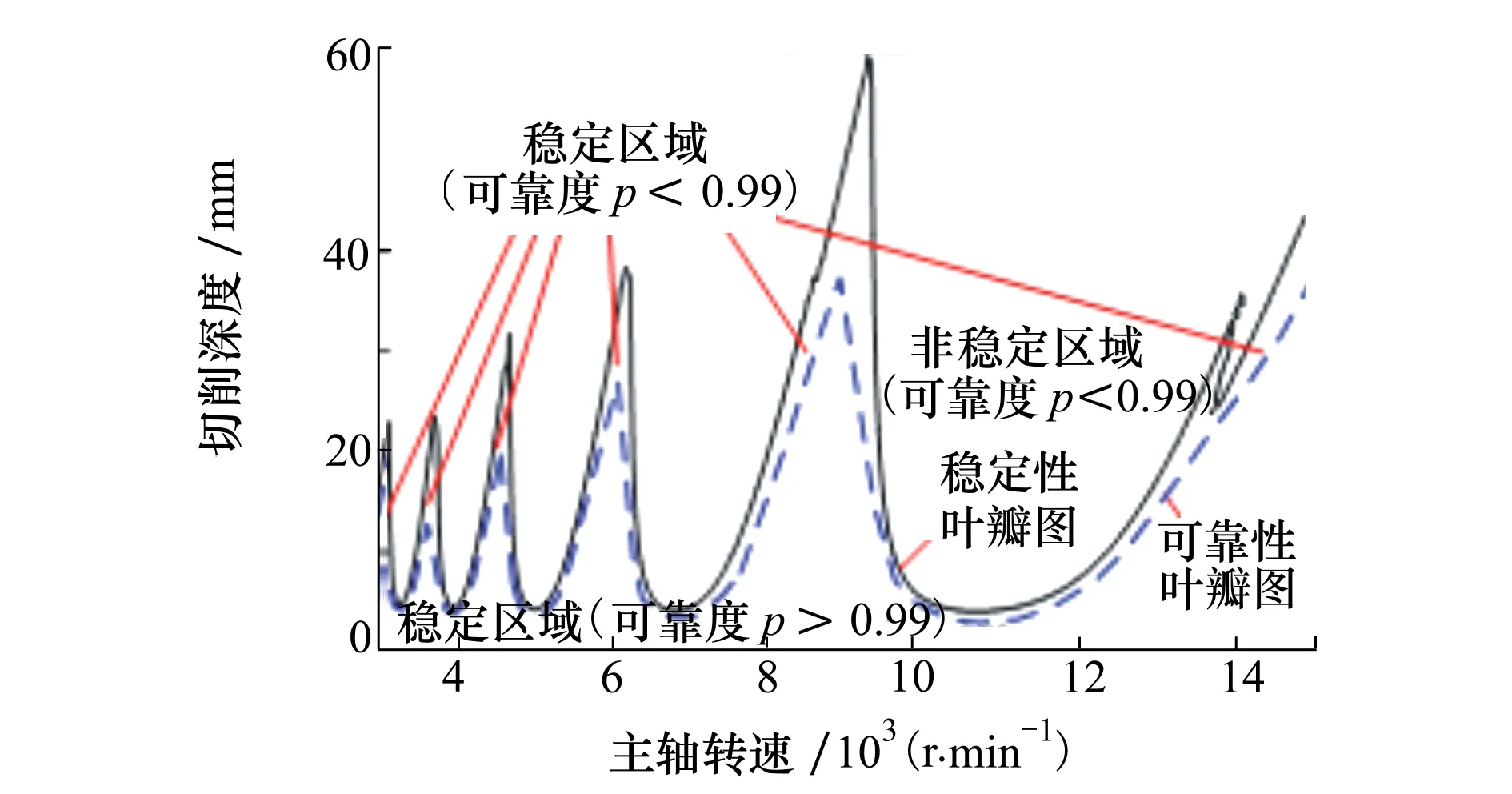
圖6 側銑加工系統穩定性與可靠性葉瓣圖對比圖

4.5 實驗驗證

側銑驗證實驗在五軸加工中心上進行,主軸轉速設置為6 000,8 000和14 000 r/min。切削深度為10～60 mm。當主軸轉速為6 000 r/min,切削深度為20 mm時,加工表面光滑,可靠度值為0.999 86。當主軸轉速為8 000 r/min,切削深度為20 mm時,加工表面呈波紋狀,如圖7所示,可靠度值趨近于0。

在可靠性葉瓣圖上得到了關鍵可靠性值和極限可靠性值,如圖8中的黑色圓點所示。當主軸轉速為6 000 r/min,切削深度為26.6 mm時,可靠度為0.99,切削深度繼續增加時,可靠度值下降,直到發生顫振,可靠度為零;當主軸轉速為15 000 r/min,切削深度為36.8 mm時,可靠度為0.99,隨著切削深度的增加,可靠度值會一直下降到零。驗證實驗的結果在圖8中標出,五角形代表穩定點即無顫振發生,三角形代表不穩定點即發生顫振。實驗結果與預測結果保持一致。實驗結果表明可靠性葉瓣圖可用于預測側銑加工系統的穩定性概率。

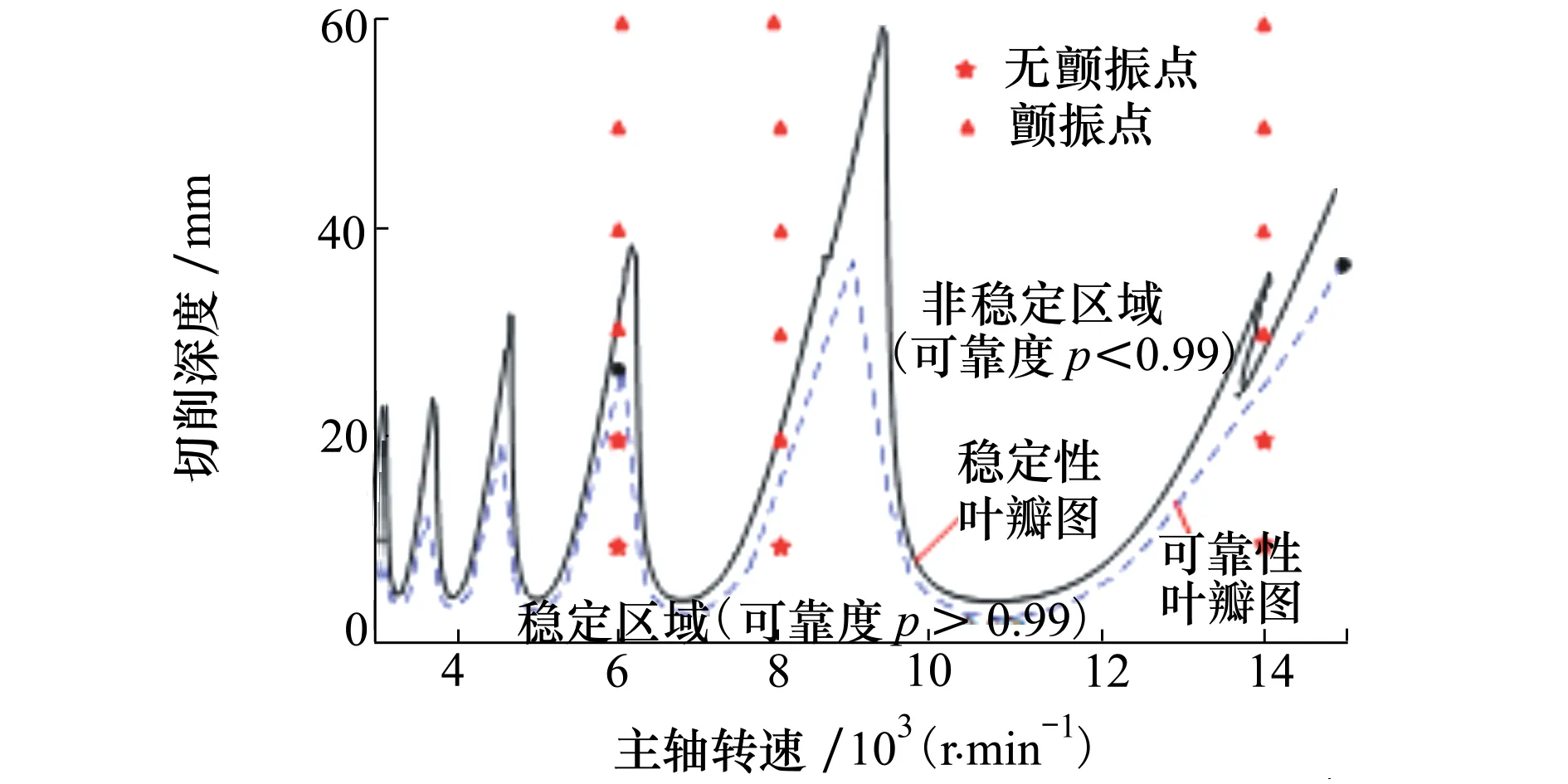
圖8 驗證實驗結果

5 結 論

本文建立了考慮隨機變量影響的側銑加工系統顫振可靠性預測模型。通過模態實驗獲得了側銑加工系統X向和Y向的結構參數。利用結構參數的平均值繪制了側銑加工系統的穩定性葉瓣圖和顫振頻率圖。利用一次二階矩法計算了側銑加工系統的可靠性指標和可靠性概率,并與模特卡羅法的計算結果進行了對比。利用可靠性葉瓣圖對側銑加工系統的顫振區域與非顫振區域進行識別。可以得出以下結論:

1) 顫振頻率是一個隨機變量,它與結構參數m,c,k和主軸轉速S有關;

2) 用一次二階矩法和蒙特卡羅法對側銑加工系統的可靠性概率計算結果具有較高的一致性。利用一次二階矩法可以計算側銑系統的可靠性概率。

3) 可靠性葉瓣圖可較好地預測側銑加工系統的顫振可靠性;可靠性葉瓣圖可用于側銑加工系統的穩定性概率估計。