探究“新零銷售”模式下影響銷售量的相關因素

衛俊峰 沈喬羽 常瑩杰

【摘? 要】在新零銷售模式的推動下，客戶越來越傾向于消費個性化的商品。為了精準預測客戶的消費需求，論文以單款單色產品為研究對象，通過建立多元回歸分析的數學模型，來探究影響商品銷售量的相關因素。經過分析發現，除了一些定性因素外，定量因素對銷售量也產生了一定的影響，其中實際花費總金額、實際銷售單價、庫存數等定量因素對銷售量的影響較大，且各個變量之間具有相關性，所以電商平臺應特別關注這三個變量的影響。

【Abstract】Drived by the new retail mode， customers are more and more inclined to consume personalized goods. In order to accurately predict the consumer demand of customers， this paper takes a single monochrome product as the research object， and explores the related factors that affect the sales volume of the product by establishing a mathematical model of multiple regression analysis. Through analysis， it is found that in addition to some qualitative factors， quantitative factors also have a certain impact on the sales volume. Among them， quantitative factors such as actual total amount spent， actual sales unit price and inventory number have a great impact on sales volume， and each variable is correlated. Therefore， e-commerce platforms should pay special attention to the impact of these three variables.

【關鍵詞】銷售量;多元回歸分析;相關性;假設檢驗;影響因素

【Keywords】sales volume; multiple regression analysis; correlation; hypothesis testing; influencing factors

【中圖分類號】F274? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 【文獻標志碼】A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文章編號】1673-1069（2021）01-0147-03

1 引言

當今時代，互聯網發展日益迅猛，大數據的廣泛應用為分析消費者的需求帶來了極大的便利，在數據挖掘的推動下，新零銷售模式下的電商平臺將消費信息轉化為數據，將數據轉化為知識，最后再用知識為商家的決策和行動提供指導。

現如今，國內外已經有許多專家學者對銷售量的影響因素進行了研究，例如，滕樹軍、鄭惠文和劉柏森三人用多元回歸的方法對超市商品的銷售進行了分析[1]。黃曉梅建立了一元線性回歸方程來預測飲料的銷售量[2]。Doganis采用了非線性時間序列并融合了遺傳算法的徑向基神經網絡構成建立了中期銷售量預測模型[3]。

對比上述的研究方法，本文利用新零銷售模式非常重要的商業優勢和資源，將掌握的龐大的消費數據存貯起來，結合數據挖掘技術采集所需要的消費數據并提取合適的影響因素，本文用到的影響因素包括銷售量、銷售單價、銷售金額、庫存數、標簽價和折扣，之后對這些因素進行分析，建立多元回歸分析的數學模型，得出相應的結論后，為商家提供一個合適的營銷方案。

2 定性因素分析

從20世紀50年代開始，國內外專家就開始研究消費心理，不難發現，沖動性購買[4]是消費心理折射出的一種最主要的行為特征。利用電商網絡平臺進行交易的對象主要是廣大青年群體，他們大多數消費心理不成熟，容易被外界誘導，做出一些不合理的消費行為，因而消費心理影響著青年群眾。

此外，產品的前期宣傳也是一個重要環節，一件商品的宣傳度直接決定了商品在消費中的盈虧情況。在宣傳中，廣告費用所占比重較多，它與銷售提高因子有關，且二者近似呈現二次關系，說明存在一個廣告費的最優值，使得提高因子最大，提高因子與預期銷售單價相乘就是定量因素實際銷售單價[5]，如何科學地支出這筆費用，對銷售量的大小起到了至關重要的作用。

節假日期間，各種打折促銷活動吸引著廣大的消費者，利用微觀經濟數據分析，我們知道客戶在節假日消費時，其價格彈性[6]具有顯著性的變化。國內外一些學者研究指出，節假日期間消費對產品價格的變化具有一定的影響，從而影響消費者的選擇，間接使銷售量產生波動。因此，折扣促銷是節假日期間商家互相競爭的核心策略，把握節假日的消費數據對探究銷售量的影響因素也具有重要意義。

3 數據采集和定量因素提取

3.1 產品銷售數據采集

本文的銷售數據來源于第十屆MathorCup高校數學建模挑戰賽D題中某零售企業生產的N款產品在華東區內的相關數據。

我們采取的數據集包括五大類：第一類包括產品編號、日期、銷售量和實際花費總金額;第二類包括產品編號、產品小類編號、日期和標簽價;第三類包括產品編號、日期和庫存總數;第四類包括產品編號、日期和折扣;由于標簽價與折扣相乘可以得到實際銷售單價，因此我們根據這兩個變量，得到第五類數據，包括產品編號、日期和實際銷售單價。

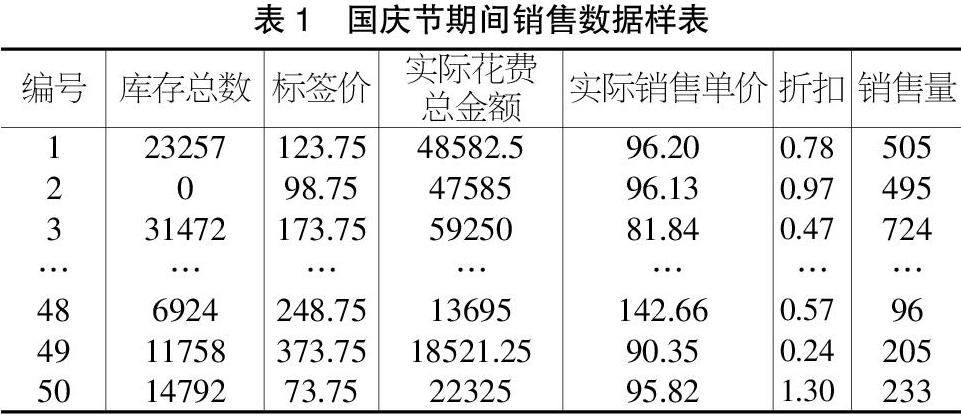
由于我們采集的產品種類有很多，且每種產品在各個時間段中的消費數據都不一樣，所以為了使分析更加簡便，消除數量和日期對變量的影響，我們集中分析國慶節期間產品的銷售情況，并且將該期間內實際花費總金額位列前五十的產品列舉出來，求出這些產品的庫存總數、標簽價、實際銷售單價、折扣和銷售量在國慶節期間內的總和，將其作為觀測數據，得到的數據如表1所示。

3.2 產品定量影響因素的提取

本題研究的對象是目標區域內商品的銷售量，要求我們分析各種相關因素對商品銷售量的影響。傳統的性價比等因素已經不能為分析“新零售”模式下商品的銷售量提供可靠性的依據，所以，在研究其他因素對銷售量的影響時，我們需要引進新的變量，本文我們著重分析庫存總數、標簽價、實際花費總金額、實際銷售單價和折扣對商品銷售量的影響。

4 模型建立與模型求解

4.1 模型假設

①考慮到定性因素無法用精準的數據來表示，這里我們假設定性因素不構成數值上的影響。②假設定性因素對定量因素的影響較小，在進行回歸分析中，我們對其不予討論。③假設除了以上因素對銷售量具有影響之外，其余因素的影響都包含在隨機誤差中，且隨機誤差服從正態分布。

4.2 變量假設

設銷售量為y，庫存總數為x1、標簽價為x2、實際花費總金額為x3、實際銷售單價為x4、折扣為x5，由于折扣與標簽價相乘就是實際銷售單價，所以得到x4=x2x5，因此我們僅利用x1、x3、x4來建立y的回歸方程，我們稱庫存總數、實際花費總金額、實際銷售單價為自變量，也稱為回歸變量，y是給定的因變量，其中我們設β1、β3、β4是相應自變量的回歸系數，β0為常數，隨機誤差為δ。

4.3 模型求解

4.3.1 相關性分析

在建立回歸方程之前我們需要先進行相關性分析，通過求出的斯皮爾曼相關系數來判斷所設的自變量是否和因變量有明顯的關系，如果關系較大，我們將繼續建立回歸方程，如果關系不明顯，則需要重新考慮新的自變量。為使斯皮爾曼相關系數合理，我們還需要通過假設檢驗的方法來驗證。在本次數據中，樣本量n≤50，統計量r～N（0，1），首先用SPSS求得斯皮爾曼相關系數如表2所示。

緊接著我們用假設檢驗來驗證相關系數是否合理，假設H0：r=0在95%的置信水平下成立，H1：r≠0在5%的顯著水平成立，從上述的操作結果來看，P值都為0.000，證明各個相關系數在5%的顯著水平下已經成立，說明相關系數結果可以接納，而且各個相關系數|r|>0.6，可以證明銷售量與庫存總數、實際花費總金額、實際銷售單價之間的相關性較大。

4.3.2 回歸分析

最小二乘法是一種數學優化技術。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小。在知道了因變量與各個自變量之間具有相關性以后，我們先建立多元線性回歸方程，然后通過觀察擬合優度來判斷線性方程的可行性：

y=β0+β1x1+β3x3+β4x4+δ

并且用Stata求解上述回歸方程的回歸系數，得到的相關結果如表3所示。

我們從表中可知，擬合優度的值都十分接近1，因此說明了x1、x3、x4對呈明顯的線性關系，即我們上述建立的線性回歸方程是可行的。

但庫存總數的P值為0.163，大于0.05，即小于95%，假設H0：回歸系數不顯著異于0。H1：回歸系數顯著異于0，系統默認H0：的概率為95%，則我們接受原假設H0，認為庫存總數的回歸系數等同于0，我們之前分析相關性的時候得出庫存總數與銷售量存在著顯著的相關性，這與P=0.163相矛盾，因此說明我們建立的回歸方程雖是線性的，但還需要改進，改進的方法是給方程加一個新的變量以此降低庫存總數的P值。

4.3.3 模型優化

經過分析，我們發現庫存總數與實際銷售單價有一定的關系，設x6=x1x4。優化模型：

y=β0+β1x1+β3x3+β4x4+β6x6+δ

再用Stata求解優化后回歸方程的回歸系數，得到的結果如表4所示。

對優化后的模型，擬合優度比之前更加接近于1，則我們可以認為因變量對自變量的線性關系更強了，且P值均小于0.05，所以認為庫存總數的回歸系數顯著異于0。

方差膨脹因子VIF是用來檢驗相關因素之間的多重共線性，某個自變量的VIF值越大，說明該自變量與其他自變量的相關性越大，一般我們認為VIF大于10時，方程存在嚴重的多重共線性，如果小于10時，則可以不考慮方程的多重共線性。

我們從該表中可知VIF的值均小于10，則認為庫存總數、實際花費總金額、實際銷售單價之間沒有多大關系。

4.3.4? 隨機誤差分析

最后，對于隨機誤差δ，在檢驗的時候，Stata系統默認設原假設H0：不存在隨機誤差，H1：存在隨機誤差，H0：概率默認為95%，通過運行結果來看，P值均小于0.05，即我們拒絕原假設，說明我們優化后的回歸模型存在隨機誤差。

標準化后的隨機誤差在各自穩健的標準誤差最大區間內滿足T統計量分布同時也滿足正態分布，P值均小于0.05，設H0：不能消除隨機誤差的影響，默認其概率為95%，H1：可以消除隨機誤差的影響，證明超過95%的概率可以接受H1，即所求的回歸系數在誤差之內可以接受。根據上面的回歸分析結果，可建立最終的回歸方程：

y=69.90238+0.0138958x1+0.0101904x3-0.7307054x4-0.0001325x1x4

5 模型評價與結論

5.1 評價

5.1.1 優點

在最開始，我們發現銷售單價、標簽價和折扣之間的關系，為了使分析更加簡便，則用銷售單價代替了標簽價和折扣，后面進行回歸分析時就可以不用再考慮這三個變量之間的多重共線性。在建立回歸方程之前，我們檢驗了變量之間的相關性，為后來的回歸分析消除了無關變量的影響，同時擬合優度證明出因變量和自變量之間呈現明顯的線性關系，這些操作可以幫助我們更好更快地建立回歸方程的初步模型。在求解回歸系數時，我們對回歸方程也進行了多重共線性分析，這樣做既檢驗了變量之間的相關性，又可以對不足之處進行適當的模型優化，使得回歸方程更加準確合理。最后，我們對隨機誤差進行了檢驗，證明了在誤差之內，所求解的回歸系數及回歸方程的合理性。所有的建模分析過程運用了多種數據統計軟件，操作簡便，邏輯嚴密，結論科學可靠。

5.1.2? 缺陷

我們在分析的過程中發現實際銷售單價并不能完全代替標簽價與折扣的影響，之后我們可能會對這兩個變量單獨進行分析，此外我們研究的變量數目不超過8個，因此實驗結論嚴謹性還有待提高。對于定性因素，我們也盡量用數值來體現出來，我們的模型優化基本只進行了一次，為了實驗更加精準，我們需要不斷優化模型提高擬合度。

5.2 結論

經過分析可知，對銷售量的影響存在著多方面的因素，除了一些定性因素外，銷售單價、銷售花費總金額以及庫存數等定量因素對銷售量的影響較大。

在銷售的過程中，商品的銷售量往往與商品單價成反比關系，商品定價越高，客戶的購買力越低，商品的銷售量越少，而且商品的單價還與庫存數存在著交叉關系，即二者相互影響，共同決定產品的銷售情況。所以商家在制定長期的銷售方案中要著重考慮商品單價。

在銷售之前，商家需要提高供給水平，給予充足的庫存量，以保證商品物流渠道通暢，不會存在通貨膨脹或者通貨緊縮等情況，一般庫存量越高，銷售量也就越高。此外，商品的銷售量還與實際花費總金額成正比關系，且庫存總數對銷售量的影響程度與實際花費總金額對銷售量的影響程度基本相同。

我們要時刻與顧客保持良好的溝通渠道，每個月可對前段時間的銷售業績進行評估，分析影響銷售量的相關因素，更準確地定位到消費者的消費心理，拓寬消費市場，打造自身的專業品牌，以預測未來的市場導向，為店鋪贏得銷售先機，更好地搶占市場。

【參考文獻】

【1】滕樹軍，鄭惠文，劉柏森.基于多元回歸分析的超市商品銷售影響因素的研究[J].全國流通經濟，2018（14）：6-9.

【2】黃曉梅.一元線性回歸分析法在超市產品銷售中的應用[J].科技信息，2013（11）：77-78.

【3】Doganis，P. Alexandridis，A. Patrinos，P. and Sarimveis，H.Time series sales forecasting for short shelf - life food products based on artificial neural networks and evolutionary computing[J].Journal of Food Engineering，2006，75（2）：196-204.

【4】張武康，郭關科.移動購物平臺對大學生沖動性購買意愿的影響分析[J].經濟師，2019（1）：197-198，200.

【5】燕芊宇.基于微分方程的廣告費模型探究[J].價值工程，2020，39（3）：274-276.

【6】李國棟.消費者購買行為的假日效應——基于掃描數據的微觀實證[J].財經論叢，2014（9）：82-89.