鏈接算籌文化　凸顯十進位值制

竺君斐　周潔

“數的認識”板塊的本質內容是十進位值制。十進位值制記數法包括“十進制”與“位值制”兩條原則。“十進”指的是“滿十進一”。“位值”是同一數字在不同位置上所表示的數值不同。如三位數“555”，右邊的5在個位上表示5個一，中間的5在十位上表示5個十，左邊的5在百位上則表示5個百。十進位值制使極為困難的整數表示和驗算變得簡便易行。

怎樣在“認識萬以內數”教學過程中讓學生深度理解“十進位值制”的內涵與價值？常規的做法是：通過數數活動中的“怎樣數”“怎樣記錄”這兩個問題展開。以數黃豆為例，當“捏一撮”（10以內）時，我們可以一個一個地數;當“抓一把”（100以內）時，我們可以十個一堆，十個一堆地數;當數目更大時，就需要用更大的計數單位來記數，進而明確一而十，十而百，百而千，千而萬。記錄黃豆數量的同時，需要明確每一個數位上數的含義。

很多“認識萬以內數”教學設計能從數的本質出發，讓學生在活動中體會十進位值制的含義，以及計數單位之間的關系。但是，學生對其中“滿十進一”體會深刻，對位值制的價值卻感悟不深。

十進位值制是我國最早發明的。文明古國巴比倫采用60進位制（這一進位制到現在仍留有痕跡，如1分=60秒）。古印度、古埃及也很早就采用了十進位制，但是他們沒有位置，沒有零，并不知道位值制。如古埃及采用“計算單位累加”的方法，不同計算單位用不同的符號表示，從圖1古埃及的“235”中可以看到2個百用2個“旋風”，3個十用3個“門洞”，5個一用5個小棒表示。依次推理。如果表示999，“旋風”“門洞”“小棒”分別要畫9個，非常繁瑣，給記錄與運算帶來不便。

從歷史發展順序來看，“位值”的出現明顯比“十進”晚，說明“位值”比“十進”更難理解。

弗賴登塔爾認為：“年輕的學習者應重蹈人類的學習過程。”列寧也曾經說過：“一門科學的歷史是那門科學中最寶貴的一部分，科學只能給我們知識，而歷史卻能給我們智慧”。數學，既是被人們發現的，也是被人們創造的。前人在數學研究過程中，其數學思維和經驗教訓是非常有借鑒意義的，對小學生的數學思維能力有著極大的促進作用。

因此，“認識萬以內數”一課，有必要鏈接教材“你知道嗎”板塊中的“算籌文化”，讓學生在“中國算籌”“古埃及記數法”兩種記數方法的認識、試寫、對比中，挖掘“十進位值制”背后的數學思想與方法，讓學生充分感受“位值制”的簡潔與價值，豐滿數學教學中的“人文元素”，體會“數學有著悠久的鮮活的歷史”。

一、靜態的中國算籌：動態評價中體會“古人智慧”

教材呈現的知識是靜態的。而站在歷史的角度，動態地看待數學知識產生和發展過程，了解數學發展的歷史，參與再創造，有利于學生感受數學知識靈動的一面。

中國算籌一般是用小竹棍（或其他材料）制成。古人為了區分相鄰數位上的數，創造了橫向、縱向兩種算籌。需要學生體驗這個動態發生過程。

第一步，借助方塊直觀模型，理解數位意義。

（1）課件有序出示小方塊（1個、10個、100個、1000個），明確計數單位個、十、百、千。

（2）課件出示235個小方塊。明確235由幾個百、幾個十、幾個一組成。

（3）指一指：這個“2”表示圖上哪些小方塊？

（4）追問：為什么它可以表示這么多方塊？因為2在百位上，表示2個百。

（4）歸納：個位、十位、百位、千位就是數位。

第二步，介紹中國算籌。

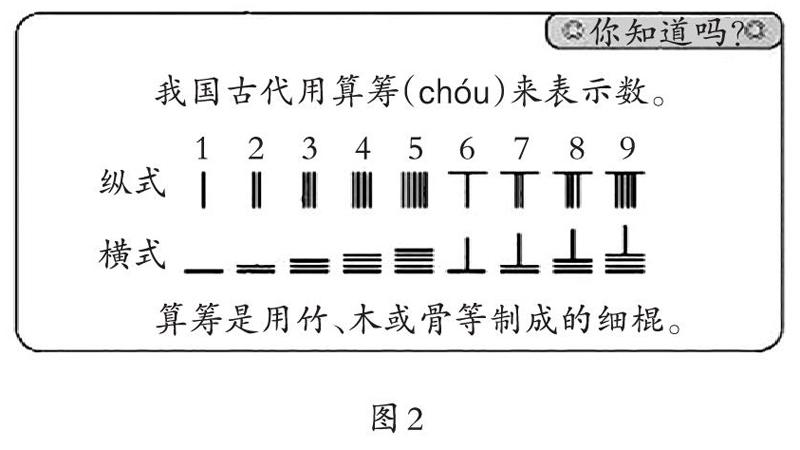
（1）出示“你知道嗎”內容，介紹算籌，了解橫式與縱式兩種表示方法。（如圖2）

（2）追問：“5”用5根小棒表示，為什么“6”不是6根，而用一橫一豎來表示呢？

第三步，用算籌表示235，探究并發現記數規律。

（1）學生嘗試。（如圖3）

（2）交流評價。你喜歡哪一副作品，為什么？

3號作品是正確的。表揚4號作品：“雖然反了，但是他這種縱橫交替的思想特別寶貴。”

第四步，用算籌表示5555。

（1）學生嘗試。

（2）作品反饋。（如圖4）

用算籌表示數，匯集了兩千多年前中國古人的集體智慧。讓學生通過觀察，引發思考，如“6”為什么用一橫一豎表示？因為“以一當五”更簡約更美觀，展現了中國古人的智慧。又如算籌表示235，學生1號作品，容易與55，或者10產生混淆。為了區分2、3、5這三個數字在不同的數位上，中國古人發明并規定個位縱向，十位橫向，交替重復的方法。讓學生在嘗試創造、相互評價中感受其奧妙，發展思維，提升素養。

二、繁瑣的古埃及記數：探究中體驗“機械呆板”

十進位值制之所以被馬克思稱頌為“人類最美妙的發明之一”，是因為它的簡約。萬以內數的認識，除了讓學生掌握位值制的含義，即“相同的數字，在不同的數位上，表示不同的數值”之外，有必要繼續深入探究，體會它的優點。為此，借助古埃及記數“5555”的繁瑣，可以使學生在探究中體驗其方法的呆板。

第一步，介紹古埃及1～9，10，100，1000，10000的表示方法。（如圖5）

第二步，介紹古埃及的“235”，說說他們的記數方法。

第三步，學生獨立探究古埃及“5555”的寫法。

第四步，交流評價學生作品，明確各部分的含義。（如圖6）

學生喜歡創造，喜歡探究。古埃及記數，先舉例呈現，再發現規律，最后讓學生用自己發現的規律試寫“5555”。古埃及計數單位“個、十、百、千”有不同的符號，每個符號需要重復畫5次，用學生的話來說“手都畫酸了”。隨著數量增大，古埃及需要統一更多的計數單位，畫更多次數“小花”“門洞”等，“手就更酸了”。整個過程都以學生為主體，既拓展學生視野，滿足學生探究未知領域的愿望，又訓練學生的思維能力，同時還讓學生深刻體會到古埃及記數方法的繁瑣與復雜，以及記數方法歷史的“豐富性”。

三、中國算籌的位置制：對比中凸顯“高明美妙”

同樣是二千多年前，同樣是“5555”，中國算籌卻與古埃及不同。中國算籌中沒有“小花”“”旋風“門洞”等這些專門的記數符號，只需把算籌“5根小棒”放在不同的數位上，就可以表示5個千，5個百，5個十，5個一了。學生在對比中，對萬以內數的兩種表示方法進行抽象概括，強烈感受到了位值制的高明與美妙，深刻體會中國古人的智慧與偉大創造。

第一步，對比古代中國算籌和古埃及記數法。

師：對比二千多年前古埃及的5555，與古代中國5555，你想說些什么？

生：古埃及的千、百、十、一有專門的符號，中國的算籌沒有專門的符號，用不同數位加以區分。

生：古埃及的太麻煩，我們古代中國的算籌更方便。

生：我們中國人要比古埃及人聰明。用不同數位的數表示不同的計算單位。

生：作為中國人，我很驕傲，我們的祖先太聰明了！

第二步，對比古代中國算籌和現代記數法。

生：現代記數法采用了我國古人發明的“十進位值制”。

生：現代記數法用阿拉伯數字代替算籌1～9，更簡約更方便。

師：數學追求簡潔美，我們現代人使用的萬以內數表示方法凝聚了一代又一代數學家的努力和智慧。“十進位值制”是古代中國人對世界數學發展作出的一項不可磨滅的貢獻。

第一次對比，體會中國算籌位值制的簡約，滲透愛國主義教育。第二次“古代算籌與現代記數法”對比，讓學生感悟到“知識是發展的”“數學是人類共同的文化活動”，而古今中外一代又一代數學家創造精神的傳承，有利于促進學生良好品格的形成，可謂一舉多得。

華東師師范大學的汪曉勤教授曾將HPM研究價值歸納為“知識之諧”“方法之美”“探究之樂”“能力之助”“文化之魅”“德育之效”。以上設計中這六大價值均有所體現。如了解算籌的記數方法，體會“以一當五”，這是感受“知識之諧”;讓學生嘗試探究“中國古人記數235”“古埃及記數5555”，體悟的是數學“探究之樂”;經歷“再創造”的過程，明白縱橫交替擺法的優勢，加強思維訓練，提高解決問題能力，發揮學生能動性，是“能力之助”;在古代中國算籌和古埃及記數方法對比中，感受古埃及記數方法的繁雜，體會中國算籌十進位值制的價值，感受古代中國人民的偉大，是“德育之效”;在歷史發展進程中，感受數學是不斷發展，不斷前進的，數學是屬于全世界人類的一項文化成果，體會的是“文化之魅”。

將數學文化知識“中國算籌”“古埃及記數”融入“認識萬以內數”課堂教學中，充分體現了趣味性、科學性、有效性、可學性、新穎性。學生學得輕松，學得扎實。

（責任編輯：楊強）