ITER 裝置中等離子體旋轉(zhuǎn)和反饋控制對電阻壁模影響的數(shù)值研究*

曹琦琦 劉悅? 王碩

1) (大連理工大學(xué)物理學(xué)院, 三束材料改性教育部重點(diǎn)實(shí)驗(yàn)室, 大連 116024)

2) (核工業(yè)西南物理研究院, 成都 610041)

在托卡馬克等離子體中, 電阻壁模是非常重要的磁流體不穩(wěn)定性, 特征時(shí)間在毫秒量級.對長時(shí)間穩(wěn)態(tài)運(yùn)行下的先進(jìn)托卡馬克, 電阻壁模限制著聚變裝置的運(yùn)行參數(shù)空間(放電時(shí)間和比壓), 影響經(jīng)濟(jì)效益, 所以研究電阻壁模穩(wěn)定性至關(guān)重要.本文使用MARS 程序, 針對ITER 裝置上9 MA 先進(jìn)運(yùn)行平衡位形, 研究了等離子體旋轉(zhuǎn)和反饋控制對電阻壁模的影響.結(jié)果表明, 在沒有反饋控制時(shí), 當(dāng)比壓參數(shù) C β 取0.7, 等離子體環(huán)向旋轉(zhuǎn)頻率達(dá)到1.1%的阿爾芬頻率時(shí), 可以完全穩(wěn)定電阻壁模; 在等離子體環(huán)向旋轉(zhuǎn)和反饋控制共同作用時(shí), 比壓參數(shù) C β 取0.7, 反饋增益 | G| 取0.6 時(shí), 穩(wěn)定電阻壁模所需要的等離子體旋轉(zhuǎn)頻率為0.2%的阿爾芬頻率.可見, 單獨(dú)靠等離子體環(huán)向旋轉(zhuǎn)穩(wěn)定電阻壁模所需的旋轉(zhuǎn)頻率較大; 而等離子體環(huán)向旋轉(zhuǎn)和反饋控制共同作用可以降低穩(wěn)定電阻壁模的旋轉(zhuǎn)頻率臨界值, 符合先進(jìn)托卡馬克的運(yùn)行.本文的研究結(jié)果對中國聚變工程試驗(yàn)堆CFETR 的工程設(shè)計(jì)和運(yùn)行具有一定指導(dǎo)意義.

1 引 言

托卡馬克實(shí)驗(yàn)中可以通過提高裝置的比壓來實(shí)現(xiàn)聚變功率和自舉電流份額的提升.而隨著裝置比壓的增加, 由壓強(qiáng)或壓強(qiáng)梯度驅(qū)動的磁流體不穩(wěn)定性可能會出現(xiàn), 外扭曲模是其中最重要的磁流體不穩(wěn)定性之一.外扭曲模對托卡馬克裝置放電產(chǎn)生重大影響, 嚴(yán)重時(shí)甚至直接導(dǎo)致放電破裂或終止.早期的研究表明, 當(dāng)托卡馬克等離子體外部有足夠靠近的理想導(dǎo)體壁時(shí), 外扭曲?？梢酝耆环€(wěn)定住.所謂理想導(dǎo)體壁是指電阻為零的導(dǎo)體壁.在實(shí)際實(shí)驗(yàn)中, 真空室或第一壁材料等都有一定的電阻, 有電阻的導(dǎo)體壁稱為電阻壁.這類電阻壁使外扭曲模演化為一種增長率緩慢的不穩(wěn)定模式, 由于這種不穩(wěn)定性與電阻壁有關(guān), 被稱為電阻壁模(resistive wall mode, RWM)[1?3].電阻壁模的特征時(shí)間是磁場在電阻壁滲透的特征時(shí)間, 為毫秒量級[4].電阻壁模一旦產(chǎn)生, 仍然會造成等離子體的扭曲, 嚴(yán)重時(shí)也會導(dǎo)致放電破裂.因此, 對于需要長時(shí)間穩(wěn)態(tài)運(yùn)行的先進(jìn)托卡馬克, 電阻壁模的研究是非常重要的.

2004 年Liu 等[5]對ITER 裝置的反饋控制和等離子體環(huán)向旋轉(zhuǎn)穩(wěn)定電阻壁模進(jìn)行了研究, 結(jié)果表明, 安裝在真空室內(nèi)的線圈和極向傳感器組成的反饋控制系統(tǒng)能夠有效地抑制電阻壁模, 并指出流體效應(yīng)下等離子體旋轉(zhuǎn)對電阻壁模穩(wěn)定的有效性.Xia 等[6]針對JET-like 的平衡位形研究了等離子體旋轉(zhuǎn)效應(yīng)和反饋控制的協(xié)同作用, 結(jié)果表明等離子體旋轉(zhuǎn)與反饋控制的協(xié)同作用下能促使電阻壁模產(chǎn)生兩個(gè)穩(wěn)定窗, 并且在反饋控制下, 等離子體電阻對電阻壁模有很大影響.Xia 等[7]還研究了在反饋控制下動理學(xué)效應(yīng)對電阻壁模的影響.Liu 等[8]研究了ITER 裝置中等離子體剪切流對電阻壁模的影響.Hao 等[9?11]研究了捕獲熱粒子對電阻壁模的影響, 捕獲能量粒子穩(wěn)定電阻壁模, 以及由黏滯引起的湍流和等離子體旋轉(zhuǎn)對電阻壁模不穩(wěn)定性的協(xié)同作用.

由于ITER 裝置的諸多物理參數(shù)與已有的其他聚變裝置不同, 如ITER 裝置幾何尺寸更大, 需在高比壓、大自舉電流、長脈沖下運(yùn)行.ITER 裝置目標(biāo)平衡對應(yīng)的歸一化比壓 βN= 2.92, 對應(yīng)的比壓參數(shù) Cβ= 0.44, 本文模擬中使用的平衡是在ITER 設(shè)計(jì)平衡的基礎(chǔ)上略調(diào)高了比壓值, Cβ= 0.7,βN= 3.18.ITER 裝置希望運(yùn)行在更高的比壓參數(shù)下, 以獲得更高的聚變功率、自舉電流份額等.而電阻壁模會隨著 βN的升高, 變得更加不穩(wěn)定, 模式的增長率相對更高, 有利于提高模擬結(jié)果的精度(因?yàn)槟繕?biāo)平衡在使用磁通-電壓控制模式且反饋增益為 | G| = 0 時(shí), 模式的增長率已經(jīng)進(jìn)入準(zhǔn)穩(wěn)定狀態(tài), 可見文獻(xiàn)[12]的圖3).對于ITER 這樣的超大型托卡馬克裝置, 放電破裂的破壞性更大, 對裝置中面向等離子體的材料將會造成毀滅性的傷害.因此, 在裝置運(yùn)行中必須有效控制電阻壁模不穩(wěn)定性的增長.

對電阻壁模的控制一般可以分為被動控制和主動控制兩種手段.被動控制是利用模式與波發(fā)生共振阻尼[13,14], 把不穩(wěn)定模式的自由能耗散掉.主動控制是通過在真空室內(nèi)或外部安裝的反饋線圈補(bǔ)償泄露的磁場[15], 從而控制電阻壁模.近期研究發(fā)現(xiàn)使用主動控制和被動控制的協(xié)同作用能更好地控制電阻壁模[6].

本文利用MARS-F 程序[16]對ITER 裝置電阻壁模不穩(wěn)定性進(jìn)行了模擬, 分別研究了流體模型下等離子體旋轉(zhuǎn)、反饋控制及協(xié)同作用對電阻壁模不穩(wěn)定性增長率的影響.文章安排如下: 第二部分將簡要介紹使用的MARS-F 程序的模型, 第三部分將給出使用的ITER 平衡, 第四部分將對數(shù)值計(jì)算結(jié)果進(jìn)行分析和討論, 最后進(jìn)行總結(jié).

2 計(jì)算模型

使用線性模型研究電阻壁模不穩(wěn)定性及其控制是目前所有模擬中公認(rèn)的方法, 使用線性模型是因?yàn)殡娮璞谀５脑鲩L率尺度較小, 它的非線性項(xiàng)貢獻(xiàn)可以忽略不計(jì).MARS[17]程序是一個(gè)線性代碼,在環(huán)幾何位形下自洽求解電阻磁流體方程組, 程序不僅考慮了環(huán)向等離子體旋轉(zhuǎn), 而且把電阻導(dǎo)體壁、外加反饋線圈以及各種阻尼效應(yīng)也引入到模型中.MARS 程序聯(lián)立等離子體區(qū)域的非理想磁流體線性化方程組、真空區(qū)域方程、薄壁近似以及外加反饋線圈方程求解得到不穩(wěn)定模式的本征值.下面簡單地介紹一下本文使用的MARS 程序模型.

等離子體的方程為[17,18]:

這里 γ 是復(fù)數(shù), 代表電阻壁模的増長率和實(shí)頻, 由多普勒位移 i n? 修正, n 是環(huán)向模數(shù), ? 是沿著環(huán)向 ? 的等離子體旋轉(zhuǎn)頻率.B, J 和P 分別為由平衡程序CHEASE[16]求解得到的平衡磁場、平衡電流密度和平衡壓強(qiáng).v, b, j 和p 分別表示擾動速度、擾動磁場、擾動電流密度和擾動壓強(qiáng).ρ 是擾動質(zhì)量密度, R 是等離子體大半徑, Z? 是在垂直方向的單位矢量, Π 是黏性應(yīng)力張量, 表示平行聲波黏滯阻尼[19],代表阻尼強(qiáng)度, k 表示聲波數(shù) ( n ?m/q)(1/R) ,表示離子熱速度.η 是等離子體電阻率, Γ 是比熱比系數(shù).

在真空區(qū)域中, 沒有擾動速度和擾動壓強(qiáng), 且擾動磁場滿足:

導(dǎo)體電阻壁滿足薄壁近似:

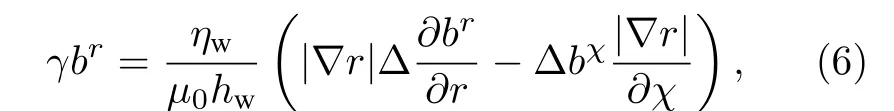
其中 ηW和 hW分別表示導(dǎo)體壁的電阻率和厚度, br,bx分別代表是擾動磁場逆變量的分量, 在托卡馬克曲線坐標(biāo) ( r,χ,?) 中, 有

其中r 是徑向坐標(biāo), 定義為極向磁通的平方根, χ是極向坐標(biāo), 依賴于雅可比行列式的選擇.

反饋線圈方程為[12]

其中 ψf, If, Rf和 τf分別表示穿過反饋線圈的擾動磁通、線圈電流、電阻以及反饋線圈的響應(yīng)時(shí)間,G 表示反饋系統(tǒng)增益, 反饋增益是工程參數(shù), 在控制過程中通過調(diào)整反饋控制系統(tǒng)的PID 參數(shù)來實(shí)現(xiàn)對系統(tǒng)的有效控制.本文中的G 相當(dāng)于PID 系統(tǒng)的比例項(xiàng)系數(shù).這里G 是歸一化的參數(shù), 歸一化因子為無量綱量 Kp和 Kd表示反饋控制器中的比例和微分因子, bs為傳感器線圈內(nèi)測量/響應(yīng)的噪聲, 這里也是用磁場表示的.

3 平衡與比壓

采用ITER 裝置等離子體電流 IP= 9 MA 的先進(jìn)運(yùn)行平衡位形, 其能量增益Q = 5, 輸出功率P = 340 MW, 真空環(huán)向磁軸處磁場 B0= 5.3 T,等離子體大半徑 R0= 6.2 m, 小半徑 a = 2.0 m.ITER 裝置的極向截面如圖1 所示, 真空室分為內(nèi)外兩層, 在內(nèi)層真空室弱場側(cè)偏上、中間、偏下分別安裝了三組磁擾動線圈, 用于控制邊緣局域模和電阻壁模不穩(wěn)定性, 以及內(nèi)側(cè)中心平面處的一組傳感器, 用來測量極向磁擾動.

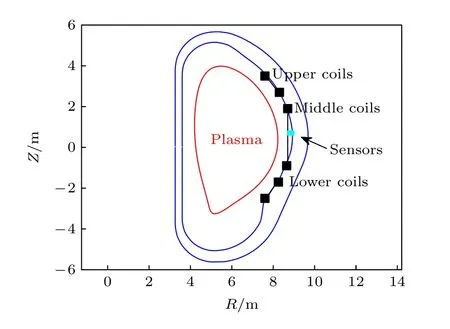
圖1 ITER 裝置極向截面及反饋控制示意圖Fig.1.Geometry of poloidal cross section and feedback control in ITER.

圖2 給出了ITER 裝置9 MA 先進(jìn)運(yùn)行平衡的各平衡量剖面分布, 圖2(a)是安全因子, 在芯部有較弱的負(fù)磁剪切, 磁軸處的安全因子為 q0=2.44, 邊界處的安全因子達(dá)到 qa= 7.13, 安全因子最小值為 qmin= 1.60, 這種弱剪切的結(jié)構(gòu)能產(chǎn)生較高的比壓, 是托卡馬克先進(jìn)運(yùn)行方案的一個(gè)重要特點(diǎn).圖2(b)是等離子體壓強(qiáng)分布, 壓強(qiáng)使用磁壓歸一化, 圖2(c)是等離子體質(zhì)量密度剖面, 圖2(d)是等離子體環(huán)向電流密度剖面, 使用B0/(μ0R0)進(jìn)行了歸一化處理.

圖2 ITER 裝置9 MA 先進(jìn)運(yùn)行平衡 (a)安全因子剖面; (b)等離子體壓強(qiáng)剖面, 由 B 02/μ0 歸一化; (c)質(zhì)量密度剖面, 磁軸處歸一化為1; (d)環(huán)向電流密度剖面, 由 B 0/(μ0R0) 歸一化, s = , ψ 是歸一化的極向通量Fig.2.Radial profiles of (a)safety factor; (b)equilibrium pressure normalized by factor B 02/μ0 ; (c)plasma density normalized to unity at the magnetic axis; (d)toroidal current density normalized by factor B 0/(μ0R0) and s = ψ is the normalized poloidal flux for ITER target plasma designed for 9 MA steady state scenario.

針對圖2 給出的平衡位形, 固定電阻壁的位置在 d /a=1.29 和環(huán)向模數(shù) n =1 , 運(yùn)用MARS 程序計(jì)算得到了有理想壁和無壁的時(shí)候外扭曲模的增長率和比壓的關(guān)系, 如圖3 所示.所得到的計(jì)算結(jié)果表明, 在無壁時(shí), 比壓極限為; 在有理想壁存在時(shí), 比壓極限為=3.48 (其中βN=β(%)a(m)B0(T)/Ip(MA) 是 歸 一 化 比 壓, β 是等離子體熱壓與磁壓的比值, a 是等離子體小半徑,B0是環(huán)向等離子體磁軸處的磁場, Ip是等離子體總電流).這里定義一個(gè)等離子體比壓參量表示無壁時(shí)比壓極限, Cβ=1 表示有理想壁時(shí)比壓極限, 我們在研究電阻壁模的時(shí)候, Cβ會在0 和1 之間取值.

圖3 在無壁和有理想壁時(shí), 不同比壓下的外扭曲模增長率Fig.3.Growth rate of external kink versus β N with and without an ideal wall.

4 數(shù)值結(jié)果與討論

4.1 流體效應(yīng)對電阻壁模的穩(wěn)定作用

對于上面給出的ITER 平衡, 取等離子體比壓參量為 Cβ=0.7 , 研究等離子體旋轉(zhuǎn)頻率對電阻壁模的影響.對于平行黏滯 κ//分別取0.5, 1 和1.5,用MARS 程序計(jì)算得到了不同等離子體旋轉(zhuǎn)頻率下電阻壁模的增長率, 如圖4 所示, 其中等離子體旋轉(zhuǎn)頻率使用阿爾芬頻率 ?A=υA/R0歸一化的.所得到的計(jì)算結(jié)果表明, 在平行黏滯 κ//不變時(shí), 電阻壁模增長率會隨著等離子體環(huán)向旋轉(zhuǎn)頻率增大而減小, 當(dāng)旋轉(zhuǎn)頻率達(dá)到臨界頻率時(shí), 電阻壁模的增長率為零.這是因?yàn)槟Ｊ?波)與離子聲波在有理面附近發(fā)生共振阻尼, 耗散掉驅(qū)動不穩(wěn)定模式的自由能, 從而達(dá)到穩(wěn)定.所得到的計(jì)算結(jié)果還表明,平行黏滯越大, 穩(wěn)定電阻壁模所需的旋轉(zhuǎn)頻率越小, 穩(wěn)定效果越好.這是因?yàn)轲酱? 對壓強(qiáng)驅(qū)動的不穩(wěn)定模式的自由能耗散越大, 模式的增長率越小.

圖4 等離子體比壓參量為 C β =0.7 、平行黏滯 κ // 分別取0.5, 1 和1.5 時(shí), 不同等離子體旋轉(zhuǎn)頻率下的電阻壁模增長率Fig.4.Growth rate of resistive wall mode versus plasma flow with equilibrium pressure scaling factor C β =0.7 ,parallel viscous coefficient κ // = 0.5, 1, 1.5.

當(dāng)?shù)入x子體比壓參量 Cβ在0.1—0.9 之間變化,等離子體旋轉(zhuǎn)頻率在0— 1.2×10?2范圍內(nèi)變化,用MARS 程序計(jì)算得到了電阻壁模的增長率, 計(jì)算中設(shè)置平行黏滯 κ//=1.5.計(jì)算結(jié)果如圖5 所示.在 Cβ比較小且等離子體具有較高旋轉(zhuǎn)頻率的情況下, 可以得到電阻壁模的穩(wěn)定區(qū)間.隨著 Cβ的增加, 電阻壁模表現(xiàn)得越不穩(wěn)定, 為了擴(kuò)大穩(wěn)定電阻壁模的穩(wěn)定窗口, 在等離子體流體模型下, 僅利用等離子體旋轉(zhuǎn)實(shí)現(xiàn)ITER 裝置電阻壁模的控制是比較困難的, 需要反饋控制的加入.

4.2 反饋控制對電阻壁模的穩(wěn)定作用

用等離子體旋轉(zhuǎn)結(jié)合平行黏滯來穩(wěn)定電阻壁模需要很大的臨界等離子體旋轉(zhuǎn)閾值, 像ITER 等這種大型托卡馬克難以達(dá)到, 需要主動控制(反饋控制)參與.如圖1 所示, ITER 裝置的反饋系統(tǒng)是由三組反饋線圈和一組傳感器組成的, Li 等[20]分析了電壓-電流、電壓-電壓、磁通-電流以及磁通-電壓四種反饋方式, 本工作采用的反饋控制是磁通-電流反饋控制.

圖5 平行黏滯 κ // 取1.5 時(shí), 不同等離子體比壓參數(shù)和不同等離子體旋轉(zhuǎn)頻率下的電阻壁模增長率Fig.5.With parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode versus plasma flow for different equilibrium pressure scaling factor C β.

首先給出主動反饋線圈產(chǎn)生的磁場分布, 如圖6 所示, 以 Cβ= 0.7 為例, 可以看出不加等離子體旋轉(zhuǎn), 只考慮主動反饋線圈時(shí), 在等離子體邊界有比較大的磁場分布, 芯部基本沒有線圈產(chǎn)生的磁場.

圖6 沒有等離子體旋轉(zhuǎn)頻率, C β =0.7 時(shí), 計(jì)算得到的主動線圈產(chǎn)生的磁場分布Fig.6.Without plasma flow and equilibrium pressure scaling factor C β =0.7 , the calculated magnetic field distribution of active coil.

然后, 在研究三組線圈增益前, 為達(dá)到上下兩組線圈相位的最佳組合, 利用MARS-F 程序?qū)ι舷聝山M線圈的相位進(jìn)行了掃描.首先固定上下兩組線圈增益為 | G| = 0.5, 固定一組線圈相位, 去掃描另一組線圈相位, 以找到最佳的相位組合, 如圖7所示, 電阻壁模的增長率隨上下兩組線圈的相位組合不同而不同, 在上下兩組線圈的相位為 ?u=150°, ?L= –150°時(shí), 反饋控制電阻壁模的效果最好, 把這一相位組合稱為最佳相位組合, 和Wang等[12]采用磁通-電壓的反饋控制方式相位掃描的結(jié)果一致, 以下所有上下線圈的研究中, 上下線圈的相位均取 ?u= 150°, ?L= –150.

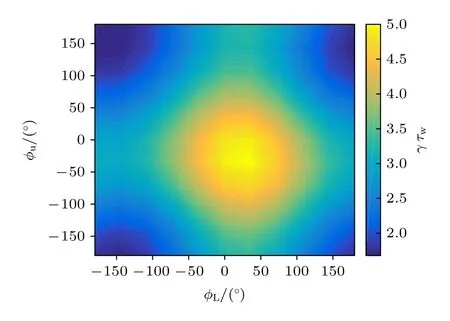
圖7 線圈增益幅值為 | G| = 0.5 時(shí), 上下兩組線圈不同相位下電阻壁模的增長率Fig.7.Growth rate of resistive wall mode with varying phase of feedback gains for upper and lower sets of active coils, feedback gain amplitude | G| = 0.5.

接著, 在沒有等離子體旋轉(zhuǎn)頻率, 平行黏滯κ∥=1.5時(shí), 分別研究了中間反饋線圈、上下兩組反饋線圈及三組反饋線圈的增益對電阻壁模的影響, 如圖8—圖10 所示.對比發(fā)現(xiàn), 等離子體比壓越大, 所需要穩(wěn)定電阻壁模的臨界增益越大; 在不同等離子體比壓下, 當(dāng)反饋增益逐漸增大時(shí), 增長率慢慢變小, 當(dāng)增益幅值足夠大時(shí), 能使得電阻壁模的增長率為零, 穩(wěn)定電阻壁模, 這是因?yàn)橥ㄟ^導(dǎo)體壁泄露的磁場已由中間反饋線圈得到補(bǔ)償, 此時(shí)導(dǎo)體壁等效為理想壁.定義完全穩(wěn)定電阻壁模的增益為臨界反饋增益 Gcri, 當(dāng)G > Gcri時(shí), 電阻壁模是穩(wěn)定的, 當(dāng)G < Gcri時(shí), 電阻壁模仍然會增長,最終影響高比壓等離子體放電.例如在 Cβ= 0.6時(shí), 中間一組線圈穩(wěn)定電阻壁模所需的臨界增益為|G|= 1.2, 上下兩組線圈穩(wěn)定電阻壁模所需的臨界增益為 | G| = 1.6, 上中下三組線圈穩(wěn)定電阻壁模所需的臨界增益為 | G| = 0.7, 可見, 在只有反饋控制中, 上中下三組反饋線圈的控制效果更好.

4.3 電阻壁模的協(xié)同控制

圖8 在沒有等離子體旋轉(zhuǎn)頻率、平行黏滯 κ // =1.5 時(shí),不同的等離子體比壓參量, 不同中間線圈的增益下電阻壁模的增長率變化Fig.8.Without plasma flow and with parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for middle sets of active coils.

圖9 在沒有等離子體旋轉(zhuǎn)頻率、平行黏滯 κ // =1.5 時(shí),不同的等離子體比壓參量, 不同上下兩組線圈的增益下電阻壁模的增長率變化Fig.9.Without plasma flow and with parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for upper and lower sets of active coils.

前面兩節(jié)分別研究了被動控制和主動控制單獨(dú)對電阻壁模的穩(wěn)定作用, 當(dāng)旋轉(zhuǎn)頻率超過一定閾值或反饋增益足夠大時(shí), 電阻壁模能被完全穩(wěn)定住.然而在實(shí)際裝置運(yùn)行中, 兩種控制手段同時(shí)存在, 例如裝置放電時(shí)給等離子體輔助加熱的中性束注入會產(chǎn)生等離子體旋轉(zhuǎn), 控制其他不穩(wěn)定性模式的反饋線圈對電阻壁模也有穩(wěn)定作用等等.所以接下來研究ITER 裝置中等離子體旋轉(zhuǎn)與反饋對電阻壁模的協(xié)同作用.

圖10 在沒有等離子體旋轉(zhuǎn)頻率、平行黏滯 κ // =1.5 時(shí),不同的等離子體比壓參量, 不同上中下三組線圈的增益下電阻壁模的增長率變化Fig.10.Without plasma flow and with parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for all three sets of active coils.

固定等離子體旋轉(zhuǎn)頻率 ?0/?A= 0.002,?0是等離子體中心處的旋轉(zhuǎn)頻率, 平行黏滯 κ//=1.5 ,黏滯提供了離子聲波阻尼穩(wěn)定機(jī)制, 考慮磁通-電流反饋控制, 發(fā)現(xiàn)反饋控制和旋轉(zhuǎn)共同作用比單獨(dú)反饋控制能夠更好地穩(wěn)定電阻壁模.例如 Cβ=0.6 時(shí), 只有反饋控制存在(三組反饋線圈同時(shí)加入), 沒有等離子體旋轉(zhuǎn)頻率時(shí), 完全穩(wěn)定電阻壁模所需要的反饋增益為 | G| = 0.7, 如圖10 所示; 當(dāng)再加入等離子體旋轉(zhuǎn)頻率 ?0/?A= 0.002 時(shí), 完全穩(wěn)定電阻壁模所需要的反饋增益為 | G| = 0.6, 如圖13 所示.可見, 反饋加入旋轉(zhuǎn)可以降低穩(wěn)定電阻壁模的臨界增益, 可以更好地控制電阻壁模.

圖11 在等離子體旋轉(zhuǎn)頻率 ? 0/?A = 0.002、平行黏滯κ// =1.5時(shí), 不同的等離子體比壓參量, 加上旋轉(zhuǎn)后中間線圈的增益和增長率的變化Fig.11.With plasma flow ? 0/?A = 0.002 and parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for middle sets of active coils.

圖12 在等離子體旋轉(zhuǎn)頻率 ? 0/?A = 0.002、平行黏滯κ// =1.5時(shí), 不同的等離子體比壓參量, 加上旋轉(zhuǎn)后上下兩組線圈的增益和增長率的變化Fig.12.With plasma flow ? 0/?A = 0.002 and parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for upper and lower sets of active coils.

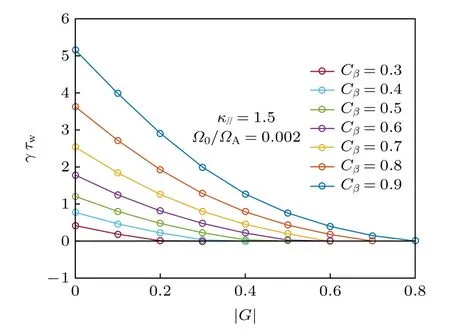
圖13 在等離子體旋轉(zhuǎn)頻率 ? 0/?A = 0.002、平行黏滯κ// =1.5時(shí), 不同的等離子體比壓參量, 加上旋轉(zhuǎn)后上中下三組線圈的增益和增長率的變化Fig.13.With plasma flow ? 0/?A = 0.002 and parallel viscous coefficient κ // =1.5 , growth rate of resistive wall mode with varying equilibrium pressure scaling factor versus feedback gains for all three sets of active coils.

接著分別研究在各個(gè)平衡壓強(qiáng)下, 中間線圈、上下兩組線圈和上中下三組線圈與等離子體旋轉(zhuǎn)的協(xié)同作用, 如圖11—圖13 所示.例如 Cβ= 0.6時(shí), 在中間反饋線圈與等離子體旋轉(zhuǎn)的共同作用下, 穩(wěn)定電阻壁模需要的臨界增益為 | G| = 1.0; 在上下兩組線圈與等離子體旋轉(zhuǎn)的共同作用下, 穩(wěn)定電阻壁模需要的臨界增益為 | G| = 1.4; 在上中下三組線圈與等離子體旋轉(zhuǎn)的共同作用下, 穩(wěn)定電阻壁模需要的臨界增益為 | G| = 0.6.可見, 在三組線圈與等離子體旋轉(zhuǎn)的作用下穩(wěn)定效果最好.

5 結(jié) 論

本文研究了在ITER 裝置上電阻壁模的主動控制和被動控制, 給出了ITER 裝置先進(jìn)運(yùn)行平衡位形; 用MARS 程序在流體模型下研究了等離子體旋轉(zhuǎn)對電阻壁模穩(wěn)定的物理機(jī)理; 使用磁通-電流反饋控制系統(tǒng), 控制系統(tǒng)包括三組反饋控制線圈和一組極向傳感器, 用MARS 程序掃描了上下兩組線圈穩(wěn)定電阻壁模的最佳組合相位; 研究了單獨(dú)反饋控制時(shí), 穩(wěn)定電阻壁模的臨界增益及穩(wěn)定電阻壁模的物理機(jī)理; 研究了在等離子體旋轉(zhuǎn)和反饋控制共同作用下對電阻壁模的控制, 研究表明反饋控制的加入, 不僅可以降低穩(wěn)定電阻壁模的旋轉(zhuǎn)頻率, 而且能夠更快地達(dá)到穩(wěn)定.

本文的研究結(jié)果對中國聚變工程試驗(yàn)堆CFETR 的工程設(shè)計(jì)和運(yùn)行具有一定指導(dǎo)意義.

感謝房玉在MARS 程序運(yùn)行過程中給予的幫助和支持, 感謝劉超博士對本工作的有益討論.