三量子比特Dicke 模型中的兩體和三體糾纏動力學*

毛麗君 張云波

1) (太原師范學院物理系, 晉中 030619)

2) (浙江理工大學理學院, 杭州 310018)

本文利用絕熱近似方法和精確對角化方法研究三量子比特Dicke 模型中的糾纏動力學.處于兩種典型的糾纏態GHZ 態和W 態上的量子比特在時間演化過程中與輻射光場發生強耦合作用, 在各種子系統間產生糾纏,通過分析這些糾纏的演化特性發現初始GHZ 態的三體糾纏魯棒性比W 態強, 這與旋波近似結論一致.與旋波近似下結果不同的是, 兩種態中任意一對量子比特間的糾纏都隨時間演化到幾乎為零, 而三體糾纏隨時間周期演化, 且糾纏程度相對較強, 說明系統中的強耦合作用通過抑制量子比特中的對糾纏來支持三體糾纏.

1 引 言

腔體中原子和電磁場的耦合對光與物質相互作用的理解是至關重要的, 也是許多量子技術的核心.在最近幾年, 人們感興趣的光和物質的相互作用不再是傳統的弱耦合區域[1], 在許多實驗中電子、分子、激子與微腔中光子的相互作用已達到了超強耦合區域[2].此外, 在電路量子電動力學領域中, 通過人造原子實現了光與物質耦合的類似模型, 即超導兩能級系統與微波光子的耦合.在這種情況下, 通過高阻抗諧振器或電流耦合機制超越了原有的界限, 進入到了深強耦合區域[3?6].在強耦合條件下, 相互作用中的非旋波項不能忽略, 人們便開始著手研究非旋波近似下光與物質的耦合系統.

在非旋波近似下, 最簡單的系統是單個二能級系統(稱為量子比特)和光場相互作用的Rabi 模型[7], 人們詳盡地探討了這個模型[8?15], 并將其推廣到多個量子比特和單模量子化光場相互作用的Dicke 模型[16], 發現許多非常有趣的現象[17?22].文獻[23]系統地研究了各向異性量子Rabi 模型的量子相變問題, 在這樣一個有限自由度系統的相變中建立了普適性概念, 還進一步將結論推廣到任意原子數的Dicke 模型中, 并與熱力學極限下的傳統普適性概念等價起來[23].量子糾纏在量子相變中扮演著非常重要的角色, 是量子信息科學的核心.目前, 人們對Dicke 模型中不同子系統間的糾纏演化進行了廣泛的研究[24?30].我們利用絕熱近似方法嚴格求解了三量子比特Dicke 模型的本征解, 并在此基礎上討論了三量子比特和光場的糾纏以及量子比特1 和23 的兩體糾纏隨時間的演化特性[31].除這兩類糾纏以外, 光場和量子比特間的相互作用也會導致其余不同子系統間產生糾纏, 例如, 任意兩個量子比特間的對糾纏、量子比特和光場結合的子系統與其余量子比特的兩體糾纏, 即合作糾纏等等.量子態隨時間演化時, 不同子系統間的糾纏相互競爭, 那么該模型中相互作用到底支持哪一類糾纏, 這個問題有待進一步討論.另外, 三量子比特內部的兩體糾纏是把三體系統分解成1 和23 兩個子系統, 無法區分是1 和2 的糾纏, 還是1 和3 的糾纏, 抑或是1, 2, 3 之間的糾纏[32?35], 即三體糾纏, 決定系統動力學演化的關鍵信息.基于此, 本文將利用糾纏并發度和負值度對這些糾纏動力學特性進行深入研究.

2 三量子比特Dicke 模型的本征解

本文主要討論三個全同的量子比特同輻射場耦合時, 不同子系統之間的糾纏行為, 哈密頓量可以寫為

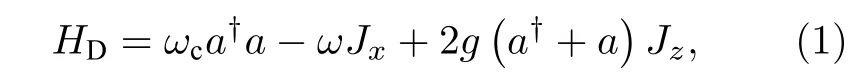
這里, a?(a) 代表頻率為 ωc的單模輻射場的產生(湮滅)算符, ω 為三個量子比特的躍遷頻率, 它們與輻射場的耦合強度都為g, J =Jxex+Jyey+表示三量子比特的總自旋算符, 與哈密頓量對易系統希爾伯特空間可分解為[36]

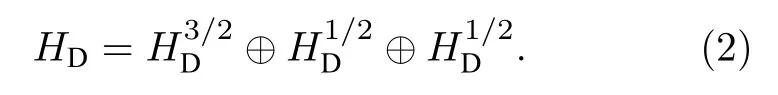
下面簡單介紹一下系統的本征解, 選擇總自旋和光場的結合態 | 3/2,m〉|n〉Am為基矢, | n〉Am代表平移Fock 態, | j,m〉 是 總自旋算符 J2和 Jz的共同本征態.當量子比特的躍遷頻率與單模輻射場頻率滿足關系式 ω ?ωc時, 可以利用絕熱近似方法將哈密頓量簡化為對角塊的形式[31], 即

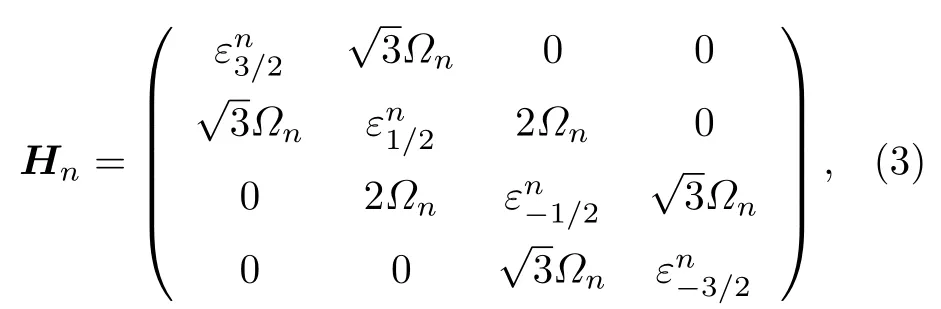
計算可得 Hn中的各個元素為表 示 平 移Fock 態的內積, 將其展開可得

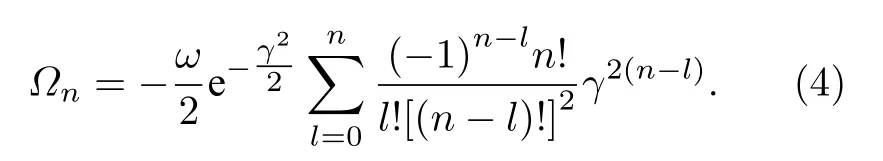
依據宇稱對稱性可得出 Hn的本征能量,

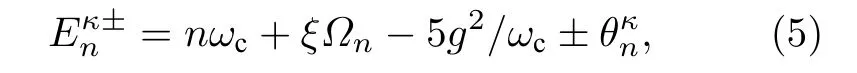
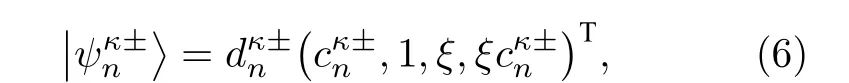
3 糾纏動力學

3.1 GHZ 初態

假設輻射場為相干態 |z〉 , 其中參數z 決定平均光子數(也就是它的模平方), 三量子比特初始處于GHZ 態 ( |111〉+|000〉)/.其中任意一個比特與剩余所有比特之間具有最大的糾纏, 從這個意義上通常認為它是一個最大多方糾纏態.約化掉任意一個量子比特后, 剩余兩量子比特為非糾纏的混合態.在總自旋表象下, 初態可以表示為

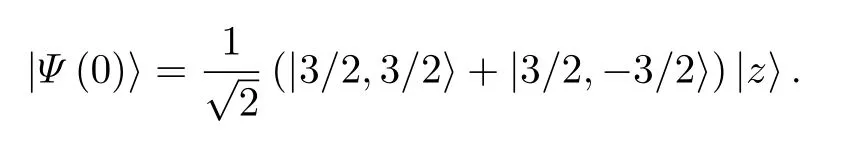
當耦合強度g 相對較小時, 初態可按平移Fock態展開為

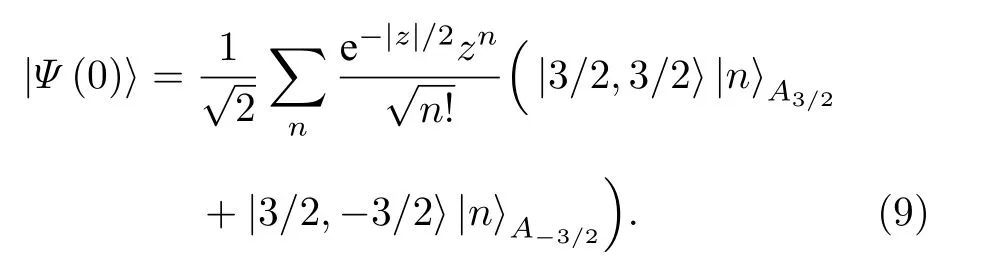
利用薛定諤方程得出系統隨時間演化的密度算符

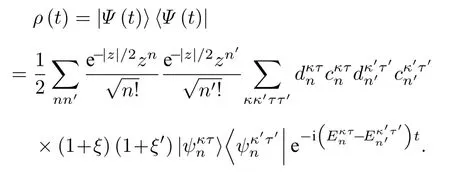
將本征解(7)式和(8)式代入密度算符中, 對光場取跡可得三量子比特約化密度矩陣, 其在Jx表象下的最簡化形式為

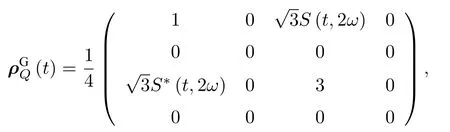
[37], 振蕩函數 Sk(t,ω)=hkexp(ΦRe+iΦIm) , 其特征參數為復原高度包絡因子μk)2fγ2/2 及快速振蕩條件ΦIm=tan?1(πkf)/2+μ(1 ?f)+2πk|z|2, 其中 f =|γz|2,μk=πk(f +2)/γ2.

下面分別研究各類糾纏.對于A 和B 組成的d1×d2維兩體純態系統 | ψAB〉 , 可以利用糾纏兩體純 態I concurrence 的平方I tangle[38]

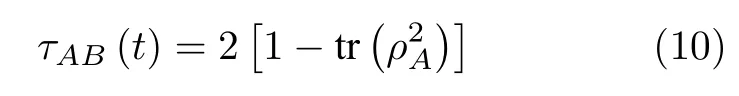
來描述該系統的糾纏程度, 這里的 ρA是子系統A 的約化密度矩陣.依據, 可得 (i) 類糾纏的I tangle[38]

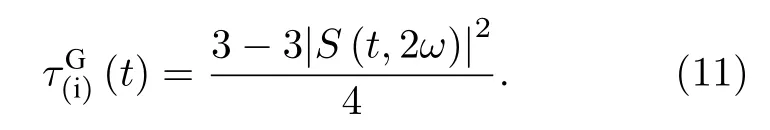
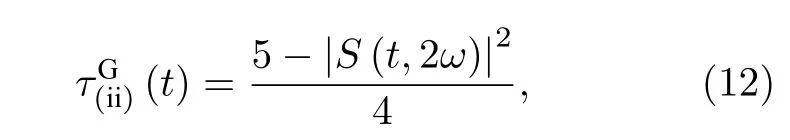
可以用來定量地描述輻射場和量子比特1 結合的子系統與剩余兩量子比特之間的糾纏性質.進一步對密度算符中的量子比特2 取跡, 即

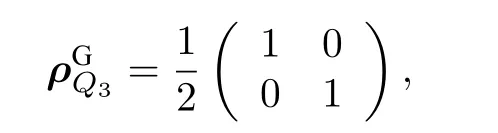
可得 (iii) 類兩體純態I tangle

描述輻射場和量子比特1, 2 結合的子系統與量子比特3 的糾纏特性.另外, 利用密度矩陣可以進一步討論三量子比特間的內部糾纏, 由于混合態密度矩陣的秩是小于等于2 的, 從而可得出描述量子比特1 與2, 3 結合的子系統間的 ( iv) 類混合態I tangle[31,38,39]

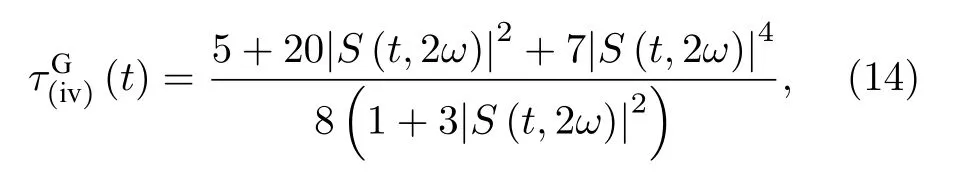
另一方面也可以用糾纏負值度(Negativity)[40]來描述量子比特間的內部糾纏,其中 λi是密度矩陣的部分轉置矩陣的負本征值 , ( iv) 類糾纏負值度為

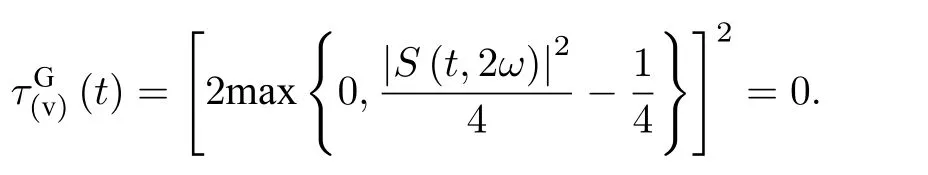
對于矩陣 ρQ23的部分轉置矩陣沒有負本征值, 則兩量子比特糾纏的負值度

在以上分析的基礎上, 可以進一步得到真正的三體糾纏, 即三體糾纏(three-tangle)[33]

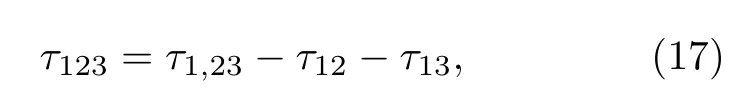
其中 τ1,23描述的是量子比特1 和被認為是單一對象23 的糾纏, τ12, τ13描述 的 分別是1 和2、1 和3 的糾纏.( v) 類I tangle=1, , 每對量子比特之間是經典關聯并不是糾纏, 將其代入(17)式可得, 即某個量子比特與剩余兩個量子比特的糾纏與三體糾纏相等, 這一特性與初始時刻的GHZ 態相同.同樣地, 負性平方也可以用來度量三體糾纏, 定義為 π-tangle[35]

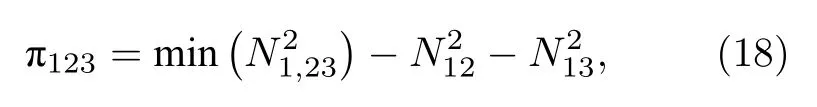
關于π-tangle 的計算涉及到純態糾纏的凸脊擴展,求其最小值幾乎是不可能的.雖然在三量子比特直積態基矢下得到的負性糾纏的平方不一定是最小值, 但一定是三體糾纏的上限值.由(18)式可以得到與并發度相同的結果, 即(t)=

3.2 W 初態

如果假設三量子比特初始時刻處于W 態

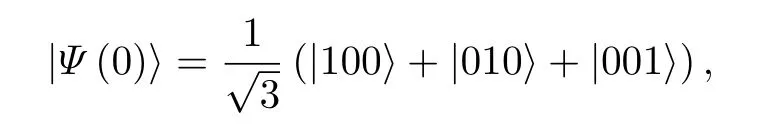
此態對任何一個量子比特取跡后, 剩余的兩量子比特處于糾纏態.用W 態替換GHZ 態重復上面的計算過程, 可得耦合角動量空間中的三量子比特約化密度矩陣

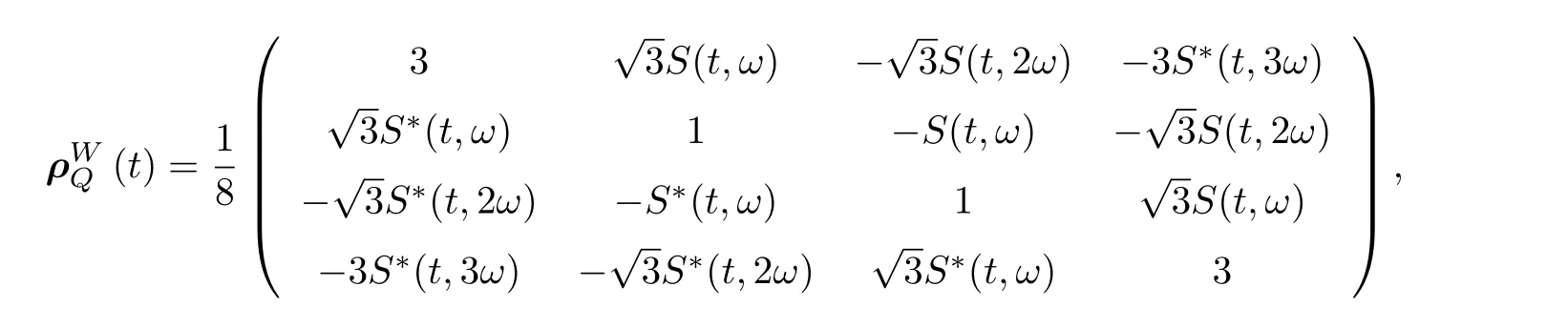
進而利用(10)式得出表征量子比特和光場糾纏的 (i) 類I tangle

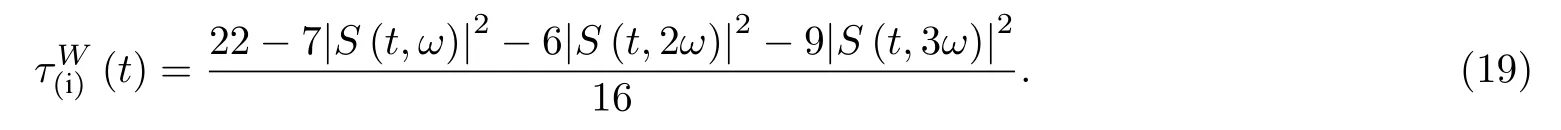
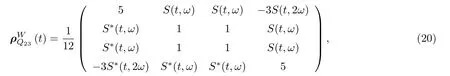
由(20)式可得 ( ii) 類兩體純態I tangle

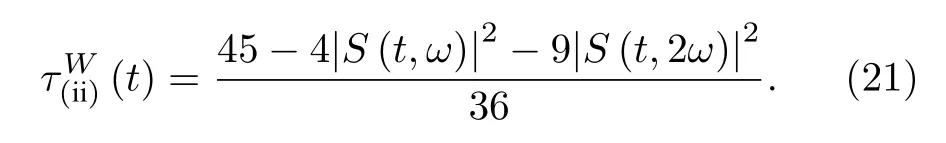
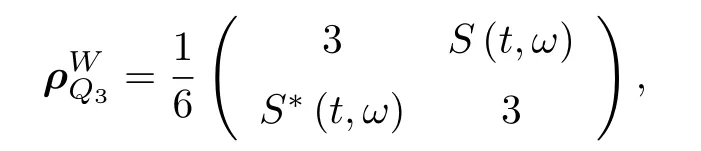
得出 ( iii) 類兩體純態I tangle 的具體表達式

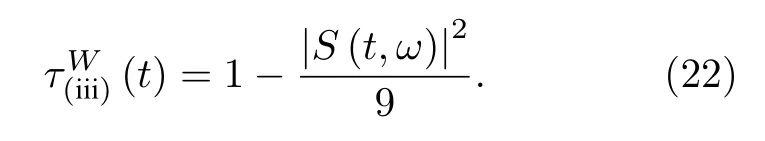
與GHZ 態相比, W 態為初態時系統隨時間演化比較復雜, 約化密度矩陣的秩大于2, I tangle不適用于描述 ( iv) 類混合態糾纏, 但仍然可以通過糾纏負值度來描述該類糾纏特性[31].另外, 依據約化密度矩陣(t) 可得兩量子比特間的糾纏負值度(t) , 進而可以利用(t) 來表征三體糾纏特性.

4 討 論

圖1 初始時刻為GHZ 態(左)和W 態(右)時, (i) 類兩體純態糾纏I tangle, 其中紅色(實線)表示數值結果, 藍色(虛線)表示解析結果, 系統參數為 ω =0.15ωc , z =3 , g =0.02ωc (a) , 0.04ωc (b) , 0.06ωc (c) , 0.08ωc (d)Fig.1.Time evolution of the I tangle for the type (i) with the initial GHZ (left) and W (right) states for ω =0.15ωc , z =3 , and different coupling strengths: g =0.02ωc (a) , 0.04ωc (b) , 0.06ωc (c) , 0.08ωc (d) , given by the numerical method (solid red line),and the analytical approach (dashed blue line).

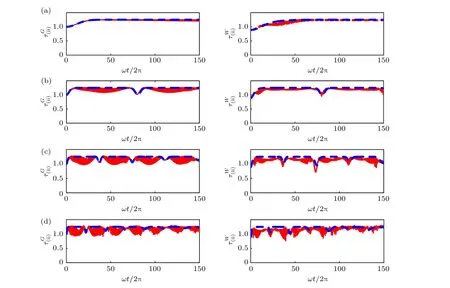
圖2 初始時刻為GHZ 態(左)和W 態(右)時, ( ii) 類兩體純態I tangle 隨時間的演化, 其中紅色(實線)表示數值結果, 藍色(虛線)表示解析結果, 系統參數與圖1 相同Fig.2.Time evolution of the I tangle for the type ( ii) with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line).The corresponding parameters are the same as in Fig.1.

本節將對上一節得到的一些重要結果進行分析與討論.圖1 給出了兩種初態下三個量子比特作為整體與光場的純態糾纏 (i) 類I tangle, 解析結果分別為(11)式和(19)式.圖2 給出了光場和量子比特1 結合的子系統與其余量子比特的純態糾纏(ii)類I tangle, 絕熱近似下的解析解與數值結果的包絡相符合, 左邊表示初態為GHZ 態, 解析結果如(12)式所示, 只包含單一的振蕩因子 S (t,2ω).當初始時刻為W 態時, 解析結果(21)式中包含兩個振蕩因子 S (t,ω) 和 S (t,2ω) , 但通過比較兩個振蕩因子前的系數, 發現仍然是 S (t,2ω) 起決定作用,因此W 態與GHZ 態兩種情形下的 ( ii) 類糾纏演化接近相同, 起初會隨著時間的增加而達到峰值, 穩定一段時間后突然減小而后又有所增加并達到峰值, 且沒有糾纏突然死亡的現象.這個特性與圖1所示的 (i) 類I tangle 是截然不同的, 后者只在W 初態時才能演化到峰值.( ii) 類I tangle 整體上呈周期性振蕩, 且耦合強度越大, 周期越小, 因此可以通過控制兩量子比特與輻射場的耦合強度來調控 ( ii) 類糾纏行為.圖3 給出了GHZ 態和W 態下光場和量子比特1, 2 結合的子系統與量子比特3 糾纏的 ( iii) 類I tangle, 解析結果分別為(13)式和(22)式.當耦合強度較弱時, ( iii) 類I tangle 都接近于1, 無明顯的振蕩因子, 且未發現糾纏死亡現象, 是輻射場與量子比特耦合系統中的糾纏穩態.

圖4 給出了(iv)類糾纏負值度的平方, 即量子比特1 和23 的兩體糾纏, 左圖表示初態為GHZ態時該類糾纏隨時間演化的最小值非零, 沒有發生突然死亡現象, 而右圖中初態為W 態時該類糾纏出現突然消失的現象.圖5 給出了任意一對量子比特的糾纏負值度的平方, 即(v)類糾纏負值度, 左圖中GHZ 態約化后的兩量子比特始于可分離態,而右圖中W 態始于糾纏態, 可以發現兩種初態下隨時間演化的對糾纏都變得很小, 接近于零, 以至于失去了作為信息資源的能力, 這與旋波近似下的結論不同.

在分析了 ( iv) 和 ( v) 兩類糾纏的基礎上, 進一步利用(18)式定義的 π-tangle 討論量子比特之間的三體糾纏.從圖6 可以看出, 隨著耦合強度的增加,解析結果可粗略地描述量子比特間的三體糾纏, 將絕熱近似下的本征解(5)式和(6)式代入約化密度矩陣中, 進而計算 π-tangle, 可以得出更準確的三體糾纏演化規律.無論量子比特處于哪一個初態,在強相互作用下單模輻射場和三量子比特之間會產生糾纏, 即圖1 所示的 (i) 類糾纏, 通過比較圖1 和圖6 發現, 三體糾纏隨時間演化而減弱時, (i)類糾纏就會增強, 反之亦然.圖6 的左側展示了初始時刻為GHZ 態時, 三體糾纏在任何區域都沒有糾纏猝死現象, 并且圖1 左側的 (i) 類糾纏I tangle 沒有演化到最大值.但是W 態情況下(圖6右側), 當三體糾纏隨時間演化突然猝死時, 圖1 右側所示的 (i) 類糾纏I tangle 恰好達到最大值.在不同初態的糾纏演化中, 不發生糾纏猝死的態不容易與外界系統產生糾纏, 且比發生糾纏猝死的態保持糾纏的能力更強, 即魯棒性更強.通過比較兩種初態下的糾纏演化情況, 發現GHZ 態維持三體糾纏的魯棒性比W 態強, 這與旋波近似下的結論一致.但是無論初態是GHZ 態還是W 態, 隨時間演化的對糾纏與三體糾纏相比均很弱, 說明系統中的強耦合通過約束對糾纏以實現對三體糾纏的支持.糾纏態是量子信息領域的基本資源, 其魯棒性會影響糾纏在量子信息中的應用, 該結果可應用于多量子比特信息處理.

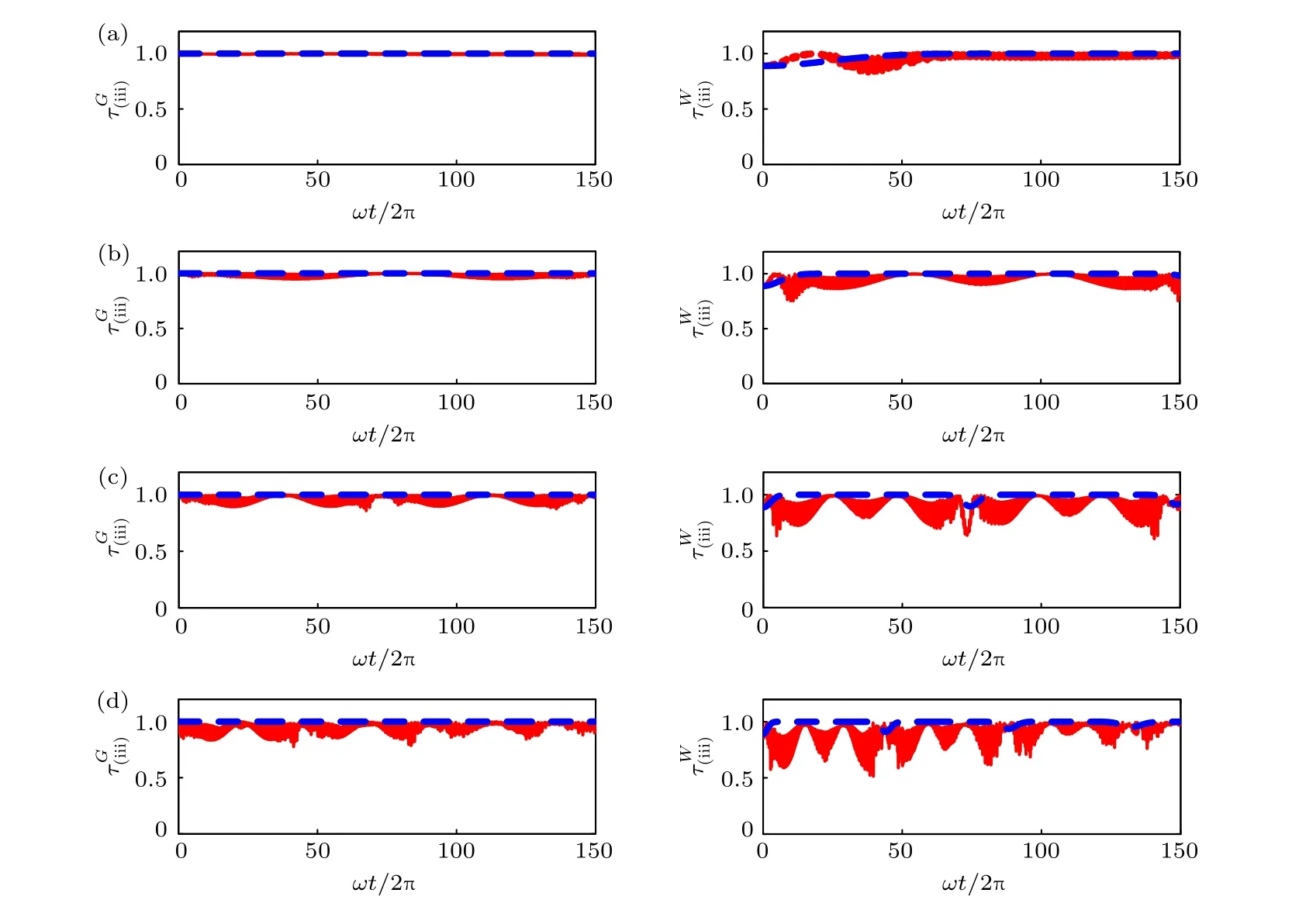
圖3 初始時刻為GHZ 態(左)和W 態(右)時, (iii) 類兩體純態I tangle 隨時間的演化, 其中紅色(實線)表示數值結果, 藍色(虛線)表示解析結果, 系統參數與圖1 相同Fig.3.Time evolution of the I tangle for the type (iii) with the initial GHZ (left) and W (right) states given by the numerical method (solid red line), and the analytical approach (dashed blue line).The corresponding parameters are the same as in Fig.1.

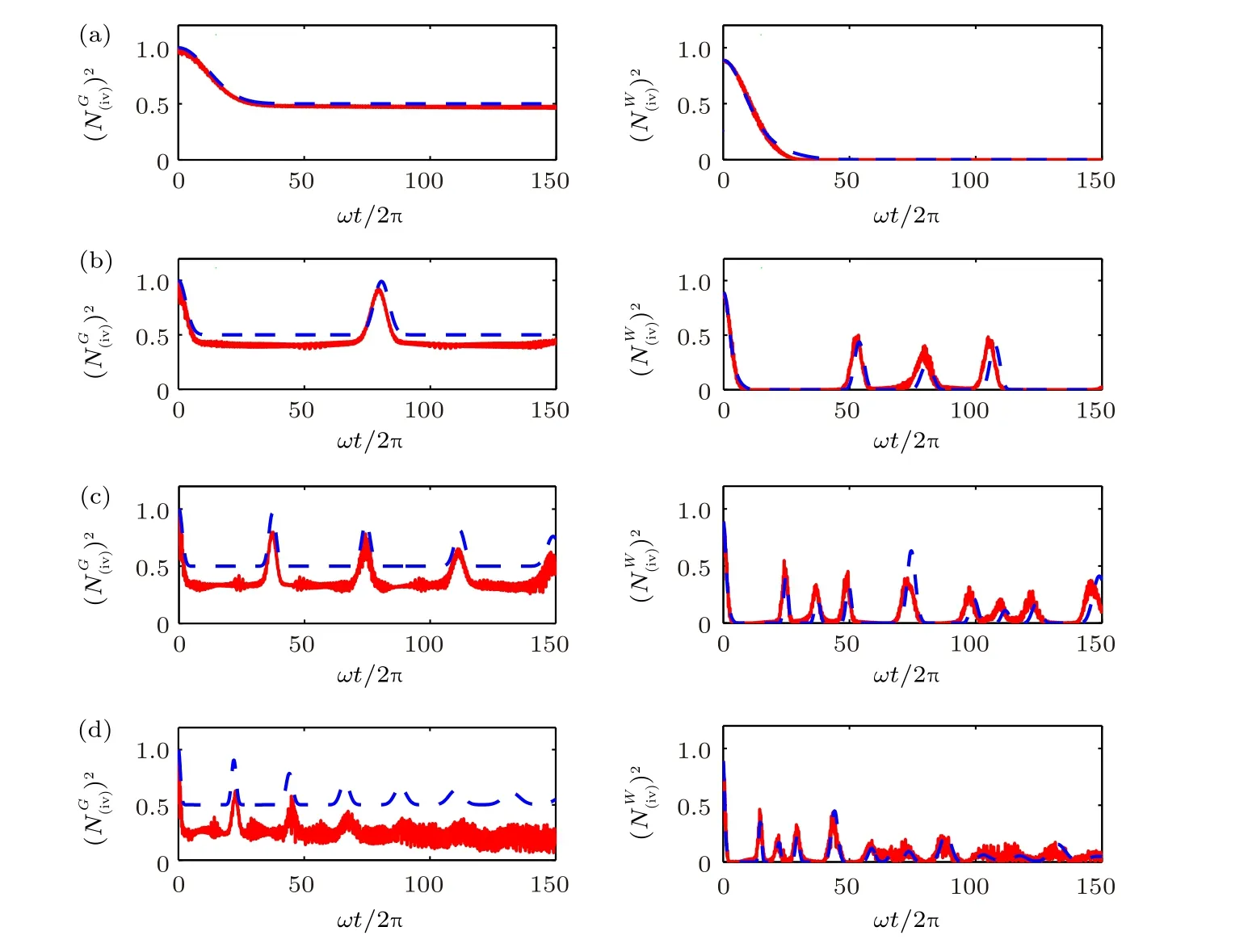
圖4 初始時刻為GHZ(左)態和W(右)態時, (iv)類糾纏負值度的平方隨時間的演化, 其中紅色(實線)表示數值結果, 藍色(虛線)表示解析結果, 系統參數與圖1 相同Fig.4.Time evolution of the square of the negativity for the type (iv) with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line).The corresponding parameters are the same as in Fig.1.

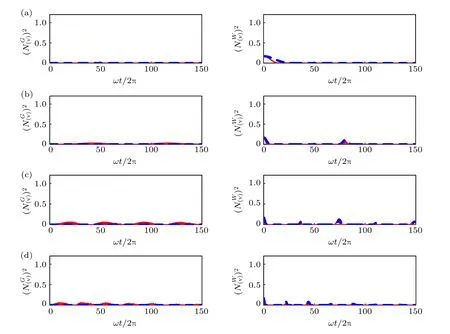
圖5 初始時刻為GHZ(左)態和W(右)態時, (v) 類對糾纏負值度的平方隨時間的演化, 其中紅色(實線)表示數值結果, 藍色(虛線)表示解析結果, 系統參數與圖1 相同Fig.5.Time evolution of the square of the negativity for the type (v) with the initial GHZ (left) and W (right) given by the numerical method (solid red line), and the analytical approach (dashed blue line).The corresponding parameters are the same as in Fig.1.

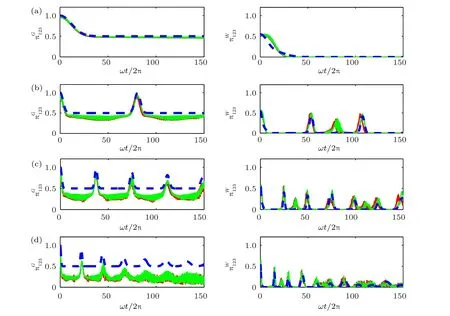
圖6 初始時刻為GHZ(左)態和W(右)態時, 真正的三體糾纏π-tangle 隨時間的演化, 其中紅色(實線)表示數值結果, 綠色(實線)表示絕熱近似結果, 藍色(虛線)表示解析結果, 系統參數與圖1 相同Fig.6.Time evolution of π-tanglewith the initial GHZ (left) and W (right) given by the numerical method (solid red line), the adiabatic approximation method (solid green line) and the analytical approach (dashed blue line).The corresponding parameters are the same as in Fig.1.

5 結 論

利用絕熱近似方法分析了三量子比特Dicke模型全對稱空間中的糾纏演化行為.初始制備在相干態上的輻射場與處于GHZ 態或W 態的三個量子比特發生強耦合作用, 隨著時間的演化不同子系統間產生糾纏, 包括量子比特和場的合作糾纏以及量子比特內的三體糾纏.通過I tangle 和 Negativity來表征糾纏量, 兩者在絕熱近似下的解析表達式能夠很好地展示不同子系統間的糾纏特性.初態為GHZ 態時, 三體糾纏沒有發生糾纏突然死亡的現象, 量子比特和輻射場之間的糾纏隨時間演化時沒有達到最大值, 而W 態恰好相反.表明在相互作用條件下, 三量子比特GHZ 態維持三體糾纏的能力更強, 魯棒性更好, 這與旋波近似下的模型得出的結果相同.與其不同的是, 不論初態是W 態還是GHZ 態, 隨時間演化的任意兩量子比特間的糾纏度都很小, 說明強耦合是通過抑制兩量子比特之間的糾纏來支持三體糾纏的.本文的研究為糾纏態的魯棒性以及利用Dicke 模型實現量子信息處理的工作提供理論參考.