Duffing 系統的主-超諧聯合共振*

李航 申永軍? 楊紹普 彭孟菲 韓彥軍

1) (石家莊鐵道大學, 交通工程結構力學行為與系統安全國家重點實驗室, 石家莊 050043)

2) (石家莊鐵道大學機械工程學院, 石家莊 050043)

非線性動力系統極易發生共振, 在多頻激勵下可能發生聯合共振或組合共振, 目前關于非線性系統的主-超諧聯合共振的研究少見報道.本文以Duffing 系統為對象, 研究系統在主-超諧聯合共振時的周期運動和通往混沌的道路.應用多尺度法得到系統的近似解析解, 并利用數值方法對解析解進行驗證, 結果吻合良好.基于Lyapunov 第一方法得到穩態周期解的穩定性條件, 并分析了非線性剛度對穩態周期解的幅值和穩定性的影響.此外, 由于近似解只能描述周期運動, 不足以描述系統的全局特性, 因而應用Melnikov 方法對系統進行全局分析, 得到系統進入Smale 馬蹄意義下混沌的條件, 依據該條件以及主-超諧聯合共振的條件選取一組參數進行數值仿真.分岔圖和最大Lyapunov 指數顯示出兩個臨界值: 當激勵幅值通過第一個臨界值時, 異宿軌道破裂, 混沌吸引子突然出現, 系統以激變方式進入混沌; 激勵幅值通過第二個臨界值時, 系統在混沌態下再次發生激變, 進入另一種混沌態.利用Melnikov 方法考察了第一個臨界值在多種頻率組合下的變化趨勢, 并用數值仿真驗證了解析結果的正確性.

1 引 言

Duffing 系統是經典的非線性動力系統, 能夠描述轉子系統[1?2]、船舶橫搖[3?4]和受電弓弓頭懸掛系統的垂向振動[5?6]等多種動力學問題, 在微弱信號檢測[7?9]和能量采集[10?11]領域也有應用.目前在對Duffing 振子的研究中, 系統的周期振動解及其穩定性受到學者關注.Shen 等[12,13]研究了分數階Duffing 系統的主共振, 利用平均法得到系統的近似解, 分析了分數階項對系統穩態響應的影響, 提出等效線性剛度和等效線性阻尼的概念.Agarwal 等[14]研究了高斯白噪聲激勵下剛度軟化Duffing 系統的頻響特性, 并通過實驗分析了噪聲幅值對系統跳躍現象的影響, 發現噪聲可以破壞無噪聲系統中的遲滯特性.溫少芳等[15]研究了一類含分數階時滯耦合反饋的Duffing 系統, 利用平均法得到系統的一階近似解, 并分析了反饋系數和分數階項對系統動力學特性的影響, 發現分數階時滯耦合反饋同時具有速度時滯反饋和位移時滯反饋的作用.

通往混沌的道路與混沌控制也是Duffing 系統動力學行為研究的重點問題之一.楊曉麗等[16]研究了有界噪聲與周期激勵下Duffing 系統的混沌運動, 基于Melnikov 方法得到了系統進入混沌運動的必要條件, 討論了噪聲對系統混沌閾值的影響.馬少娟等[17]和吳存利等[18]研究了含隨機參數的Duffing 系統, 利用多項式逼近方法將隨機系統等效為確定性系統, 用確定性系統的方法研究了隨機系統的混沌運動.Niu 等[19]研究了一類分數階Duffing 系統的混沌運動, 利用諧波平衡法得到了原系統的等效整數階系統, 基于Melnikov 方法得到系統進入混沌的條件.在對Duffing 系統周期振動解和混沌運動的研究中也發展了一些新的研究方法.Liu 等[20]提出推廣的廣義胞映射法可用于分數階Duffing 系統的全局分析.Shen 等[21]和Niu等[22]對增量諧波平衡法的推廣可用于分數階系統和強非線性系統的高階近似分析.

非線性系統極易發生共振, 除主共振外還具有一些特殊的共振現象, 如超諧共振[23]、亞諧共振[24]等, 受多頻激勵的非線性系統還可能發生組合共振[25]或者聯合共振[26,27].尤其在聯合共振下,Duffing 系統的穩態周期解可多達7 個分支, 其中包括4 個穩定分支, 系統的響應在穩定分支間的跳躍現象更為復雜.此外, 在多個激勵頻率不可公約時, Duffing 系統將產生概周期響應[28], 并且隨著系統參數改變, 概周期響應容易失穩進入混沌[29].畢勤勝等[30]研究了一類受兩個簡諧激勵且頻率不可公約的Duffing 系統, 對系統在非共振情況下通往混沌的道路進行研究, 發現隨著激勵幅值改變,概周期響應的某一周期分量或某一組合頻率成分將發生倍化分岔導致混沌.在實際問題中, 動力系統往往受到多個激勵源的作用, 因此對多頻激勵的非線性系統進行研究是有必要的.鑒于針對非線性系統在主-超諧聯合共振情況下的研究極為少見,本文以多頻激勵Duffing 系統為對象, 考察系統在主-超諧聯合共振時的周期運動與混沌運動.通過多尺度法得到系統的近似解析解, 研究周期運動在Lyapunov 意義下的穩定性.基于Melnikov 方法分析系統的全局動力學特性, 研究Duffing 系統在主-超諧聯合共振時通往混沌的道路.

2 Duffing 系統的主-超諧聯合共振的一次近似解

研究受兩個簡諧激勵的Duffing 系統:

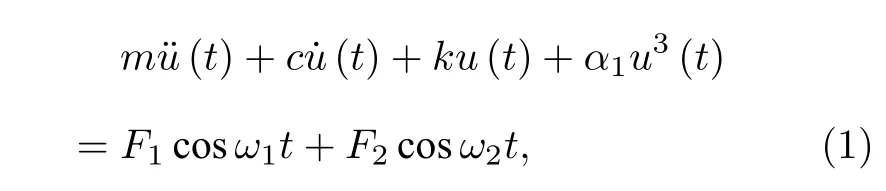
其中 m , c , k , α1, Fi和 ωi( i =1,2 )分 別為系統的質量、線性阻尼系數、線性剛度系數、非線性剛度系數、激勵幅值和激勵頻率.

對系統進行如下坐標變換:

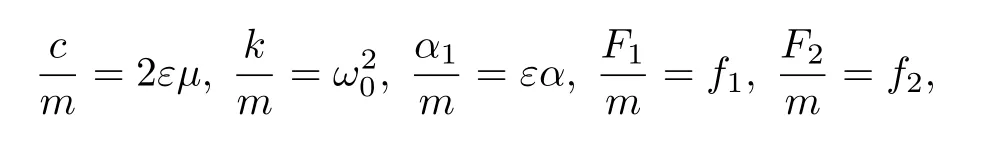
其中 ε 為小參數, 滿足 0 <ε ?1 , ω0為系統的固有頻率.

于是(1)式可以等價地寫成

為研究系統的主-超諧聯合共振, 要求 ω1≈ω0,且 f1為小量, 即

其中 σ1和 σ2為引入的調諧因子, 從而(2)式成為

應用多尺度法[27]研究系統的一次近似解.引入兩個時間尺度 T0=t , T1=εt , 并假設(3)式的解具有如下形式:

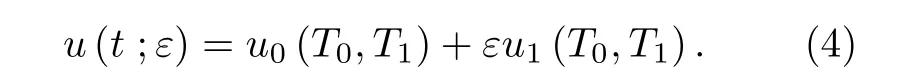
將(4)式代入(3)式, 比較 ε 的同次冪, 得到一組偏微分方程:

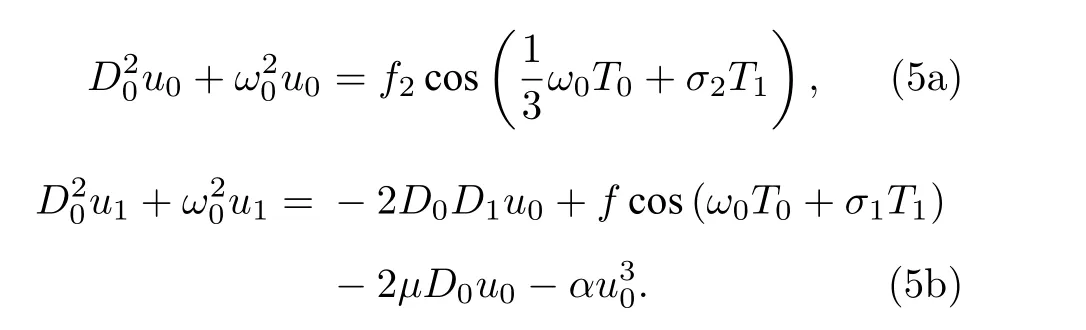
(5a)式的解為

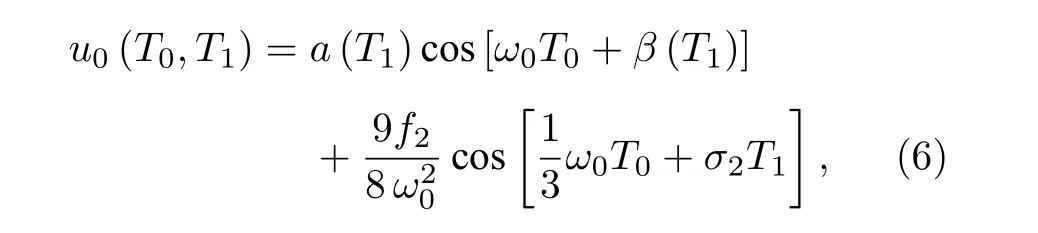
其中 a (T1) 和 β (T1) 分別為慢變振幅和相位.

(6)式可寫成復數形式:

將(7)式代入(5b)式得到:

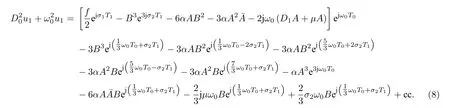
由此得到消除永年項的條件為

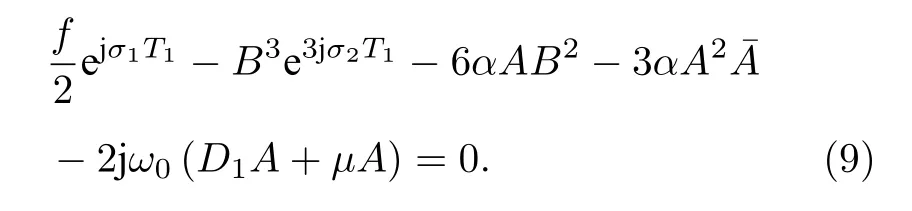
從而系統(1)在主-超諧聯合共振下的一次近似解可以表示為

其中a 和 β 是 T1的函數, 由(10)式確定.

3 周期運動的穩定性

3.1 Lyapunov 意義下的穩定性條件

相比瞬態響應, 穩態響應的穩定性更值得關注.觀察(10)式可以發現, 定常解存在, 即D1a=0和 D1β =0 有解的必要條件是 β ?σ1T1和β ?3σ2T1是常數, 這時有 D1β =σ1=3σ2.進一步可以得到ω1=3ω2, 即只有當兩個激勵頻率滿足此倍數關系時, 才能通過解析方法求得主-超諧聯合共振的定常解.

引入調諧因子 σ =σ1=3σ2, 再令 β ?σT1=φ ,(10)式可以寫成自治的形式:

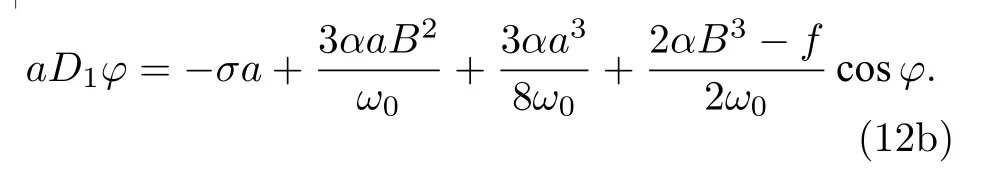
相應的一次近似解變成:

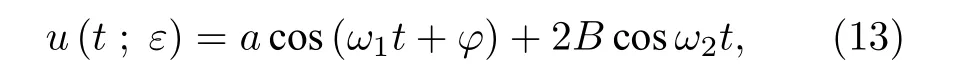
其中 a 和 φ 是 T1的函數, 由(12)式確定.

為檢驗一次近似解(13)式的正確性, 利用變步長四階五級Runge-Kutta 法對系統(1)進行數值仿真并和一次近似解對比, 取系統參數m=1, c=0.02, k =4, α1=0.4, F1=0.1, F2=2,ω2=ω1/3.首先對比穩態響應的幅頻曲線, 仿真時長 t =1000 , 取后 2 0% 響應的最大值為穩態幅值,得到解析解與數值解的幅頻曲線對比結果如圖1所示.然后對比位移時間歷程, 取激勵頻率 ω1=2.2 ,ω2=ω1/3 , 解析解初值取 ( a0,φ0)=(0.1,0) , 對應的數值解初值由(13)式計算, 仿真得到解析解與數值解的位移時間歷程對比結果如圖2 所示.

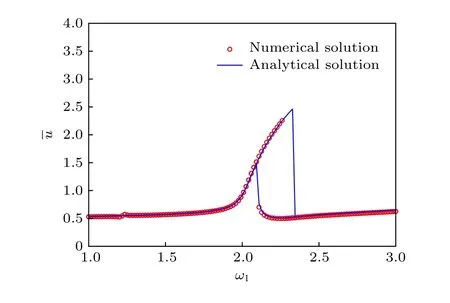
圖1 幅頻曲線對比Fig.1.Comparisons of amplitude-frequency curves.

從圖1 和圖2 中可見, 解析解和數值解在較寬的頻率范圍內吻合良好, 即使是瞬態響應也能夠較為精確地描述.此外, 從圖1 中可以看到系統的穩態響應在一定頻率范圍內具有多值性, 事實上, 系統的多值性和穩定性都由近似解中的第一部分, 即a cos(ω1t+φ)支配.因此, 在系統周期運動的穩定性分析中只需考察這一部分.

圖2 位移時間歷程對比 (a) 瞬態響應; (b) 穩態響應Fig.2.Comparisons of displacement time histories: (a) Transient response; (b) steady-state response.

令(12)式中的 D1a=0 , D1φ=0 , 可以得到

定常解的振幅 aˉ 和相位 φˉ 滿足的方程組:

從(14)式導出定常解的幅頻響應方程和相頻響應方程分別為

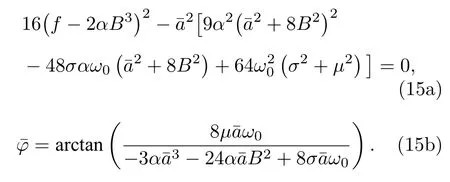
下面考察定常解的穩定性, 定義狀態向量V =[a,φ]T, 構造向量函數:

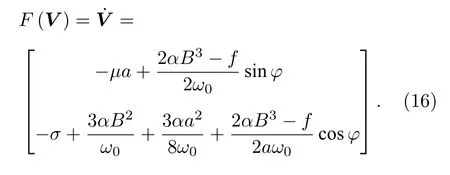
其中 P =trJ , Q =det[J].

根據Lyapunov 第一方法[31], 系統在定常解處 漸近穩定的條件是 P <0 且 Q >0.對于阻尼系統, 總有 P <0 , 因此系統的穩態周期運動在Lyapunov 意義下的穩定性條件為

3.2 數值仿真

仍取參數 m =1 , c =0.02 , k =4 , F1=0.1 ,F2=2 , ω2=ω1/3.由(15)式計算定常解的幅頻特性和相頻特性, 再由(18)式判斷對應解支的穩定性, 得到 α1=0.4 和 α1=?0.4 時定常解的幅頻曲線和相頻曲線分別如圖3 和圖4 所示.從圖3 和圖4 可見, 系統最多存在2 個穩定解支和1 個不穩定解支, 且圖3(b)的多值區域與圖1 吻合.如前所述, 許多工程振動問題都可以由Duffing 系統描述.轉子系統在啟停過程中可能經過共振區, 這時系統的響應將會在多個穩定解支之間切換, 振幅突然增大或減小, 稱為跳躍現象.Wang 等[11]基于Duffing系統設計了一種能量采集裝置, 在能量采集實驗中觀察到這種跳躍現象.

確定穩態響應的多值和不穩定的頻率范圍是一個重要問題, 利用解析解能夠在短時間內計算得到較為精確的結果.利用(15)式和(18)式仿真得到非線性剛度系數 α1對系統的影響如圖5 所示.對于剛度軟化系統, 隨著系統剛度逐漸軟化, 共振峰逐漸降低, 多解區域擴大; 對于剛度硬化系統,隨著系統逐漸硬化, 共振峰也逐漸降低, 但對多解區域影響不大.

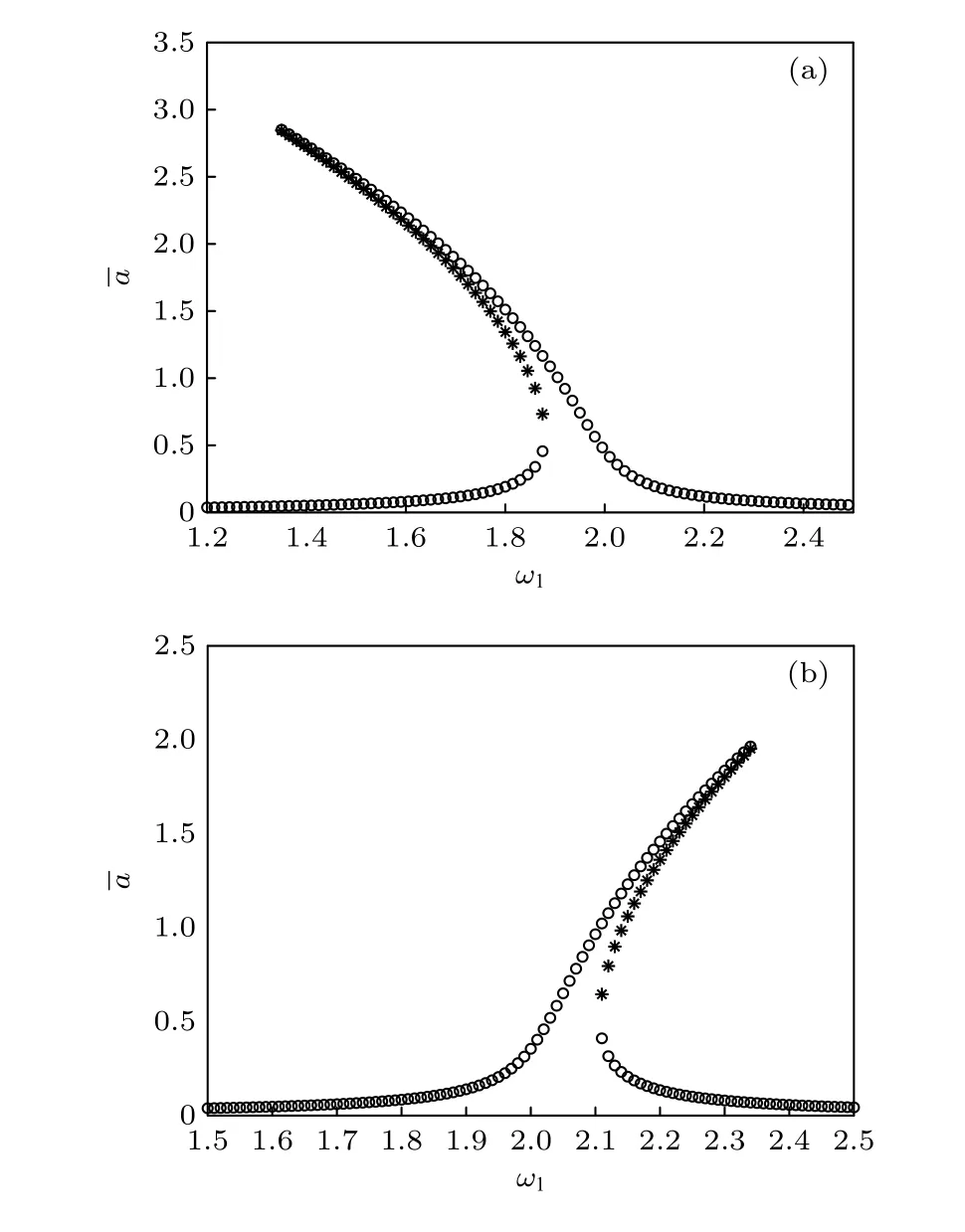
圖3 定常解的幅頻曲線 (a) α 1=?0.4 , 剛度軟化; (b)α1=0.4, 剛度硬化 (圓表示穩定解支, 星號表示不穩定解支)Fig.3.Amplitude-frequency curves of steady-state response:(a) α 1 =?0.4 , stiffness softening; (b) α 1 =0.4 , stiffness hardening (the circles for stable solution and the asterisks for unstable one).

4 混沌運動分析

4.1 系統的混沌閾值

攝動理論得到的近似解具有一定局限性.由于系統在一定條件下可能進入混沌, 此時近似解無法描述系統的響應, 因而需對系統進行全局分析, 確定系統的混沌閾值.Melnikov 方法是檢測動力系統混沌閾值的常用解析方法, 通過考察過鞍點的穩定流形和不穩定流形之間的距離, 得到系統的同宿軌道或異宿軌道發生橫截相交的數學條件, 從而可以判斷系統是否進入Smale 馬蹄意義下的混沌.

在此考慮系統(1)剛度軟化(即 α1<0 )的情況, 對(1)式進行如下坐標變換

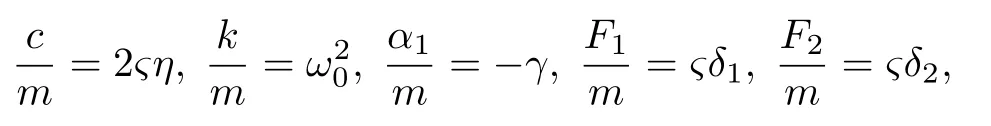
其中 ? 為小參數.從而(1)式可以寫成:

將(19)式寫成狀態方程形式:

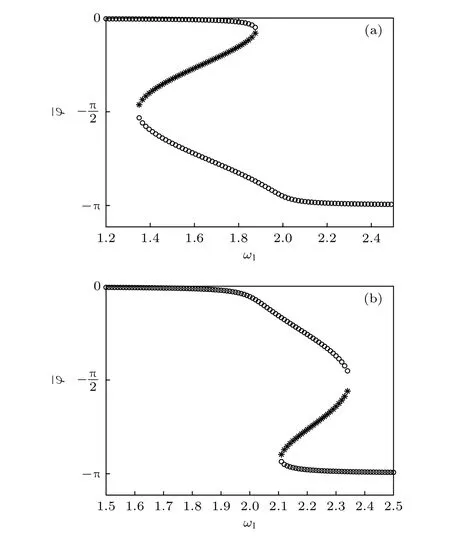
圖4 定常解的相頻曲線 (a) α 1=?0.4 , 剛度軟化; (b)α1=0.4, 剛度硬化(圓表示穩定解支, 星號表示不穩定解支)Fig.4.Phase-frequency curves of steady-state response:(a) α 1 = ? 0.4 , stiffness softening; (b) α 1 =0.4 , stiffness hardening (the circles for stable solution and the asterisks for unstable one).

當 ? =0 時, 未擾系統為Hamilton 系統:

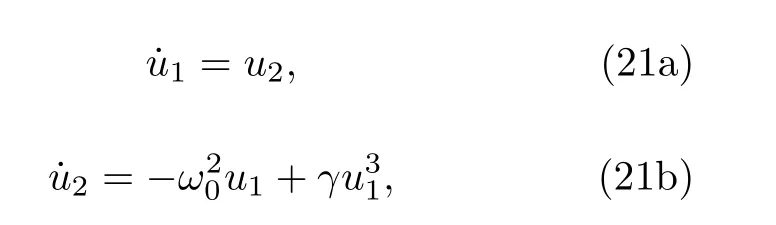
其Hamilton 量為

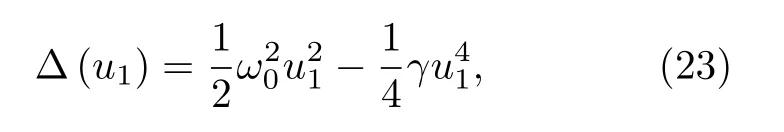
由于

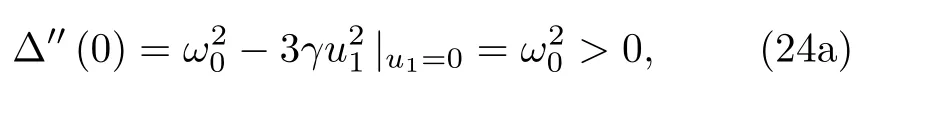
圖5 非線性系數 α 1 的影響 (a) 剛度軟化; (b) 剛度硬化 (圓表示穩定解支, 星號表示不穩定解支)Fig.5.Effects of the nonlinear coefficient α 1 : (a) Stiffness softening; (b) stiffness hardening (the circles for stable solution and the asterisks for unstable one).

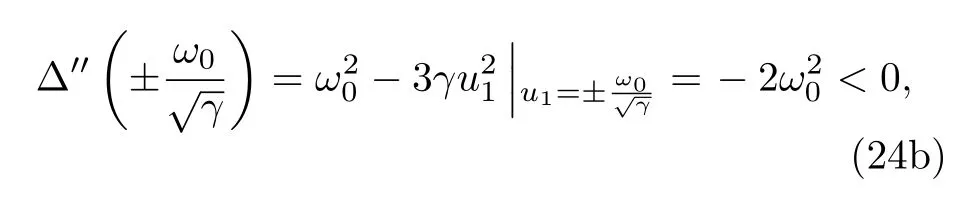
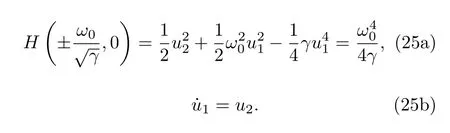
設 t =0 時, u1(0)=0 , 由 (25a)式 可以得到從而可以由(25)式解得 u1和 u2滿足:

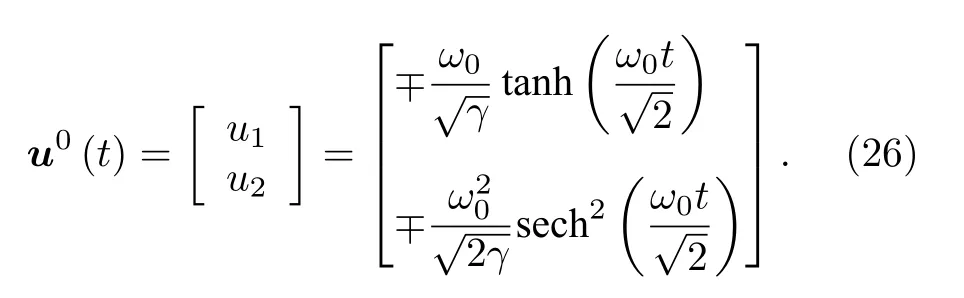
將(19)式寫成向量函數形式:

受擾系統(19)的Melnikov 函數為

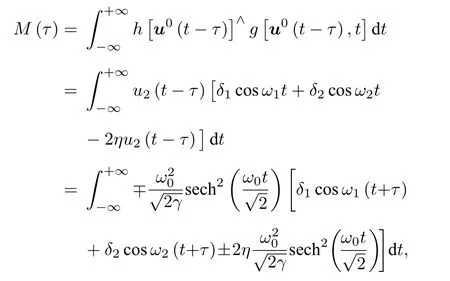
從而

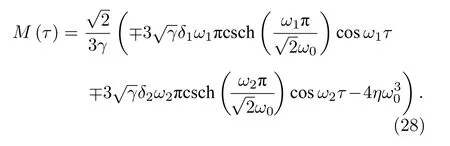
因此, 系統(1)出現異宿軌道橫截相交的必要條件是:

用原系統參數表示為

4.2 數值仿真

由(30)式可知, 對于剛度軟化的系統(1), 激勵 Fi越強、阻尼 c 越小和非線性剛度 α1越軟, 易于使系統的異宿軌道發生橫截相交, 從而系統(1)進入Smale 馬蹄意義下的混沌.由于激勵幅值 F1已限制為小量, 而 F2的選取較為自由, 因而考察 F2對系統動力學特性的影響.取系統參數 m =1 , c =0.3 ,k =1 , α1=?1 , F1=0.2 , ω1=1.1 , ω2=ω1/3 ,代入(30)式得到 F2>0.0623.即在上述的參數下,當 F2>0.0623 時系統(1)可能出現異宿軌道橫截相交, 并且 F2越大于此值, 系統越可能進入混沌.但該條件僅為系統進入混沌的必要條件, 還需進一步通過數值仿真才能得到系統進入混沌的臨界值.

在不同的激勵幅值 F2下利用自由插值的梯形方法[32,33]對系統(1)進行數值仿真, F2的起始值為 0.0600 , 初值為 ( u01,) = ( 0.208010172501537,0.326464098793873), 仿真時長為 t =200π/ω2, 步長為 2 ×10?4π/ω2.仿真得到系統的分岔圖如圖6所示.奇怪吸引子的相軌跡線在局部上總是以指數速率分離的, Lyapunov 指數通過度量相鄰相軌跡線分離或收斂的平均變化率判斷系統是否進入混沌, 是一種可靠的定量分析方法.利用Jacobian 法[34]計算得到這組參數下系統的最大Lyapunov 指數隨 F2變化的趨勢如圖7 所示.

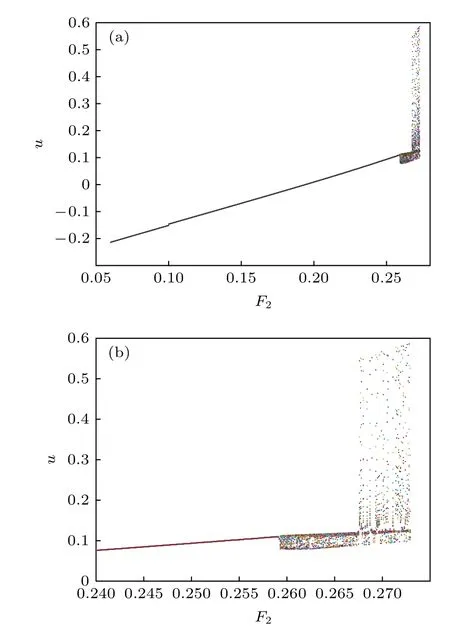
圖6 系統(1)隨 F 2 變化的分岔圖 (a) 整體圖; (b) 局部放大圖Fig.6.Bifurcation diagram of Eq.(1) changing with F 2 :(a) Panoramic view; (b) local enlarged view.

圖7 系統(1)的最大Lyapunov 指數隨 F 2 變化的趨勢 (a) 整體圖; (b) 局部放大圖Fig.7.The trend of the largest Lyapunov exponent of Eq.(1) changing with F 2 : (a) Panoramic view; (b) Local enlarged view.

圖8 F 2 =0.259 時的周期軌道Fig.8.Periodic orbits for F 2 =0.259.

從圖6 可見, 當 F2>0.259 時, 系統發生激變進入混沌態, 與圖7 中 F2>0.259 時最大Lyapunov指數的驟增吻合.取 F2=0.259 , 初值為 ( u02,) =( 0.110106001335058, 0.248137954024669) , 得到系統的周期軌道如圖8.取 F2=0.2595 , 初值為(u03,)= ( 0.091801856843936, 0.382525085869613),仿真得到系統的位移時間歷程、相軌跡和Poincare截面如圖9 所示.從圖8 和圖9 可見, 激勵幅值F2從 0.259 增加到 0.2595 時異宿軌道破裂, 周期軌道發展成為混沌吸引子, 系統的相軌跡受到左側鞍點吸引.此外, 從圖6 可見系統在 F2>0.268 時再次發生激變, 進入另一種混沌態.取 F2=0.268 , 初值為(u04,= (0.144691373245013, 0.202712823433900),仿真得到系統的位移時間歷程和相軌跡如圖10 所示, 這時系統的相軌跡被左右兩個鞍點吸引, 出現新的混沌吸引子.

圖9 F 2 =0.2595 時的混沌狀態 (a) Poincare 截面; (b) 位移時間歷程; (c) 相軌跡Fig.9.Chaotic state for F 2 =0.2595 : (a) Poincare map;(b) displacement time histories; (c) phase trajectory.

4.3 解析結果與數值仿真結果的關系

在前述的系統參數下, 通過Melnikov 方法解析得到激勵幅值 F2的臨界值為 0.0623 , 通過數值仿真得到系統首次出現混沌的臨界值為 0.259.為進一步研究解析與數值仿真得到的臨界值的關系, 仍取系統參數 m =1 , c =0.3 , k =1 , α1=?1 , F1=0.2 ,并且激勵頻率保持嚴格的倍數關系 ω1=3ω2, 分別利用數值仿真和Melnikov 方法解析求解不同的頻率組合下 F2的臨界值, 得到仿真結果與解析結果的對比如圖11(a)所示.

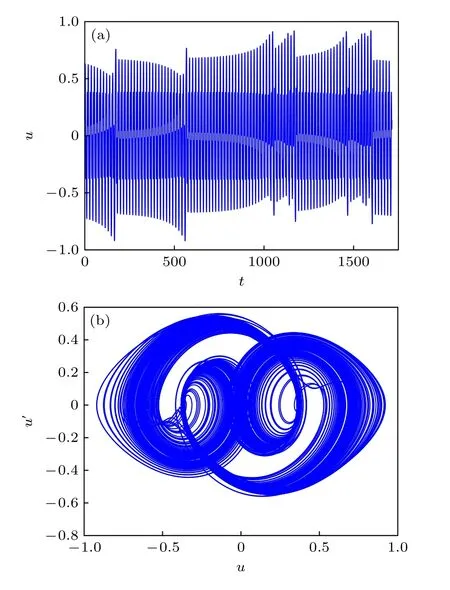
圖10 F 2 =0.268 時的混沌狀態 (a) 位移時間歷程; (b) 相軌跡Fig.10.Chaotic state for F 2 =0.268 : (a) Displacement time histories; (b) phase trajectory.

然后考察激勵頻率為近似倍數關系ω1≈3ω2的情況.其他參數不變, 并且固定 ω1=1.1 , 求解不同的激勵頻率 ω2下系統出現混沌的臨界激勵幅值F2, 得到解析與數值仿真結果對比如圖11(b)所示.再固定 ω2=0.3667 , 求解不同的激勵頻率ω1下系統出現混沌的臨界激勵幅值 F2, 得到結果如圖11(c)所示.

從圖11 可見, 解析結果能夠大致反映 F2的臨界值的趨勢, 與仿真結果僅在數值上存在差異, 原因是Melnikov 方法解析得到的臨界值僅為系統進入混沌的必要條件, 系統的激勵幅值 F2需大于該臨界值到一定程度才能首次進入混沌.此外, 從圖11(a)和圖11(c)可見, 系統在激勵頻率滿足嚴格的倍數關系和近似的倍數關系這兩種情況下, 臨界值的變化趨勢大致相同.

5 結 論

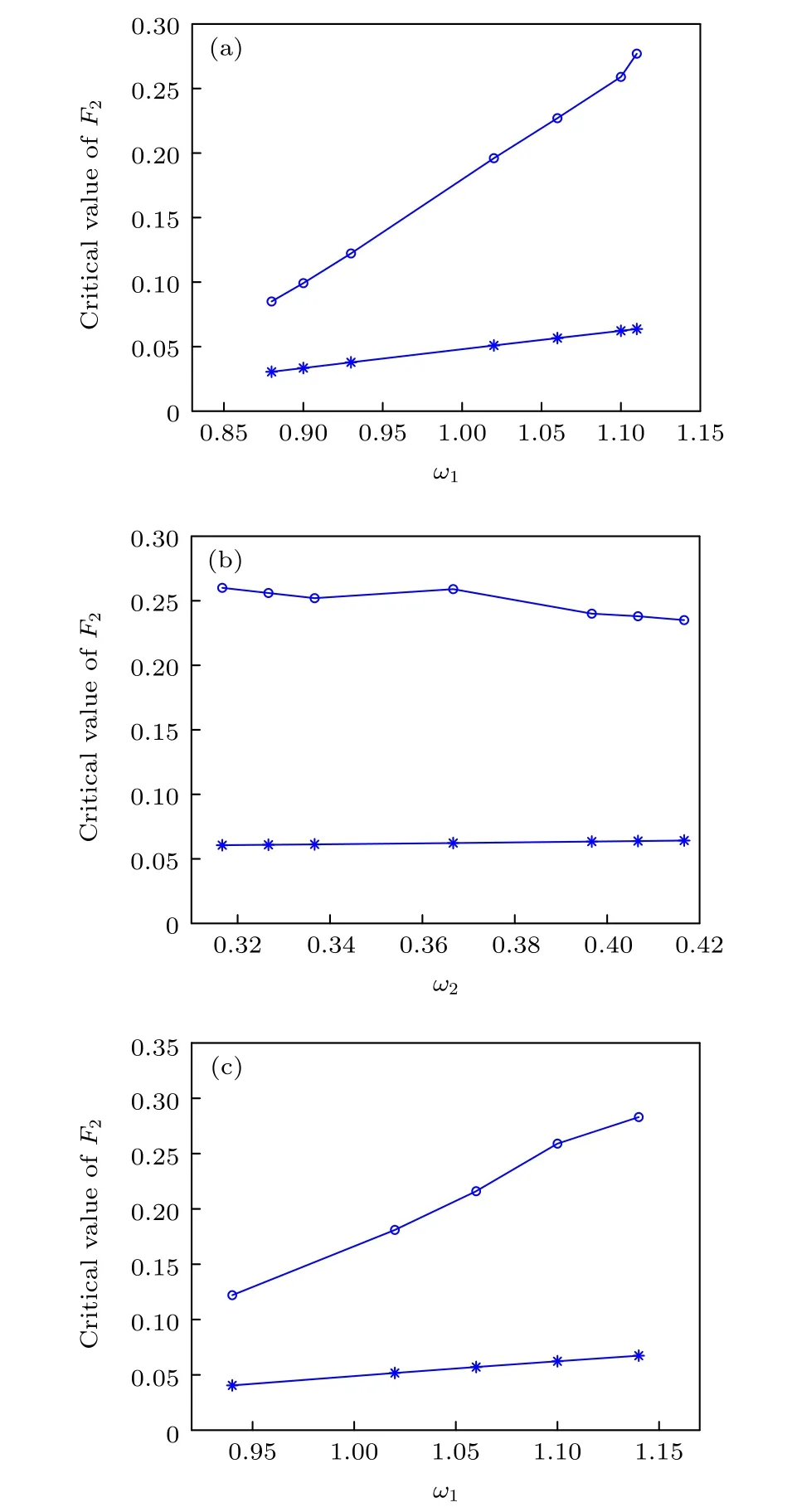
圖11 臨界激勵幅值 F 2 的解析結果與數值仿真結果對比 (a) ω 1 =3ω2 ; (b) ω 1 =1.1 ; (c) ω 2 =0.3667 (星 號代表解析結果, 圓代表數值仿真結果)Fig.11.Comparisons of analytical results and numerical simulation results of critical excitation amplitude F 2 : (a)ω1 =3ω2 ; (b) ω 1 =1.1 ; (c) ω 2 =0.3667 (the asterisks for analytical results and the circles for numerical simulation results).

應用多尺度法得到Duffing 系統的主-超諧聯合共振的近似解析解, 并用數值方法進行驗證, 解析解的瞬態過程和穩態過程都具有較高精度.基于Lyapunov 第一方法研究了系統穩態周期運動的穩定性, 發現系統最多存在2 個穩定解支和1 個不穩定解支.討論了非線性剛度對穩態周期運動的幅頻響應的影響, 結果表明非線性剛度硬化和軟化均能夠降低響應的幅值, 并且剛度軟化能夠進一步影響響應的多值性.基于Melnikov 方法對剛度軟化系統進行全局分析, 得到系統的異宿軌道橫截相交的必要條件, 發現較大的激勵幅值、小阻尼和剛度軟化容易使系統進入混沌.選取一組符合主-超諧聯合共振條件的參數進行數值仿真, 發現兩個臨界值.當激勵幅值通過第一個臨界值時, 系統的異宿軌道破裂, 以激變方式進入混沌態; 激勵幅值通過第二個臨界值時, 系統再次發生激變, 出現新的混沌吸引子.對多種頻率組合的參數分別利用數值仿真和Melnikov 方法解析得到系統首次進入混沌的臨界值, 對兩種方法所得結果進行了對比, 解析結果在一定程度上能夠真實反映系統的臨界值變化的趨勢, 數值仿真的結果也驗證了解析結果的正確性.