量子真空計量標準中的非極性稀薄氣體折射率測量研究*

范棟 習振華 賈文杰 成永軍 李得天

(蘭州空間技術物理研究所真空技術與物理重點實驗室, 蘭州 730000)

為進一步提高真空量值的復現性和準確性, 最新研究采用量子技術實現對真空量值的測量與表征.該方法利用Fabry-Perot 諧振腔實現腔內氣體折射率的精密測量, 并反演出氣體密度, 進而獲得對應的真空量值,其中氣體折射率的測量是影響真空量值準確性的關鍵.本文基于第一性原理, 利用從頭計算理論計算了在已知壓力和溫度條件下的氦氣折射率, 給出腔內氣體壓力與折射率關系的表達式, 并利用基于Fabry-Perot 激光諧振腔的真空測量裝置, 通過雙腔諧振激光拍頻精確測量了充氣前后諧振激光頻率的變化, 測出了氦氣折射率, 并分析了測量不確定度.將理論計算值與實驗測量值進行了對比分析, 得出了制約準確度提高的主要因素, 并提出了修正方法.

1 引 言

2018 年, 國際單位制(International System of Units, SI)中7 個基本量全部由物理常數定義[1].面對國際計量體系的歷史性變革, 諸多計量參數對應的基于經典物理學的實物標準向“自然標準”即量子標準發展, 利用量子躍遷等現象復現計量單位, 用相同裝置實現任何時間、任何地點量值復現,消除宏觀參數不穩定產生的影響, 將準確度提高數個量級.目前, 時間、長度、電學等方面的量子基準已逐步建立.與此同時, 采用光學干涉、冷原子碰撞損失、吸收光譜等基于物質本征物理性質復現真空量值的新方法、新概念具備突破傳統技術性能極限的應用潛力, 可在多個地點及不同時間復現真空量值, 已成為國際上新的研究熱點[2].其中, 基于Fabry-Perot(F-P)激光諧振腔測量非極性稀薄氣體折射率, 進而反演真空度的測量方法為替代水銀壓力計—真空量值基準提供了可能.該方法在減小測量不確定度的同時, 可實現真空量值的扁平化傳遞, 為真空量值提供了新的溯源途徑[3?5].近年來, 美國國家標準與技術研究院(NIST)、瑞典于默奧大學(Ume? universitet)和日本國家先進工業與技術研究所(AIST)等對基于F-P 激光諧振腔測量折射率反演真空度的真空測量技術進行了研究[6?9], 該技術主要面臨的挑戰是由于溫度和充氣導致諧振腔腔長變化, 從而影響折射率的測量準確度[10].國內此類研究尚屬起步階段[11,12].

量子動力學將非極性氣體宏觀介電常數與原子微觀極化參數相聯系.近年來, 量子力學關于單原子分子(氦氣、氬氣等)電磁學性質和熱力學性質從頭計算(ab initio)理論及方法的迅速發展, 相關參數的計算精度不斷提高(例如, He 的摩爾極化率理論計算相對不確定度達到 2 × 10–7), 可進一步減小上述方法的測量不確定度[13?20].

本文采用基于F-P 激光諧振腔的真空測量裝置開展非極性稀薄氦氣折射率反演真空量值研究,對比理論計算折射率與測量折射率, 并評定各不確定度分量及權重系數, 分析制約準確度提高的主要因素并提出修正方法.

2 折射率理論計算

氦氣是除氫氣以外最簡單的氣體原子, 因此其微觀物理參量可以達到最高精度的計算.在折射率理論值的計算過程中, 首先對氦原子的摩爾極化率、摩爾磁化率、第二維里系數和第二介電維里系數進行計算.原子極化率可以寫為波長的展開式:

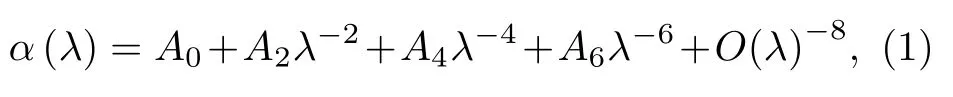
式中, λ 為激光波長(單位為?), α 為原子極化率(原子單位制), A0為靜極化率, Ak( k =2,4,6 )為極化率色散系數, 其值如表1 所示.

表1 He 極化率的展開系數(原子單位制)[17]Table 1.Cofficients in the expansion of the polarizability of Helium.

在激光波長λ = 780 nm 時, 計算得出He 極化 率α(780 nm) = 2.0583140283 × 10–25cm3.由于原子磁化率χ 比原子極化率α 小5 個數量級,因此可忽略χ 的色散修正, 只需考慮其靜態成分,靜態磁化率χ = –3.14062677086 × 10–30cm3[21].為使氣體密度以mol/cm3為單位, 需將α 和χ 轉化為摩爾極化率A?= 4πNAα/3 和摩爾磁化率Aμ=4πNAχ/3, 其中, NA為阿伏伽德羅常數.經計算,A?= 0.5192196805 cm3/mol, Aμ= –0.0000079224 cm3/mol.

根據Bich[19]和Rizzo[20]公布的各溫度點下第二維里系數和第二介電維里系數的值, 對其進行擬合, 在250—350 K 溫度范圍內, 得出第二維里系數B(T)和第二介電維里系數B?(T)關于溫度的線性表達式:

式中T 為溫度.在溫度T = 299.1485 K 時, 可得B(T)=11.818 cm3/mol,B?(T)=–0.053 cm6/mol2.

氣體壓力(單位為Pa)和密度(單位為mol/m3)的關系可通過維里狀態方程來表示:

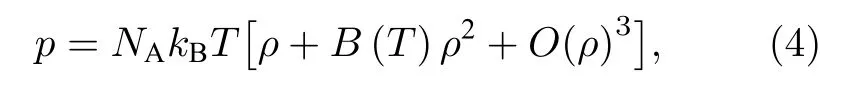
式中, p 為氣體壓力, NA為阿伏伽德羅常數, kB為玻爾茲曼常數, T 為溫度, ρ 為氣體密度, B(T)為第二維里系數.

可通過Lorentz-Lorenz 方程建立氣體密度與折射率的聯系, 用摩爾極化率、摩爾磁化率(以cm3/mol 為單位)及第二介電維里系數表示氣體密度(以mol/cm3為單位), 有:

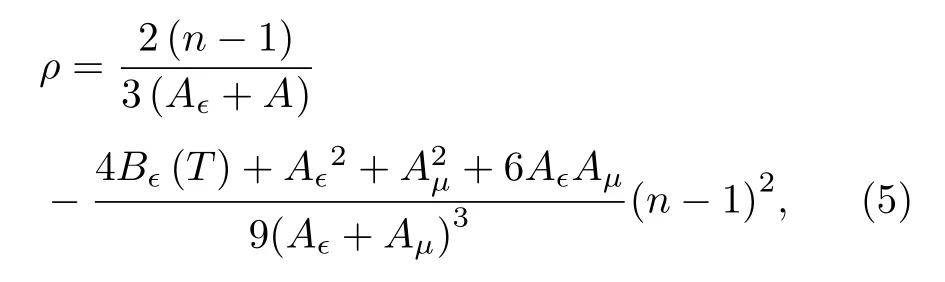
式中, ρ 為氣體密度, n 為氣體折射率, A?為摩爾極化率, Aμ為摩爾磁化率, B?(T)為第二介電維里系數.

結合(4)式和(5)式, 可得到壓力與折射率的關系:

(6)式中, 各項系數表達式分別為:

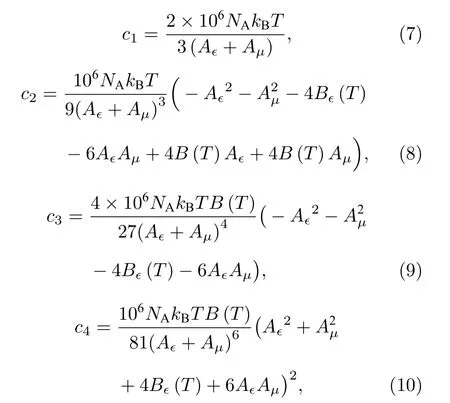
式中, NA= 6.02214076 × 1023mol–1, kB= 1.380649 ×10–23J/K, T = 299.1485 K.計 算 得 出, c1=3.19363 × 109; c2= 4.83514 × 1010; c3= –3.32951 ×109; c4= 5.71882 × 107.在p = 100166 Pa 時, 第二項分別比第三項和第四項高5 和7 個數量級, 因此在計算折射率時, 可忽略第三項和第四項.則反寫(6)式可得出折射率關于壓力的簡化表達式:

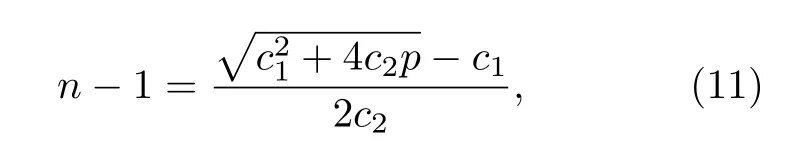
根據(11)式, 即可通過A?、Aμ、B?(T)、B(T)以及壓力和溫度計算出氦氣折射率, 其結果如表2所示.

根據表2 所示的結果, 對折射率計算不確定度進行分析.(6)式中, 由于摩爾極化率比摩爾磁化率高5 個數量級, 且在p = 100166 Pa 時, 第一項比第二項高4 個數量級, 因此可忽略折射率非線性高階項和摩爾磁化率對折射率計算不確定度的影響.則(6)式可簡化為折射率n 的計算表達式:

式中, p 為已知氣壓值.

(12)式中, A?的相對不確定度ur, A?= 2 × 10–7,修正后的SI 中, kB和NA沒有不確定度[22], 折射率計算的相對不確定度為 ur,n1.經分析可知, 當壓力點為105Pa 時, 其折射率計算不確定度最大, 隨著氣壓降低, 不確定度逐漸減小, 因此選取不確定度最大的點作為不確定度評定點.真空度p =100166 Pa 時, 利用(13)式進行折射率計算不確定度分析:

式中, uc,n1為折射率理論值n 的標準不確定度,uc,A?為摩爾極化率的標準不確定度.

分析得出, 折射率理論值n 的相對不確定度ur,n1=6.27×10?12.

3 實驗原理與方法

3.1 實驗裝置與原理

本文所用實驗裝置結構如圖1 所示, 探測激光器為兩個中心波長為780 nm 的外腔室式半導體激光器(ECDL, TOPTICA, DL pro).腔體材料為超低熱膨脹玻璃(ULE), 采用雙腔結構.通過調節透鏡組進行模式匹配, 之后使用信號發生器(RIGOL,DG4102)發出的正弦同步信號對電光調制器(EOM,THORLIBS, CRDS)進行相位調制, 使透射信號出現邊帶.然后利用信號發生器產生的同頻信號和腔內反射信號混頻產生誤差信號, 通過誤差信號利用PDH(Pound Drever Hall)鎖頻裝置將激光鎖定在腔縱模上, 并利用頻率計(KEYSIGHT, 53220A)測量兩組激光的拍頻.真空泵組包括機械泵(Leybold, SCROLLVAC)、分子泵(Leybold, TURBOVAC)和離子泵(Gamma Vacuum, TiTan lon Pump), 先用機械泵抽氣實現粗真空, 再同時打開分子泵進一步抽氣提高真空度, 當抽氣至所需真空度時, 打開離子泵進行真空度維持.氣瓶后連接一個液氮冷阱, 可去除雜氣, 氣體通過微漏閥控制流速進入腔體, 腔體外部連接電容薄膜真空計(INFICON Cube CDGSci)以檢測充氣壓力.

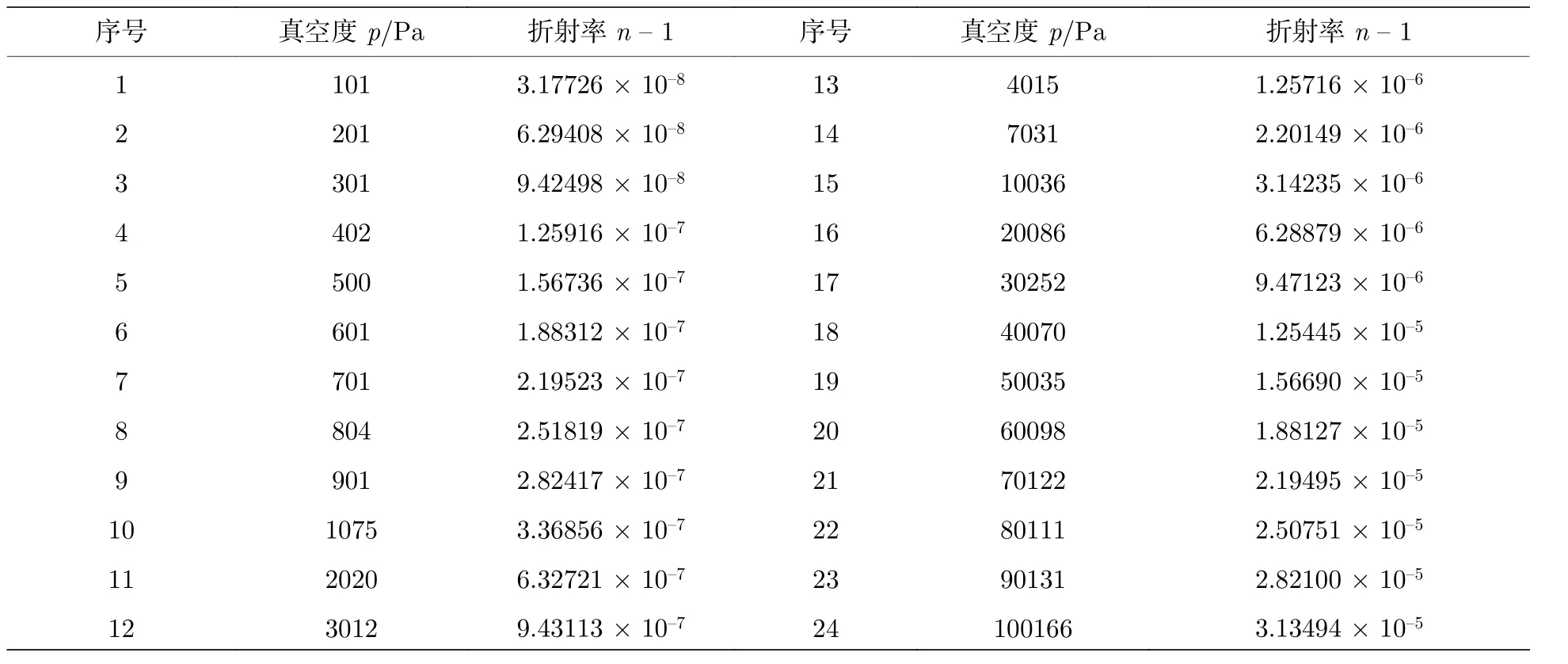
表2 折射率計算結果Table 2.Calculation results of refractive index.

圖1 基于F-P 激光諧振腔的真空測量裝置結構圖 (a)部分為光路圖;(b)部分為氣路圖 (1.激光器; 2.分束光纖; 3.激光準直器; 4.1/2 波片; 5.格蘭棱鏡; 6.透鏡組; 7.電光調制器; 8.光隔離器; 9.偏振分光棱鏡; 10.1/4 波片; 11.高反鏡; 12.透鏡; 13.光電放大探測器; 14.PDH 鎖頻裝置; 15.光電探測器; 16.頻率計; 17.檢測腔; 18.參考腔; 19.電容薄膜真空計; 20.氣瓶; 21.冷阱; 22.離子泵; 23.電離規; 24.分子泵; 25.機械泵.紅色實線為光路; 黑色實線為光纖; 黑色虛線表示反饋作用; 藍色實線為氣路.)Fig.1.Structure diagram of vacuum measuring device based on F-P cavity.

激光鎖定在F-P 腔縱模上時, 腔內激光諧振頻率可表示為

式中, q 為整數, c 為真空中的光速, n 為氣體折射率, L0為諧振腔長度.

將充氣前后的諧振腔內頻率值代入(14)式求差, 即可推導出絕對氣體折射率n 的表達式:

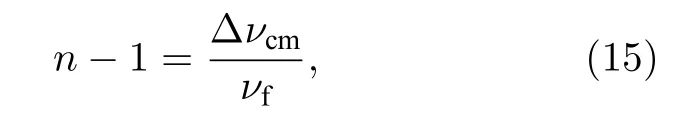
式中, ?νcm為腔內諧振激光頻率的變化, νf為檢測腔內諧振激光末態頻率.

考慮到充氣過程中激光縱模模數變化和氣體壓力對腔體長度的影響, (15)式可寫為

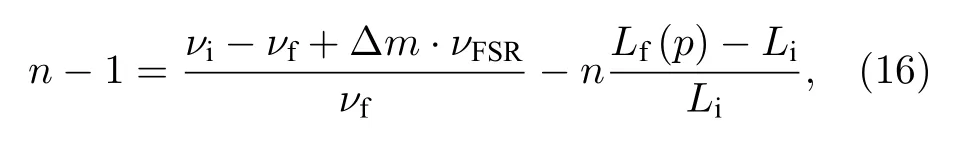
式中, νi為檢測腔諧振激光初態頻率, νf為檢測腔諧振激光末態頻率, Δm 為檢測腔內諧振激光縱模模數變化量, νFSR是自由光譜范圍, Lf(p)為充氣后腔體實際物理長度, Li為充氣前腔體物理長度.

(16)式中第二項長度變化因子Lf(p)和Li主要是由于充氣后氣體壓力導致的腔長變化:

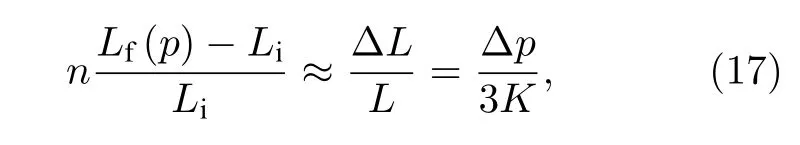
式中, ?p 為腔內氣壓變化量, K 為ULE 材料的體積模量.

在腔體高真空(n = 1)狀態下測量諧振激光初態頻率νi, 腔體中充入一定壓力的氦氣時測量諧振激光末態頻率νf, 即可得到充氣壓力點下的頻率差?νcm, 最后代入(16)式計算出每個頻率差對應的氣體壓力.

3.2 折射率測量方法

為準確測量諧振腔內氣體折射率, 利用PDH鎖頻模塊將激光頻率鎖定在諧振腔內, 并通過SRS溫度監測模塊及Pt100 鉑電阻將諧振腔內溫度控制在ULE 材料的零膨脹溫度點299.1485 K.首先將檢測腔和參考腔分別抽氣至10–5Pa, 并測量初態拍頻和檢測腔內諧振激光初態頻率; 其后將檢測腔充氣至各壓力點, 并測量末態拍頻和檢測腔內諧振激光末態頻率.則結合(16)式和(17)式可得出折射率計算表達式:

式中, νr為參考激光頻率, νbeati為充氣前兩束激光拍頻, νbeatf為充氣后兩束激光拍頻.

利用(18)式得到折射率測量結果如表3 所示.

根據表3 所示的結果, 對折射率測量不確定度進行評定分析.由于(18)式中, 分量的不確定度量級為10–15, 故可以忽略不計.經分析后發現當測量壓力點為101.5 Pa 時, 氣體折射率n – 1 =3.93406 × 10–8, 其測量不確定度最大, 隨著腔內氣體壓力增大, 其測量不確定度逐漸降低, 因此選取該點作為氣體折射率測量不確定度評定點.在折射率測量不確定度評定過程中, (18)式可寫為

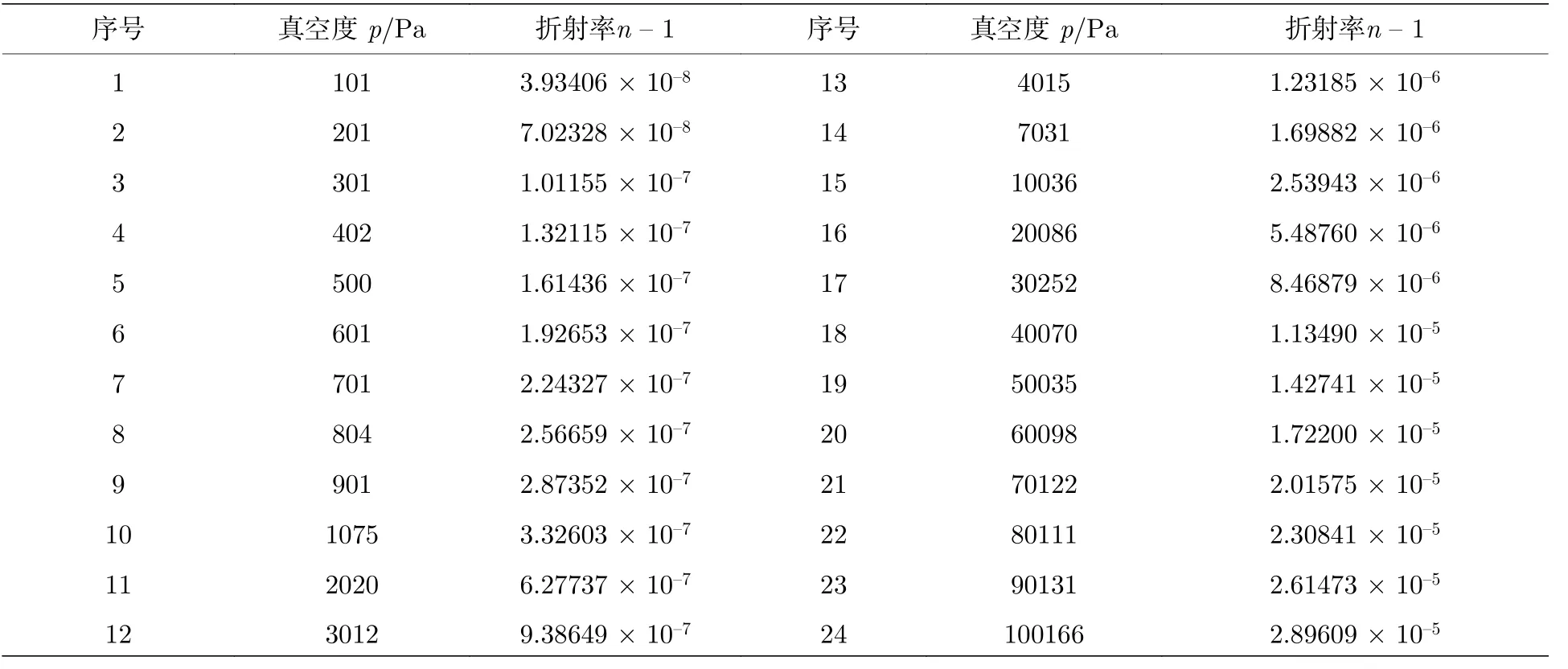
表3 折射率測量結果Table 3.Text results of refractive index.

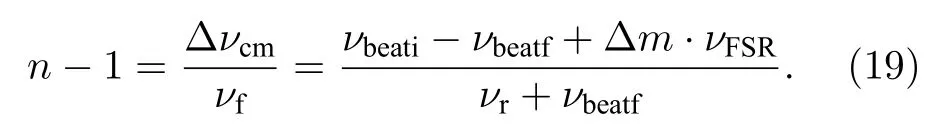
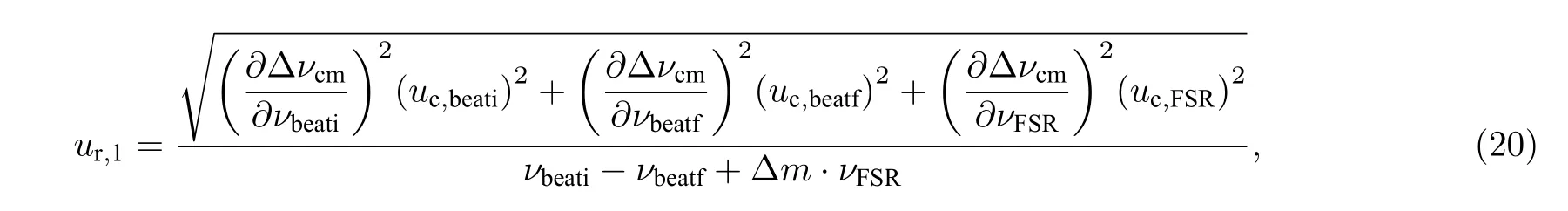
(19)式中, 分子部分為充氣前后檢測腔諧振激光頻率變化量, 其相對不確定度為ur,1, 分母部分為檢測腔末態諧振激光頻率, 其相對不確定度為ur,2, 折射率測量不確定度為 ur,n2.實驗中, 參考激光頻率νr和自由光譜范圍νFSR用波長計測量, 其裝置測量不確定度uc,r和uc,FSR均為10–6; 初態拍頻νbeati和末態拍頻νbeatf用頻率計測量, 其裝置測量不確定度uc,beati和uc,beatf均為10–6; 不確定度評定方法如下:

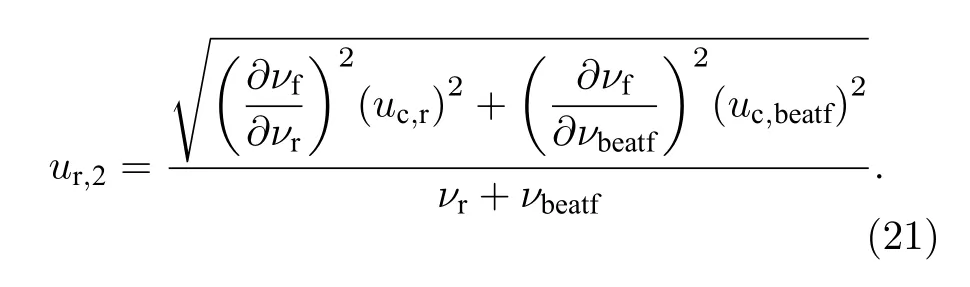
(19) 式中各項參數的數值分別為: νFSR=1497.9916 MHz; ?m = 0; νr= 384366590 MHz;νbeati= 1420 MHz; νbeatf= 1434, 74 MHz.經 評定, 分子部分的測量不確定度ur, 1= 9.59 × 10–8,分母部分的測量不確定度ur, 2= 3.68 × 10–15, 各分量相互獨立且不相關, 由(22)式:

可計算出當氣體壓強為101.5 Pa 時, 其折射率測量不確定度 ur,n2=9.59×10?8.

4 分析與討論

結合第2 節和第3 節得到的折射率理論和測量結果, 對折射率與檢測腔內真空度之間關系進行對比分析, 其結果如圖2 所示.

圖2(a)顯示腔內氦氣壓力在102—103Pa 范圍內, 氦氣的折射率測量值大于理論值, 其主要原因是腔體材料中有余氦, 在腔內氣壓較低時, 腔體對氦的吸氣速率小于放氣速率, 因此由氦氣脫附引起腔內氦氣量增多, 導致了折射率測量值偏大, 這驗證了ULE 材料存在滲氦現象[23].圖2(b)顯示腔內氦氣壓力在103Pa 附近時, 氦氣折射率測量值開始小于理論值, 并且隨著腔內氣壓增大, 氦氣折射率測量值與理論值偏差也逐漸增大(偏差值從4.25267 × 10–9到2.38851 × 10–6), 其主要原因是隨著氦氣壓力增大, 腔體滲氦量增加, 并且滲氦和返氦速率均增大, 但腔體對氦的吸氣速率大于放氣速率, 導致折射率偏差逐漸增大.圖2(c)顯示腔內壓力在102—105Pa 范圍內, 氦氣折射率理論值與測量值偏差隨腔內氣壓的總體變化情況.

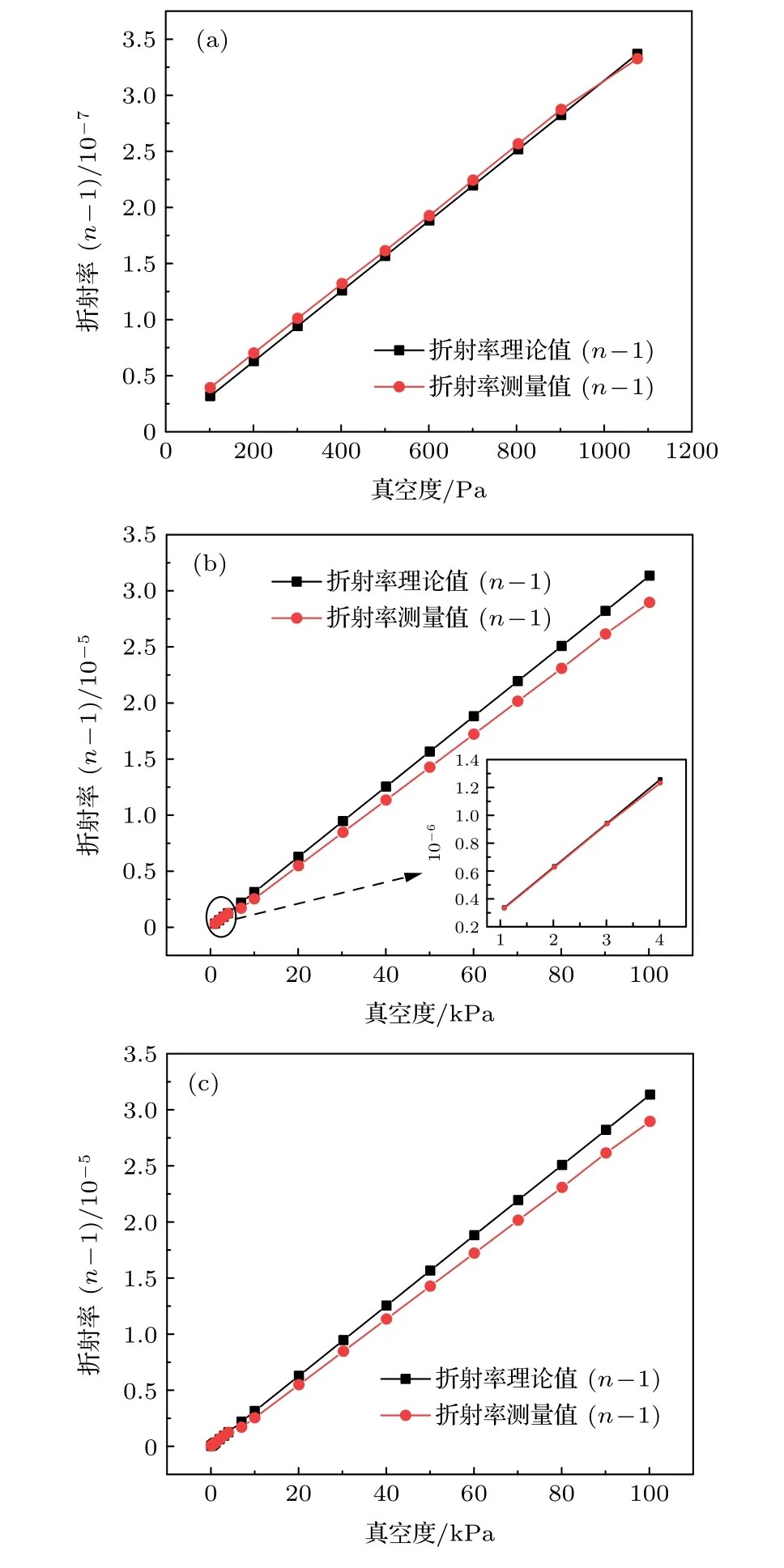
圖2 (a)102?103 Pa 范圍內折射率理論值與測量值對比圖; (b) 103?105 Pa 范圍內折射率理論值與測量值對比圖;(c) 102?105 Pa 范圍內折射率理論值與測量值總對比圖Fig.2.(a) Comparison between theoretical and measured values of refractive index in the range of 102?103 Pa; (b) comparison between theoretical and measured values of refractive index in the range of 103?104 Pa; (c) total comparison between theoretical and measured values of refractive index in the range of 102?105 Pa.

分析表明, 在利用基于F-P 激光諧振腔的真空測量裝置測量氦氣折射率實現新的真空標準中,由于ULE 材料滲氦導致腔體長度變化對折射率測量不確定度的影響較大.為降低此影響, 需對測量結果引入必要的腔長修正.由于折射率測量不確定度在10–8量級, 此量級下無法根據已知的ULE 材料特性計算出充氣前后腔長的變化, 所以可利用氦氣折射率的理論計算值來量化由滲氦所致腔體形變導致的測量折射率偏差.充氣后, 諧振腔實際物理長度為

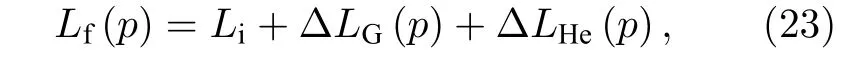
式中, Lf(p)為充氣后腔體實際物理長度, Li為充氣前腔體物理長度, ?LG(p)為氣體壓力導致的腔長變化量, ?LHe(p)為腔體滲氦導致的腔長變化量.Lf(p), ?LG(p), ?LHe(p)是壓力的函數.

將(23)式代入(14)式和(16)式得到加腔長修正后的折射率表達式:

式中, ?νcm為激光諧振頻率變化量, φ(p)為與腔體滲氦相關的折射率修正系數:

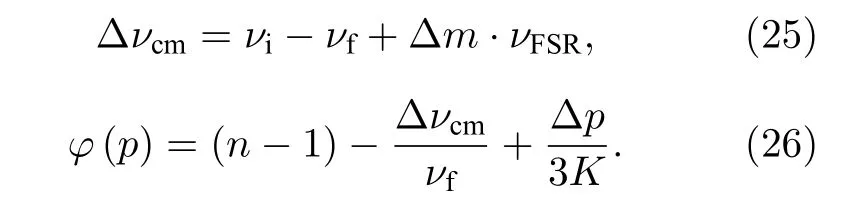
根據本文得到的折射率理論值和計算值, 即可計算出103—105Pa 真空度范圍內本實驗所用實驗裝置的折射率修正系數, 如表4 所示.

對表4 中數據進行擬合, 得到: 在1075—7031 Pa壓力范圍內, 折射率修正系數關于腔內氣壓的表達式為

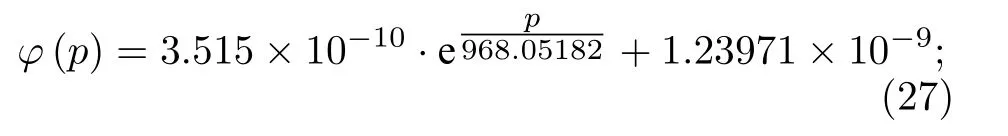
在7031—100166 Pa 壓力范圍內, 折射率修正系數關于腔內氣壓的表達式為

為了進一步量化由氣體壓力導致的諧振腔腔長變化, 可以推導出氣體壓力所致腔體相對變化量關于折射率的表達式.氣體壓力所致腔體形變量關于氣體壓力的表達式為

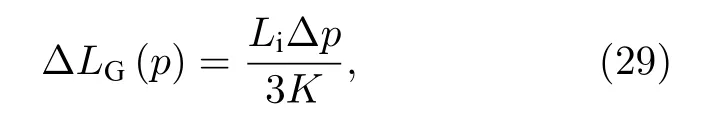
式中, Li為充氣前腔體的物理長度, p 為氣體壓力,K 為ULE 材料的體積模量.則氣體壓力所致腔體相對變化量為

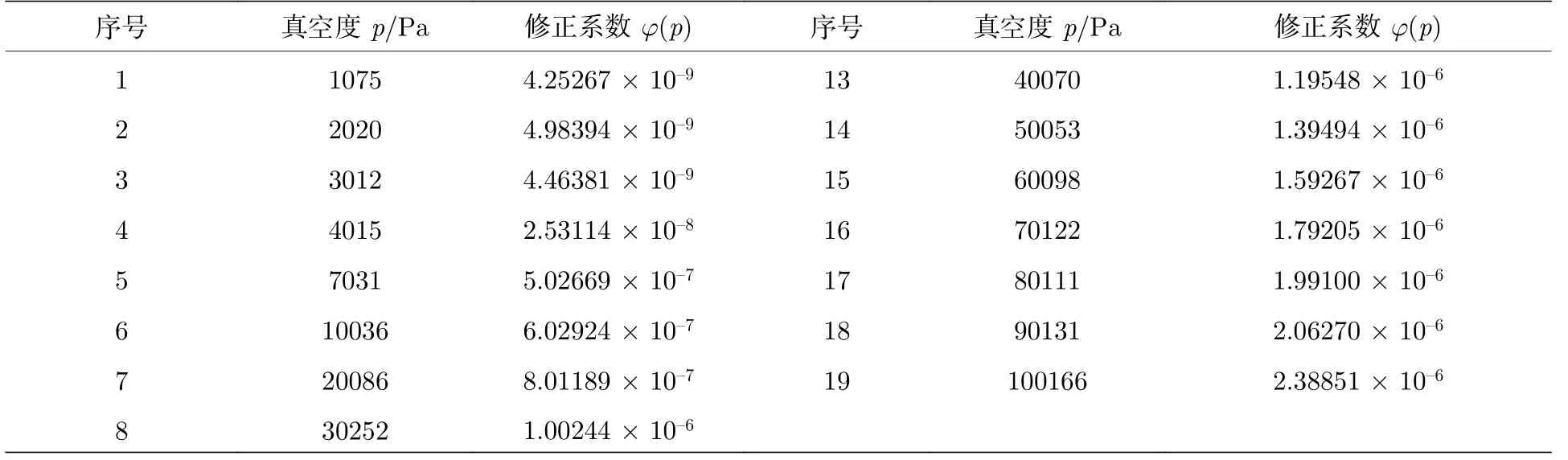
表4 折射率修正系數Table 4.Refractive index correction coefficient.

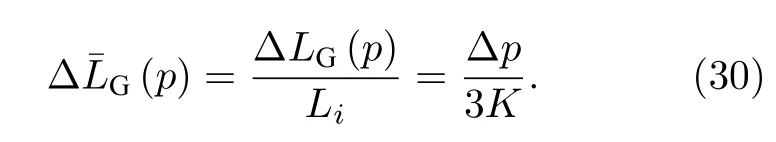
將(30)式代入(4)式和(5)式中的壓力和密度的一階線性項, 并忽略密度一階表達式中摩爾磁化率的影響, 即可得到氣體壓力所致腔體相對變化量關于折射率的表達式:

令:

式中, K 為ULE 材料的體積模量.

則可得出, 充氣后氣體壓力所致腔體相對變化量關于折射率的表達式為

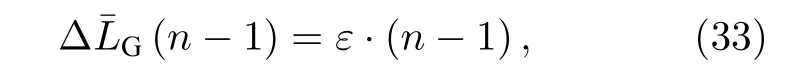
式中, ε 是無量綱腔長修正參數, 在本實驗條件下,其值為3.12 × 10–2.

5 結 論

本文首先在壓力和溫度已知的情況下, 基于第一性原理利用摩爾極化率、摩爾極化率和維里系數等微觀物理參量對氦氣折射率理論值完成精確計算, 得出腔內氣體壓力與折射率關系的表達式并分析得出折射率理論值的相對不確定度為6.27 ×10–12.其后利用基于F-P 激光諧振腔的真空測量裝置, 對102—105Pa 范圍內的氦氣折射率進行測量, 評定其測量不確定度為9.59 × 10–8.最后對氦氣折射率理論值和測量值對比分析, 得出氦氣折射率測量不確定度的主要原因是由滲氦引起的諧振腔腔體形變, 因此解決滲氦問題是建立新的真空標準的關鍵.文中對氦氣折射率測量中由腔體滲氦導致的腔長變化進行了修正, 得到103—105Pa 真空度范圍內各壓力點下的折射率修正系數及其關于腔內氣壓的表達式, 并進一步量化氣體壓力導致的腔長變化量, 得到氣體壓力所致腔體相對變化量與折射率的關系, 計算出腔長修正參數ε = 3.12 ×10–2.在以后利用F-P 諧振腔的氦氣折射率測量實驗中, 可利用本文所給的各壓力點下的折射率修正系數對折射率測量結果進行修正, 消除腔體滲氦對折射率測量的影響, 從而得到高準確度的氣體壓力.隨著量子力學關于單原子分子電磁學性質和熱力學性質從頭計算理論及方法的迅速發展, 相關參數計算精度提高, 將來可利用其他非極性氣體(如氖)實現氣體折射率至氣體壓力的精確反演, 降低由于氣體擴散導致的折射率測量不確定度, 實現真空計量新標準.