四穩系統的雙重隨機共振特性*
俞瑩丹 林敏 黃詠梅 徐明
(中國計量大學計量測試工程學院, 杭州 310018)
提出了一類8 次勢函數并討論了其分岔特性, 得到由左、右2 個小尺度雙穩勢和中間勢壘構成的對稱四穩系統.建立了在周期力和隨機力共同作用下四穩系統輸出響應的近似解析表達式, 并從能量角度引入功這一過程量來刻畫大、小不同尺度雙穩勢之間的作功能力, 發現四穩勢中存在著雙重隨機共振現象.理論分析與數值仿真結果表明, 當中間勢壘高度大于左右2 個小尺度雙穩勢的勢壘高度時, 四穩系統的響應隨著噪聲強度的變化由束縛在小尺度雙穩系統中做小幅振動轉變為跨越中間勢壘的大幅振動, 功隨噪聲強度的變化出現了雙峰曲線, 存在著雙重隨機共振, 且小尺度隨機共振能增強大尺度隨機共振的效應.
1 引 言
隨機共振(stochastic resonance, SR)是1981年由Benzi 等[1]在研究周期性回歸冰川期問題時提出的.經過30 多年的深入研究, SR 的內涵[2?5]不斷擴展, SR 的應用領域[6?10]也不斷拓寬.SR 將單一頻率的有序周期運動與噪聲的極度無序運動聯系在一起, 展示了周期性和隨機性之間的合作效應實際上是可能的, 表明噪聲可以提高系統響應中的周期性程度, 并在一定的條件下增大了響應的幅度.
雙穩系統[11?14]是研究SR 的經典模型, 人們相繼研究了耦合雙穩[15]、分段線性雙穩[16]、指數型雙穩[17]等雙穩類系統, 分別采用將兩個雙穩系統通過非線性方式耦合為一個多穩態系統, 將經典雙穩勢函數的內外側改為一次的線性形式和將二次項和指數項結合構成指數型雙穩系統的方式來改變經典雙穩系統的結構, 豐富其動力學特性的同時也提升了雙穩SR 的性能.近年來, 人們又相繼研究了對稱三勢阱[18?21]、非對稱三勢阱[22]、復合三穩[23]等三穩類系統, 這些研究表明在由三個勢阱和兩個勢壘構成的三穩系統中, 粒子每周期來回運動躍遷次數增加, 噪聲與非線性的作用也加強了,這有助于提高噪聲利用率; 且由高斯勢模型與混合雙穩模型結合構成的復合三穩系統因保留了高斯勢模型和能獨立調整中間勢阱的形態, 其性能優于三穩系統.因此, 非線性勢函數結構對SR 效應具有重要影響, 而增加穩態個數是改變結構的方法之一.
1997 年, Vilar 和Rubi[24]提出一類復合系統模型, 并發現此類系統的輸出信噪比可在不同的噪聲值處呈現出多個極大值, 從而產生多重SR 現象,這引起了學者們的廣泛關注.此后, 研究人員相繼在余弦信號和高斯噪聲驅動下的雙穩系統[25]、余弦信號和色噪聲驅動下的雙穩系統[26]及周期矩形信號和色噪聲共同作用下的時滯非對稱雙穩系統[27]中都發現了多重SR 現象.然而, 這些研究側重于分析系統的特征參量(如噪聲強度、噪聲關聯時間和關聯強度等)對SR 的影響, 并未對多個共振峰之間的關系展開研究, 也未涉及SR 效應的增強與控制.
動力學系統的共振是由作用到系統的外力激發的, 不同類型的外力導致各自獨特的共振狀態,而共振效應的強弱可用振動幅度的大小或具有的作功能力來度量.噪聲與非線性的作用主要體現在勢壘的躍遷上, 從雙穩到三穩既增加了穩態的個數也增加了可躍遷的勢壘個數, 用作功[28,29]這一過程量更能細致刻畫SR 過程中的能量變化.如何提高非線性振動系統的響應能力, 將噪聲作為一種重要的動力學因素, 增強噪聲與非線性相互作用產生的SR 效應是近年來人們關注的研究熱點.
鑒于目前的研究都是圍繞雙穩系統和三穩系統展開且發現三穩系統的性能優于雙穩系統, 本文研究了四穩系統的SR 現象.提出一類8 次勢函數并討論了其分岔特性, 得到由左、右2 個小尺度雙穩勢和中間勢壘構成的對稱四穩系統.根據絕熱近似理論[30], 推導了四穩系統在周期力和噪聲力協同作用下的輸出響應的近似解析表達式, 并引入功作為SR 度量指標, 討論了噪聲強度對輸出響應和周期力對系統作功的影響, 發現功隨噪聲強度的變化可以呈現雙重SR, 進而從能量的角度, 討論了噪聲誘導的四穩系統雙重SR 機理.
2 四穩勢函數及隨機能量共振
2.1 四穩勢函數及其動力學特性
單位質量的布朗粒子束縛在勢場 V (x) 中, 受到周期力 s (t) 、熱隨機力 Γ (t) 和勢場力 V′(x) 的共同作用, 其動力學方程為

其中, Γ (t) 為強度為 D 、均值為0 的高斯白噪聲,s(t)=Asin(2πft) 表示幅值為 A 、頻率為 f 的周期驅動力, Υ 是單位質量的阻尼系數, 選取合適的單位 Υ =1 , V (x) 為非線性勢函數, 且

式中, a 、b 、c 為勢函數參數, 對 V (x) 求一階導數, 得
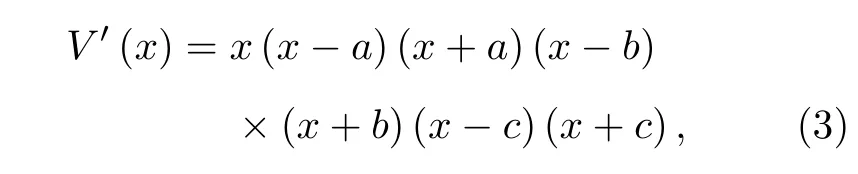
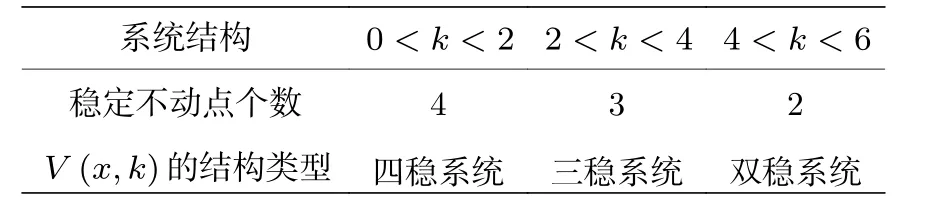
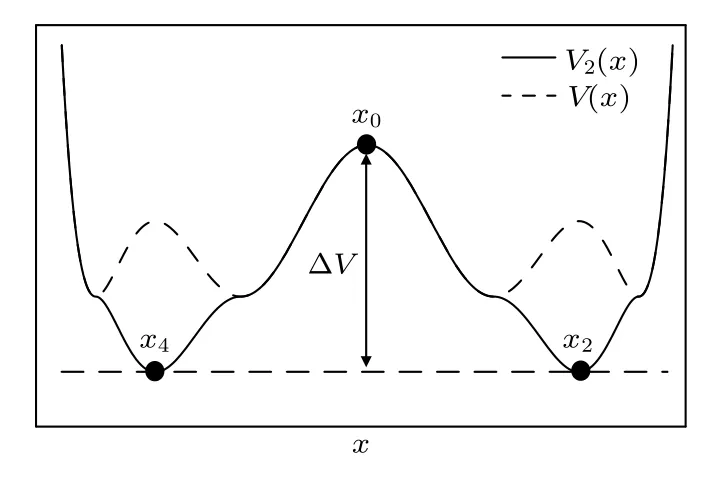
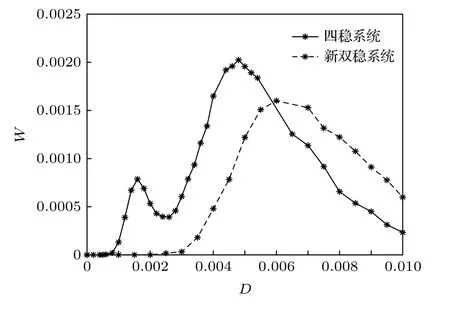
為便于分析, 引入參數 k (0 將其代入(2)式, 得 ?V(x)/?x=0 解方程 , 得勢函數的不動點為 圖1 給出了(5)式的分岔圖, 表明了不動點對參數 k 的依賴性, 實線表示穩定不動點, 虛線表示不穩定不動點.從圖1 可以看出, 當 0 隨著參數 k 的變化, 系統不動點的個數及穩定性隨之而變, V (x,k) 的結構類型與參數 k 的關系總結于表1 中.通過調節參數 k , 可以實現非線性系統在雙穩系統、三穩系統、四穩系統之間切換. 當 0 圖1 非線性系統(5)的分岔圖Fig.1.The bifurcation diagram corresponding to the system(5). 表1 系統結構與參數 k 的關系Table 1.The relationship between potential structure form and parameter k. 圖2 四穩勢函數曲線Fig.2.The potential function curve of the quad-stable system. 其中穩態 x3,6(穩態 x1,5)和左(右)邊勢壘構成小尺度的雙穩系統.左(L)、中(M)、右(R)三個勢壘高度都是 k 的函數 在 k ∈(0,2) 區間內,d(?VL)/dk=d(?VR)/dk >0 , ? VL、 ? VR是單調遞增的; 而 ? VM的變化并非單調, 在區間上單調遞增, 在區間(3?上單調遞減.當時, ? VM、?VL、 ? VR均單調遞增且 ? VM>?VL=?VR, 即中間的勢壘高度大于左、右兩邊的勢壘高度.當四勢阱等深.當中間勢壘高度小于左、右兩邊的勢壘高度.勢壘高度隨參數 k 的變化如圖3 所示. 圖3 勢壘高度 ?V 隨參數k的變化(實線: 左勢壘高度?VL ; 虛線: 中間勢壘高度 ? VM )Fig.3.The relational curve of ? V vs k (solid line: height of the left barrier ? VL ; dotted line: height of the intermediate barrier ? VM ). 四穩系統存在著4 個穩態 x1、 x3、 x5和 x6, 定義 t 時刻粒子從穩態 xi(i=1,3,5,6) 躍遷到xj(j =1,3,5,6) 的概率為, 粒子處于穩態 xi的概率為 pi, 關于 pi的主方程 其中 當周期力幅值 A =0 , 只有隨機力作用時, (8)式的解如下 其中 t 時刻系統輸出為 x 的條件概率 則, 系統輸出的均值〈x(t)〉為 由于 x (t) 是隨機變量, 采用 x (t) 的統計平均〈x(t)〉來刻畫其特性.(14)式表明系統輸出響應〈x(t)〉 依賴于 pi(i=1,3,5,6) , 而(12)式表明pi(i=1,3,5,6) 是由四穩系統參數 k 、噪聲強度 D 等決定的, 所以系統輸出響應 〈 x(t)〉 與四穩系統參數 k 、噪聲強度 D 有關.取信號幅值 A =0.0025 , 頻率f =0.0001 , 四穩系統參數 k =0.8 , 根據(14)式得到不同噪聲強度下系統輸出響應的近似理論曲線,如圖4 所示.圖4 的橫坐標是時間 t , 其單位是秒(s),縱坐標是系統輸出 〈 x(t)〉 , 圖4 表明, 當D =0.0005時, 粒子被束縛在小尺度雙穩系統中做小幅振動.當 D =0.0015 時, 粒子具有的能量變大, 躍過中間勢壘做大幅振動.即, 隨著噪聲強度從0 逐漸增大,粒子由束縛在小尺度雙穩系統中做小幅振動轉變為跨越中間勢壘的大幅振動. (1)式兩邊同乘 d x , 得 圖4 系統輸出響應的近似理論曲線 (a) D =0.0005 ;(b)D =0.0015Fig.4.The approximate theoretical curve of system output response: (a) D =0.0005 ; (b) D =0.0015. U(x,k,t)考慮外力作用下的勢函數 為 求微分得 將(17)式代入(15)式, 得能量平衡方程 其中, 周期力對系統做的元功dW =?2πfAx cos(2πft)dt.平均每個周期外力對系統所作的功為 功 W 與系統輸出響應 〈 x(t)〉 有關, 而 〈 x(t)〉 又是由系統參數 k 、噪聲強度 D 等決定的, 所以功受控于系統參數 k 和噪聲強度 D. 圖5 是 A =0.0025 , f =0.0001 , k =0.8 ,t0=10/f, n =500 時, 功 W 與噪聲強度 D 之間關系的近似理論曲線.與經典雙穩SR 不同, 圖5 所示的曲線呈雙峰形態, 表明四穩系統存在著雙重SR 現象.隨著噪聲強度從0 開始逐漸增大, 粒子先被束縛在小尺度雙穩系統中, 小尺度雙穩系統、周期力和隨機力相互作用產生小尺度SR 現象, 出現第一個共振峰.隨著噪聲強度增大, 粒子在周期力和隨機力協同作用下, 可以躍過中間勢壘做大幅振動,此時四穩系統、周期力和隨機力三者相互作用, 產生大尺度的SR, 出現了更高的共振峰. 圖5 功 W 與噪聲強度 D 之間關系的近似理論曲線Fig.5.The approximate theoretical relational curve ofW vs D. 將兩邊勢壘對稱翻折下來構成新的雙穩勢函數 V2(x) (圖6) 保持 t0=10/f , n =500 不變, 周期力在一個周期內對新雙穩系統作的功 W2為 圖6 勢函數曲線(實線: 新雙穩系統; 虛線: 四穩系統)Fig.6.The potential function curve(solid line: new bistable system; dotted line: quad-stable system). 式中的 r 為克萊默斯逃逸率 粒子躍過勢壘需要的能量與勢壘高度成正比.在新構建的雙穩系統 V2(x) 中, 粒子從左邊勢阱躍遷到右邊勢阱只需要躍過一個勢壘, 其勢壘高度?V 等于四穩系統的中間勢壘高度 ? VM與右(左)邊勢壘高度 ? VR( ? VL)之和.這表明在四穩系統和新雙穩系統中, 粒子從左(右)邊勢阱躍遷到右(左)邊勢阱需要躍過的勢壘的總高度相同.圖7 是保持 A =0.0025 , f =0.0001 , k =0.8 不變, 四穩系統和新雙穩系統的功 W 隨噪聲強度 D 變化的近似理論曲線, 從圖7 可以看出, 周期力對四穩系統、新雙穩系統作的功隨噪聲強度變化的近似理論曲線分別呈現出明顯的雙峰和單峰特性, 四穩系統的兩個共振峰對應的噪聲強度都比新雙穩系統的共振峰對應的噪聲強度小, 說明四穩系統對噪聲較為敏感.同時, 四穩系統的大共振峰對應的功比新雙穩系統的共振峰對應的功更大, 其SR 效應更加強烈,說明小尺度的雙穩SR 增強了大尺度系統的SR 效應. 圖7 功 W 隨噪聲強度 D 變化的近似理論曲線(實線: 四穩系統; 虛線: 新雙穩系統)Fig.7.The approximate theoretical relational curve ofW vs D (solid line: quad-stable system; dotted line: new bistable system). 數值仿真采用四階龍格庫塔算法, 采樣頻率fs=2.5Hz , 粒子初始位置 x (0)=x6, 考慮粒子運動的隨機性, 計算采用500 個周期的均值.圖8 是保 持 A =0.0025 , f =0.0001 , k =0.8 不 變, 功W隨噪聲強度 D 變化的數值仿真曲線, 圖中的實線代表四穩系統, 虛線代表新雙穩系統. 圖8 功 W 隨噪聲強度 D 變化的仿真曲線Fig.8.The relational curve of W vs D. 圖8 表明, 當噪聲強度 D 在 0 ~0.01 區間變化時, 周期力對四穩系統作的功隨噪聲強度的變化曲線呈現“雙峰”特征.隨著噪聲強度從0 開始逐漸增大, 粒子開始在初始穩態 x6附近的單一勢阱內運動, 隨著噪聲強度的增大, 在周期力和隨機力協同作用下, 粒子先在穩態 x3和穩態 x6之間來回躍遷,當噪聲強度為0.0016 時, 功 W 達到第一個極大值0.00079, 對應的輸出信號 x (t) 的時域波形如圖9(a)所示, 時域波形具有非常明顯的周期性特征.隨著噪聲強度從0.0016 繼續增大, 周期力、隨機力與小尺度雙穩系統間的匹配關系逐漸被打破, 周期力的作功能力減弱, 功 W 的數值呈下降趨勢.隨著噪聲強度的進一步變大, 粒子具有的能量增大至能躍過中間勢壘, 在四穩系統的左勢阱和右勢阱之間做大幅振動, 作功能力又開始增強.當噪聲強度為0.0048 時, 大幅振動的頻率與周期力的頻率一致,出現了功的第二個極大值0.0020, 粒子不僅在穩態x1(x3) 和穩態 x5(x6) 之間往復躍遷, 還具有足夠的能量躍過中間勢壘, 做大幅振動, 如圖9(b)所示.噪聲強度從0.0048 繼續增大, 周期力、隨機力與四穩系統之間的匹配度降低, 功 W 的數值呈下降趨勢. 圖9 輸出信號波形 (a) D =0.0016 ; (b)D =0.0048Fig.9.The waveform of the output signal: (a) D =0.0016 ; (b) D =0.0048. 比較周期力對四穩系統、新雙穩系統作的功,新雙穩系統的共振峰對應的噪聲強度為0.0060, 功為0.0016.四穩系統的大共振峰對應的噪聲強度值為0.0048, 功為0.0020, 功的幅度增大了25%.且四穩系統的小共振峰對應的噪聲強度為0.0016, 顯然, 0.0016 < 0.0048 < 0.0060, 表明四穩系統在較小的噪聲強度下就能達到共振. 數值仿真結果表明, 小尺度SR 能顯著提高大尺度系統周期力作的功且四穩系統對噪聲較為敏感.數值仿真結果與理論分析結論基本一致. 本文提出了一類8 次勢函數并討論了其分岔特性, 建立了四穩系統在周期力和隨機力協同作用下輸出響應的近似解析表達式, 引入功這一過程量作為SR 現象的量化指標, 研究了噪聲強度對輸出響應和功的影響.結果表明, 當中間勢壘高度大于左右2 個小尺度雙穩勢的勢壘高度時, 周期力對四穩系統作的功隨噪聲強度的變化曲線呈雙峰形態,四穩系統存在著雙重SR 現象.隨著噪聲強度從0 開始逐漸增大, 粒子先被束縛在小尺度雙穩系統中做小幅振動, 出現第一個共振峰, 隨著噪聲強度繼續增大, 粒子能躍過中間勢壘做大幅振動, 產生大尺度的SR, 出現了更高的共振峰.將四穩系統的左右勢壘對稱翻折下來構成新的雙穩勢函數, 比較周期力對四穩系統、新雙穩系統作的功, 發現小尺度的雙穩SR 增強了大尺度系統的SR 效應且四穩系統對噪聲較為敏感.數值仿真結果與理論分析結論基本一致.本文為今后進一步開展多穩SR 的研究提供了新的思路和方法.
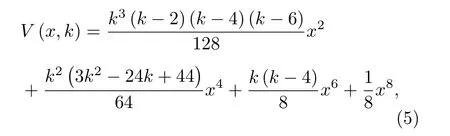



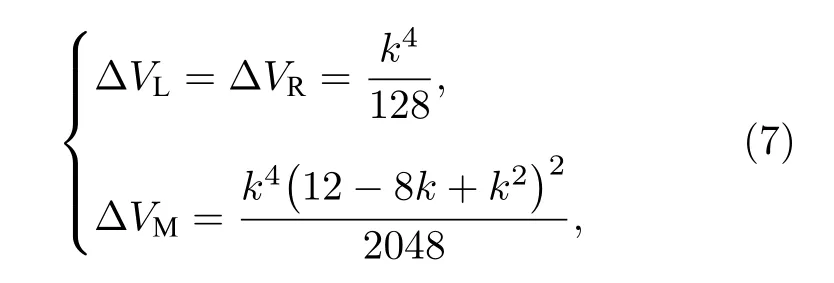

2.2 四穩系統的動態響應

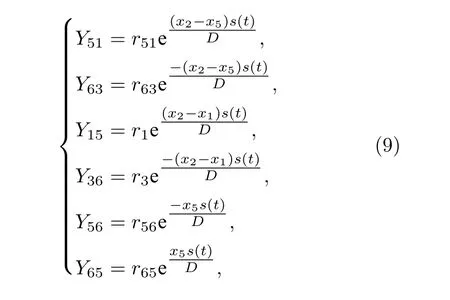

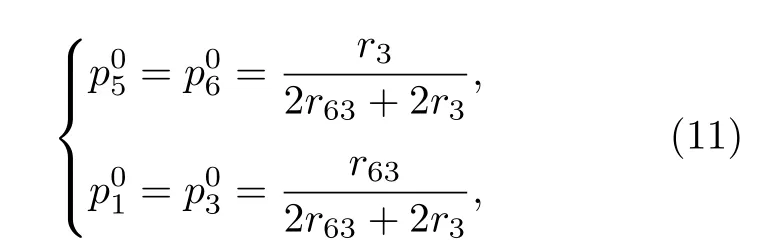


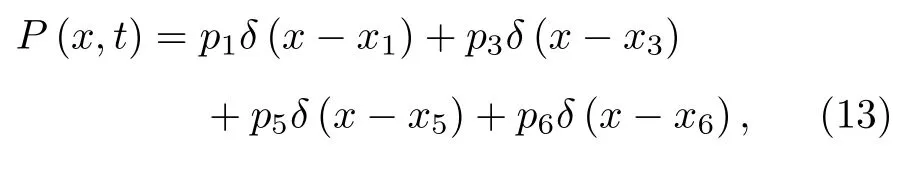
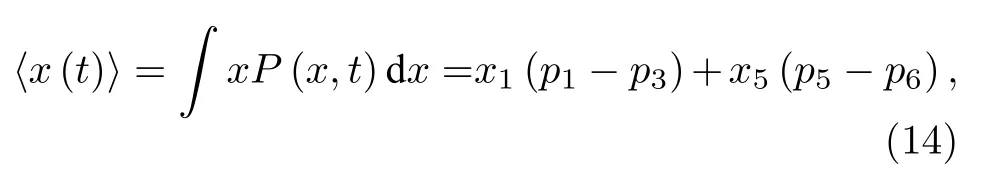
2.3 四穩系統的隨機能量共振
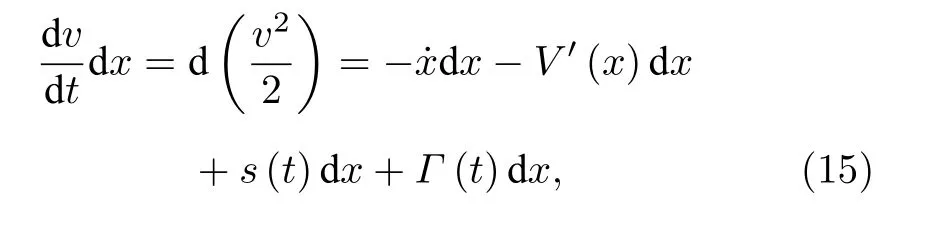

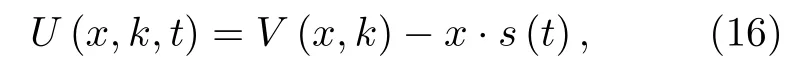
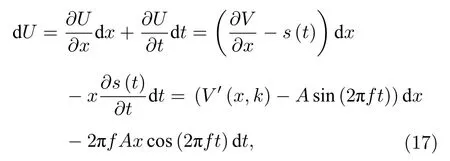
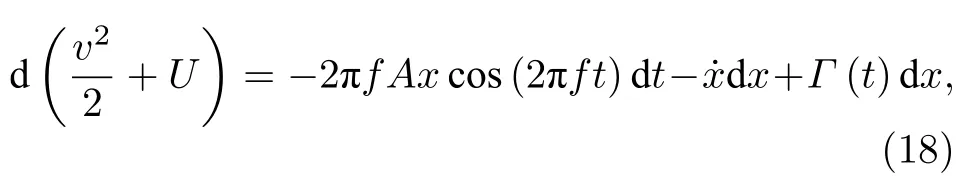
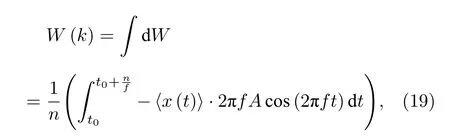

2.4 大小不同尺度之間的共振
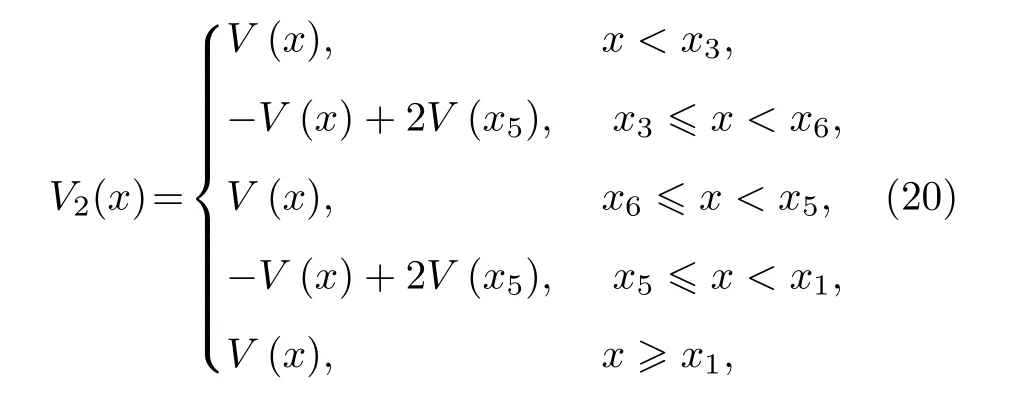

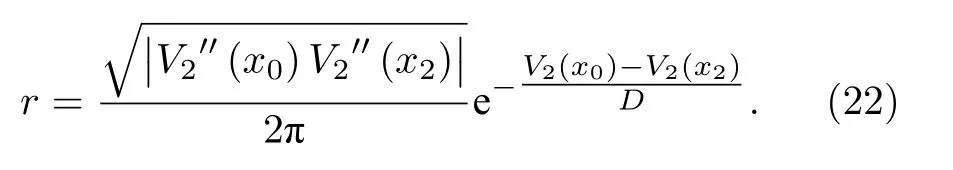

3 數值仿真結果及分析

4 結 論

