基于分子動力學的單晶納米多孔鈦拉伸過程應變率效應和溫度效應研究

劉志強，孟 順，劉宏西，王明強

(江蘇科技大學 機械工程學院，鎮江 212100)

多孔金屬因其較高的表面體積比、良好的力學性能等優點受到了廣泛的關注[1-2].以往的研究主要集中于多孔Au、Cu等FCC晶格金屬，多孔鈦HCP晶格結構拉伸過程中滑移體系的不同和變形機制的復雜而受到了較少的關注[3].分子動力學模擬可實時觀測微觀結構演變過程，通過分子動力學模擬對多孔鈦在拉伸狀況下所展現的力學特性和變形機制研究對于多孔鈦本構規律的發展至關重要，也為多孔鈦在醫學領域人工骨的應用具有很好的推動作用.

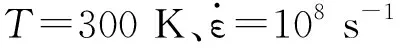
1 多孔鈦建模與模擬方法

1.1 模型構建

基于文獻[10]，多孔鈦模型采用周期性多孔結構生成算法，主要包含4個步驟：① 建立一定大小的空間盒子，在盒子內生成準隨機的種子點，點與點之間的距離控制在相對均勻的范圍內(生成點之前，估算平均分布的時候點與點之間的平均距離，以此為參考確定點之間的最小距離，種子點的添加使用Matlab隨機生成點的命令在模型框架范圍內逐個生成隨機點，每生成一個點都要檢查這個點與其他點的相互距離是否大于要求的最小值，滿足則保留，不滿足則重新生成，直到生成要求的數量，從而保證點與點之間距離不是太遠也不是太近).② 基于生成的種子點云，使用Voronoi tessellation算法[11](基于Voronoi tessellation算法的Voronoi圖由點到線，由線到面，進而由面到體形成多晶框架.空間區域包含n個種子點P，P={P1,P2,...,Pn}，在區域內每兩個相鄰的點連線的垂直平分面進行連接組合，形成一個個多面體，區域中的Voronoi多面體就構成一個整體的Voronoi圖)生成周期性多晶框架，從而保證在X、Y、Z3個方向上能夠實現孔洞結構的周期性分布.③ 在相同的空間盒子內，生成所需取向的單晶鈦模型.④ 以周期性多晶框架的每條邊為中心，以單晶鈦的每個原子為對象進行循環判斷，距多晶框架邊線達到要求距離的保留，未達到距離要求的舍去，最終形成具有周期性單晶鈦孔洞結構.文中構建的盒子大小為30 nm×30 nm×30 nm，種子點數為100個，生成的單晶鈦初始晶格結構為密排六方晶格(HCP)，沿坐標系X、Y、Z軸的取向依次為[1 1 -2 0]、[-1 1 0 0]、[0 0 0 1]，保留原子距最近多晶框架邊線的臨界距離為2 nm，以此條件構建的多孔鈦模型原子總數為1 054 510，孔隙率為28%.多孔鈦模型建立過程及其結果如圖1、2.

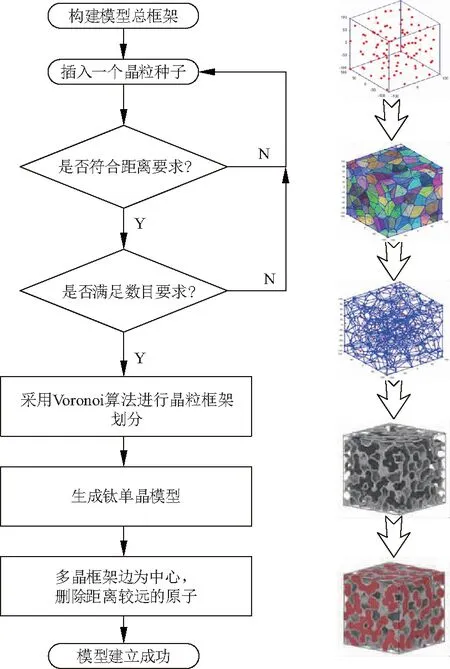
圖1 利用多晶態框架建立單晶納米多孔鈦模型

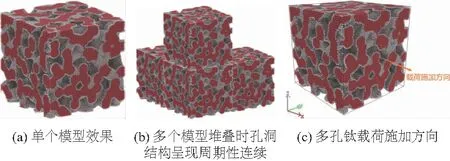
圖2 成型后的具有周期性邊界的多孔鈦模型及其加載方向

1.2 模擬方法

多孔鈦的分子動力學模擬采用美國Sandia國家實驗室開發的開源分子動力學軟件LAMMPS[12].原子間的相互作用勢采用Ti的EAM勢函數[13]為：

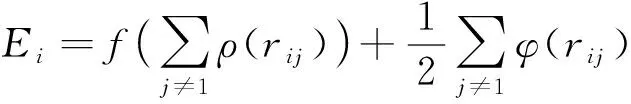
(1)

式中：E為總能量；f為嵌入能量函數；ρ為原子電子密度；φij為對勢相互作用；rij為原子i和j之間的距離.

加載之前，首先對多孔鈦模型進行馳豫，馳豫過程中整個多孔鈦模型在X、Y、Z方向上施加的是周期性邊界條件，先使用共軛梯度法對模型進行能量最小化(共軛梯度能量與溫度和壓強有關，通過命令行執行最小化處理，控制壓強為0，溫度0)，隨后使用Nose-Hoover熱浴法控制體系使多孔鈦模型在等溫等壓系宗下進行相應溫度(100、150、200、250、300、350 K)的恒溫馳豫(NPT馳豫通過命令行執行，控制壓強為0，溫度為指定溫度0.)，弛豫過程中3個體系方向上壓力均保持為0，弛豫時間持續30×10-12s以達到系統能量平衡.馳豫完成后在等溫等壓系宗下沿X軸對模型施加拉伸載荷(圖2(c))，施加載荷時的系統溫度分別控制在相應的馳豫溫度下，即100、150、200、250、300、350 K，每個溫度下施加應變率分別為2×108、4×108、6×108、8×108、109、4×109、8×109、2×1010、4×1010、8×1010s-1的拉伸載荷，整體應變達到20%的時候停止加載，整個過程采用的時間步長為2×10-15s.模擬完成后，使用OVITO basic軟件[14]對模擬結果進行微觀結構演化的可視化分析，不同原子種類的區分和渲染使用的是共同鄰近分析法(common neighbour analysis,CNA)，包括密排六方晶格結構原子(HCP)，面心立方晶格原子(FCC)，體心立方晶格結構原子(BCC)，無定形態原子或邊界原子(OTHER).

2 仿真結果分析

2.1 應力-應變曲線變化規律

通過分子動力學模擬，作多孔鈦在不同應變率和不同溫度下的拉伸應力-應變曲線(圖3).由圖可知，拉伸的初期處于彈性變形階段，應力隨應變呈線性增加的趨勢.應變的繼續增大，曲線過屈服點后，多孔鈦轉變為塑性變形階段，應力增加趨勢減緩，并達到最高點的強度極限.值得注意的是，相同溫度下，當應變率小于109s-1，不同應變率對應的最大強度極限隨應變率增加而增加，但是不明顯；當應變率大于109s-1時，隨著應變率的增加，最大強度極限的增加趨勢更加明顯.說明多孔鈦材料具有不同的應變率敏感性，更高的應變率下具有更大的抗拉強度.這與單晶鈦納米線和多晶鈦在不同應變率下拉伸所得規律一致[8-9].

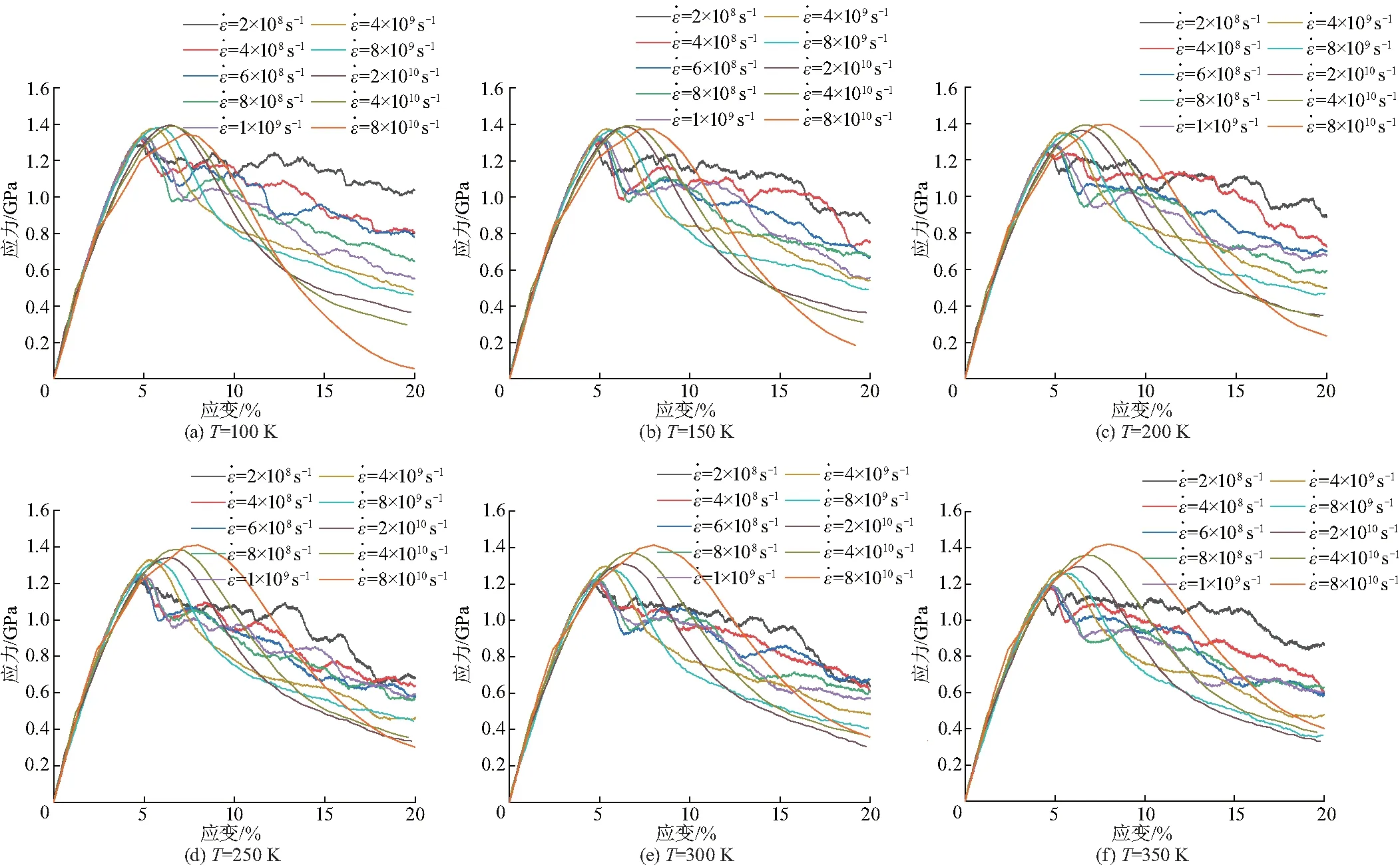
圖3 多孔鈦在不同溫度和應變率作用下的應力-應變曲線

進一步研究不同溫度下，材料最大強度極限隨應變率的變化趨勢(見圖4).由圖可知，當溫度相同時，多孔鈦最大強度極限總體趨勢隨應變率的增大而增大；當應變率相同時，隨著溫度的增加，最大強度極限呈現減小的趨勢.此外，溫度相對較高的多孔鈦模型在拉伸過程中，最大強度極限變化的曲線更加的陡峭，說明溫度對多孔鈦模型力學特性具有一定的影響.

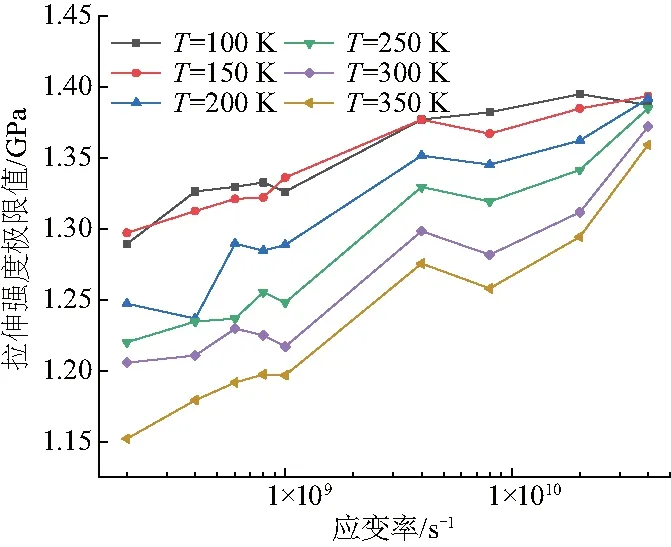
圖4 不同溫度下多孔鈦材料拉伸強度

為了更好地分析多孔鈦這一特點，采用線性擬合應變率(對數)-最大強度極限，得到多孔鈦模型的應變率敏感性[15-16]隨溫度變化的趨勢(圖5).由圖可見，隨著溫度的增加，多孔鈦材料的應變率敏感性逐漸增大.同一應變率下，更高溫度導致更低的最大強度極限.此外，通過觀察多孔鈦拉伸的應力-應變曲線(圖3)發現，在經過屈服點后，其呈現彎曲狀態且上下波動，這在通過最大強度極限下降過程中尤為明顯，這是由于在拉伸過程中所產生的各種變形機制的相互作用引起的.

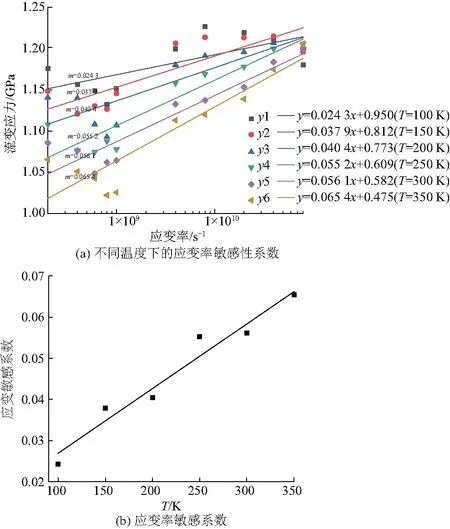
圖5 不同溫度下多孔鈦材料的應變率敏感性

2.2 不同應變率和不同溫度下多孔鈦微觀變形機制

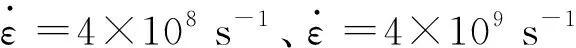
圖6 不同應變率下的拉伸變形過程

分析多孔鈦材料模型在拉伸應變0～20%下的總體變化過程.當拉伸應變為4%時，材料處于彈性變形階段，微觀結構無明顯變化，內部為HCP晶格結構原子；當拉伸應變達8%左右時，材料處于塑性變形階段，通過觀察微觀變形可以發現，模型出現了由邊界原子發射的肖克萊不全位錯所產生的孿晶[17]和堆垛層錯(圖7)，此外還發生了相變(HCP晶格結構轉為BCC晶格結構)；拉伸應變的繼續增大，更多的位錯(孿晶和堆積斷層)被激活和更多的相變產生.

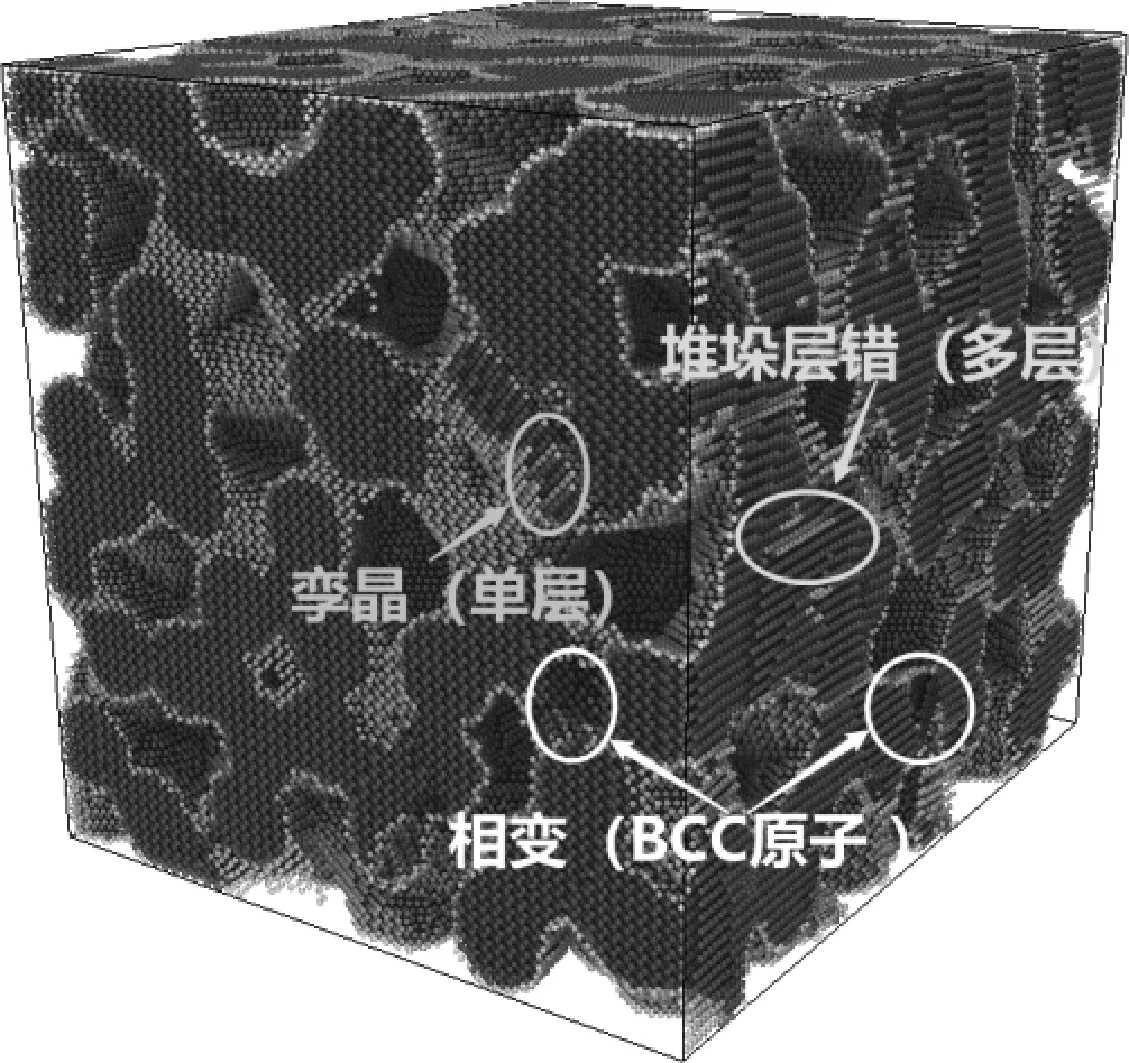
圖7 拉伸過程中的位錯和相變情況

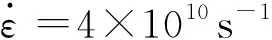
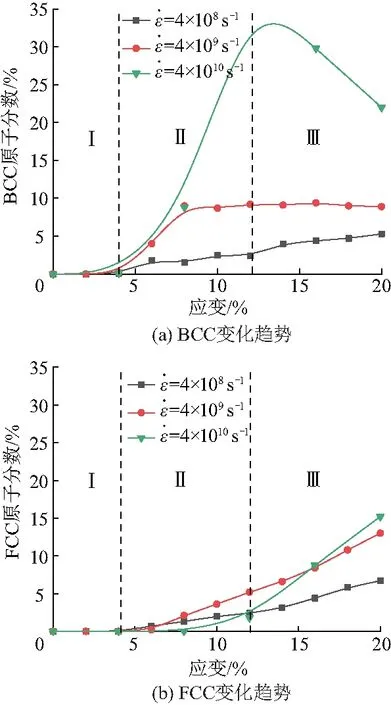
圖8 不同應變率下各個原子數量隨應變的變化趨勢

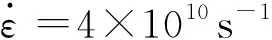
圖9 不同應變率下位錯密度分布

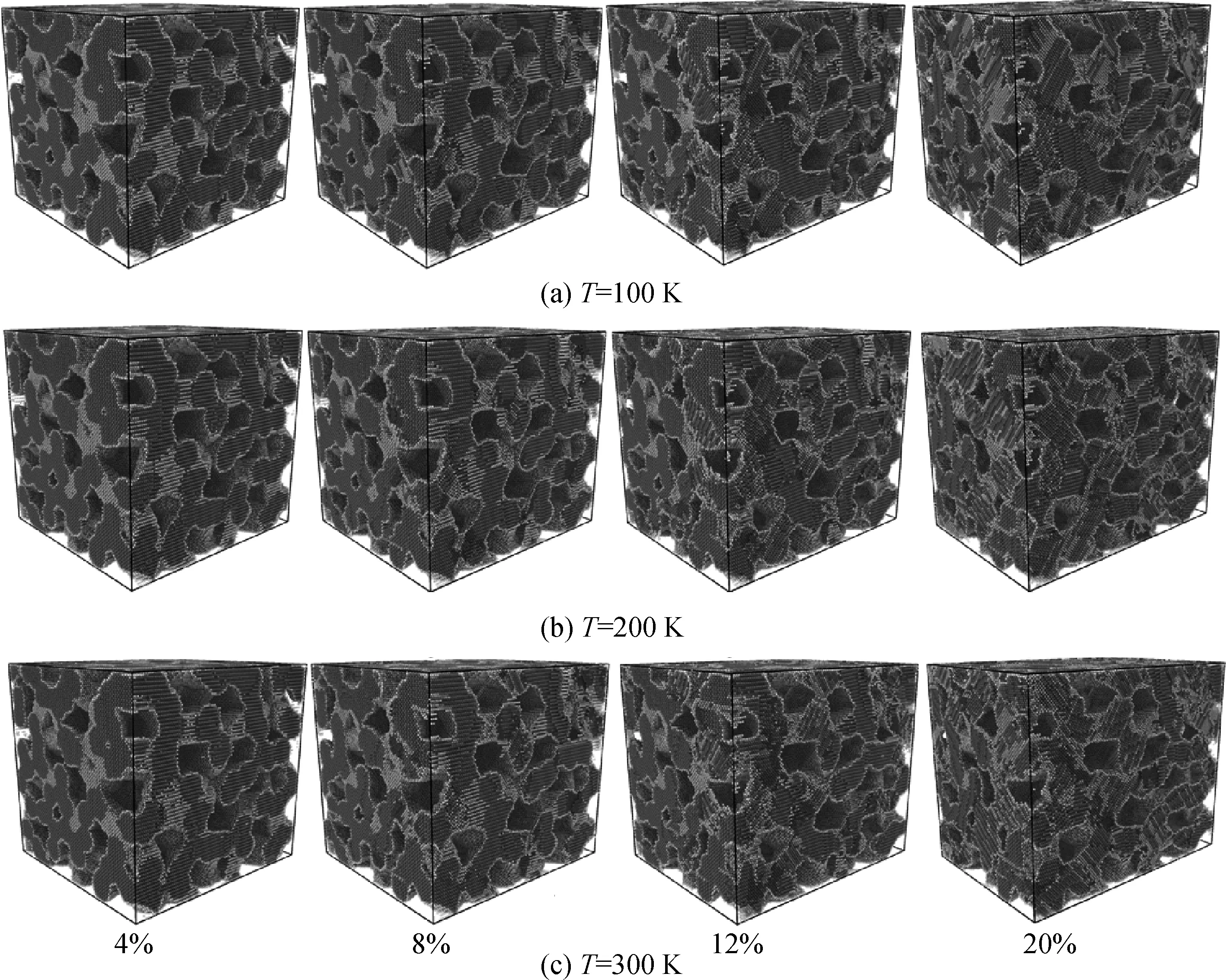
圖10 不同溫度下的多孔鈦拉伸微觀變形過程

表1 多孔鈦拉伸過程BCC數量統計

在拉伸變形過程中，與不同應變率下相變明顯變化情況所不同的是，不同溫度產生的相變比例基本一致.這說明影響相變變化的主要因素為應變率.由圖11可知，不同溫度下的FCC晶格原子數量也基本一致，即不同溫度下的位錯運動也基本一致.由此表明，導致多孔鈦拉伸強度極限降低另有原因.

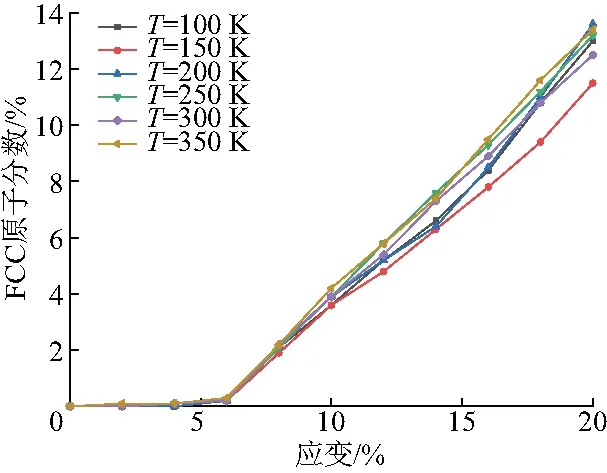
圖11 不同溫度下FCC隨應變的變化趨勢

進一步分析不同溫度對白色邊界原子的影響(圖12)，不同溫度下多孔鈦邊界白色邊界原子數量隨應變的變化趨勢，并針對每個階段變化情況分析其微觀變形情況(圖13).白色邊界原子變化主要分為3個階段.第Ⅰ階段(0～4%)，拉伸處于彈性變形階段，邊界白色邊界原子數量變化不明顯；第Ⅱ階段(4%～12%)，此時白色邊界原子急劇上升，這是因為隨著能量的增加及外界的載荷的作用，更多的HCP原子劇烈運動偏離原來穩定的位置，從而被識別為邊界白色邊界原子.如圖13圓圈標記A到B、C，白色邊界原子明顯增加；第Ⅲ階段(>12%)，白色邊界原子數量增加趨勢減緩，如圖12中圓圈標記D到E變化，白色邊界原子數量增加減緩，此階段下主要的微觀變形機制為位錯運動.

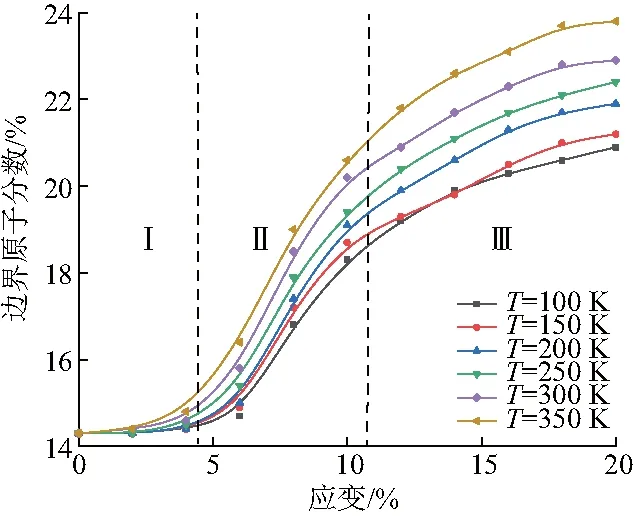
圖12 不同溫度下多孔鈦邊界白色邊界原子

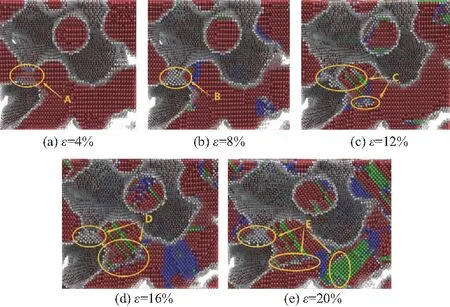
圖13 不同階段邊界白色邊界原子生長情況

在同一應變下，溫度越高，能量越高，原子運動越劇烈，導致更多的原子運動偏離穩定位置，被識別為白色邊界原子，如圖14圓圈標記F、G、H，白色邊界原子數量隨溫度升高而增大.這表明高溫促進了白色邊界原子的生長.不同于相變和位錯的微小變化，高溫度下邊界原子的運動與生長更劇烈，邊界運動變化為最主要的變化，從而導致材料更容易產生塑性失效，材料的最大抗拉強度極限減弱.

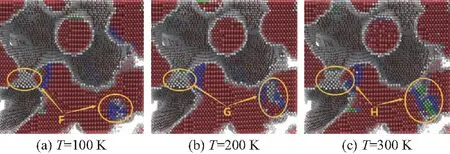
圖14 不同溫度下應變相同(8%)的同一

3 結論

基于分子動力學模擬分析了多孔鈦材料在不同應變率和不同溫度下的拉伸力學性能及變化規律，得到以下結論：

(1) 多孔鈦具有應變率強化和溫度軟化的特點.

(2) 多孔鈦材料在拉伸變形初期主要發生相變、位錯運動和邊界生長，在拉伸后期的主導變形機制為位錯運動.

(3) 不全位錯的滑移為最主要的位錯運動方式.

(4) 高應變率抑制了位錯運動的產生，更多HCP晶格結構相變為BCC晶格結構，從而使得材料的最大抗拉強度極限明顯增強.

(5) 影響相變變化的主要因素為應變率.

(6) 溫度升高時相變和位錯的變化相差無幾，邊界運動生長劇烈導致材料的最大抗拉強度極限降低，材料出現軟化現象.