跨座式單軌弓網耦合主動控制研究
劉朝濤,狄科宏,杜子學,楊 震
(重慶交通大學 機電與車輛工程學院,重慶 400074)
0 引 言
跨座式單軌交通作為城市軌道交通的一個重要分支,具有爬坡能力強,轉彎半徑小等優點,已成為重慶市公共交通不可或缺的一部分[1]。跨座式單軌的接觸網為剛性接觸網,且橫向安裝在軌道梁的側壁,其弓網關系為剛體與剛體之間的耦合關系,而剛性接觸網的不平順會產生許多接觸硬點。列車通過這些硬點時,受電弓的相對位置與速度會發生瞬態變化,尤其在高速通過時,受電弓會頻繁地撞擊接觸網,一是會造成較大的運行噪聲;二是會加大接觸力的波動從而加劇弓頭與接觸網的機械磨損,且長期運行會造成受電弓的斷裂影響行車穩定性與安全,不僅降低了其使用壽命,也提高了運行維護成本;三是列車通過接觸網硬點時產生的短暫脫弓離線會出現拉弧現象,由此帶來的電氣磨損不僅會灼傷弓頭,同時也會破壞列車電氣穩定性從而造成電氣元件的損壞。因此,對于受電弓主動控制研究具有很大的意義,同時也是軌道交通電氣化發展不可或缺的一部分。
主動控制是基于現代控制理論,在不影響受電弓內部結構參數前提下,使用相關自動化技術對其施加外力來降低弓網接觸力波動[2]。目前國內外對于受電弓主動控制的研究均是針對鐵路系統的受電弓,而對單軌受電弓主動控制的研究少之甚少。跨座式單軌受電弓相比于其他制式的受電弓設計較為獨特。受電弓的底座與框架間安裝存在升弓彈簧。該彈簧主要作用是在單軌列車行進過程中為弓網間的接觸提供自適應力。而在列車高速行進過程中,升弓彈簧的響應速度非常有限,若受電弓在通過第一個接觸網硬點而發生了位移變化,在通過第二個硬點之前沒有完成調節,則受電弓與接觸網之間極有可能會發生碰撞。因此,需要加入執行機構來進行主動干預與快速調節。筆者所研究的主動控制是以無刷直流電機為執行機構。為了不改變受電弓內部結構參數,筆者將電機與框架連桿直連,考慮到電機的啟動以及動態性能,選擇雙閉環控制器。為了兼備控制精度與控制速度,選擇分數階PID作為系統的控制器。系統整體結構如圖1。

圖1 系統結構
1 弓網耦合模型
單軌受電弓在結構上與其他受電弓有較大差異,但在工作模式以及動態特性上具有很大的相似性。因此在進行受電弓動力學分析的時候,可參考現有的方法進行分析。考慮到弓網耦合工作在平衡位置時,弓網接觸點的動態波動范圍不大,因此,可以對受電弓的動力學模型進行線性化處理。
將受電弓框架部分以及弓頭部分看作單獨的質量塊,它們之間以等效的剛度和阻尼相連,便得到了受電弓的二質量歸算模型[3]。
跨座式軌道交通接觸網的布置形式不同于其他軌道交通的接觸網。通過錨段關節連接每一段伸縮單元并固定在軌道梁的側壁,受電弓則橫向安裝在軌道列車的底部裙板。單軌列車的弓網耦合系統為橫向接觸受流,因此可以忽略重力以及空氣阻力的影響。
理論上跨座式單軌交通的剛性接觸網不存在彈性,但在弓網耦合過程中,接觸網在振動的影響下會產生一定的彈性變形,因此筆者在建模時考慮了接觸網的彈性特性。同時,考慮到接觸網的特殊結構形式,為了方便建模,將支持絕緣子視為剛體。而匯流排與接觸線在夾緊力的作用下具有近似相同的動力學特性,可將其視為整體。因此得到的弓網耦合模型如圖2。

圖2 弓網耦合模型
系統的運動微分方程:
(1)
k2(zr-z2)+F0
(2)
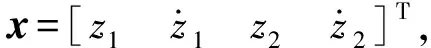
(3)
式中:
C=[ks0 0 0]
其中:q與w(t)分別為剛性接觸網不平順與車身振動引起的激勵;F0為靜態抬升力。
2 三相無刷直流電機的雙閉環模型
永磁無刷直流電機相比于傳統的直流電機,具有維護成本低、機械效率高、功率密度高、易于控制等優點,已廣泛應用于各種工業工程場合[4]。其常用的控制方法有電壓直接控制以及電流、轉速雙閉環控制等。電壓直接控制會產生較大的轉矩脈動,降低電機運行可靠性,無法應用于高性能要求的場合。而雙閉環控制解決了電壓控制轉矩脈動大的缺點,且具有啟動速度快、動態性能好等優點[5]。因此選擇雙閉環的無刷直流電機控制策略。
2.1 無刷直流電機數學模型
三相星形繞組的無刷支流電機滿足條件:
il1+il2+il3=0
(4)
且有:
Mil1+Mil2+Mil3=0
(5)
則定子的電壓平衡方程:
(6)
式中:M為相鄰兩相繞組互感;L為每相的自感。
電機的電磁轉矩由永磁轉子磁場與定子繞組電流相互作用產生,其數值為通過每相的電磁功率與轉子轉速之比,表達式如式(7):
(7)
則轉子的運動方程為:
(8)
式中:Ω為轉子角速度;B為阻尼系數。
2.2 逆變器模型
逆變器為MOSEFT管六臂全橋驅動模型,導通方式為二二導通,不考慮電容保護電路的影響,且假設開關管與二極管具有理想的開關特性。逆變器拓撲如圖3。
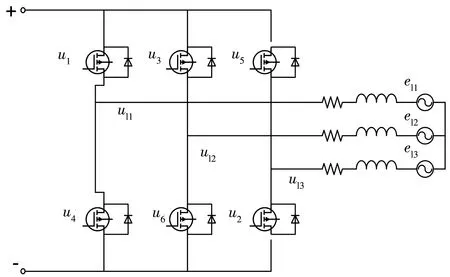
圖3 逆變器拓撲
在某一時刻,l1、l2相導通,此時il3=0。根據三相繞組的電壓平衡方程,可得:
(9)
聯立可得中點的電壓為:
(10)
在換相臨界位置,l3相導通,il3>0,并產生反向的感應電動勢,此時的電壓平衡方程為:
(11)
此時的中點電壓為:
(12)
式中:Udc為直流側電壓。通過判斷下一時刻換相相的電流可求解不同換相時刻的中點電壓,結合感應電動勢進而可求得逆變器輸出至三相繞組的端電壓。
2.3 電流滯環控制模型
電流滯環控制的作用主要是對三相繞組的電流進行跟蹤并調節,對繞組起到一定的保護作用,其次是根據電機霍爾傳感器的信號以及電流的誤差信號輸出相應的PWM信號。
當電流的正向誤差大于滯環比較器的環寬時,輸出對應相正向導通,負向關斷的PWM信號;當電流的反向誤差低于環寬的邊界,輸出對應相反向導通、正向關斷的PWM信號。因此,電流的調節在滯環環寬內呈鋸齒狀波動。
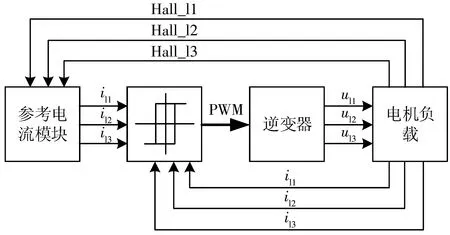
圖4 電流滯環控制
2.4 轉速環控制模型
轉速環換采用PI控制,通過轉速誤差輸出不同的參考電流,實現轉速的快速調節以及穩態無靜差,同時對負載變化引起的干擾起到一定的抵抗作用。為防止電流過大,需要在參考電流輸出位置加入限幅模塊[6]。
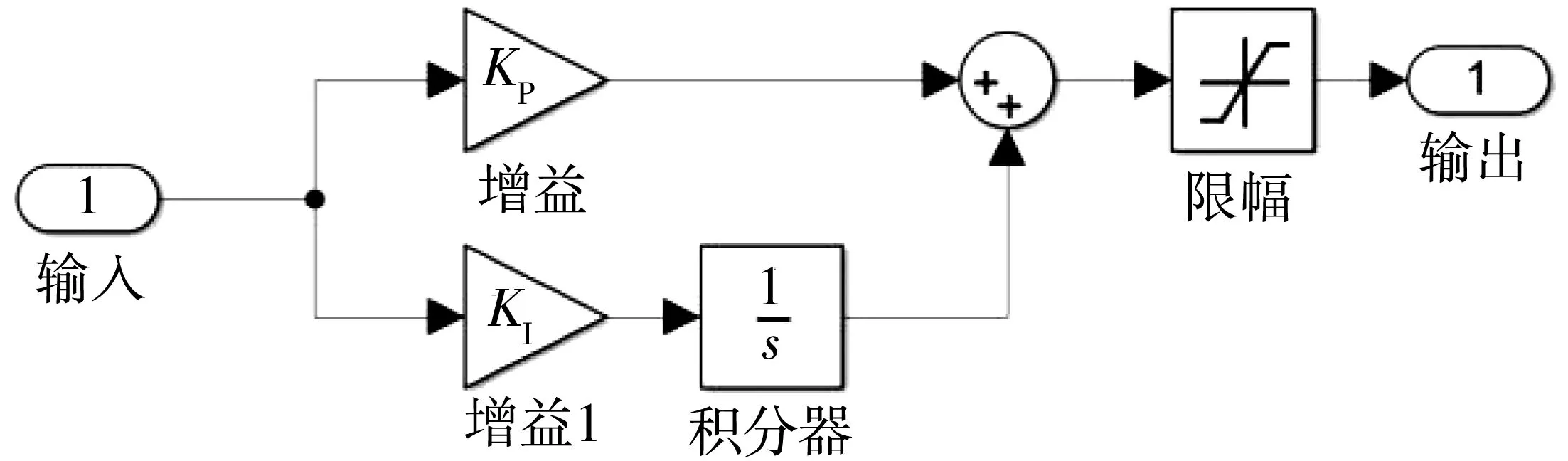
圖5 轉速換PI控制
3 分數階PID控制器設計
3.1 分數階PID模型
分數階PIλDμ是PID在整數階微積分的擴展,引入了λ與μ的微積分階次參數,使得控制系統的調節范圍更廣,且具有靈活性。相比整數階PID,其對系統內部的多變量以及非線性因素具有更強的調節特性。因此,分數階PID控制器具有更好的動態性能及魯棒性[7]。
分數階微積分常用的基本函數有Gamma函數、Beta函數和Mittag-Leffler函數,其中Gamma函數定義如式(13):

(13)
Gamma函數滿足式(14):
Γ(x+1)=xΓ(x)
(14)
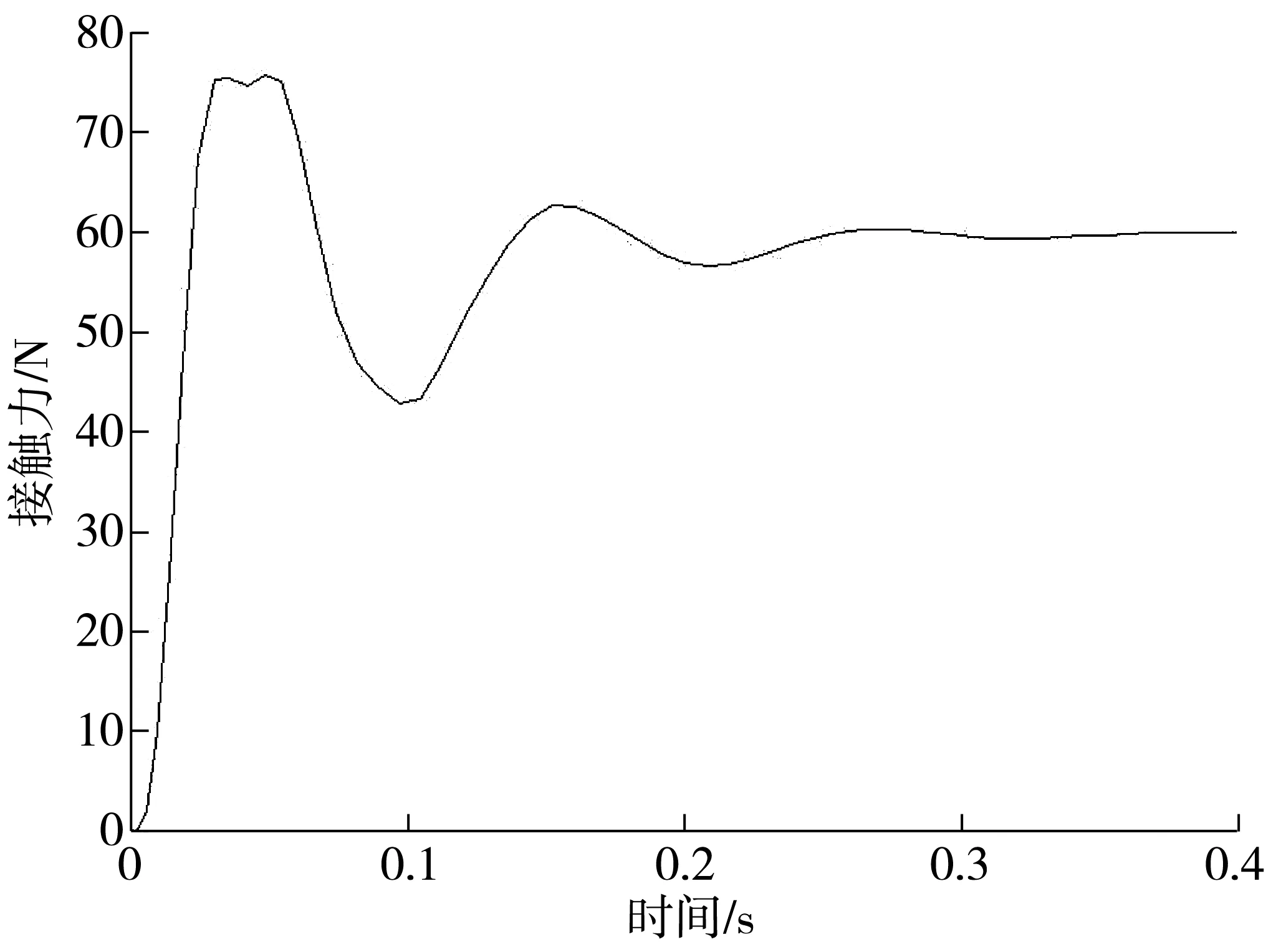
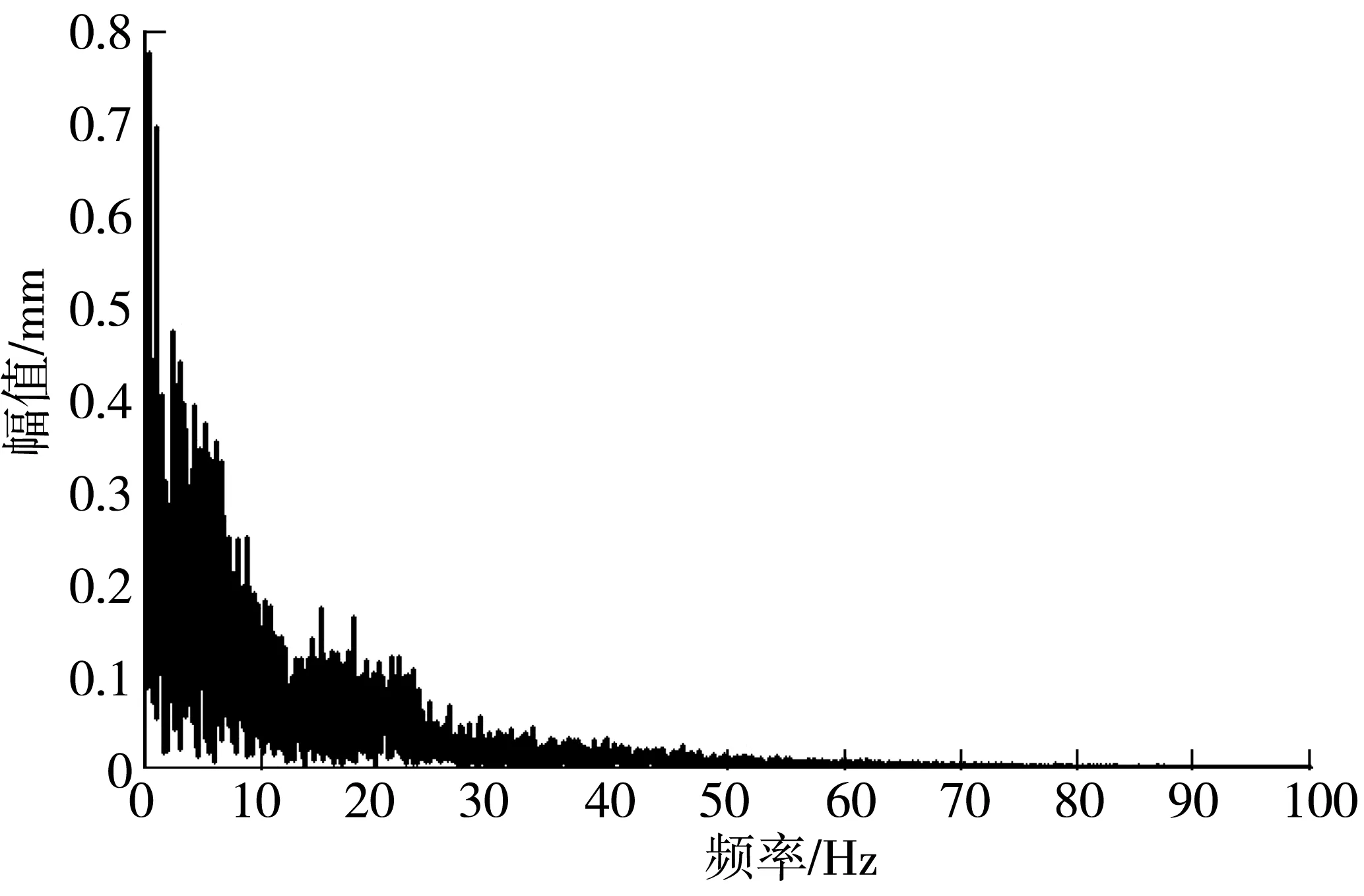
分數階微積分的定義在整數階微積分定義基礎上推廣與歸納而來,是整數階的一般形式[8]。目前分數階微積分的定義有3種,分別為Grunwald-Letnikov(GL)定義、Riemann-Liouvile(RL)以及Caputo定義。其中RL是建立在Gamma函數基礎上,對于任意實數p,滿足m-1 (15) 積分形式為: (16) 拉普拉斯變換同樣可以用來描述分數階控制系統。分數階PID的傳遞函數可以描述為: (17) 積分環節能夠提高系統的型別,進而增加系統的穩定性。對于整數階PID,一階積分環節會帶來系統的90°相位遲滯,從而影響系統的動態性能。通過調節積分階數λ,使得系統的相位滯角在0~180°變化,可以同時兼顧系統的動態性能以及穩定性。微分環節會產生一個超前的90°相角,從而做出誤差的提前修正,增加系統的阻尼特性,提高系統的動態性能。同理,通過調節微分階次μ,使得超前相角在0~180°變化,使得系統阻尼的調節范圍更大,從而達到系統的性能要求[9]。 通常計算分數階系統具有一定的難度,需要將分數階次近似為整數階,再利用整數階的計算方法進行求解,提高計算效率。目前分數階近似有兩種途徑,一種是間接近似,另一種是直接近似。直接近似法是將分數階系統離散化,然后進行求解;間接近似需要在頻域內選定合適的頻域范圍,再通過算法對分數階進行整定。目前最常用的近似算法為Oustaloup法,該算法通過設計Oustaloup濾波器對輸入的分數階系統進行近似化。假設近似對象[10]: R(s)=sα (18) 選定擬合頻段(ωb,ωh)以及近似階次N,則濾波器的輸出高階傳遞函數為: (19) 其中增益以及零極點為: (20) 頻段的選取標準應能盡量提高精度,但是精度的提高將伴隨著計算速度的下降。對于近似的階次,理論上階次越高,近似效果越好,但是當擬合階次達到某一值時,逼近精度將不再有明顯的提高。因此,在選取擬合頻段以及階次時應綜合考慮系統性能和精度的要求。 對于弓網系統,靜態抬升力F0=100 N。升弓彈簧以及弓頭支座的橡膠彈簧剛度和阻尼系數參數通過儀器實驗測得,分別為k2=12 900 N/m、c2=100 N·s/m、k1=17 000 N/m、c1=200 N·s/m。弓頭以及框架的等效質量m1=2.49 kg、m2=10.54 kg。接觸剛度ks=8 700 N/m。剛性接觸網的支持絕緣子間距L=2 m[11]。激勵均看作白噪聲,功率設置為10-7。 電機采用雙閉環控制,其參數如下:轉動慣量J=0.001 56 kg·m2;定子繞組電阻R=4.526 Ω;電感L=0.002 H;阻尼系數B=0.0002 N·m·s/rad;極對數p=2;電源為直流220 V;電流限幅為±30 A;轉速環KP=20;KI=0.15;采樣周期T=0.000 1 s;積分階次為0.9;微分階次為0;控制器的KP=0.08;KI=0.01;近似階次N=4。 評價弓網受流質量的主要指標有平均接觸力、最大接觸力、最小接觸力、接觸力標準差以及離線率[12]。對于跨座式單軌交通,規定弓網接觸力的最佳值應在59±10 N之間,而接觸力在44~79 N之間便可保證弓網之間的正常受流。 單軌列車安裝有多個受電弓,且均勻分布在列車兩側,只取一側單個受電弓進行分析。受制于跨座式單軌交通特殊的承載方式,列車直線段行駛的最高時速不能超過80 km/h[13]。因此,讓列車以60、80 km/h 兩種不同速度在直線段勻速行駛,通過對比不同時速下被動與主動控制的接觸力響應來分析主動控制對弓網接觸力的影響。 圖6為直線段不同時速下接觸力的時域響應曲線。由圖6和表1可知,直線段60、80 km/h時速下弓網離線率均為0;在速度為60 km/h時,控制效果明顯,接觸力基本穩定在54~68 N之間,接觸力的波動明顯降低,弓網處于最佳受流狀態;而速度為80 km/h時,控制效果相比低速狀態要減弱一些,但接觸力大部分時間均能穩定在47~72 N之間,能夠完成弓網間的正常受流。 圖6 直線段不同時速下接觸力響應曲線 表1 不同時速下弓網受流質量評價指標統計 圖7為直線段不同時速下弓頭位移曲線。同理,在速度為60 km/h時,主動控制能明顯改善弓頭的振動,而在速度為80 km/h時,控制效果隨著速度的增加而變弱,原因是隨著車速的增加,弓網對于高頻信號也愈發敏感,而電機的響應速度為一定值。 圖7 直線段不同時速下弓頭位移曲線 表2 不同時速下弓頭位移評價統計 圖8為階躍輸入下電機主動控制的接觸力響應曲線,接觸力在從0~60 N的上升時間為0.02 s左右。圖9為實測截取的重慶軌道交通3號線雙龍至碧津直線段70 km/h的弓頭位移頻響特性曲線。引起弓頭振動的頻率主要集中在0~30 Hz以內,主動控制的反應速度能夠應對該頻段內的激勵信號。因此,電機主動控制的模型雖然對于高速弓網的調節有些欠缺,但對于跨座式單軌列車,其調節效果能夠滿足弓網的正常受流。 圖8 階躍輸入接觸力響應 圖9 直線段70 km/h弓頭位移頻響特性 建立了線性二自由度弓網耦合質量歸算模型,以及無刷直流電機的雙閉環控制模型,利用分數階PID控制器模擬并分析了弓網接觸力的響應,實驗結果表明: 1)在直線段60 km/h下,主動控制的接觸力標準差相比被動控制減少了43.3%,弓頭位移的標準差相比被動控制減小了35.8%,且接觸力基本維持在49~69 N的最佳弓網受流區間;而在80 km/h下,主動控制的接觸力標準差相比被動控制減少了30.0%,弓頭位移的標準差相比被動控制減小了30.7%,接觸力基本維持在44~79 N的正常受流區間,證明所設計的主動控制系統能有效降低接觸力波動,改善弓頭振動,提高受流質量。 2)在響應速度方面,主動控制的響應時間在0.02 s左右,而根據實測數據,引起弓網振動的頻段主要集中在0~30 Hz以內,因此控制系統能夠進行快速響應與有效調節,進一步驗證了所設計主動控制系統的有效性。3.2 分數階次的近似
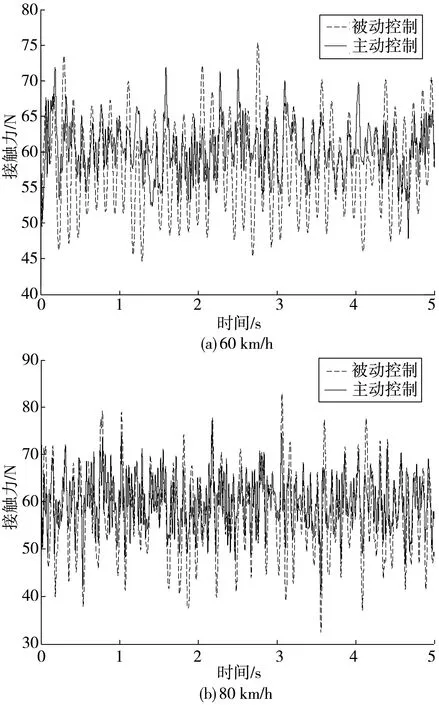
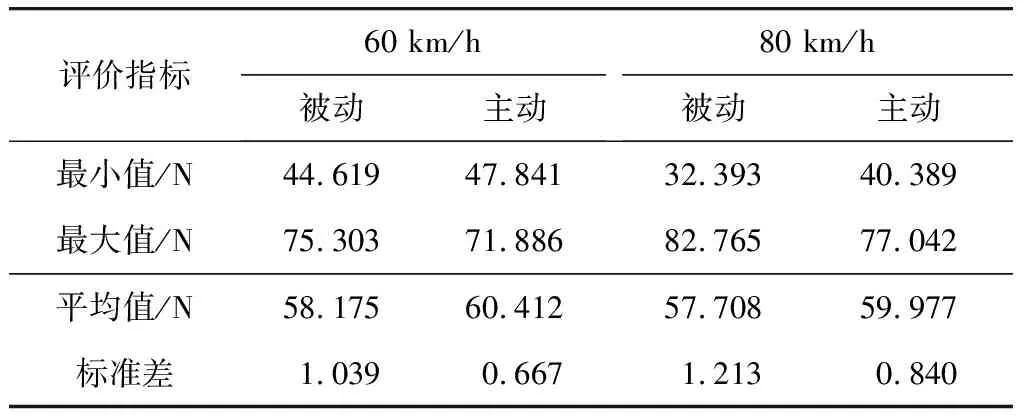
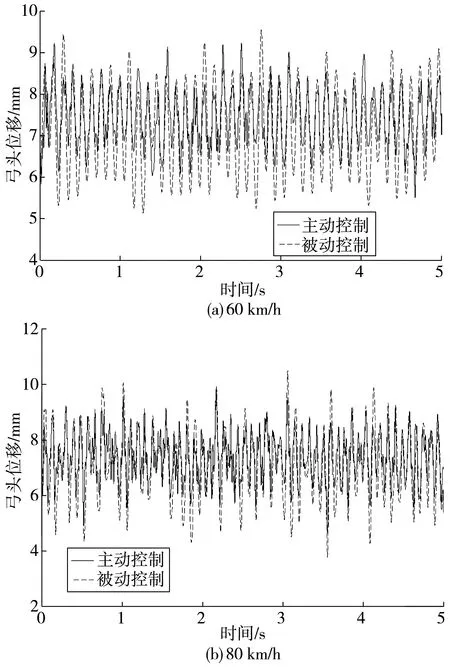
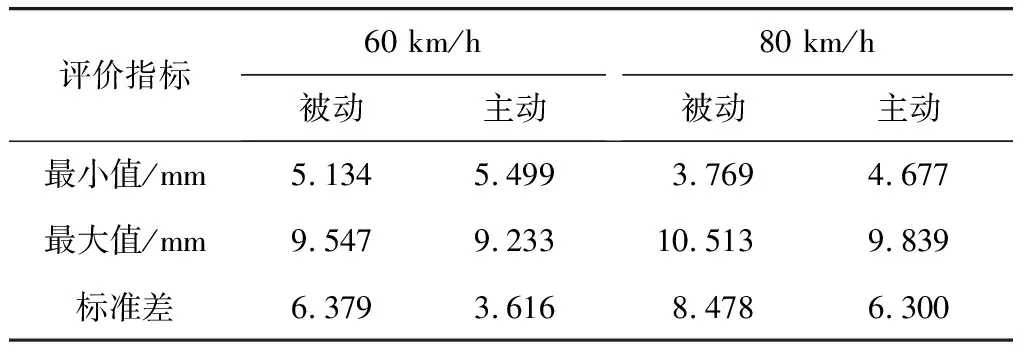
4 仿真實驗分析
4.1 系統參數設置
4.2 接觸力與弓頭位移響應分析
5 結 論

