反應密度泛函理論的構建與初步應用

唐偉強，謝鵬，徐小飛，趙雙良，

（1 華東理工大學化學工程聯合國家重點實驗室，上海200237； 2 廣西大學化學化工學院，廣西石化資源加工及過程強化技術重點實驗室，廣西南寧530004）

引 言

能源、資源和環境是人類社會賴以生存和發展的基礎。隨著人口的增加和社會的發展，人類消耗的能源和資源急劇增加。能源利用效率低、資源浪費嚴重、生產過程不夠清潔，不僅引起一些資源和化石能源的快速枯竭，污染物的排放也快速增長，環境污染加重，大量的溫室氣體排放更是引起全球氣候變化、極端災害性天氣頻發，成為全球政治的焦點。在這樣的大形勢下，發展綠色化工、提高過程效率，降低能耗和污染具有重要的社會意義和經濟價值。

根據“綠色化學十二原則”，綠色化工的理念體現在反應路徑高效環保、能耗低、反應速率快、反應轉化率和選擇性高[1]。大多數化學反應都是在溶劑中發生的，溶劑能較大程度上調控化學反應的效率。例如，Han 等[2]發現以超臨界CO2為溶劑可使苯酚加氫制備環己酮反應的產率和反應速率大大提高，解決了傳統反應路線選擇性差、效率低這一挑戰性難題。最近，Kong 等[3]發現溶劑效應對脫羧/羧基化反應的實現是至關重要的。此外，如圖1所示，實驗發現混合溶劑的組成及其配比對化學反應有著顯著的影響[4?5]。選擇合適的反應溶劑已成為反應工程中調控化學反應選擇性和轉化率的控制步驟。

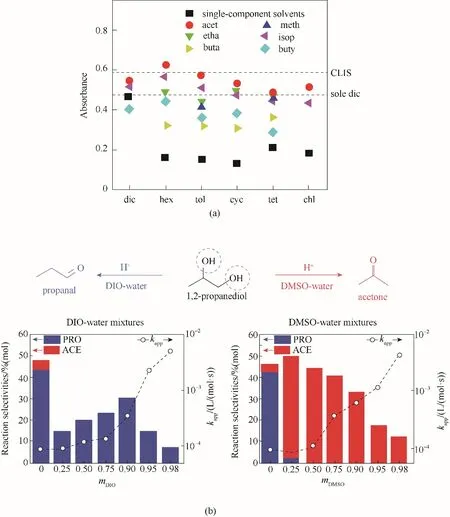
圖1 混合溶劑對化學反應的影響：（a）量子點在TiO2膜上的吸附量嚴重依賴分散的溶劑[4]；（b）1,2?丙二醇在1,4?二氧六環（DIO）水溶液中脫水生成丙醛，在二甲基亞砜（DMSO）水溶液中生成丙酮，反應速率在不同混合比例下相差較大[5]Fig.1 The effect of mixed solvents on chemical reactions:(a)The absorbance of quantum dots adsorbed on the TiO2 film is heavily dependent on the dispersed solvent[4];(b)1,2?propanediol was dehydrated in 1,4?dioxane(DIO)aqueous solution to form propanal and in dimethyl sulfoxide(DMSO)aqueous solution to form acetone,and the reaction rates differed greatly under different mixed solvent ratios[5]

溶劑特性（包括種類、結構和流動特征等）對反應的影響可從兩個角度來剖析。從反應自由能來看，反應自由能分布受到溶劑的分子作用力影響。當溶質（反應物或產物）在溶劑中溶解時，溶劑和溶質之間產生分子作用力[6]。這些作用力的存在使得反應物分子在反應過程中改變原來的結構而轉化為另外一種物質時，必然受到溶劑和其他溶質的影響。溶劑特性、溶劑的微觀結構等強烈地影響反應物和過渡態的穩定性，從而影響反應過程和反應速度，影響反應的活化能[6?8]。同一反應使用不同的溶劑，反應效果相差甚大[9]。這是因為不同溶劑中反應體系微環境不同。在化學反應工程中，體系總的反應速率常數（kT）可以表示為：

式中，k?是本征反應速率常數，Δk 是反應微環境及其結構演化對反應速率常數的影響。因此可通過改變微環境調控Δk，從而提高反應速率。如表1 所示，在溴丁烷和氰化鈉的取代反應C4H9Br +NaCNC4H9CN + NaBr 中，溶劑發揮著重要的調控作用[10]：溴丁烷和氰化鈉可以發生取代反應，但是如果反應溶劑為甲醇和水時，反應雖可以進行，但反應速率很慢，產率低。若采用二甲基亞砜、二甲基甲酰胺和乙腈作反應溶劑時，其反應速率比以甲醇作溶劑時分別快1300、2800 和5000 倍。從反應?傳遞耦合的觀點來看，化學反應速率還與反應底物濃度、分子擴散速率和催化劑種類、結構和形貌等因素密切相關。而反應溶劑特性既決定了反應底物分子的飽和溶解濃度，也影響了其擴散速率，進而影響反應?分子傳遞耦合的匹配程度，此外，反應溶劑流動速率還影響產物分子的界面脫附、傳遞及反應平衡走向等。以雙氧水的綠色制備為例，氫氣和氧氣通過催化反應生成雙氧水，被視為現行蒽醌法合成技術的綠色替代路線，具有重要戰略意義和應用價值，受到學術界和工業界的廣泛關注。人們開發了多種高活性雙金屬催化劑，但受制于雙氧水反應強放熱特性，該項技術研發陷入了“活性越高越易爆炸”怪圈。分析表明，采用納微反應器并選擇合適的溶劑，可降低催化位點附近反應底物濃度并調控反應－傳遞匹配程度，從而有效規避爆炸風險，并穩定提高反應的選擇性和轉化率。

表1 溴丁烷和氰化鈉的取代反應C4H9Br + NaCNC4H9CN + NaBr在不同溶劑中的相對反應速率［10］Table 1 Relative rate of SN2 displacement of 1-bromobutane by azide C4H9Br + NaCN C4H9CN +NaBr in various solvents［10］

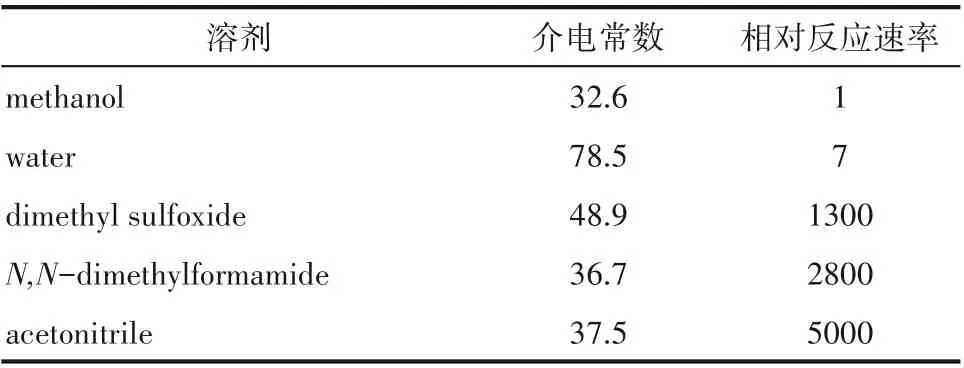
表1 溴丁烷和氰化鈉的取代反應C4H9Br + NaCNC4H9CN + NaBr在不同溶劑中的相對反應速率［10］Table 1 Relative rate of SN2 displacement of 1-bromobutane by azide C4H9Br + NaCN C4H9CN +NaBr in various solvents［10］

溶劑methanol water dimethyl sulfoxide N,N?dimethylformamide acetonitrile介電常數32.6 78.5 48.9 36.7 37.5相對反應速率1 7 1300 2800 5000

迄今為止，國內外研究人員對反應溶劑的影響和調控主要基于經驗或試錯法，對化學反應的溶劑效應嚴重缺乏機理上的理解。困難源自于實驗和理論兩個方面。一方面，實驗上可通過紅外光譜、拉曼光譜、核磁共振、高分辨粉末X 射線衍射（HRPD）等高精度分析手段檢測反應體系中某些關鍵位置的動態原位信息[11?15]，但這些信息往往都是局部的，管中窺豹式的高精度觀測能為機理性理解提供實驗佐證，但難以給出溶劑在熱力學和動力學上對反應影響的完整內在規律。另一方面，液相化學反應中往往涉及電子的轉移和溶劑的結構變化，是典型的介尺度問題。在以往絕大部分研究中，電子、分子等不同尺度上的物理化學過程都是單獨處理或解耦研究的，很少涉及不同尺度之間的耦合與關聯，耦合量子力學和統計力學的介尺度模型缺失。實驗和理論上的困難，嚴重阻滯了復雜化學反應過程中溶劑效應的深入研究，也不利于綠色化工新技術的發展。

反應活化能和反應自由能計算是研究反應機理最重要的途徑之一。從物理化學的角度來看，反應自由能為判斷反應路徑提供了重要的判據，活化自由能的大小則決定了反應發生的概率。本文從溶劑對化學反應自由能分布影響出發，綜述了目前發展的理論模型，并聚焦于本課題組發展的反應密度 泛 函 理 論（reaction density functional theory，RxDFT），分別介紹了RxDFT 的構建及其在水相、有機相、界面體系和限域體系中的應用，分析了不同反應環境對化學反應自由能分布的影響，總結了溶劑效應的影響機制，最后展望了自洽反應密度泛函理論的構建、反應?擴散耦合研究、聚合物反應密度泛函理論及反應密度泛函理論在反應溶劑篩選、界面反應和電解液設計中的應用。

1 溶劑對反應自由能分布影響的研究進展

發展對反應活化能與反應自由能的準確、快速計算一直是計算化學中重要的研究課題之一，到目前為止，人們也發展了多種研究方法[6?8]。總地來說，這些方法可以概括為三大類。第一大類是采用溶 劑 效 應 的 零 階 近 似（zeroth?order approximation）[7?8]，即將溶劑視為連續介質，在計算過程中通過介電常數的參數設置來體現溶劑的性質。目前，大部分的量子化學計算都是采用這種方法[16?17]。這種方法相對簡單且計算成本低，而且對于部分反應，也可以做出定性的解釋。但事實上，在很多化學反應中，特別是溶劑為極性或帶電溶劑，且反應物與產物分子有極性轉變時，考慮溶劑效應后反應自由能有很大的甚至有定性的區別[6,18]。這種區別對于研究反應路徑與反應機理極為關鍵，但難以通過連續介質模型來描述。

第二大類方法是采用經典力學與量子力學耦合的辦法，即最早由Car 等[19]提出的量子力學/分子力學（quantum mechanics/molecular mechanics，QM/MM）模擬方法，把溶劑的影響嚴格地考慮到反應計算過程中[20]。QM/MM 方法原則上可以對反應動力學包括反應路徑等進行嚴格描述。其核心思想是把反應體系分為兩個區域，分而治之并合理考慮兩個區域之間的耦合作用[19?20]。核心區域發生本征反應，該區域（量子系統）一般只包含參與反應的分子、離子（有時也包括部分催化劑）。外面的區域是溶劑系統，不參與到反應中來，但是與量子系統有相互作用，從而影響反應的發生及反應路徑的選擇。對于尚未發生反應的反應底物，也包含在溶劑系統中。溶劑系統可以用分子力學來描述，其對量子系統的影響體現在交叉Hamilton 算子上[20]。對于量子系統來說，Hamilton算子由兩部分組成：

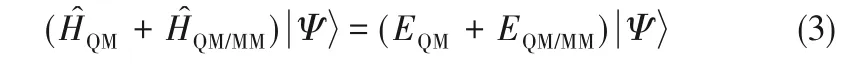
式中，EQM和EQM/MM是對應的能量本征值。很顯然，如果忽略H?QM/MM（或EQM/MM），式(3)就回歸到反應介質效應的零階近似。

QM/MM 計算較為復雜且計算資源需求非常大[21]，其應用受到了較多的限制，而零階近似可能有定性的誤差。因此人們提出了第三類研究方法，即把式(2)中的耦合項H?QM/MM用更高級的統計力學理論來描述[20,22?25]。到目前為止，發展了一系列研究方法，其中包括多構型自洽場理論（MCSCF）[26?27]、溶劑平均靜電勢理論（ASEP）[28?29]、平均場近似（MFA）[30]和RISM/SCF[31]等。在這些方法中，比較引人注意的是RISM/SCF 理論。RISM（reference interacting site?site model）本身是現代經典統計力學中一個比較高級的理論，最初由美國加州大學伯克利分校Chandler 等[32]提出，后經日本Hirata 等[33?35]發展壯大的基于分子水平的積分方程方法。它可以通過自洽的方法快速預測出溶質周圍的溶劑結構，繼而能預測出溶質的溶劑化自由能（solvation free energy，SFE）[36?37]。RISM 與量化計算用自洽的方法結合就發展成為RISM/SCF 理論，最初由Ten?no 等[38?39]提出，到目前為止已經應用到很多反應系統，如研究水的自電離現象[40]、甲酰胺的互變異構現象[41]等。

值得說明的是，上述這些與量子計算耦合的統計力學理論中，自變量是溶劑系統內組元的密度分布，而不是每個溶劑分子的坐標和動量。因此與QM/MM方法相比，這種與統計力學結合的理論有先天的計算效率上的優勢；同時，它又基于較為嚴格的理論基礎，比起溶劑效應的零階近似來說更為合理，適用范圍也更廣泛。在具體計算的過程中，溶劑的結構往往與溶質（反應體系）耦合在一起，需要通過多次迭代后，兩者才會達到最后的自洽[42]。一旦溶質的構型因為反應發生變化，溶劑的微觀結構也會跟著弛豫。這個過程雖然涉及到動力學，但RISM/SCF理論還不能用來描述系統的動力學性質。這可能一方面是因為非平衡態統計理論還在發展之中，另外一方面RISM 理論作為一種積分方程方法，并不適合用來描述諸如擴散等動力學性質。因此，在反應和擴散耦合比較緊密的情況下，需要回歸到QM/MM 方法，或者用更好的統計理論來代替RISM與量子力學結合。在這個方向上，經典密度泛函理論是一個很好的選擇。

經典密度泛函理論與RISM 理論一樣，也是基于分子水平的現代統計力學理論，它是密度泛函理論的一個分支[43]。與量子密度泛函理論（QDFT）依賴于電子密度分布作為泛函變量不同，經典密度泛函理論（CDFT）以系統組分的空間密度分布作為泛函變量，可以預測不涉及化學反應的流體系統的結構和熱力學性質，它的處理結果可以與宏觀熱力學直接聯系起來[44]。基于系統組分的幾何復雜度，已經發展了三種不同類型CDFT：原子DFT、分子DFT和聚合物DFT[43]。顧名思義，原子DFT 可用于研究由球形粒子組成的簡單流體系統[30]。分子DFT 主要是考慮非球形剛性分子的取向貢獻來研究分子流體系統[45]。聚合物DFT 則考慮了聚合物分子的鏈接貢獻[46?47]。盡管這三種不同類型的CDFT 的泛函形式明顯不同，但它們有著相同的變分框架[43]，即系統自由能或者巨勢都可以表達為系統組分密度的泛函。基于此，本課題組將不同尺度下的統計密度泛函和量子密度泛函統一在同一個變分框架下（圖2），提出了多尺度平衡態密度泛函理論的統一框架。該統一框架為界面體系多尺度研究提供了高效模型。

近幾十年來，CDFT 已發展成為化學、化工及相關領域中最強大最多面的計算工具之一，并在計算多孔介質中氣體吸附、受限空間流體等高度非均相流體的結構和熱力學性質等方面展現了快速、精確的計算能力[48?49]。其中，分子CDFT 被用于準確預測溶劑化自由能，最近又被用于快速篩選水合自由能[50?51]。近些年，平衡態密度泛函又推廣到非平衡態，在擴散、吸附、輸運等動力學性質描述方面與動力學模擬相比表現了很好的一致性[52?53]。原子DFT 的動態版本，通常稱為動態DFT，在高性能超級電容器的計算輔助設計中得到了廣泛的發展和應用[54?57]。

Petrosyan 等[58]首 次 提 出 將CDFT 和QDFT 相 結合來考察溶劑對化學反應的影響，且發展了Joint DFT（JDFT）。在JDFT 框架中，自由能泛函可以寫成：

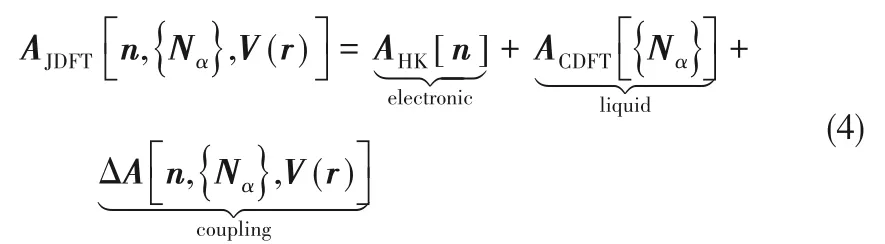
式中，AHK是Hohenberg?Kohn(HK)定理中的電子能量泛函，ACDFT是液體的自由能泛函，ΔA[n,{Nα},V(r)]是溶質與溶劑相互作用有關的耦合自由能泛函。JDFT 通常用極化連續介質模型來處理溶劑，溶劑密度直接從溶質電子密度計算出來，而不是一個獨立的變量[59?60]。溶質和溶劑之間的聯系采用所謂的電子密度泛函方法來描述[60?61]，從而使電子密度成為JDFT 中唯一的變量[61]，但預測的氫氣和氧氣密度分布和實驗結果有明顯的偏差[59]。

本課題組自2014 年以來探索QDFT 與CDFT 結合[43]，發展了反應密度泛函理論，并研究了幾類水相、有機相和限域流體中化學反應的溶劑效應，闡述了溶劑對反應路徑影響的微觀機理，從而為良性反應溶劑選擇和溶劑化效應機理研究提供了可行模型。

2 反應密度泛函理論

2.1 反應密度泛函理論框架

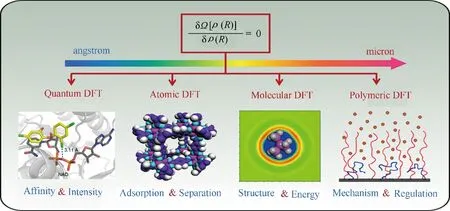
圖2 密度泛函理論統一框架示意圖[43]Fig.2 Schematic graph for the unified framework of density functional theories[43]

在反應密度泛函理論框架下，溶液中的反應自由能FR描述了整個反應的自由能變化，決定了反應能壘高低和體系自由能的變化，它由兩部分構成，即反應分子發生構型變化時的本征能量，以及這種本征反應導致的周圍液相環境微觀結構變化從而引起的液相介質的自由能變化[62?65]。理論上可表示為[6,66]：

式中，ER是本征自由能，也就是忽略溶劑環境發生反應所需要的能量，可采用量子密度泛函計算。ΔFSol表示化學反應發生前后反應體系的溶劑化自由能之差，也就是反應前后溶劑環境的自由能變化，可采用分子密度泛函理論來計算。如圖3 所示，考慮溶劑中的一個典型簡單化學反應A +，則ΔFSol=。當ΔFSol相對較小時，式(5)回歸到溶劑效應的零階近似。

圖3 典型化學反應在氣相和溶液中的熱力學循環（Fsol為反應物/產物分子的溶劑化自由能，ER表示在氣相中的反應自由能，FR表示在液相中的反應自由能）[66]Fig.3 Thermodynamic circle for a representative chemical reaction()occurs in gas phase and in solution(Fsol is the solvation free energies of reagent/product molecules，ER denotes the reaction free energy in gas phase,and FR is the reaction free energy in solution)[66]

2.2 反應自由能和活化自由能

根據過渡態理論（transition state theory，TST）[67]，如圖4（a）中所示，氣相中量子系統在反應前后處于平衡狀態，其自由能分別設為F0和F2。兩者之差即為反應自由能，即ER= F2?F0。假設過渡態系統自由能是F1，則反應自由能壘或活化自由能為EA=F1?F0。相似地，在溶液中反應自由能可以表示為FR= F′2?F0。如圖4（b）所示，反應自由能壘或活化自由能為FA= F′1?F0。由式(5)可知，由于本征反應與溶劑效應的解耦，FR和FA可以通過將相應的本征反應自由能ER和EA與溶劑化自由能差相加得到。

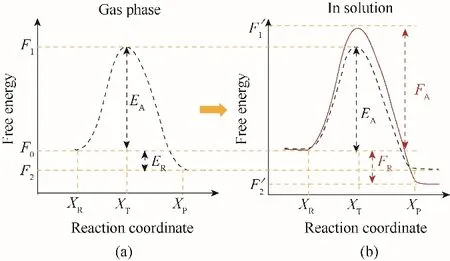
圖4 在氣相中（a）和在溶劑中（b）的反應的典型自由能分布（過渡態與反應物之間的能量差為反應的自由能壘或活化自由能，其代表了一個反應系統發生所必須獲得的最小能量。生成物和反應物的能量之差為反應的自由能）[66]Fig.4 Typical energy profiles for a reaction in gas phase(a)and in a solvent(b)(The difference between the energies of transition state and reactant is the energy barrier or activation free energy of reaction;it represents the minimum energy that a reacting system must acquire for the transformation to take place.The difference between the energies of the product and the reactant is the free energy of reaction)[66]

在反應密度泛函理論框架下，可假設溶劑的弛豫通常比反應過程快得多[9,68?69]，即溶劑化自由能的計算可以與本征反應自由能的計算解耦。因此，溶劑化自由能可以表示為溶質周圍溶劑密度分布函數的泛函：

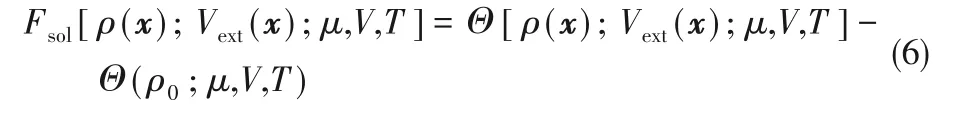
式中，ρ(x)是溶質分子的密度分布，x=(r,Ω)表示溶劑分子的坐標和空間取向。ρ0和μ 分別是溶劑的體相密度和化學勢，V 和T 分別是系統體積和熱力學溫度。體相化學式由體相密度通過狀態方程確定，系統的體積選取需足夠大，其數值并不影響計算結果。在下面的泛函變量符號中省略μ、V 和T。Vext(x)表示溶劑系統的外勢，它來源于溶劑和溶質的相互作用。隨著化學反應的發生，量子體系的分子結構和電荷分布會發生變化，Vext(x)也會隨之發生變化。Vext(x)是由量子系統和溶劑系統之間的分子原子相互作用造成的，和其他多尺度方法一樣，它通常包括庫侖相互作用和Lennard?Jones（L?J）相互作用[31,58]，其表達式為：

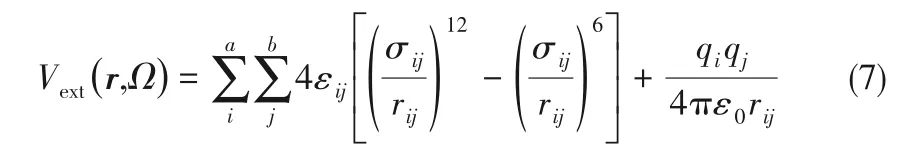
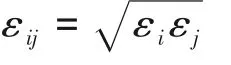
對于給定的Vext(x)，溶劑系統的巨勢可以由式（8）計算得到：

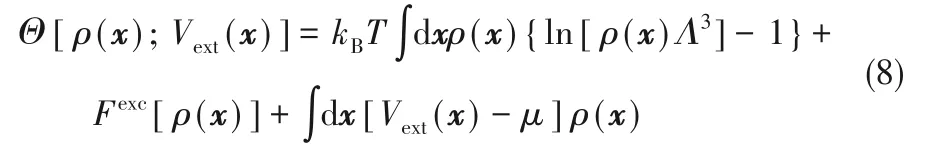
式中，kB是Boltzmann 常數，Λ 是溶劑分子的有效熱波長，Fexc[ ρ(x)]是由溶劑分子間相互作用引起的過剩自由能泛函。到目前為止，已經開發了密度展開的方法和自由能分解法等來構建過剩自由能泛函。

在熱力學平衡條件下，溶劑密度分布使溶劑體系的自由能泛函達到最小。換言之，通過對式(6)中溶劑化自由能泛函最小化，可以得到平衡時的溶劑密度分布和溶質的溶劑化自由能[50,71]，即：

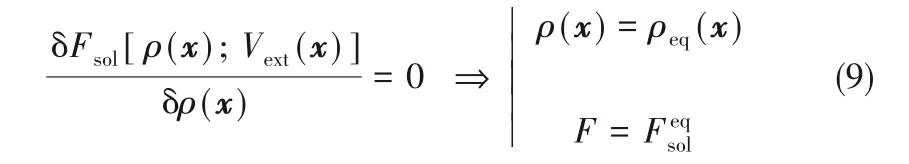
因為CDFT 直接將自由能與系統組分的密度分布關聯起來，從而繞過了冗長的熱力學積分，大大減少了計算成本。這點與分子模擬相比具有明顯的優勢[71]。利用CDFT 可定量預測不同中性溶質和離子的水合自由能[50]。另一方面，與RISM 理論相比，CDFT 的理論框架更加靈活，而且它可拓展到非平衡系統用來描述擴散動力學[54?57]。

3 反應密度泛函理論初步應用

3.1 水溶液對化學反應的影響

3.1.1 甘氨酸水合反應路徑研究 互變異構化現象在化學和生物領域普遍存在[72]。在溶液環境中研究互變異構化已引起了越來越多的理論研究興趣[73?82]。這是因為溶液中的互變異構化反應不僅可作為模型系統來研究，而且這些反應具有實際應用的重要性[83?85]。互變異構化反應也同時可成為生物質能轉化中酮化和醛醇縮合反應甚至分子炸藥分解的決速步[86?87]。

甘氨酸（glycine）是最簡單的氨基酸，白色或淺黃色晶體，易溶于水，有甜味。甘氨酸在氣相或真空中是以中性形式（N）存在的；而在水溶液中，由于與水分子的靜電相互作用，以兩性離子形式（Z）存在。盡管實驗測定從中性形式到兩性離子形式的自由能變化約為?7.3 kcal/mol[73,88]（1 kal=4.18 kJ），但甘氨酸在水溶液中的結構轉變路徑有兩種可能，分別對應兩種反應機制：非輔助協同機制（nonassisted concerted mechanism）和輔助協同機制（assisted concerted mechanism）[82]，兩種反應機制的中間過渡態分別為TS1和TS2。如圖5所示，在非協同反應機制中，中性結構中的氧原子上的氫原子朝向氮原子方向，在過渡態結構（TS1）中氫原子與氮原子形成了很弱的鍵，由兩個碳原子、一個氧原子、一個氮原子和一個氫原子組成一個五元環的結構，之后氫原子與氧原子之間的鍵發生了斷裂，形成了兩性離子結構，完成了質子轉移。在協同反應機制中，水分子作為傳遞氫原子的媒介參加了反應。在中性結構中，氧原子上的氫原子朝向水分子中氧原子，同時氧原子中的一個氫原子朝向氨基乙酸中的氮原子，在過渡態結構（TS2）中由于氧原子上的氫原子與水分子中的氧原子，水分子中的氫原子和氨基乙酸中的氮原子成鍵，由兩個碳原子、兩個氧原子、一個氮原子和兩個氫原子形成了一個七元環結構，之后甘氨酸中的氧原子與氫原子斷鍵，水分子中的氧原子與連接在氮原子上的氫原子發生斷鍵，形成了兩性離子結構，完成了質子轉移[82]。

圖6是采用反應密度泛函理論預測甘氨酸互變異構化反應分別在氣相、水溶液環境中的反應路徑。在MP2、B3LYP、M06?2X 水平上計算本征自由能，得到的自由能分布表明在氣相中的化學反應是吸熱的。RxDFT 預測的非輔助協同機制和輔助協同機制的自由能分布圖表明甘氨酸異構化反應在水溶液中是放熱的。RxDFT 理論預測的結果與文獻報道采用MD/MP2方法的計算結果和實驗測量結果吻合度較好[82]，這表明RxDFT 方法的準確性和可靠性。

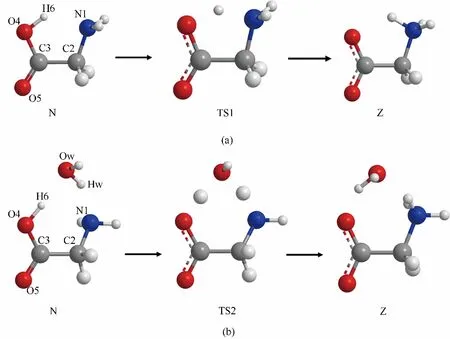
圖5 非輔助協同機制（a）和輔助協同機制（b）中甘氨酸中性、過渡態和兩性離子結構的示意圖[66]Fig.5 Schematic representations and atomic numbering for the neutral,transition,and zwitterionic structure of glycine with nonassisted concerted mechanism(a)and assisted concerted mechanism(b)[66]

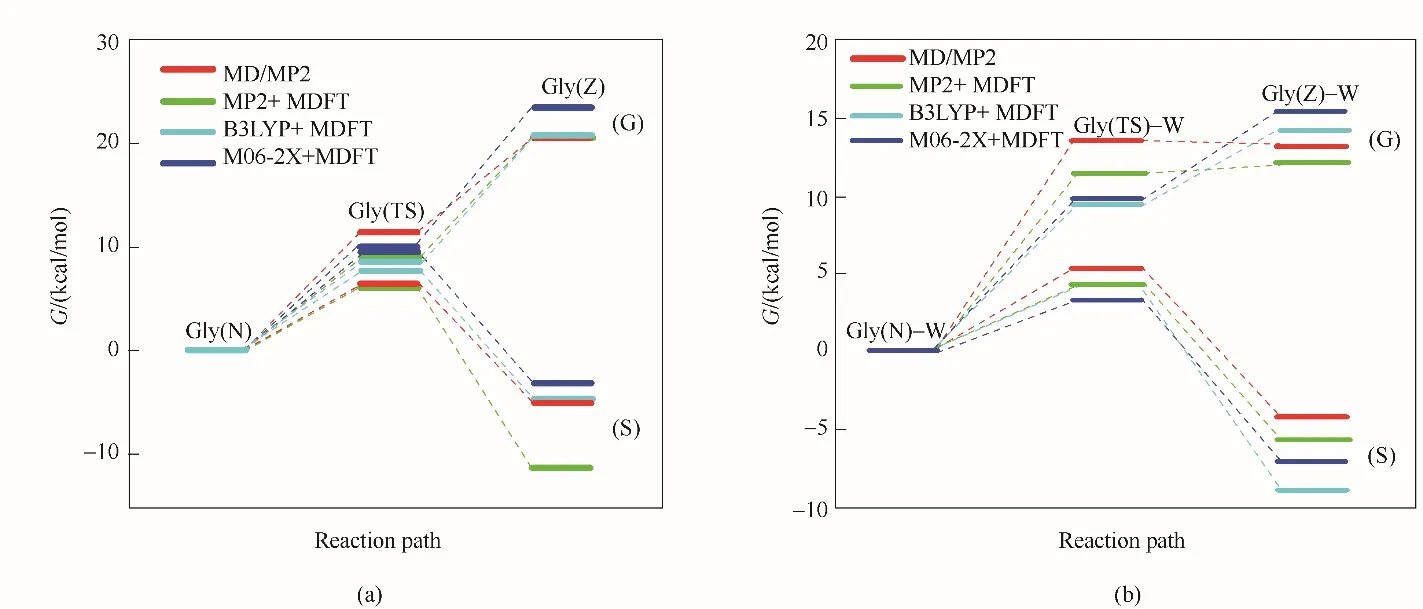
圖6 非輔助協同機制（a）和輔助協同機制（b）的甘氨酸自由能分布圖[66]（G表示氣相反應，S表示水溶液反應。MD/MP2方法的自由能分布來自文獻[82]）Fig.6 Free energy profiles for glycine using a nonassisted mechanism (a)and an assisted mechanism(b)[66](The label G denotes the reaction in gas phase and S denotes the reaction in aqueous solution.The free energy profiles of MD/MP2 method are taken from Ref.[82])

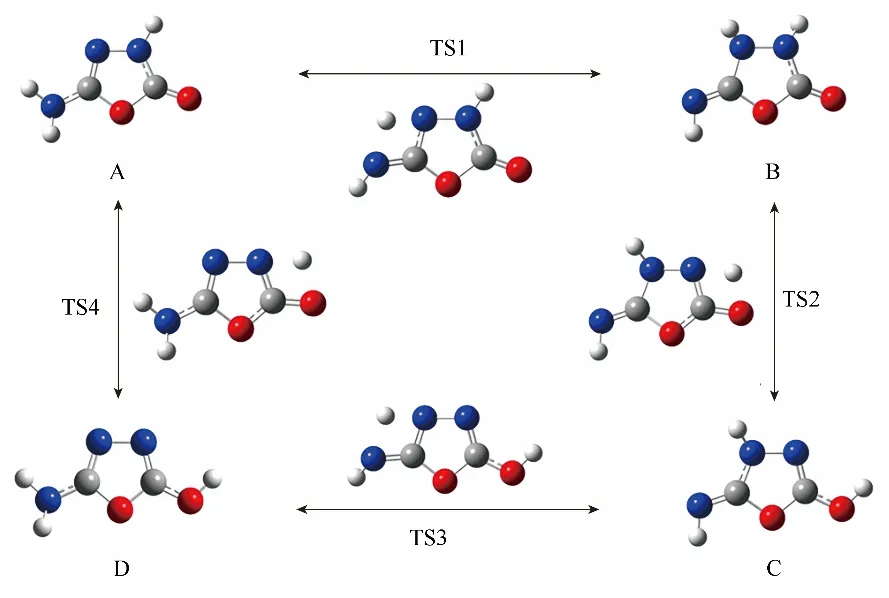
圖7 四個互變異構體（A、B、C、D）與相應的過渡態（TS1、TS2、TS3、TS4）之間的反應方案（AOO的分子結構是在沒有水分子參與的情況下展現的）[96]Fig.7 Reaction scheme among the four tautomers(A,B,C,and D)with the transition states(TS1,TS2,TS3,and TS4)(The molecular structures of AOO are depicted in the absence of water)[96]

對于簡單的互變異構化反應，氣相和水溶液中幾何優化和能量分析表明，異構體A 和C 分別是最穩定和最不穩定的。四個異構體之間的穩定性順序是A > B > D > C。如圖8 所示，溶劑效應使所有簡單互變異構化反應的自由能壘都增加，使B →C和C →D 異構化反應自由能增加，使A →B 和C →D 反應自由能降低。如圖9 所示，對于水協助的互變異構化反應，水分子的協助降低了B →C 和C→D 異構化反應的反應自由能，增加了A →B 和D →A 異構化反應的反應自由能。在水分子的協助下，所有反應路徑中的自由能壘都大大減少。而且這些趨勢與水分子的數量無關。水分子的協助作用可以歸結為兩個相反的效應，即過渡態環的大小和氫位移步效應，且二者競爭協調，當兩個水分子參與協助時，能壘最低。其次，分析了溶劑對水分子協助互變異構化反應的影響，發現溶劑可以進一步降低反應的自由能壘，雖然不是所有反應的自由能都降低。一般來說，水溶液的存在主要是通過水分子的協助作用和溶劑化效應來降低自由能壘。溶劑化效應對自由能壘幾乎沒有貢獻，溶劑分子的協助作用對互變異構化反應的溶劑效應起主導作用。

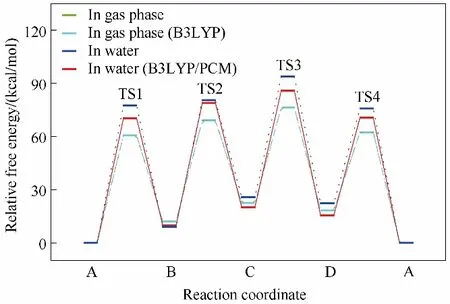
圖8 氣相和水溶液中非輔助協同機制互變異構化反應的自由能分布（青色曲線與綠色曲線互相重疊。溫度298.15 K）[96]Fig.8 Free energy profiles for the nonassisted mechanism tautomerization reactions in the gas phase and aqueous solution(It should be noted that the cyan curve overlaps and the greencurve.The temperature is 298.15 K)[96]

3.1.3 水溶液對SN2 反應的影響 雙分子親核取代反應是構建官能團最常見、最有價值的反應之一，因此在化學和生物化學中具有重要意義[97?98]。在X?++Y?反應中，根據親核試劑X?和離去基團Y?的不同，可以將SN2 反應分為兩大類：對稱（Type Ⅰ）和非對稱（Type Ⅱ）SN2 反應。顧名思義，對稱SN2 反應中的親核試劑和離去基團是一樣的，而非對稱SN2 反應中親核試劑與離去基團不同[99]。SN2反應的反應機理最早由Ingold[100]在1953年提出，隨后Brauman 等[101?102]提出了SN2 反應的詳細原子模型。這個模型假設在氣相中反應首先形成X?…CH3Y 離子?偶極復合物（ion?dipole complex，IDC），然后X?…CH3Y離子?偶極復合物越過能壘形成XCH3…Y?離子?偶極復合物或者分解成反應物。

圖9 水溶液中0～3個水分子參與的互變異構化反應的自由能分布（溫度為298.15 K）[96]Fig.9 Free energy profiles for the assisted mechanism tautomerization reaction in the absence and presence of 1—3 water molecules in aqueous solution(The temperature is 298.15 K)[96]

自由能分布是研究反應機理和揭示反應動力學的重要性質之一[97,103?104]。由于SN2 反應對周圍溶劑的存在很敏感，所以這些反應在氣相和在溶液中的自由能分布有很大的差別[105]。如圖10所示，在氣相中SN2 反應通常沿反應坐標具有雙阱自由能分布。自由能分布圖有一個單一的過渡狀態（TS）和兩個能量最小的穩定態，這兩個穩定態對應于兩個能量穩定的IDC[106?107]。然而，在溶液中，這兩個能量最小的穩定態完全消失不見了，自由能分布圖的兩端是平整的，并且在反應物和生成物之間存在一個巨大的自由能壘[107]。此外，據報道，在質子溶劑中SN2 反應的速率常數比在非質子溶劑中要小幾個數量級（表1）[10,108]。

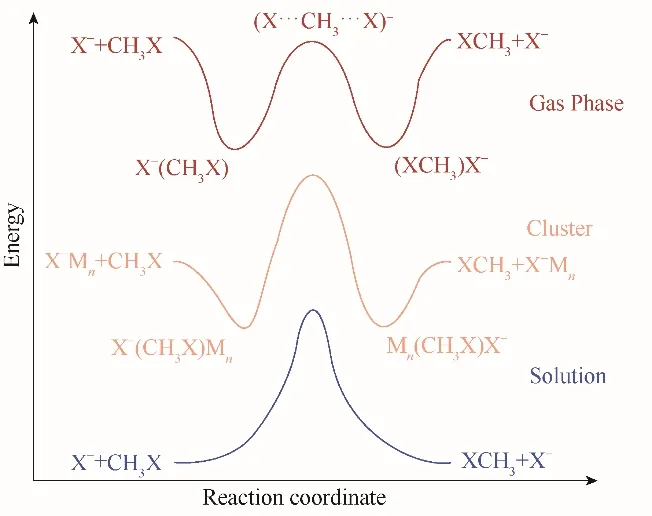
圖10 碘離子與碘化甲烷反應的中間產物的微水化效應[107]Fig.10 Microhydration effects on the intermediates of the SN2 reaction of iodide anion with methyl iodide[107]

在氣相和在溶液中調查對稱和非對稱SN2 反應引起了廣泛的實驗和理論研究興趣[99,107]。Chandrasekhar 等[105]證明了水溶液對典型的對稱SN2反應Cl?+ CH3ClClCH3+ Cl?的自由能分布有顯著影響。Doi 等[107]采用紅外光解光譜（IR photodissociation，IRPD）闡 明 了 微 溶 劑 化 對I?+CH3IICH3+ I?SN2 反應的作用。對于非對稱SN2 反 應，Gao 等[109?110]采 用QM/MM 方 法 得 到 了NH3+ CH3ClNH3CH+3+ Cl?SN2 反應的二維自由能面。他們的研究結果表明，溶劑效應對產物和過渡態具有很強的穩定性作用。這是由于在反應過程中發生了大量的電荷分離。此外，還有很多實驗采用流動余輝（flowing afterglow）技術研究了溶劑對SN2 不對稱反應的影響[111?116]。盡管化學反應在溶液中的實驗技術和預測模型取得了令人滿意的進展，但目前溶劑效應對化學反應影響的潛在分子機制仍不清楚。這個挑戰主要來自于反應子系統與溶劑環境之間復雜和動態的相互作用。

如圖11 所示，采用RxDFT 考察了對稱SN2 反應Cl?+ CH3ClClCH3+ Cl?和 非 對 稱SN2 反 應NH3+ CH3ClNH3CH3++ Cl?的自由能分布。對于對稱SN2反應，量子DFT在M06?2X理論水平上獲得的氣相的本征自由能分布圖具有一個穩定的IDC 的雙阱自由能分布。在水溶液中，活化自由能增大，而雙阱的能量分布則由于TS 和IDC 在溶劑中的不穩定而消失。對于非對稱SN2 反應，它在氣相中是吸熱反應。然而，它在水溶液中變成了放熱反應，伴隨著活化自由能的減少以及過渡態位置的位移。對于這些SN2 反應，RxDFT 預測的活化自由能和反應自由能與QM/MM和實驗數據的結果一致。

3.2 乙腈溶液對SN2反應的影響

圖12 和圖13 為采用RxDFT 方法預測的八個對稱SN2 反應和四個不對稱SN2 反應在乙腈溶液中的自由能分布。如圖12 所示，在所選的八個對稱SN2反應中，不同的烷基氯化物在氣相中的活化自由能差異很大。每增加一個甲基的取代都會增加活化自由能，這些都是空間位阻效應引起的。在乙腈溶液中，極化效應降低了約6 kcal/mol 的自由能壘，溶劑化效應提高了約18 kcal/mol 的自由能壘。因此，溶劑化效應對自由能壘起主導作用。如圖13所示，所選擇的四種不對稱SN2 反應，由于環境溫度下它們具有較高的自由能壘和吸熱的反應自由能，因此在沒有催化劑或溶劑輔助下，它們顯然是不容易發生的。在乙腈溶液中，由于溶劑作用使過渡態和產物更穩定，活化能壘顯著降低，反應變為放熱反應。極化效應和溶劑化效應都使自由能壘和反應自由能降低，而且溶劑化效應起主導作用。對于這些SN2 反應，可以看出RxDFT 預測的活化自由能和反應自由能與用直接與熱力學循環方法結合SMD?M062X 溶劑化模型、Monte Carlo 模擬和實驗得到的結果比較吻合[119?121]。

3.3 固液界面對親核加成反應自由能分布的影響

固液界面處發生的化學反應往往會展現出不同于均相化學反應的性質。為了探究固液界面處的復雜溶劑效應，本課題組將RxDFT 方法拓展到氫氧根與甲醛在類石墨烯基底附近反應的研究中。通過RxDFT 方法計算了反應物、過渡態和產物在距離固體基底不同距離時的溶劑化自由能，發現溶質距離固體基底越近溶劑化自由能越小；計算了溶質在距離固體基底不同距離時周圍的溶劑密度分布，發現當距離較小時基底和溶質附近水的波動發生重疊，這種重疊關系導致了溶劑化自由能的降低；計算了溶質在距離固體基底不同距離時的反應自由能和反應活化能，發現當反應核心區域貼近基底時，反應活化能相較于體相環境中的能量值有所降低（圖14）。這意味著該反應更容易發生在石墨烯?水的界面附近[70]。

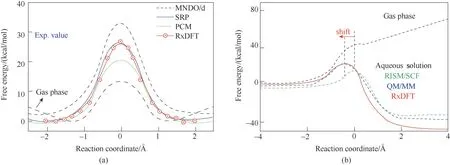
圖11 對稱SN2反應Cl?+ CH3Cl ClCH3 + Cl（?a）和非對稱SN2反應NH3 + CH3Cl NH3CH3+ + Cl（?b）的自由能分布(1 ?=0.1 nm)[117]Fig.11 Free energy profile for the symmetric Cl?+ CH3Cl ClCH3 + Cl?(a)and asymmetric NH3 + CH3Cl NH3CH3+ + Cl?(b)SN2 reaction in aqueous solution or in the gas phase[117]

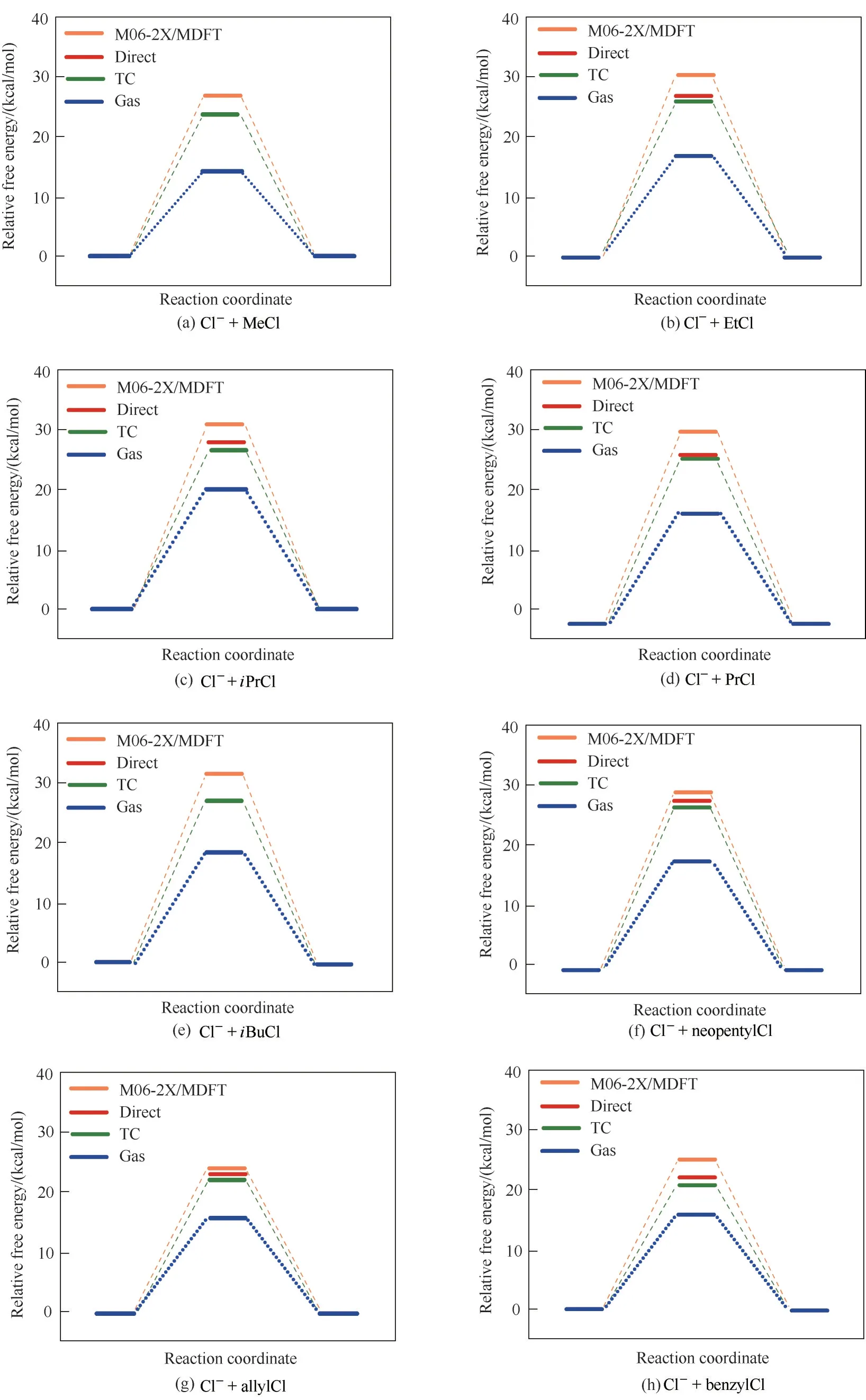
圖12 八個對稱SN2反應的相對自由能分布（溫度為298.15 K）[118]Fig.12 Relative free energy profiles for the eight selected symmetric SN2 reactions in gas phase and in the acetonitrile solution(The temperature is 298.15 K)[118]

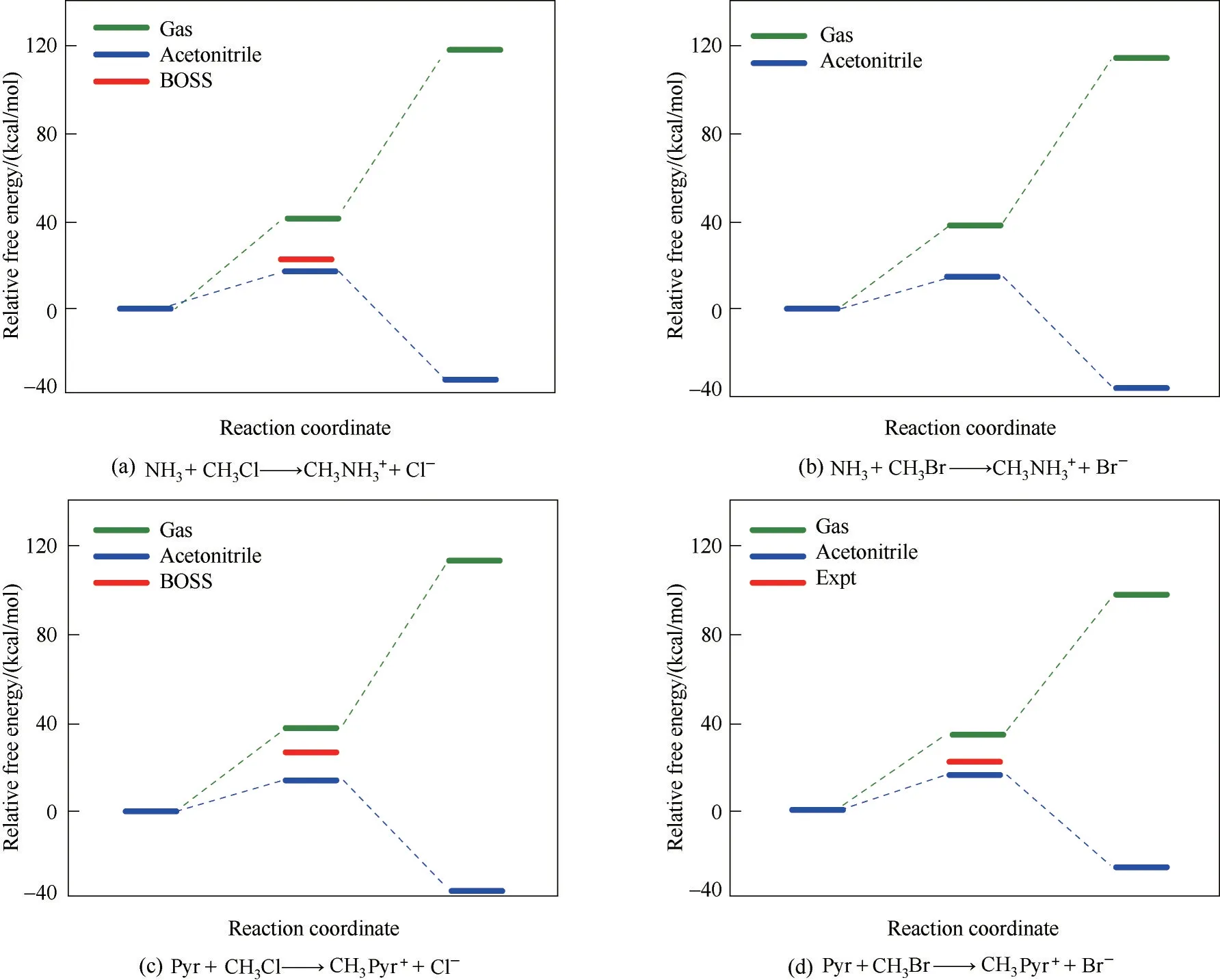
圖13 四個非對稱SN2反應的相對自由能分布（溫度為298.15 K）[118]Fig.13 Relative free energy profiles for the four selected asymmetric SN2 reactions in the gas phase and acetonitrile solution(The temperature is 298.15 K)[118]

圖14 反應自由能（a）和活化自由能（b）隨團簇與界面之間距離的變化[70]Fig.14 Reaction free energy(a)and activation free energy(b)as a function of the cluster?wall distance[70]

3.4 表面潤濕對受限空間流體溶劑化效應的影響及其應用

當反應發生在受限空間溶劑環境中時，在受限空間流體溶劑化效應的影響下，會呈現與均相溶劑中不一致的反應路徑或反應機理[122?123]。烷烴分子構象轉變是一種特殊的反應。據報道，烷烴分子在不同的溶液體系中可呈現出直鏈（extended）?螺旋（helical）構象轉變的現象[124?125]，這種構象的轉變可以在實際中有多種用途，比如選擇性分子識別[124,126]以及分子自組裝等[127]，研究烷烴分子構象轉變的微觀機理以及表面潤濕調控機制對實際應用中對分子構象精準調控有重要指導意義。為了給出烷烴由直鏈構象轉變為螺旋構象的微觀機理，采用RxDFT 方法的框架研究不同孔寬度、壁面潤濕性等不同受限效應對不同鏈長的烷烴分子構象轉變的影響。如圖15所示，烷烴分子在孔徑較小的納米圓管水溶液中更易形成螺旋構象。圓管管壁潤濕性越強，即管壁越親水，烷烴分子越傾向于由直鏈構象轉變為螺旋構象，且烷烴分子鏈越長，這種轉變傾向越明顯。當孔徑較小時，螺旋烷烴與直鏈烷烴系統的巨勢之差隨孔徑變化而“振蕩”變化，即烷烴分子構象隨孔徑變化呈現“直鏈?螺旋”的交替變化現象，隨著孔徑增大，烷烴分子逐步恢復穩定直鏈構象。本節中所做的理論預測結果能夠與前人的實驗結果很好地吻合。

4 未來展望

4.1 自洽反應密度泛函理論的構建

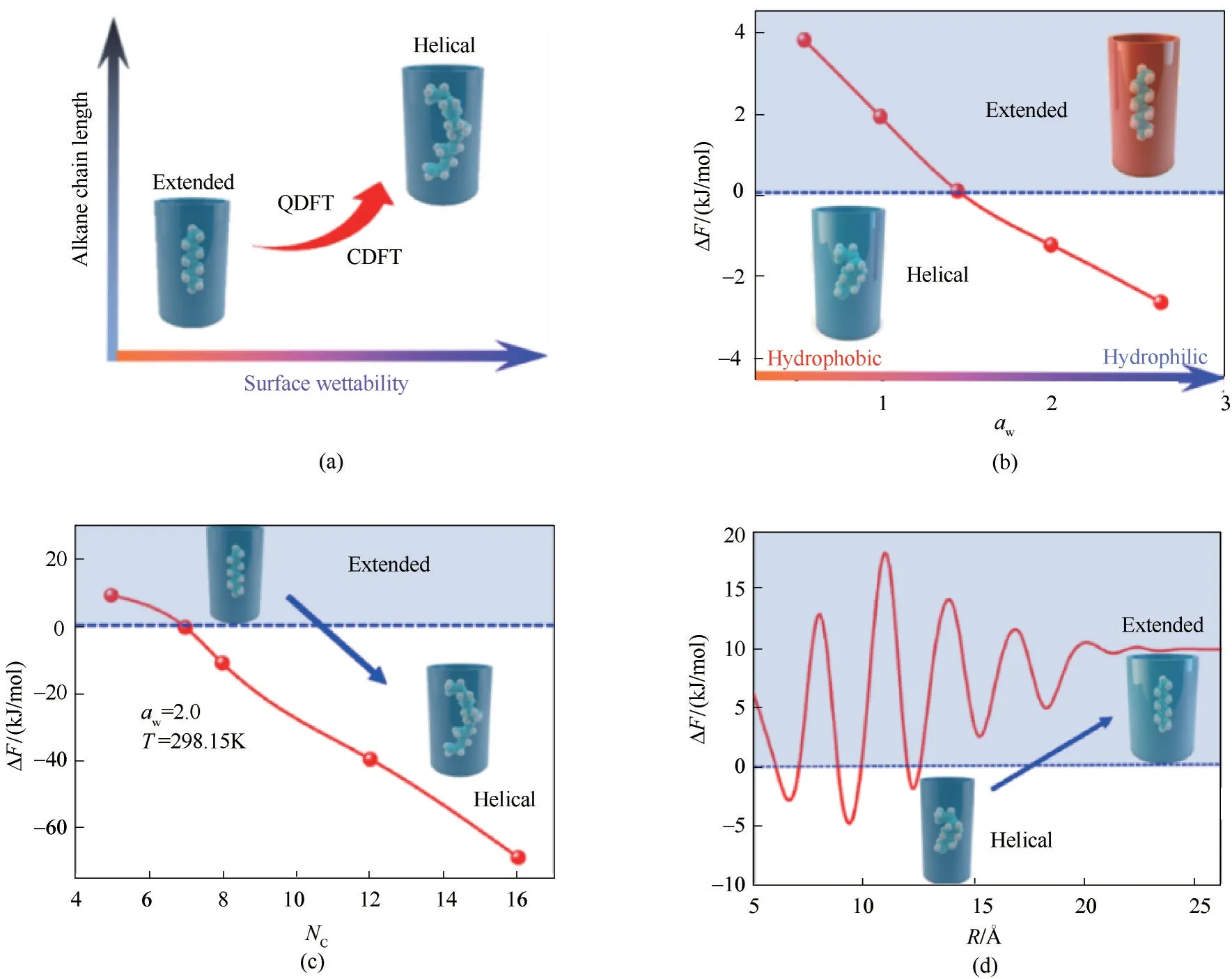
圖15 單個烷烴分子在充滿水的空腔中的構象變化（a）；充滿水的圓柱孔中庚烷的巨勢差隨孔內表面潤濕參數的變化曲線（b）；在充滿水的圓柱孔中的巨勢差隨烷烴分子碳鏈長度NC的變化曲線（c）；充滿水的圓柱孔中庚烷的巨勢差隨孔徑大小的變化曲線（d）[128]Fig.15 Conformational change of a single alkane molecule confined in water?filled cavitands (a);Grand potential difference of heptane in water?filled cylindrical pore varying with the wetting parameter of the pore inner surface (b);Grand potential difference of alkane molecule with varying NC in water?filled cylindrical pore(c);Grand potential difference of heptane in water?filled cylindrical pore varying with the pore size(d)[128]

目前，RxDFT框架下的QDFT和CDFT的耦合模式僅限QDFT 對CDFT 的單向參數傳遞。在RxDFT具體的計算過程中，僅將QDFT 方法計算得到反應體系的結構參數、各原子的偏電荷結合各原子的L?J 參數，作為外勢參數輸入CDFT 進而計算得到反應體系周圍溶劑分子的密度分布ρ(x)和溶劑化自由能Fsol。此時的溶劑分子密度分布相對于初始狀態已經發生了變化，該變化并沒有反饋到QDFT 的計算中，導致溶質分子的波函數沒有得到溶劑的充分極化，CDFT與QDFT在RxDFT理論框架下并沒有達到最終的自洽。如果溶劑分子為較小剛性分子，溶劑分子產生的電場對溶劑分子的密度分布影響并不大，此時沒有QDFT與CDFT間的迭代耦合也可以實現相當不錯的計算精度。當溶質分子為較大的柔性分子時，溶劑分子產生的電場對溶劑分子密度分布的影響就不能忽略，此時QDFT和CDFT間的迭代自洽對于RxDFT 的計算精度就顯得尤為重要。在下一階段，擬將基于RxDFT 方法發展為一種自洽反應密度泛函理論(self?consistent reaction density functional theory，sc?RxDFT)方法。

要實現sc?RxDFT 框架下的QDFT 和CDFT的迭代耦合，需要實現兩方面的自洽。首先是溶劑對溶質分子軌道充分的極化。在QDFT 計算中，溶質分子的溶劑化可以通過在其Fock 算符后加上一個溶劑化修正項來實現，該修正項可表示為溶劑密度分布的函數，溶劑密度分布則通過CDFT 求解得出；另一方面是溶質分子形成的電場對溶劑分子密度分布產生影響。在CDFT計算中，把QDFT計算得到的溶質分子的原子偏電荷及原子坐標結合原子的L?J參數傳遞給CDFT，進而計算出溶劑化自由能和溶劑新的密度分布。然后再將新的溶劑密度分布傳遞到QDFT 中進行新一輪的計算，這樣經過多次迭代，直至溶質分子自由能和溶劑化自由能實現自洽。具體計算流程請參考圖16。sc?RxDFT 方法的建立將為RxDFT 在化學、化工諸多領域的應用打下堅實的基礎。

4.2 聚合物反應密度泛函理論

經典催化系統往往具有循環利用率低、毒性高和催化效率難以調控等缺點。在催化劑表面鉚接高分子可以克服這些缺點，達到定向調控催化活性的目的。鉚接高分子一般對控制條件（如鉚接密度、高分子鏈長、溫度、壓強和pH 等）的變化具有高度可逆的響應。通過改變控制條件可以精確控制高分子的體積、形狀、表面積、溶解度和力學性能等性質。這些高度響應的性質可以用來改性催化劑表面，達到調控催化反應的目的。目前人們對表界面性質與納微結構的關系、界面作用機理和反應動力學過程等仍然缺乏足夠的認識，研究的難點主要在于原位實驗觀測手段（特別是微觀或介觀的手段）的缺乏或不夠精確，而常規的實驗試錯法難以獲得高分子表面改性與反應效率之間的完整構效關系。聚合物密度泛函理論適用于聚合物體系，銜接了微觀結構性質和宏觀熱力學性質，是研究聚合物表界面調控的重要理論工具。其以聚合物的空間密度分布為變量，把自由能和系統組元密度分布直接聯系起來，通過求泛函極值，可同時獲得宏觀熱力學和系統組元的空間密度泛函。然而，相對于平衡態體系，描述非平衡態條件下化學反應的聚合物反應密度泛函理論亟待完善和發展。這一方面是因為聚合物具有復雜的鏈構型分布，另一方面是由于聚合物體系具有多尺度性，從理論上描述聚合物體系的化學反應具有一定的難度。從分子尺度建立聚合物反應密度泛函理論，研究催化反應中聚合物改性對表面催化反應速率的影響機制，考慮鉚接聚合物與反應物、產物分子之間的相互作用，總結控制條件對反應效率的影響規律，具有重要的理論和應用價值。

4.3 反應-擴散耦合研究

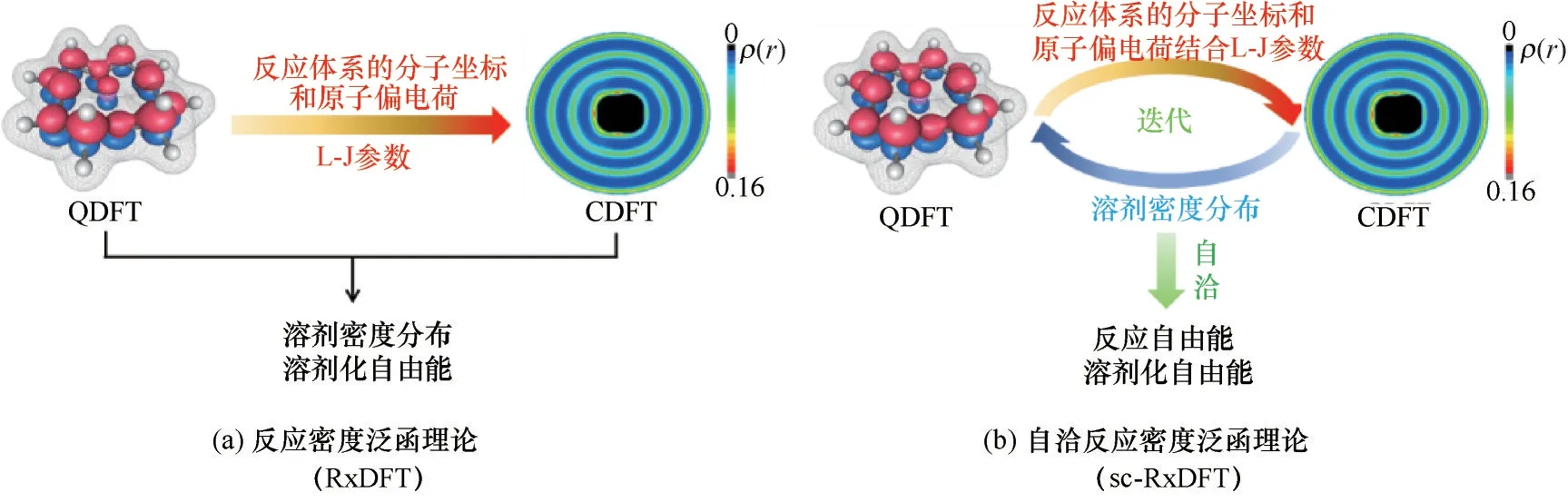
圖16 RxDFT和sc?RxDFT的計算流程圖Fig.16 The scheme of RxDFT and sc?RxDFT

反應?擴散（reaction?diffusion，RD）過程在化工、催化、材料加工和生物領域普遍存在[129]，是化工過程、分離、催化反應等動力學過程中最重要和最基本的過程之一，在化學工程的核心“三傳一反”中占據重要地位，對化工過程中反應分子的微觀傳遞行為及催化劑內部發生的化學反應的深入研究有助于化工反應器和催化劑及化工過程的設計。成功設計新的催化劑和反應器需要掌握催化劑反應微孔空間內分子的催化反應與分子擴散的耦合效應，可以說，由限定在催化劑表界面及孔道內分子發生的化學反應及與擴散協同構成的復雜過程，涉及“三傳一反”理論框架在具有非均勻結構體系中的拓展應用，是當前化工學科中最富挑戰性的研究方向之一。然而，目前反應?擴散耦合主要是采用宏觀擴散理論與反應理論來耦合研究。這種耦合方法雖能解決一些體相的反應問題，但對于界面反應，理論預測與實驗結果相差較大[130]。根本原因在于這些宏觀理論對于界面體系（特別是組元密度分布高度非均相的界面體系）的性質描述不夠準確。在界面區域，流體密度高度不均勻，需要采用分子層面的理論才能對反應?傳遞耦合進行合理描述。而大部分反應過程為界面反應，如界面催化等，界面的屬性影響反應與傳遞的耦合，改變界面性質調控反應?傳遞耦合是提高化工反應效率的重要途徑之一。因此，發展面向表界面體系的反應?擴散耦合理論研究具有十分重要的意義，具有極大的潛在應用價值。

4.4 RxDFT在反應溶劑篩選及界面反應中的應用

催化反應是化學工程的核心組成，是實現物質轉化、工業生產的重要步驟。迄今為止研究人員針對氣?固反應中催化劑的開發和負載，發展了各種性能優越的催化劑和巧妙的催化顆粒/基團負載方式；而對于液?固反應或氣?液?固三相反應，反應的溶劑調控就顯得尤為重要。在這些催化反應過程中，溶劑效應既影響反應體系組元分子的空間密度分布，也影響了其反應?傳遞耦合的匹配程度。具體體現在對催化位點周圍反應物局部密度（溶解度）的調節，對反應物、產物分子擴散動力學特性的改變，以及對傳熱效率的影響等。

基于研究人員的經驗積累和實驗試錯，人們發展出一系列綠色反應溶劑，如超臨界二氧化碳、離子液體等，但目前仍缺乏對溶劑效應的深入理解。因此針對納微界面反應，溶劑調控反應效率目前沒有相關理論依據支撐，找到合適溶劑是一個高成本、高耗時的過程。理論計算是這一問題的解決方案之一。然而，目前針對界面反應，常用的軟件要么不考慮溶劑的作用要么采用極化連續模型處理溶劑效應。例如，在VASPsol 中，通過向Poisson 方程中添加與電子密度分布相關的介電函數來體現溶劑對化學反應的影響，且需要預先設定大量的合理參數來提高計算的準確性[131]。因此，RxDFT 在界面催化領域具有巨大的潛在應用價值。同時，將RxDFT 并入現有軟件有利于其推廣和應用，加速反應溶劑的篩選，為高選擇性和高轉化率的實現和突破提供思路。

4.5 RxDFT在電解液設計中的應用

電解液是電化學電池和超級電容器的重要組成部分。在電解液中，由于離子與溶劑分子的強相互作用，離子總是以溶劑化的形式存在，且溶劑化結構直接影響電解液的穩定性。近年來，溶劑化層中溶劑的作用被不斷認識，并成為電解液設計的一種有效手段。理解電解液溶劑化結構及其構效關系，開發設計更加穩定、高效的電解液體系，是實現電化學電池和超級電容器實用化的必然要求。最近，清華大學張強教授團隊Zhang 等[132]通過在溶劑化層中引入硝酸根陰離子NO?3，形成了更大的溶劑化團簇，并促進雙（氟磺酰基）亞胺陰離子FSI—的分解，形成富含LiF 的界面層，拓寬了電解液的穩定窗口。這些溶劑化過程可以看作離子與溶劑分子之間發生的締合反應。由于涉及到的溶劑種類是多元的，因此需將RxDFT 拓展到混合溶劑體系，發展面向混合溶劑的RxDFT，為高效電解液體系的設計提供理論指導。

5 總 結

液相反應中的溶劑調控是發展綠色化學的重要內容。溶劑對液相反應的能壘、速率甚至反應機理都有重要影響，選擇合適的溶劑已成為調控反應選擇性和轉化率的控制步驟。目前對溶劑的遴選主要基于經驗或試錯，能夠深入描述溶劑對反應自由能影響的定量模型依然缺乏。本文綜述了反應密度泛函理論的構建及其在水相、有機相、界面體系和限域體系中的應用，成功闡述了溶劑對幾類化學反應的影響機理。RxDFT 能夠定量描述溶劑對反應自由能的影響，從而為液相反應中的溶劑化效應機理研究提供了可行模型，為綠色化學發展中的溶劑定向調控提供了理論依據。