數學規劃與圖形方法相結合設計熱集成用水網絡

彭肖祎，董軒，廖祖維，楊遙，孫婧元，蔣斌波，王靖岱，陽永榮

（浙江大學化學工程與生物工程學院，化學工程聯合國家重點實驗室，浙江杭州310027）

引 言

水和能源是工業中必不可少的資源[1?3]，近些年隨著世界能源體系的急速發展，用水和用能集成的問題得到了廣泛關注[4?5]。熱集成用水網絡的設計方法主要有兩大類：數學規劃法[6?12]和概念設計法[13?16]。在數學規劃法的研究中，Du 等設計了逐步優化和同步優化法，有效地解決了用水網絡中的能量集成問題[17]，并且采用分級超結構分步綜合熱集成的質量交換網絡[18]；廖祖維等[19?20]改進轉運模型求解出更優的公用工程費用和換熱匹配數，該模型的規模較傳統轉運模型相比有所減小。而后Zhou等[21]在Liao 等[22]關于流股識別方法的基礎上將順序優化法改進為同步優化法，構建了MINLP 模型和MPEC 模型以降低年度總費用。Yan 等[23]通過更改加熱器和冷卻器的位置，修改了Ahmetovi? 等[24]的超結構模型，從而將公用工程的設計排除在換熱網絡結構之外，他們還提出了不涉及二元變量的流股識別法并且構建了NLP模型。劉祖明等[25]提出了考慮非等溫混合的用水網絡，同時優化水耗以及能耗目標，獲得的換熱網絡結構更為簡單。Hong 等[26?27]提出了包含線性約束和更準確的溫差計算的MINLP模型，并提出了三步求解策略以獲得更好的解，當問題的復雜性增加時，該模型和求解策略的優勢更為突出。在大規模問題的求解上，Lee等[28]探究了連續或批量單元的廠際問題，Rubio?Castro 等[29]通過對園區內廠間現有的用水網絡進行改造，提出了一種新的生態工業廠房設計模型。在最近的研究中，Liu等[30]構建了包含廠內和廠間所有可能出現的水?熱聯結的超結構數學模型，以解決園區內廠間的熱集成用用水網絡的綜合問題。

概念設計法主要是基于Linnhoff 等[31]的夾點設計方法探究公用工程目標以及實現過程集成[32]，被Savulescu[33]率先應用于水和能量的集成研究。后續Savulescu等[34]提出了二維格子圖和構建分離系統兩種圖形方法，先后得到了用水網絡和換熱網絡結構。此后，Leewongtanawit 等[35]提出了水?能源平衡圖，同樣通過構建分離系統的方法改進組合曲線，簡化換熱網絡的設計。此外，源?阱能量復合曲線[36]、質量?能量復合曲線[37]、溫度?濃度[38]序列組合曲線、能量剩余圖[39]等圖形工具也被相繼提出。Feng 等[40?41]分析了非等溫混合對用水網絡的用能的影響，并提出了非等溫混合規則。Hong 等[42]提出了焓?流圖來獲得并聯結構的換熱網絡。隨后，他們又關注到串并聯混合結構的換熱網絡設計，通過在溫?流圖中構建換熱區塊圖[43]和在焓?流圖和溫?焓圖中運用演化的方法[44]分別得到了上述混合結構。近期Chin 等[45]提出了過程圖，根據過程圖可以構造出更為簡單的數學算法以求解熱集成用水網絡模型。

當前，熱集成用水網絡的概念設計法在用水網絡合成階段往往只關注新鮮水和能量的消耗，鮮有文獻考慮投資費用，而這正是數學規劃法的優勢。另一方面，在換熱網絡設計過程中，數學規劃法受到問題規模的制約，難以求解。而概念設計法則可直觀獲得結構簡單、性能優良的換熱網絡結構，但針對已有結構的調優和演化尚未展開。本文將概念設計法與數學規劃法相結合，發揮各自優勢，得到公用工程消耗和總換熱面積都更為經濟的熱集成用水網絡結構。首先應用數學規劃法構建MINLP 模型，得到了公用工程消耗和總換熱面積最小條件下的用水網絡結構。接著應用概念設計法演化該用水網絡的組合曲線以設計換熱網絡結構，最終得到了換熱單元數更小的熱集成用水網絡。

1 熱集成用水網絡的問題描述

熱集成用水網絡的問題描述如圖1 所示：一個工業過程中包含若干個用水單元，每個用水單元對溫度和雜質濃度均有要求，排放的廢水也要滿足溫度標準[46]。上述溫度與濃度的要求通過新鮮水源和公用工程實現。其目的在于：在滿足各個用水單元需求及廢水排放標準的前提下，最小化新鮮水和公用工程的消耗，并簡化換熱網絡。

2 考慮能量集成的用水網絡模型

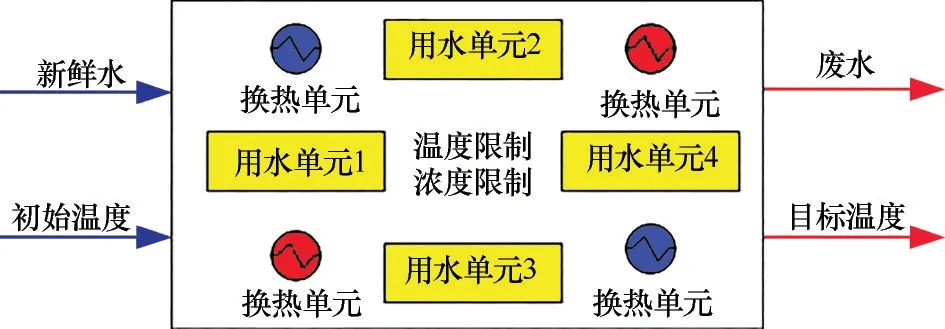
圖1 熱集成用水網絡問題示意圖Fig.1 Illustration of heat integrated water allocation networks

對于圖1 的熱集成用水網絡，每個用水單元除了接收新鮮水源的供給外，在滿足操作溫度和濃度限制的情況下，還可以接收其他用水單元排放的回用水，回用水不循環使用。流入用水單元的新鮮水被視為冷流股，其初始溫度為新鮮水溫度；從用水單元排放的廢水被視為熱流股，其初始溫度為用水單元的操作溫度，目標溫度為廢水排放溫度。基于上述條件建立以下數學模型。

基于用水單元進、出口流股的流量守恒和雜質質量守恒，有如下方程：

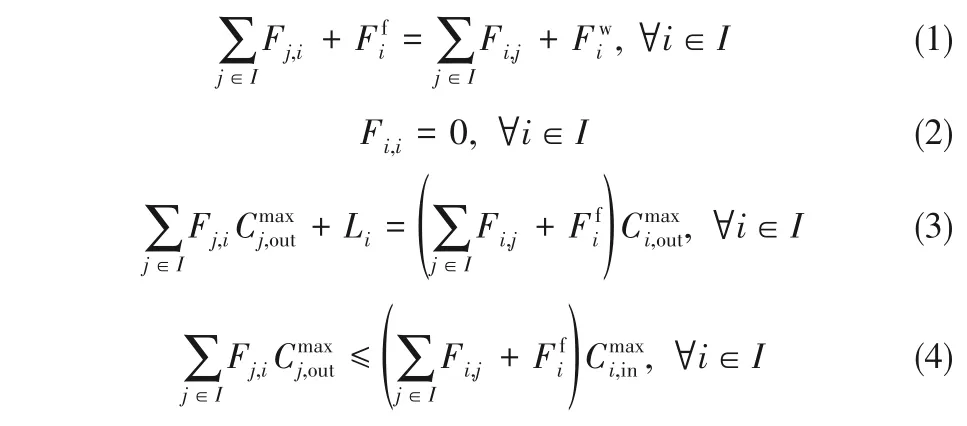
式中，Fj,i代表從用水單元j 流向用水單元i 的回用水流率，kg/s；Fi,i代表用水單元i流向用水單元i的回水流率，kg/s;代表流入用水單元i 的新鮮水流率，kg/s代表用水單元i 排放的廢水流率，kg/s；t和分別代表用水單元j的最大出口雜質濃度和用水單元i的最大進口雜質濃度，μg/L。

基于用水單元進、出口流股的能量守恒，有如下方程：

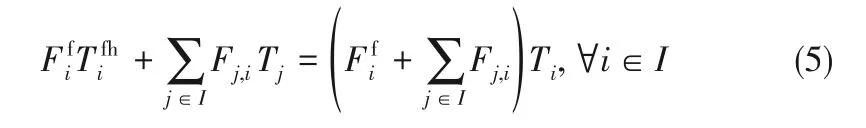
夾點溫度在流股入口溫度之間產生[47]，所以冷、熱流股的入口溫度被視作候選夾點溫度。

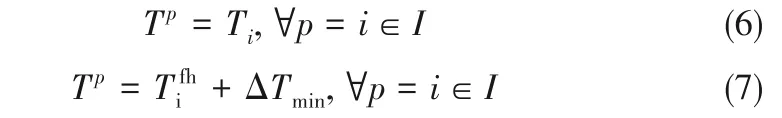
式中，Tp代表候選夾點溫度，℃；ΔTmin代表最小傳熱溫差。

每一個候選夾點p 上方的熱量虧缺Zp的最大值即為最小熱公用工程用量QH（kW）。具體計算方法如下：

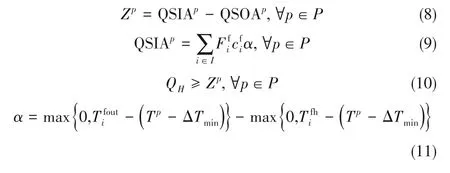
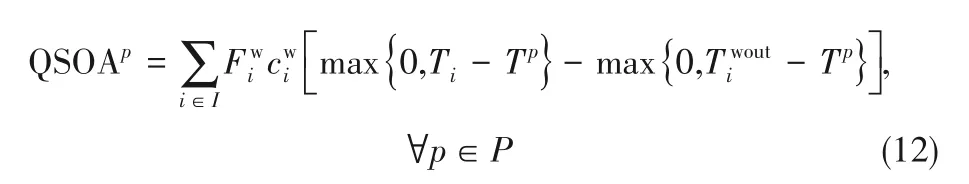
式中，QSIAp代表候選夾點p上方的熱源；QSOAp表示候選夾點p上方的熱阱；Tifout表示流入用水單元i 的新鮮水的目標溫度，℃t表示用水單元i 排放的廢水的目標溫度，℃；和分別表示新鮮水和廢水的比熱容，J/(kg·℃)；表示用水單元i 排放的廢水的流率，kg/s。

冷公用工程的用量QC為熱公用工程的用量QH與流股間回收的熱量Ω之和。

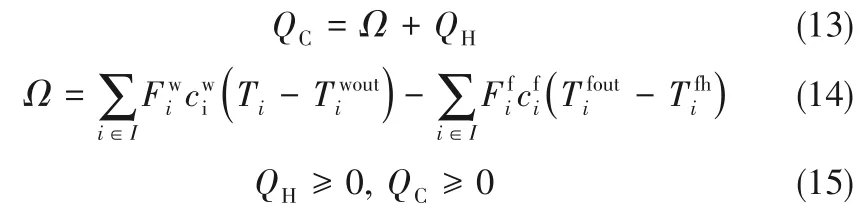
方程式（1）～式（15）用來約束用水網絡的最小公用工程用量，本文將在此基礎上對用水網絡做進一步優化以減小換熱網絡的總換熱面積。流股的相互換熱量固定時，當傳熱溫差增大，換熱面積減小。本文在計算換熱面積時假設相同換熱面積的換熱量相等，那么圖2 所示的分離系統中組合曲線間陰影部分的面積與流股間的換熱量存在式(16)的關系：

式中，SQ為圖2 中陰影部分面積；Qw為冷、熱流股間的換熱量；ΔT 為冷熱流股相互換熱的傳熱溫差。那么換熱器的總面積為：

式中，A為換熱器的總面積；θ為傳熱系數。

為了計算圖2 的陰影面積，首先要確定組合曲線中所有節點的坐標。此時引入二元變量實現冷流股目標溫度的排序，具體方程如下：

k代表溫度節點，Tk是從低到高排序后的冷流股目標溫度，與之間滿足如下約束：

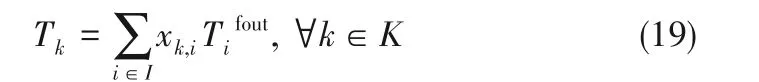
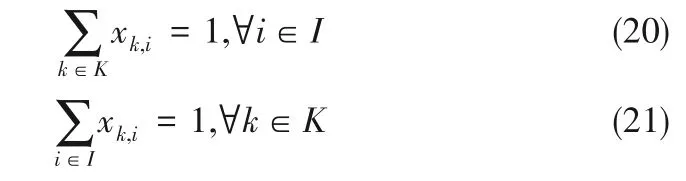
相似地，與Tk相對應的熱容流率FCk滿足如下約束：

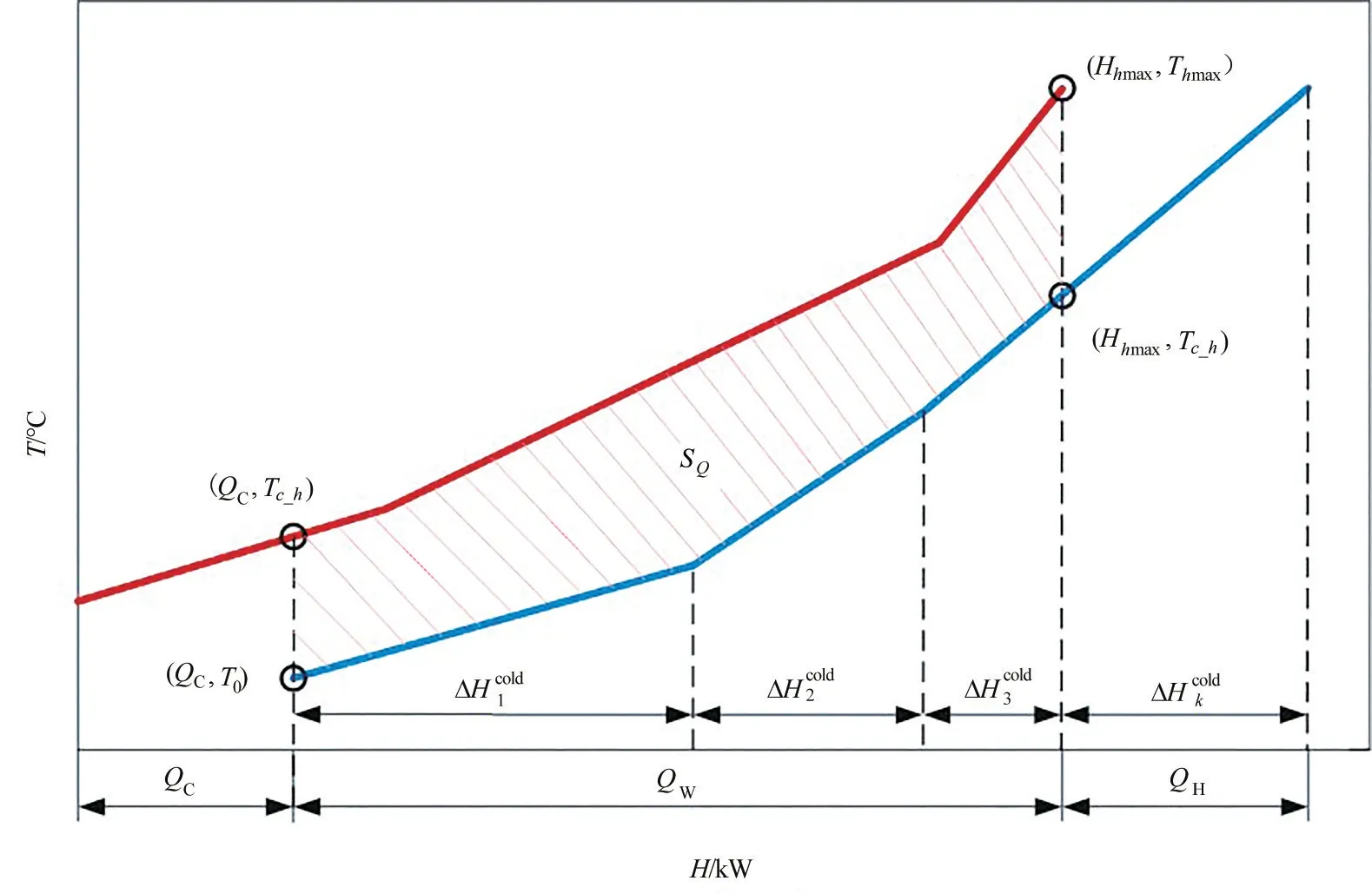
圖2 冷熱組合曲線面積示意圖Fig.2 Schematic diagram of combined curve area

排序后的熱流股入口溫度Th，和相鄰兩個Th之間的焓變的計算方法與冷流股類似。

式中，h 代表溫度節點；Th是從低到高排序后的熱流股初始溫度，與Ti之間滿足如下約束：

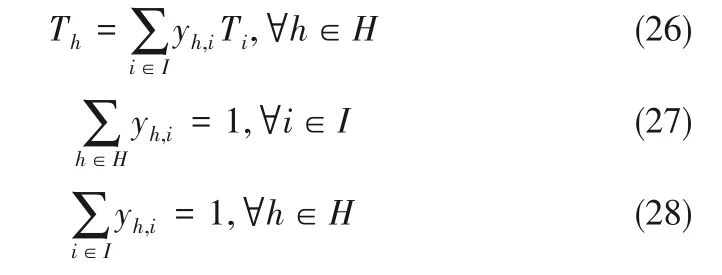
Th相對應的熱容流率FCh滿足如式（29）約束：

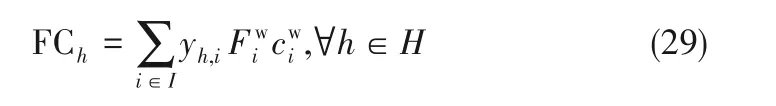
計算相鄰兩個Th之間的焓變，如式（30）所示：

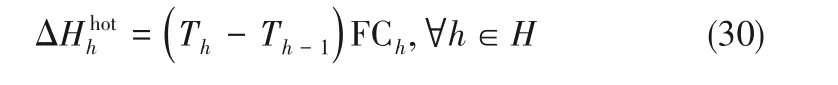
式中，T0=。每個溫度節點h 對應的焓值可由式（31）計算：

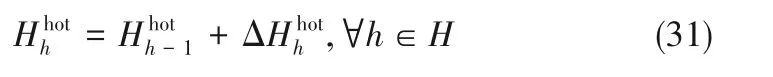
圖2 中，熱組合曲線溫度最高點（Hhmax，Thmax）在冷組合曲線上的投影點坐標為（Hhmax，Tc_h），相似地，冷組合曲線溫度最低點（QC，T0）在熱組合曲線上的投影點坐標為（QC，Th_c）。圖2 中陰影面積SQ等于熱組合曲線中焓值為QC至Hhmax的部分與坐標軸圍成的面積和SH與冷組合曲線中焓值為QC至Hhmax的部分與坐標軸圍成的面積SC之差。SQ與SH按照式（32）、式（33）計算：

Qw滿足如下約束：

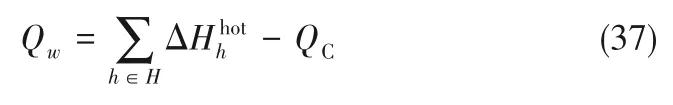
式（11）、式（12）、式（33）、式（34）中的max 函數按照方程式（38）進行平滑處理：

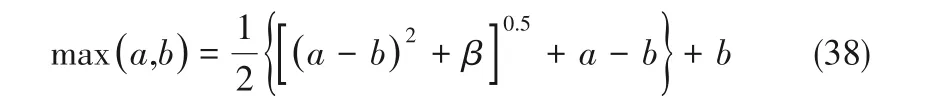
β 是一個很小的常數，通常在10?3～10?6內取值。那么式（11）、式（12）、式（33）、式（34）分別轉化為式（39）、式（40）、式（41）、式（42）。

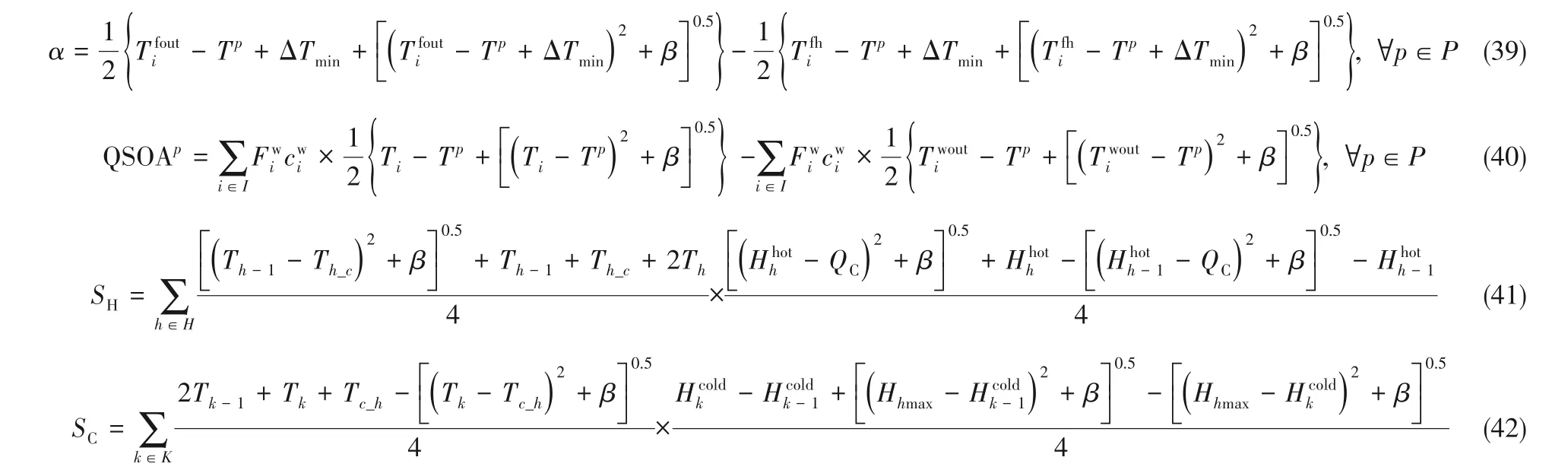
本文數學模型的目標函數為：

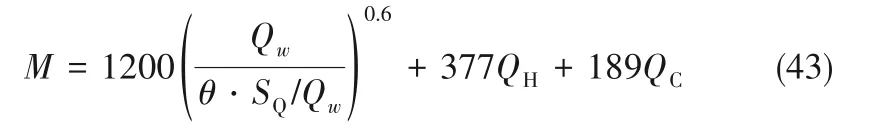
式中，M為換熱網絡的年度總費用，其中單位面積費用為1200 USD/m2，面積成本指數為0.6，冷、熱公用工程的年度費用分別為189 USD/kW、377 USD/kW。

本文以M 為目標函數，方程式（1）～式（10）、式（13）～式（15）、式（18）～式（32）、式（35）～（37）、式（39）～（42）為約束，構建MINLP模型。

以包含四個用水單元的用水網絡為例[35]，完成上述模型的計算。該案例的相關數據見表1。

對上述用水網絡構建本文的MINLP 模型并進行求解，得到該用水網絡的新鮮水用量為90 kg/s，最小熱公用工程為3780 kW，最小冷公用工程為0；根據流股的計算結果可以得到圖3(a)的用水網絡結構圖和圖3(b)的組合曲線圖。

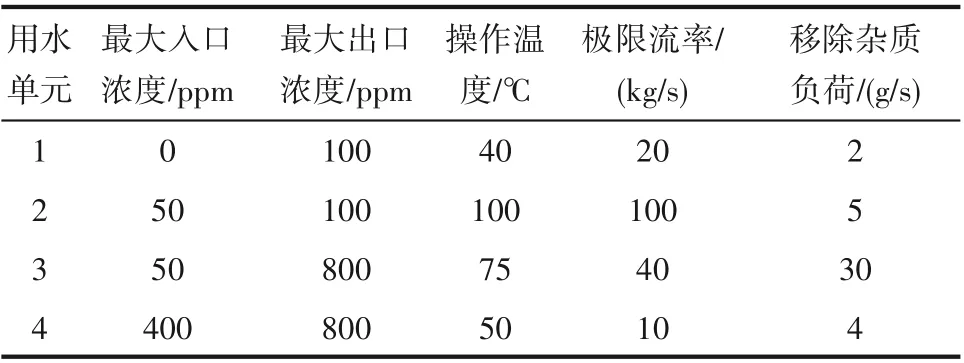
表1 四用水單元的數據Table 1 Water-using operation data

圖3(a)中藍色線段fw1、fw2、fw3 為新鮮水流股，紅色線段ww1、ww2、ww3、ww4 為廢水流股。上述7條冷熱流股在組合曲線中的位置已在圖3（b）中標注出。該組合曲線的夾點出現在圖3（b）的點C 與點H 處。夾點下方冷公用工程為0，夾點上方熱公用工程用量為3780 kW。

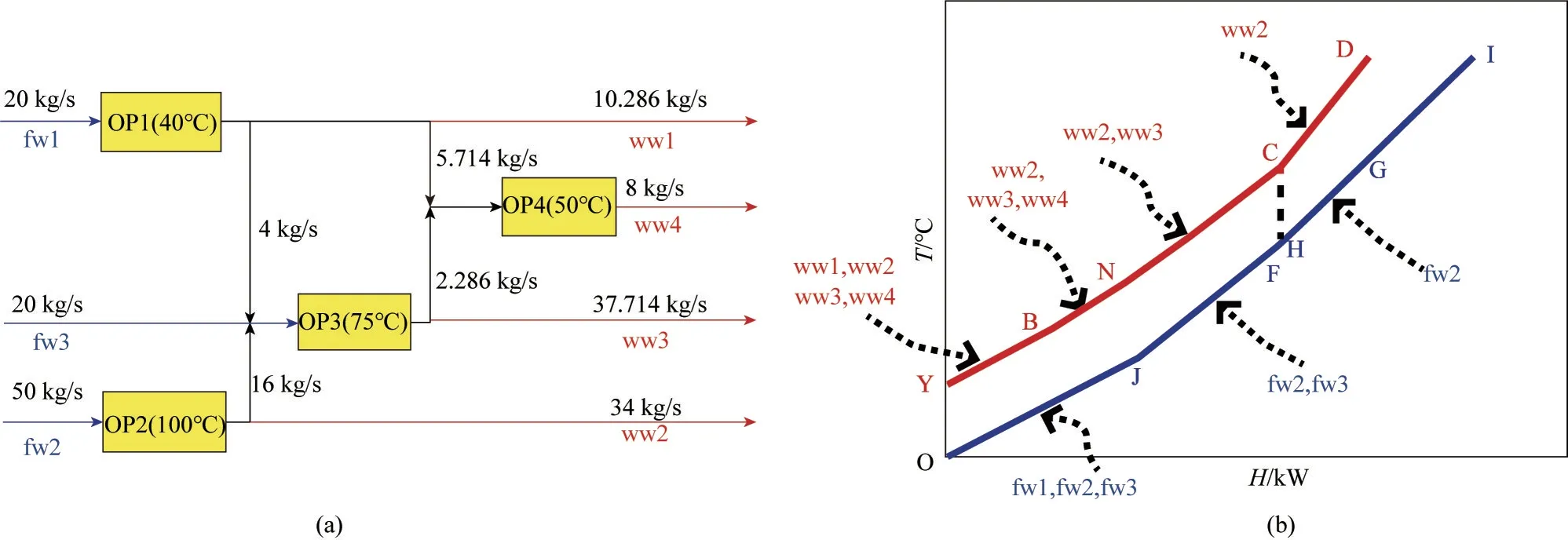
圖3 用水網絡結構與組合曲線對照圖Fig.3 Match of the water network and the energy composite curves

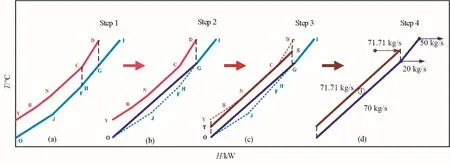
圖4 換熱匹配數為1的組合曲線演化過程Fig.4 Modification of combination curve with 1 heat exchange matching

3 基于分離系統的換熱網絡演化設計

為了得到更簡單的換熱網絡，本文對組合曲線進行演化以減少換熱匹配的個數。本文依次設計了換熱匹配數逐個增加的換熱網絡，并比較了每個換熱網絡的總換熱面積的大小。首先嘗試設計換熱匹配數為1 的換熱網絡，組合曲線的具體演化步驟如圖4所示。

第一步：以夾點為分界，判斷演化后組合曲線的夾點的上、下方各自存在幾組換熱匹配。如果存在多夾點，則選擇斜率變化最大的熱組合曲線的夾點處開始演化。當熱匹配數為1時，夾點上、下方都各存在1組換熱匹配。

第二步：通過連接節點的方式完成冷組合曲線演化。為了滿足流量要求，演化后的冷組合曲線在原冷組合曲線的上方，因此冷組合曲線的演化通過連接節點即可完成，所以冷組合曲線演化的自由度相對較低，更容易確定演化結果。先演化冷組合曲線可以降低整體操作的復雜性，也方便預判傳熱溫差的大小。在圖4（b）中，將冷組合曲線的點O 和點

與圖4的演化過程相似，圖5換熱匹配數為2的演化過程如下所述：

第一步：如圖5（a）所示，以線段CH 為分界點對組合曲線開始演化，判斷出演化后組合曲線的夾點的上、下方各存在1組換熱匹配。

第二步：如圖5（b）所示，演化冷組合曲線，連接點O和點H。

第三步：如圖5（c）所示，演化熱組合曲線。將線段BN 向兩端延長，與y 軸相交于點Q，與CH 相交于點K，夾點下方的熱組合曲線演化成線段QK。G 相連，冷組合曲線演化成OGI。新演化出的冷組合曲線用深藍色線段表示,原始組合曲線與演化后的組合曲線圍成的區域代表了流股間的非等溫混合。

第三步：演化熱組合曲線。通常在熱組合曲線中選擇與演化后的冷組合曲線斜率最為接近的線段向兩端延長。在圖4（c）中，熱組合曲線中線段NC 的斜率與OG 最接近，所以將NC 向兩端延長至TS，用深紅色表示。組合曲線經過演化之后的換熱匹配為TS/OG，其傳熱溫差小于10℃，傳熱溫差的限制需要被松弛。

第四步：如圖4（d）所示，每一個換熱匹配被視作一個分離系統，計算每個分離系統中的流股流率，以及在溫度節點處需要分流或合并的流股流率。根據演化后組合曲線的橫縱坐標完成上述流率的計算。

演化后組合曲線的總換熱量為22007.7 kW，總換熱面積為6825.1 m2。由于傳熱溫差較小，該換熱網絡雖然只有2個換熱單元，但是總換熱面積較大。為了減小換熱面積，將換熱匹配數調整為2，新的演化過程如圖5所示。

第四步：如圖5（d）所示，根據換熱匹配流股的溫變與焓變計算每個分離系統中需要分流或合并的流股流率。

圖5（d）的組合曲線的總體換熱量為22007.7 kW，換熱面積為4420.0 m2，相較于圖4（d）的換熱網絡而言，其換熱單元的個數從2 個增加到3 個，換熱面積有所減小。為了進一步增大傳熱溫差，需要將換熱匹配數調整為3，具體演化步驟如圖6所示。

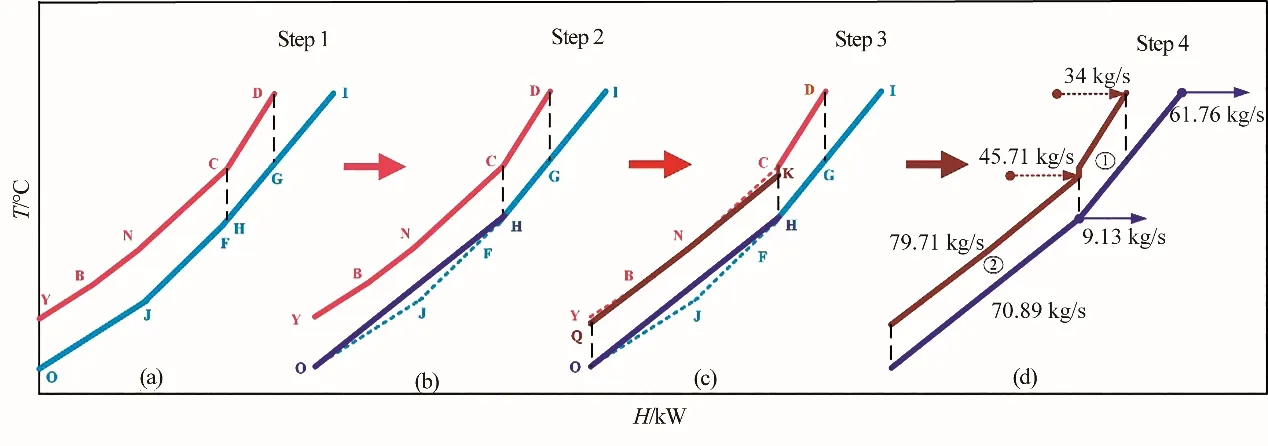
圖5 換熱匹配數為2的組合曲線演化過程Fig.5 Modification of combination curve with 2 heat exchange matching

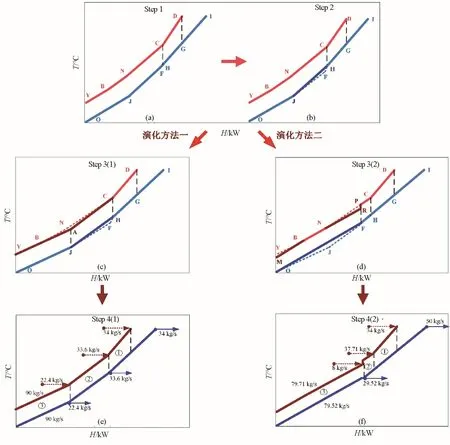
圖6 換熱匹配數為3的組合曲線演化過程Fig.6 Modification of combination curve with 3 heat exchange matching

在進行換熱匹配數為3 的組合曲線演化時，熱組合曲線有兩種演化方式，分別見圖6（c）與6（d），表2對比了演化一[圖6（e）]和演化二[圖6（f）]的換熱量與換熱面積大小。圖中標號為①、②、③的換熱匹配的換熱量為Q1、Q2、Q3，換熱面積為S1、S2、S3。

從表2可以看出，二者的總換熱量相等，但演化二的總換熱面積更大。在圖6(f)中，Q3具有較大的換熱量和較小的傳熱溫差，導致Q3大大增加了整體的換熱面積。所以為了演化出總換熱面積較小的網絡，對于傳熱溫差較小的換熱匹配，盡量分配較少的換熱量，反之亦然。圖6(e)為換熱匹配數為3時的最終演化結果，表3 為本案例3 個換熱匹配時本文與文獻的設計結果對比，文獻結果均采用本文的總傳熱系數重新計算。

表2 圖6（e）和圖6（f）的結果對比Table 2 Design comparison of Fig.6（e）and Fig.6（f）

表3 本文與文獻的設計結果對比Table 3 Overall design comparison

由表3 對比可知，在換熱器個數均為4 的情況下，本文與文獻結果的新鮮水量相同；本文的換熱量低于Leewongtanawit 等[35]的結果，所以總換熱面積較該文獻減小了1.3%。本文的換熱網絡采用串聯結構，所以總體換熱面積較Hong 等[43]的結果減小了4.8%。

為了繼續增大換熱匹配的傳熱溫差，本案例可以將換熱匹配數增加至4個，演化過程如圖7所示。

換熱匹配數為4 的換熱網絡總體換熱量為22007.7 kW，換熱面積為3596.3 m2。此換熱網絡的換熱單元數目為5個，但由于傳熱溫差較大，換熱面積相較上文有明顯減少。

本文就該案例分別設計了換熱匹配數為1、2、3、4 的換熱網絡，上述四個換熱網絡結構如圖8 所示，其換熱單元數目、換熱量與總換熱面積的對比見表4。

根據圖8 和表格4 的對比可知，上述四種演化方式所構建的換熱網絡中，總換熱量不發生變化，隨著換熱匹配個數的增加，傳熱溫差逐漸大，總換熱面積隨之減小。

本文總結了如下5個組合曲線演化步驟：

（1）判定演化后夾點上、下方的換熱匹配個數。

（2）演化冷組合曲線。冷組合曲線可以通過連接節點的方式完成演化。

（3）演化熱組合曲線。熱組合曲線要配合冷組合曲線進行演化，演化時要盡量保證換熱匹配的傳熱溫差足夠大。

（4）計算演化后每個換熱匹配中需要分流或合并的流股流率，并根據演化后的組合曲線構造換熱網絡。換熱網絡中流股的非等溫混合情況通過質量衡算和能量衡算來確定。

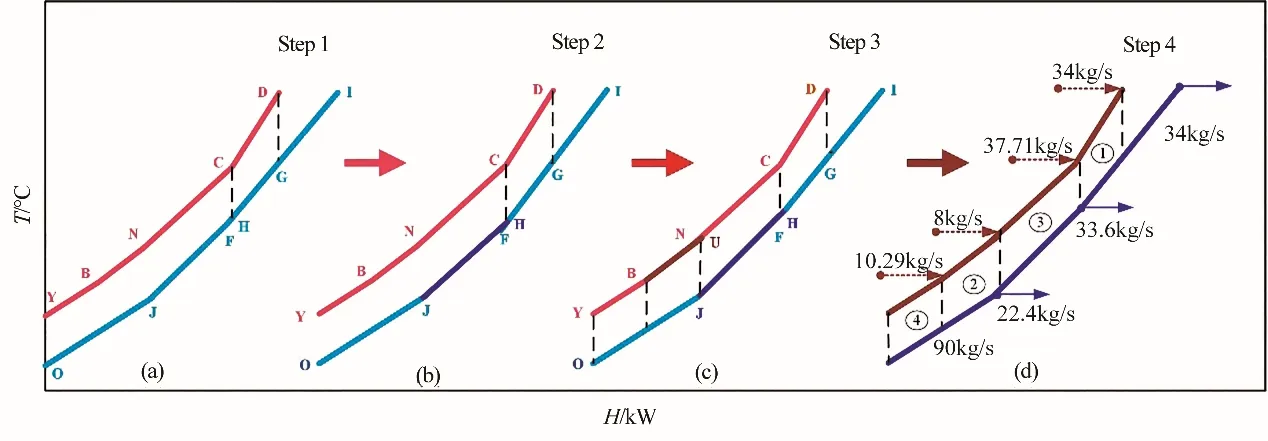
圖7 換熱匹配數為4的組合曲線演化過程Fig.7 Modification of combination curve with 4 heat exchange matching

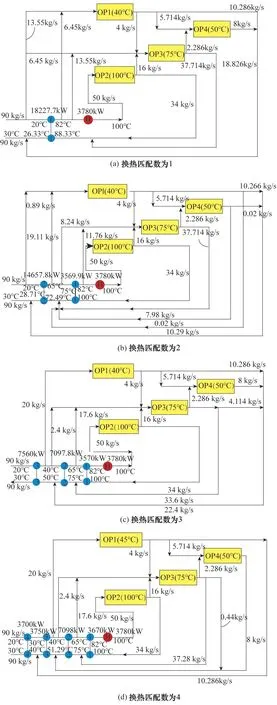
圖8 四種換熱網絡結構圖Fig.8 Heat exchanger networks with heat exchange matching of 1—4

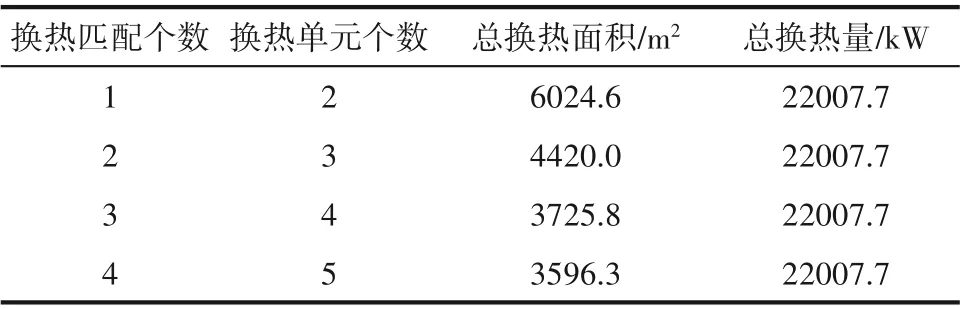
表4 四種換熱匹配的設計結果對比Table 4 Comparison of four design results

（5）換熱網絡設計完成之后判斷是否需要進一步演化，如果需要，則重復上述步驟。

另外，組合曲線的演化應遵循如下的5 個演化規則。

（1）保證演化后的組合曲線要在原本組合曲線的內部。即演化后的熱組合曲線要在原熱組合曲線的下方，演化后的冷組合曲線要在原冷組合曲線的上方。否則將沒有足夠流量的流股進行非等溫混合。

（2）如果組合曲線存在多個夾點，則在熱組合曲線上的夾點中，選擇斜率變化最大的夾點處開始演化。

（3）對于傳熱溫差較大的換熱匹配，盡量分配更多的換熱量；對于傳熱溫差較小的換熱匹配，盡量分配較少的換熱量。

（4）在演化熱組合曲線時，選擇熱組合曲線中與演化后的冷組合曲線斜率最為接近的線段，將該線段分別向兩端延長，作為熱組合曲線演化的重要參考。

（5）必要時要松弛對傳熱溫差的限制。如果演化后的組合曲線不能符合原本的傳熱溫差需求，則可以松弛對傳熱溫差的限制。

4 結 論

本文應用數學規劃法與概念設計法探究了熱集成用水網絡，得到了公用工程消耗量最小的情況下，換熱單元數更少、換熱面積更小的熱集成用水網絡結構。在用水網絡的設計中，本文構建了MINLP 模型，得到了公用工程消耗和總換熱面積最小條件下的用水網絡結構。其中總換熱面積通過冷熱組合曲線計算。在數學優化得到的用水網絡結構基礎上采用圖形方法設計換熱網絡。在分離系統中通過演化組合曲線以減少換熱匹配的個數，并且提出了減少換熱匹配的5 個步驟與5 項規則，該方法可以有效地減少換熱器數量。案例表明隨著換熱匹配數的增加，總換熱面積逐漸減小。其中換熱匹配數為3的結果優于文獻值。當流股數目較多時，換熱匹配結構較為復雜，本文中組合曲線演化的概念設計法不適用于大規模案例。

符 號 說 明

A——換熱器的總面積，m2

Fiw——用水單元i排放的廢水流率，kg/s

Fj,i——用水單元j 流向用水單元i 的回用水流率，kg/s

M——換熱網絡的年度總費用，$

QC——最小冷公用工程用量，kW

QH——最小熱公用工程用量，kW

QSIAp——候選夾點p上方的熱源，kW

QSOAp——候選夾點p上方的熱阱，kW

Qw——冷、熱流股間的換熱量，kW

SC——部分冷組合曲線與坐標軸圍成的面積，m2

SH——部分熱組合曲線與坐標軸圍成的面積，m2

SQ——陰影部分面積，m2

Th——從低到高排序后的熱流股初始溫度，℃

Ti,Tj——分別為用水單元i和j的操作溫度，℃

Tk——從低到高排序后的冷流股目標溫度，℃

Tp——候選夾點溫度，℃

θ——傳熱系數，kW/(m2·℃)

下角標

i——用水單元i

in——用水單元的入口

j——用水單元j

out——用水單元的出口