炸藥粉末壓制工藝參數(shù)對藥柱質(zhì)量的影響

曹 興，趙捍東，曹紅松，張程健，劉恒著，吳宗婭，熊瑞紅

(1.中北大學 機電工程學院，山西 太原 030051；2.山西江陽化工有限公司，山西 太原 030041)

引 言

聚能破甲戰(zhàn)斗部藥柱常采用粉末壓制成型工藝制備，該工藝將以HMX為基的塑料黏結(jié)炸藥通過模壓法在真空中壓裝成型[1]，藥柱成型密度、均勻性以及回彈量影響戰(zhàn)斗部的毀傷威力。為保證發(fā)射安全性及撞擊目標時的作用可靠性，成型藥柱必須保證密度的相對均勻。粉末壓制過程中，溫度、初始密度、壓制速率等工藝參數(shù)影響炸藥粉末壓制成型質(zhì)量，傳統(tǒng)炸藥粉末壓制工藝[2-3]通過檢測炸藥最終成型密度、回彈量來判斷藥柱質(zhì)量的好壞，借助實踐經(jīng)驗不斷調(diào)整工藝參數(shù)、改進壓制模具以及壓制方式，但這種方法成型后的炸藥粉末質(zhì)量難以保證。

目前，隨著計算機有限元技術(shù)的發(fā)展，金屬粉末壓制成型模擬已被用于工藝參數(shù)的優(yōu)化，而對于炸藥粉末壓制成型模擬也有學者進行了探索。張濤等[4]對高聚物黏結(jié)炸藥粉末溫壓成型過程進行了數(shù)值模擬,得到了成型壓力對高聚物黏結(jié)炸藥粉末成型的相關(guān)規(guī)律。劉群等[5]利用非線性有限元計算方法，對炸藥顆粒壓制成型過程進行了數(shù)值模擬計算，得出在一定壓力下，粉末壓制過程存在運動和變形兩個階段。以上均是研究壓制力工藝參數(shù)對炸藥粉末壓制成型的影響，而針對壓制速率以及初始密度對炸藥粉末壓制成型的影響未見報道。

本研究以聚能裝藥戰(zhàn)斗部為背景，利用高級非線性有限元軟件MSC.Marc建立JO-9159炸藥粉末藥柱壓制成型的連續(xù)體計算模型，模擬了炸藥粉末壓制成型過程，得到了壓制速率、初始密度對相對密度的影響規(guī)律以及在壓制過程中炸藥粉末位移變化規(guī)律。

1 有限元建模

目前，大多數(shù)學者針對粉末壓制成型過程的力學模型研究都是在基于連續(xù)體的假設(shè)上進行的，即將粉末材料視為體積可壓縮的彈塑性材料，整體上粉末材料遵循質(zhì)量不變條件，局部粉末顆粒遵循體積不變條件，本研究模擬炸藥粉末壓制成型過程也是將炸藥粉末視為連續(xù)體，運用彈塑性力學模型來分析炸藥粉末壓制過程的相關(guān)變化規(guī)律。采用更新拉格朗日方法求解炸藥粉末壓制過程，該過程屬于非線性問題，同時，在壓制過程中發(fā)生了大位移、大變形，而這種方法用于分析非彈性行為導致較大的變形，在分析中，初始拉格朗日坐標系幾乎沒有物理意義，因為非彈性變形是永久的。

1.1 炸藥粉末壓制工藝過程

稱取一定量的炸藥粉末，將其裝入模具中，給上模沖施加一定的外力，得到預定要求的炸藥高度、密度和一定炸藥強度的炸藥藥柱。圖1為炸藥粉末壓制模具示意圖。

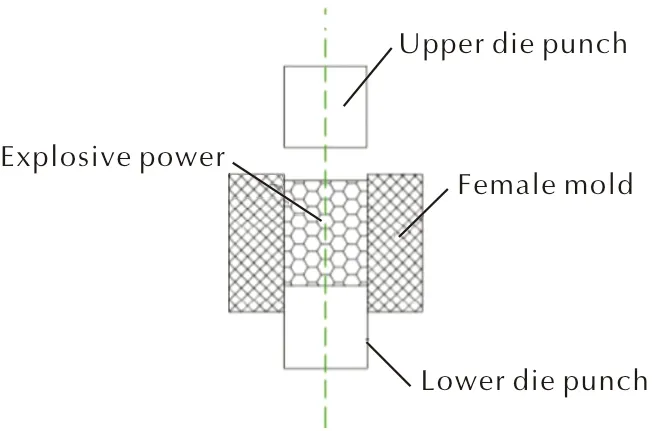
圖1 炸藥粉末壓制模具示意圖

1.2 有限元網(wǎng)格的初始劃分及重劃分設(shè)置

由于炸藥粉末壓制時所受的載荷是對稱的，同時炸藥幾何尺寸也是軸對稱的，為減小計算量，故簡化模型，以其軸線作為對稱軸，建立二維軸對稱有限元模型。對稱軸所在方向為X軸，徑向所在方向為Y軸，炸藥幾何尺寸為半徑13mm，粉末初始藥高44mm，設(shè)置初始相對密度為0.5，并劃分網(wǎng)格，設(shè)置網(wǎng)格單元尺寸為0.5，圖2為粉末壓制有限元模型。在模擬計算求解設(shè)置中，設(shè)置了網(wǎng)格重劃分準則，重劃分單元數(shù)量設(shè)置為10000網(wǎng)格。

圖2 JO-9159粉末壓制有限元網(wǎng)格計算模型

1.3 粉末材料本構(gòu)模型

粉末壓制屈服準則采用Shima-Oyane模型[6]。Shima和Oyane提出的粉末屈服準則在粉末成型有限元模擬中獲得廣泛應用，并被集成到MSC.Marc商業(yè)軟件中。屈服函數(shù)用于表達材料屈服所應滿足的函數(shù)關(guān)系，Shima-Oyane屈服函數(shù)分析粉末流動規(guī)律和相對密度分布規(guī)律，考慮粉末體在變形時的體積變化、流動應力和靜水壓力對粉末體屈服強度的影響。Shima-Oyane的修正模型數(shù)學表達式如下[7]：

(1)

式中：σy為單軸屈服應力；σd為偏應力分量張量；p為靜水壓力；γ、β為材料參數(shù)，為相對密度的函數(shù)，一般不為常數(shù)。需要通過材料試驗確定。由于γ、β不為常數(shù)，在實踐過程中，一般用如下公式表達：

γ=(q1+q2ρq3)q4

(2)

β=(b1+b2ρb3)b4

(3)

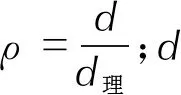
β=ρ5.5

(4)

γ=[6.25(1-ρ)]-0.5

(5)

該數(shù)據(jù)來源于Marc軟件手冊所提供的參數(shù)初始值，本研究q1、q2、q3、q4、b1、b2、b3和b4的值分別取0、1、1、5.5、6.25、-6.25、1和-0.5。

模擬采用的樣品為JO-9159炸藥，其密度為1.864g/cm3，屈服強度為30MPa。泊松比與相對密度關(guān)系表達式為μ=μ0×E-12.5(1-ρ)2[9],μ0表示致密炸藥的泊松比，取值為0.224，ρ為相對密度；彈性模量與相對密度的關(guān)系采用線性變化規(guī)律E=E0×ρ，E0為致密體的彈性模量，取值為8.4GPa。實際粉末壓制過程中，粉末與模具是有摩擦的，摩擦系數(shù)在有限元模擬中有著至關(guān)重要的作用，而影響摩擦系數(shù)的因素有很多，模具表面的光滑度、粉末的相關(guān)特性等，總體來說，摩擦系數(shù)是隨相對密度變化的，但文獻未有對摩擦系數(shù)的專門研究，因此，本研究不考慮摩擦對結(jié)果造成的影響，假設(shè)摩擦系數(shù)為定值0.2。

1.4 邊界條件及模擬設(shè)置

邊界條件定義了控制沖頭的運動狀態(tài)，添加控制點，利用控制點控制沖頭運動；設(shè)置初始條件，初始相對密度為0.5；模擬粉末壓制成型的實際過程共設(shè)置了加載工況、保壓工況以及卸載工況；收斂判據(jù)選擇殘余力或位移，收斂容差設(shè)置0.1。

2 壓制成型過程模擬及結(jié)果分析

在壓制速率0.2m/s時，分析炸藥粉末在壓制過程中位移、相對密度、回彈量以及模具的受力變化情況。

2.1 壓制過程中粉末位移變化規(guī)律分析

圖3為炸藥粉末總體位移變化云圖及軸向和徑向位移云圖。由圖3(a)可知，粉末壓制最終成型高度為21.72mm，壓制成型過程中，靠近上模沖的一側(cè)，炸藥粉末位移最大，且從上到下呈遞減的趨勢，呈階梯分布，其最大位移為22mm；在下模沖與炸藥粉末接觸的區(qū)域，炸藥粉末發(fā)生的位移最小，量級在10-2；在粉末壓制卸載過程中，炸藥位移有減小的趨勢，即發(fā)生了回彈，回彈量為0.28mm。

圖3 炸藥粉末總位移、軸向和徑向位移變化云圖

由圖3(b)和(c)可知，軸向發(fā)生的位移最大，徑向的位移最小，這表明粉末流動方向主要為軸向流動，揭示了粉末壓制成型的流動規(guī)律，這也驗證了張濤等[4]在PBX粉末成型的數(shù)值模擬研究中得到的結(jié)論：粉末壓制過程主要為軸向流動。

圖4為選取初始粉末不同軸向位置等間隔取點作為采樣點的示意圖。圖5為不同徑向位置在同一時間所對應的軸向位移。

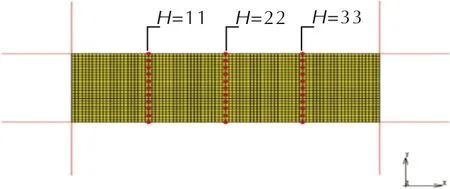
圖4 采樣點位置示意圖

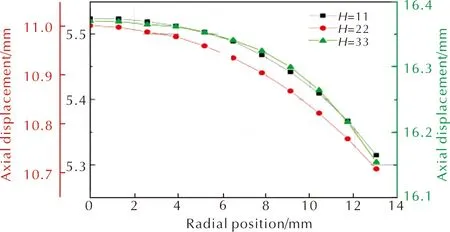
圖5 軸向位移隨徑向位置變化規(guī)律

由圖5可知，不同軸向位置，粉末徑向位置同一時間所對應的軸向位移具有相同的變化規(guī)律：炸藥粉末與模套接觸的側(cè)壁粉末位移較軸線處小，由此可以得出在炸藥粉末壓制成型過程中，靠近陰模的區(qū)域，炸藥粉末流動緩慢，在軸線區(qū)域，炸藥粉末流動較快，這是由于在陰模附近，炸藥粉末顆粒與陰模有較大的摩擦力,從而造成陰模附近粉末流動緩慢。

2.2 相對密度變化規(guī)律分析

粉末壓制成型后，相對密度變化云圖見圖6。從圖6可以看出，相對密度變化分布不均勻，平均值在0.97以上。進一步提取不同徑向位置處相對密度隨軸向位置變化數(shù)據(jù)，即Y值為0、6.5、13mm處的相對密度變化數(shù)據(jù)，如圖7所示，圖7(a)為提取的相對密度變化數(shù)據(jù)，圖7(b)為利用origin軟件對提取出的數(shù)據(jù)點進行擬合的樣條曲線。

圖6 相對密度變化云圖

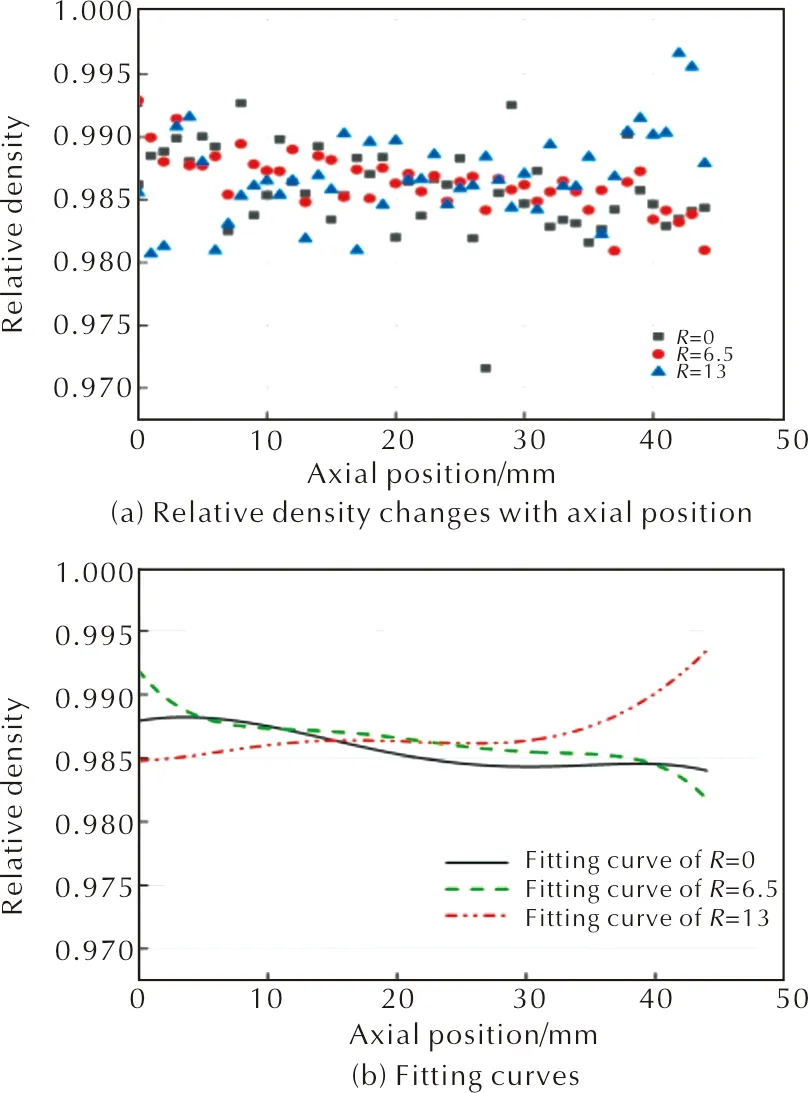
圖7 不同徑向相對密度隨軸向位置變化規(guī)律

從圖7中可以看出，靠近上、下模沖的區(qū)域炸藥粉末的相對密度較高，在中間區(qū)域，其相對密度數(shù)值較低，在0.982～0.990范圍之內(nèi)。總體來看，靠近陰模區(qū)域的相對密度值要大于其他區(qū)域的相對密度值。

利用工業(yè)CT檢測系統(tǒng)對成型藥柱進行切片檢測，結(jié)果見圖8。由圖8可知，炸藥粉末壓制成型后，不同區(qū)域密度分布有差異，但差異不明顯。通過對成型藥柱切成若干塊進行密度測試，其水平密度差約為0.3%，基本符合粉末壓制成型模擬結(jié)果，也證明粉末壓制成型采用Shima-Oyane模型是可行的，建模是成功的，模擬結(jié)果可以為炸藥粉末壓制工藝提供參考。

圖8 成型藥柱切片CT檢測圖

2.3 壓制過程陰模及模沖的受力影響分析

模沖與陰模受力大小影響模具的壽命，圖9為模具的受力曲線。

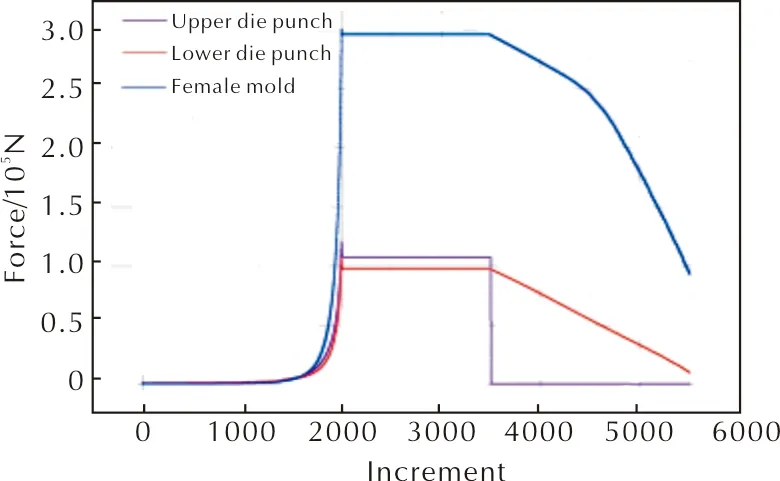
圖9 模具受力曲線

由圖9可知，在加載過程，上、下模沖以及陰模受力變化規(guī)律相同，呈指數(shù)分布，這是由于壓制初期，炸藥粉末處于松散狀態(tài)，到接近致密體時，炸藥粉末內(nèi)部阻力增大，為使其達到設(shè)定的高度，便需要較大的力推動，且陰模的受力大于上、下模沖的受力，其陰模最大受力為3.0×105N，上模沖最大受力為1.1×105N，下模沖最大受力為1.0×105N；在保壓過程，上、下模沖以及陰模所受到的力保持不變；在卸載過程中，上模沖的力瞬間減小，下模沖力的減小呈線性變化，對于陰模受力先緩慢減小，后期減小加快。因此，可以為模具的設(shè)計提供以下建議：由于陰模受到的作用力較大，上模沖次之，下模受到的力最小，因此，在制作模具時，陰模材料的選擇可以選擇強度高的材料，沖頭可以選擇強度較小的材料，這樣可以降低材料成本。

2.4 工藝參數(shù)對壓制成型藥柱質(zhì)量的影響

為了研究工藝參數(shù)對炸藥粉末壓制成型的影響，分析了不同壓制速率和初始相對密度對炸藥粉末壓制成型的影響。壓制速率選取210、220、230、240和250mm/s，初始相對密度選取0.6、0.7和0.8。

2.4.1 壓制速率對相對密度的影響

圖10和圖11分別為相對密度及其差值隨不同壓制速率的變化曲線。

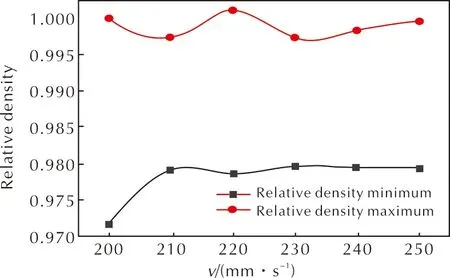
圖10 相對密度隨不同壓制速率的變化曲線

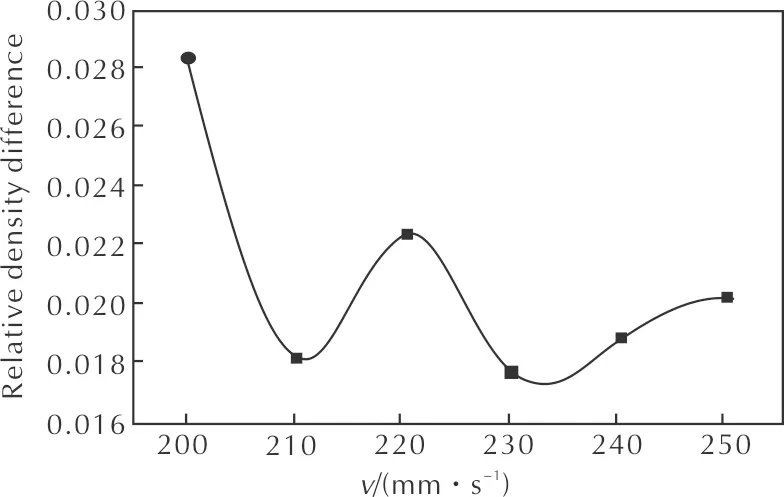
圖11 相對密度差值隨不同壓制速率的變化曲線

圖12為不同壓制速率下的相對密度分布云圖。分析不同壓制速率下相對密度變化情況發(fā)現(xiàn)，提高壓制速率有助于提高相對密度值，改善粉末致密性，且隨著壓制速率的提高，相對密度顯著提高，壓制速率提升到一定程度，相對密度值變化趨于平緩。分析圖12可知，隨著壓制速率的提高，粉末相對密度變得更加均勻。

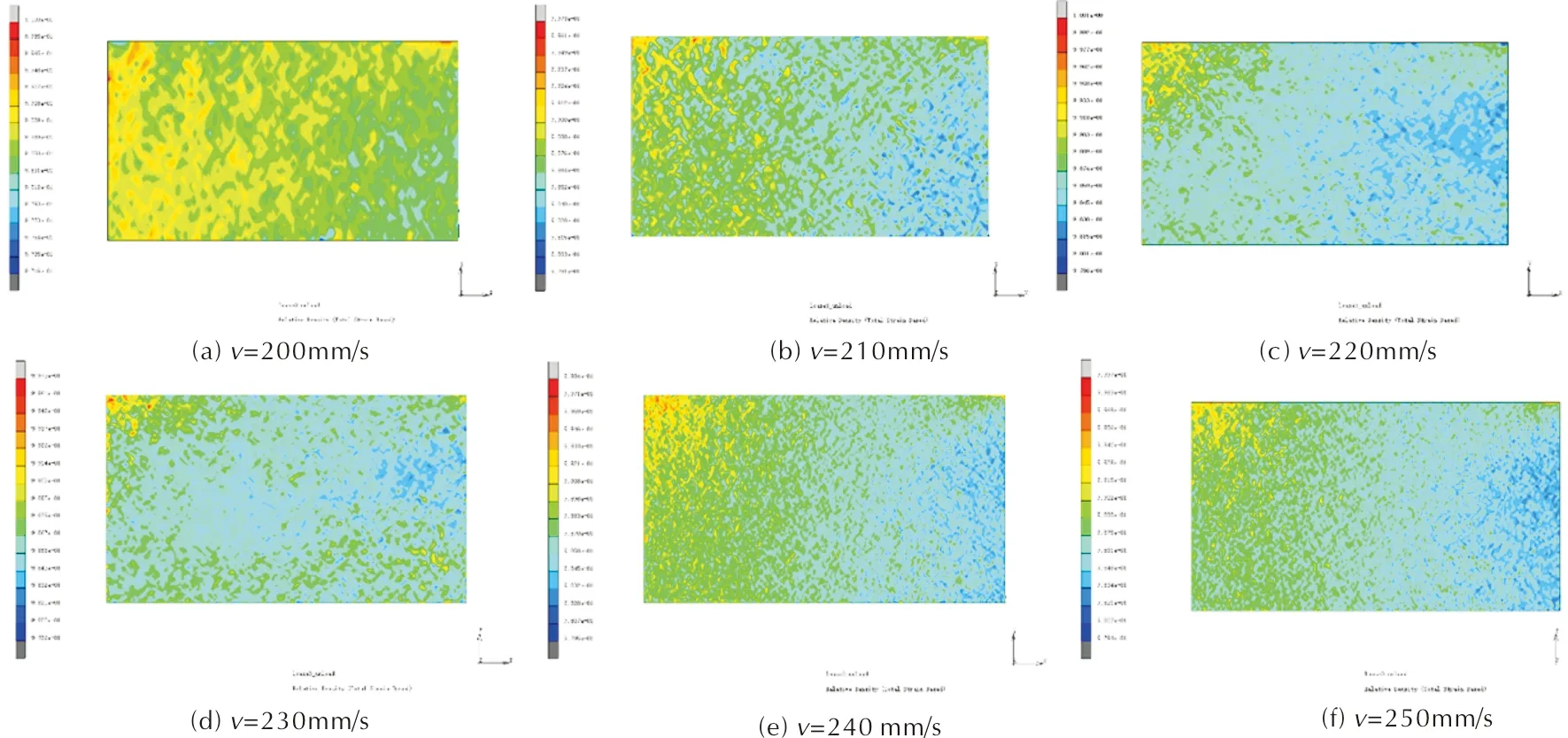
圖12 不同壓制速率相對密度變化云圖

2.4.2 壓制速率對回彈量的影響

回彈量影響炸藥藥柱的裝配以及炸藥的成型密度。繪制回彈量隨壓制速率變化曲線如圖13所示。由圖13可知，隨著壓制速率的增加，回彈量也在增加，最大值為0.3mm，最小值0.27mm。壓制速率在200～220mm/s內(nèi)，回彈量逐漸增加；壓制速率在220～230mm/s內(nèi)，回彈量趨于穩(wěn)定；壓制速率在230～240mm/s，回彈量又逐漸下降；壓制速率在240～250mm/s內(nèi)，回彈量又逐漸上升，且在壓制速率為240mm/s時，回彈量達到最小，為0.27mm。綜上所述，結(jié)合不同壓制速率對相對密度的影響，在所選壓制速率范圍內(nèi)，最優(yōu)的壓制速率為240mm/s。

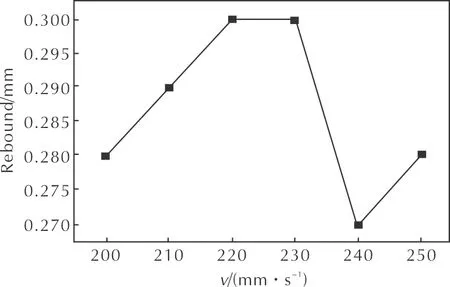
圖13 回彈量隨不同壓制速率的變化曲線

2.4.3 不同初始相對密度對相對密度的影響

圖14為相對密度隨不同初始相對密度變化曲線。分析曲線發(fā)現(xiàn),最大相對密度隨初始相對密度先增加后降低，最小相對密度隨初始相對密度先下降后上升。由此可見，初始相對密度在0.5～0.6時，粉末壓制效果最好。隨著初始相對密度的增加，等效米塞斯應力下降。增大初始相對密度，即增大松裝密度，有助于提升粉末壓制成型后的密度，降低等效米塞斯應力。

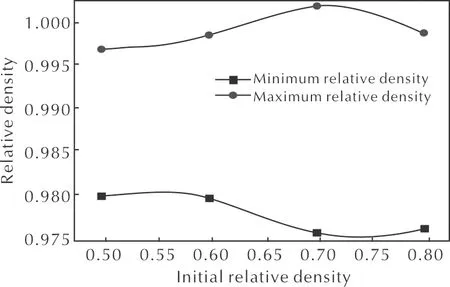
圖14 相對密度隨不同初始相對密度的變化曲線

3 結(jié) 論

(1)采用高級非線性有限元軟件MSc. Marc，借助Shima-Oyane粉末材料模型可以較好地模擬炸藥粉末壓制成型過程，粉末成型后密度分布情況與實際相符合。

(2)粉末壓制流動方向主要為豎向流動，且粉末與模具接觸區(qū)域流動較軸線處移動緩慢。粉末壓制成型后，粉末相對密度隨壓制速率呈非線性變化，在壓制速率為240mm/s時壓制效果最好。

(3)粉末壓制成型過程中存在回彈量。壓制速率為240mm/s時，粉末成型后回彈量最小。回彈量與壓制速率沒有固定的規(guī)律，整體上看，壓制速率大，回彈量較大。

(4)初始相對密度對粉末壓制成型有一定的影響，初始相對密度的提升有助于提高粉末成型后的相對密度。