橡膠減震器材料時變蠕變力學行為研究

馬 永，趙世平，盧丙舉，冷鼎鑫

(1.中國船舶集團有限公司第七一三研究所 河南 鄭州 450015；2.河南省水下智能裝備重點實驗室 河南 鄭州 450015；3.中國海洋大學 機械電子工程學院，山東 青島 266003)

0 引 言

橡膠減震器是發射裝置重要組成部分，布置在發射筒的周向環形空間，起到氣密、導向、適配、減震等作用。發射裝置減震器一般采用橡膠等材質，工作過程需要承受長時間預壓，間歇式瞬態大能量沖擊載荷作用。橡膠除了具有明顯的超彈性外，還具有蠕變等時間、溫度相關的粘彈性力學特性。橡膠長時間壓縮下力學性能的變化，影響減震器長期貯存使用壽命問題，以及發射過程的安全性。

蠕變研究的是材料“長期使用性能”，即形變、應力隨時間和溫度變化的現象與過程，是材料靜態粘彈性的基本表現。由于問題的復雜性和特殊性，工程一般多采用試驗方式分析橡膠減震器的蠕變性能[1-3]，但試驗往往有一定的離散性，且長時間蠕變試驗周期過長、成本大，很難得出規律性結論。在仿真應用方面，目前常采用Kelvin模型、Burgers模型和標準線性固體模型等線性機械模型描述材料的蠕變行為，但這些本構模型往往都有一定的局限性。近些年隨著非線性粘彈性材料的研究急劇增加，非線性粘彈性理論不斷得到完善，對非線性粘彈性本構模型的研究取得了大量的進展。Hanyga[4]、高慶等[5]研究了材料的多重積分型本構模型，但多重積分型本構方程由于應力、應變關系式過于復雜，本構模型參數不能從試驗中直接確定，難以在工程上推廣應用；冪律關系型本構關系函數數形式簡單、數值實現方便，在蠕變變形范圍小的工況中應用廣泛[6]；Bemstein，Kearsley 和 Zapas[7-8]依據Green-Rivlin，Coleman和Noll理論，詳盡地研究了有限變形的應力松弛問題，推導了不可壓縮固體和流體的非線性粘彈性本構關系，建立了BKZ理論；Christensen將非線性橡膠彈性理論擴展到了非線性粘彈性的情況，提出了一種適用于不可壓縮橡膠類材料的非線性粘彈性理論。Luo[9-12]根據工程學原理，引入損傷函數，在超彈性本構的基礎上，通過蠕變/松弛強度系數和蠕變/松弛軟化系數描述橡膠材料的蠕變特性。工程中實測獲得的工程對象隨時間的響應（如載荷、變形位移等）隱式地蘊含著材料的本構信息，即工程對象的應力-應變本構關系和模型參數，學者們應用不同系統識別模擬工具，針對本構模型選擇（模型辨識）及其參數確定等問題進行研究[13]。

本文開展減震器材料靜態力學以及48 h變載壓縮蠕變試驗，構建基于損傷函數的時變蠕變本構模型，利用abaqus/UHYPER用戶子程序接口對本構模型進行二次開發，完成本構模型參數識別。為更好地描述橡膠減震器蠕變損傷的力學特性，采用Von Mises屈服準則來評估橡膠材料的蠕變殘余變形，建立一種考慮永久變形的修正蠕變本構模型。

1 試驗研究

1.1 靜態力學試驗

靜態力學試驗的目的是獲取橡膠材料在單軸拉伸、等雙軸拉伸及平面拉伸變形下的應力-應變關系，并擬合得到相應的本構模型參數。

試驗設備包括電子萬能試驗機（型號WDW-10）、激光引伸儀（型號LE-05）裁刀、試樣基板、游標卡尺等。試驗溫度保持在常溫恒溫（23 ℃ ± 2°環境溫度）。試驗件與試驗過程、應力應變曲線，如圖1所示。

1.2 時變蠕變力學試驗

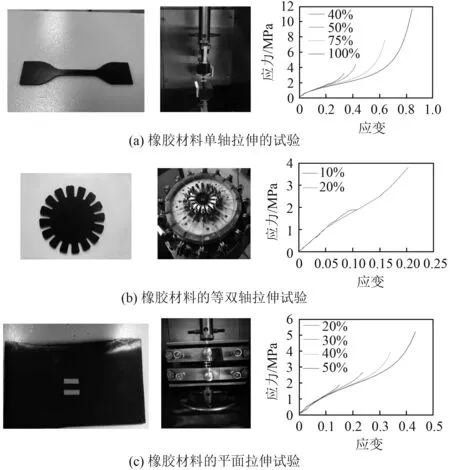
圖1 橡膠材料的靜態力學性能試驗Fig.1 Static mechanical properties test of rubber materials

時變蠕變力學試驗參考國家標準《GB19242-2003硫化橡膠在壓縮或剪切狀態下蠕變的測定》進行，試驗設備與橡膠材料靜態力學性能試驗設備相同。具體試驗流程為：將橡膠材料試樣放置于實驗機夾具正中心，調整試驗機，使夾具剛好與橡膠材料試樣接觸并且處于不受力狀態，調節壓縮試樣變形至中等變形，再返回原位，重復幾次，完成機械調節。機械調節的全過程在標準室內溫度下進行，機械調節在試驗之間間隔最長不超過48 h。機械調節結束后，開始正式試驗，在不超過15 s的時間內施加全力于試樣上，并且不明顯過量；達到滿負荷力之后，在不同的時間測定試樣的變形，這個力在整個試驗過程中保持恒定，力保載即48 h。橡膠材料的壓縮蠕變試驗外載荷分別取為1 000 N，1 500 N。對于橡膠材料，僅進行常溫壓縮蠕變試驗。在試驗過程中，記錄橡膠材料在不同加載條件下的蠕變試驗數據（時間、變形及載荷）。

橡膠試樣在不同加載水平下的蠕變試驗結果，如圖2所示。

由圖2可知，隨著時間的增加，橡膠材料的蠕變曲線斜率逐漸減小，表明橡膠的蠕變變形速率隨著時間的增加而逐漸變慢。

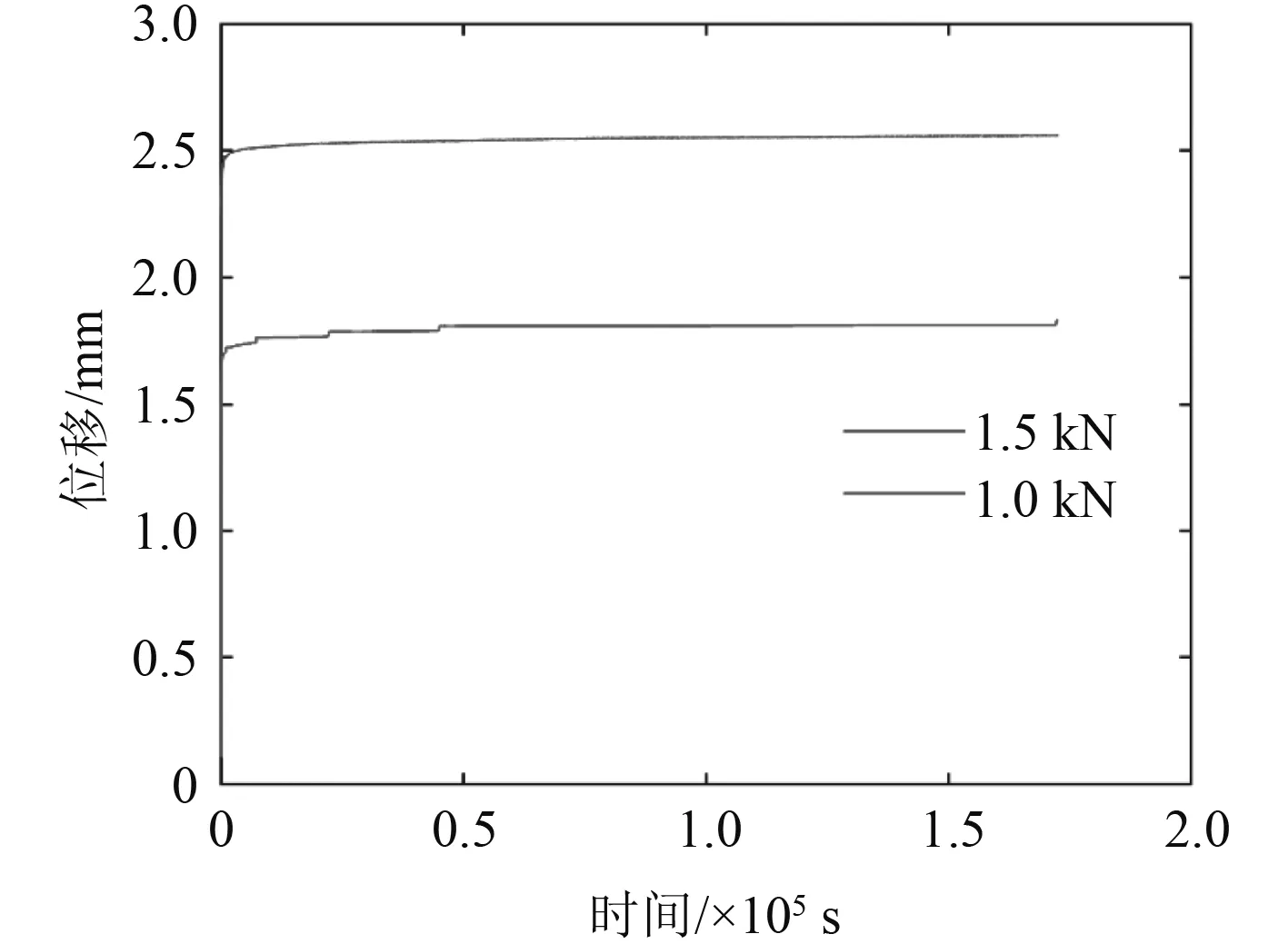
圖2 橡膠試件不同加載水平下蠕變試驗結果Fig.2 Creep test results of rubber specimens under different loading levels

2 材料本構模型及參數辨識

2.1 超彈性本構模型

橡膠材料的靜態力學特征可采用基于應變能函數的超彈本構模型來描述。基于應變不變量表示的連續介質唯象模型可寫成：

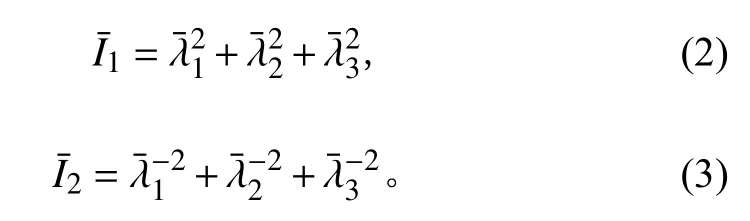
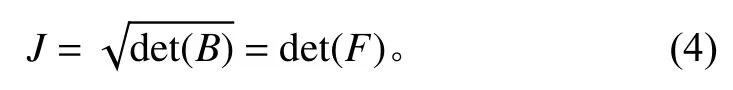
式中，F為變形梯度張量，計算如下式：

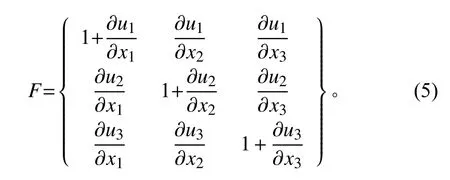
根據式（1）可推導出不同的超彈本構模型，其中多項式模型被廣泛應用于預測橡膠材料在外荷載激勵下的力學響應。多項式模型可寫為：

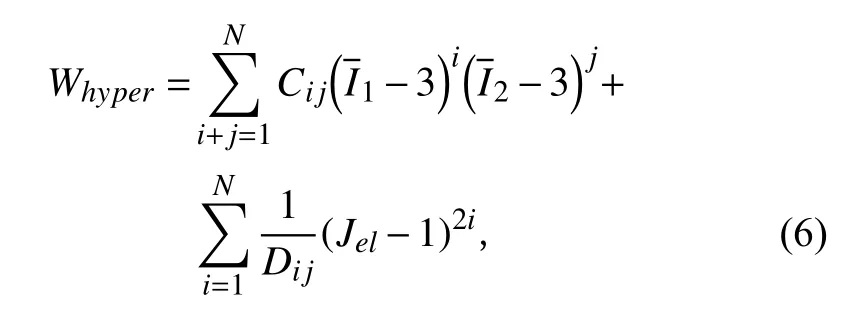
式中：Cij，Dij為橡膠材料的超彈系數，可通過橡膠的超彈力學試驗來確定。

對于式（6）取前兩項，則可得目前有限元計算中應用最廣泛的Mooney-Rivlin模型，其表達式為：

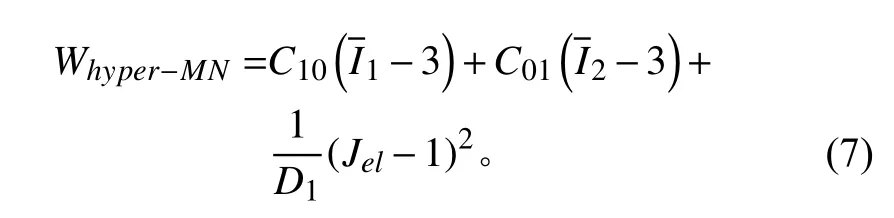
2.2 唯象蠕變本構模型

超彈本構模型可用于分析橡膠材料的靜力學特性，但其與時間效應無關，無法描述橡膠的粘彈性特性。為了評估橡膠材料在常量載荷作用下的蠕變效應，需對傳統超彈本構模型進行修正。引入帶有損傷意義的蠕變函數Wc-r，將橡膠材料的蠕變變形與時間相連，并假設蠕變變形與應變不變量，及時間歷程有關。由此，傳統的超彈性模型與時間歷程建立了聯系。修正后的唯象蠕變本構模型為：

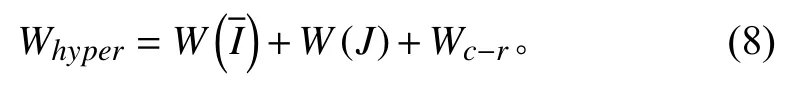
為描述時變損傷效應，構建冪函數形式的蠕變損傷函數，其具體表達式為[10-13]：

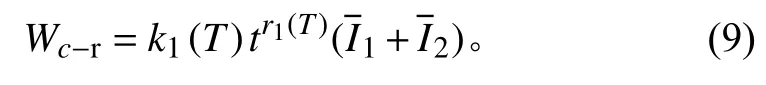
從數學角度考慮，式（8）為連續函數；從工程學方面考慮，式（9）提出的蠕變函數其參數均具有物理含義。其中T為荷載加載結束時刻的時間，k表征蠕變的損傷幅值，代表蠕變強度，r為衰減系數，描述了損傷隨時間衰減的程度。

2.3 本構模型參數識別

從本質上來說，式（8）提出的唯象蠕變本構模型是修正的超彈性本構模型，因此超彈性本構模型參數識別的準確度極為重要。根據最小二乘原理，利用橡膠材料的單軸拉伸、等雙軸拉伸、平面拉伸試驗數據，擬合得到本構模型參數。文獻[14]提出采用擬合優度R2來評估擬合誤差，其表達式為：

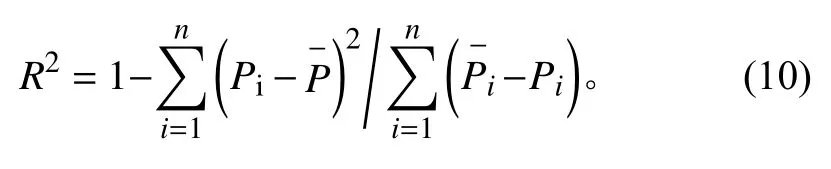
表1 橡膠材料超彈性本構模型參數Tab.1 Parameters of hyperelastic constitutive model for rubber materials

為進一步驗證模型參數的準確性，通過Abaqus有限元軟件，對橡膠材料的靜態力學特性進行數值模擬。根據試樣尺寸，建立橡膠試件的軸對稱幾何模型（Φ29 mm×12.5 mm），模型的上端與解析剛體相連，并在橡膠與剛體之間進行自由度耦合設置。采用CAX4HT單元對模型進行網格劃分，有限元模型如圖3所示。

圖3 橡膠試件有限元模型Fig.3 Finite element model of rubber specimen

將數值模擬的靜態壓縮特性與試驗結果進行對比，如圖4所示。

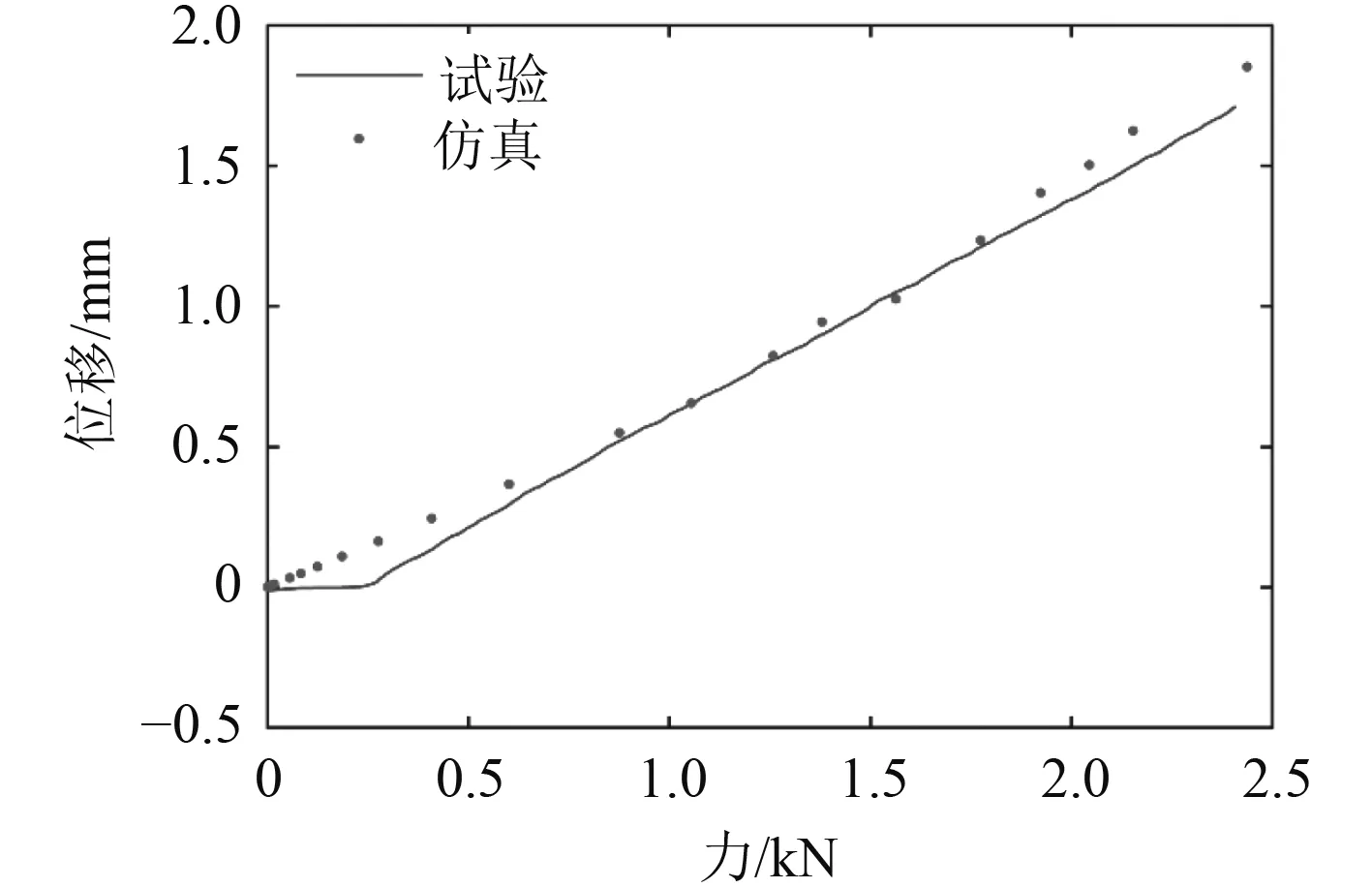
圖4 橡膠材料靜態壓縮試驗與仿真結果對比Fig.4 Comparison of static compression test and simulation results of rubber materials

由圖4可知，試驗與仿真結果吻合度較好，這說明超彈本構模型及參數選取合理，能夠表征橡膠在加載階段的非線性彈性特性，數值模擬精度良好。

基于式（10），利用Abaqus用戶自定義子程序UHYPER，將提出的蠕變本構模型通過Fortran語言進行編譯，并將編譯的子程序與有限元軟件進行關聯，開展橡膠材料的蠕變數值模擬。參照壓縮蠕變的試驗過程，仿真分析2種加載水平（1.0 kN和1.5 kN）下48 h的時變蠕變行為。

為明確蠕變本構參數對蠕變特性的影響程度，開展參數敏感性分析，敏感性范圍定為±20%。具體分析過程為：1）選擇一組蠕變參數作為參考參數，這里選取常溫1.5 kN作用下的橡膠蠕變參數（k0，r0）作為參考值；2）改變一個蠕變參數的數值并保持另一個蠕變參數數值不變，分析時變蠕變變形的變動范圍，如圖5所示。

不斷調整蠕變參數k和r，使仿真結果與試驗得出時間-蠕變變形誤差變小；分別對不同加載水平（1 000 N 和 1 500 N）的時間-蠕變變形試驗數據進行擬合，最終得出蠕變參數擬合結果（見表2）。

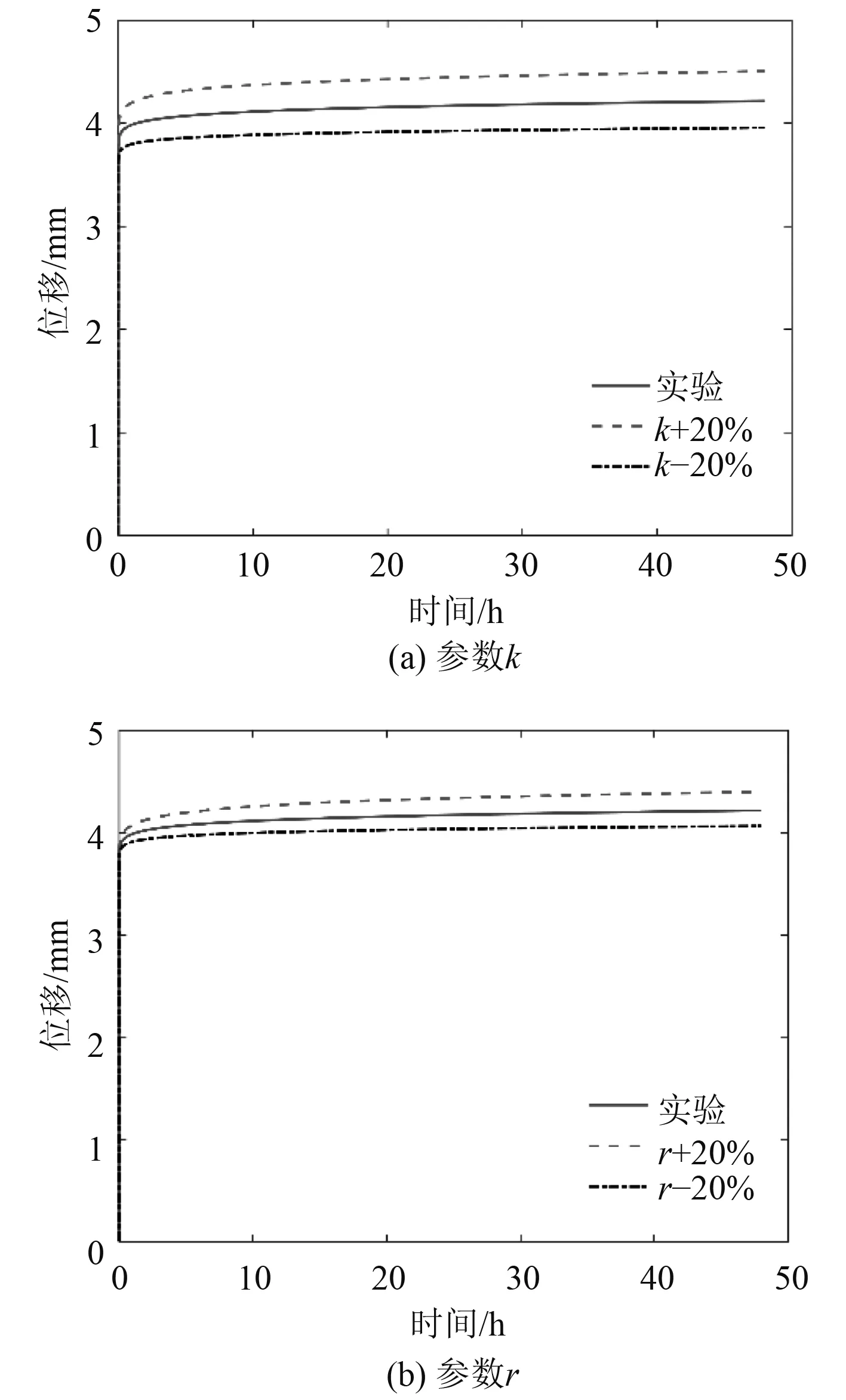
圖5 冪指數蠕變本構模型參數敏感性分析Fig.5 Parameter sensitivity analysis of power exponent creep constitutive model

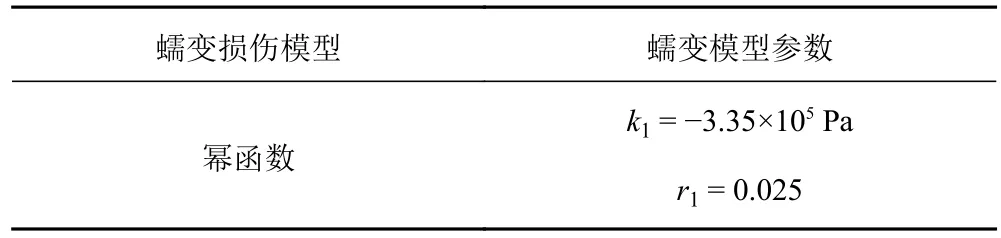
表2 橡膠蠕變參數擬合結果（23 ℃）Tab.2 Fitting results of rubber creep parameters（23 ℃）

為考察時變蠕變本構模型及參數的模擬精度，與橡膠試件不同載荷下的時間-蠕變變形進行對比。結果表明，試驗與仿真預測結果吻合度較好（見圖6）。

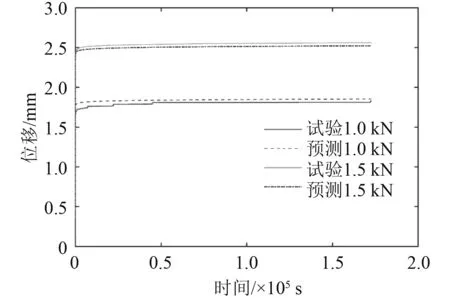
圖6 橡膠試件時間-變形仿真與試驗結果對比Fig.6 Comparison of time deformation simulation and experimental results of rubber specimen

為了詳細地說明時變蠕變變形規律，圖7對比了仿真得出的不同時刻橡膠材料的軸向蠕變變形。在蠕變過程中，橡膠材料的變形隨時間增加呈現非線性的變化特性。

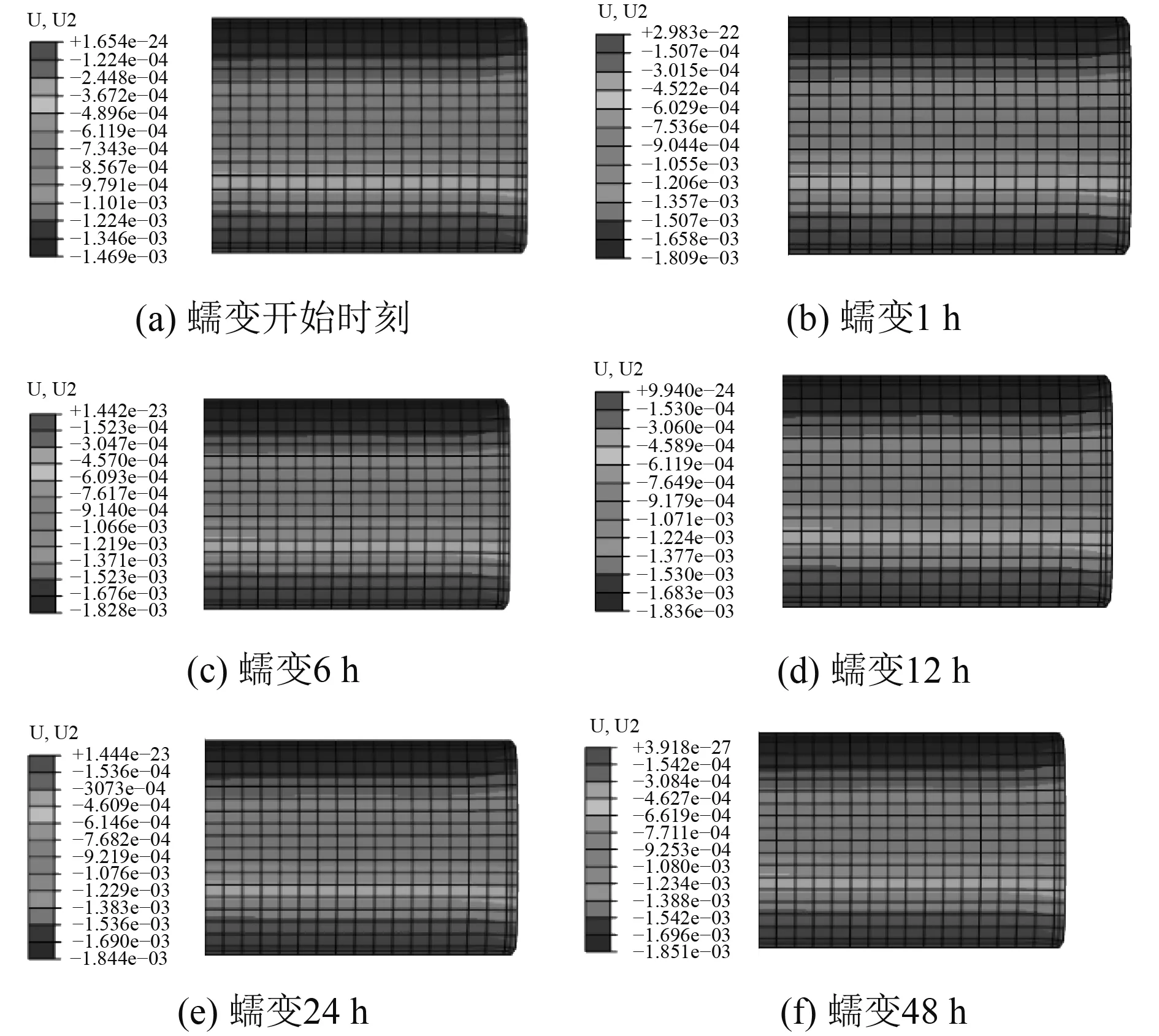
圖7 橡膠試件軸向蠕變變形分布Fig.7 Distribution of axial creep deformation of rubber specimens

由圖7可見，橡膠的軸向變形云圖呈現分層的現象：在材料底部，由于受到邊界條件的限制，變形量近似為0；在材料頂部，由于載荷條件的影響，變形量最大；而在其他區域，變形是逐漸變化的。這種蠕變變形的分層現象并未因蠕變時間的改變而發生變化。此外，材料的最大蠕變變形隨著時間的增加而增大，材料自由表面的膨脹效應也隨著時間的推移而愈發明顯。

在超彈性本構模型的基礎上引入蠕變損傷函數，構建的時變蠕變本構模型，很好描述了橡膠材料的壓縮蠕變性能。

3 減震器蠕變性能分析

圖8 橡膠減震器有限元模型Fig.8 Finite element model of rubber shock absorber

建立橡膠減震器的有限元模型，如圖8所示。模型上端與解析剛體相接觸，下端與剛性體連接，采用具有6個自由度的C3D8HT單元對模型進行網格劃分。載荷沿橡膠減震器垂直方向施加于上端解析剛體上，并通過剛體與橡膠器件之間的自由度耦合傳遞至器件。為了防止解析剛體與橡膠材料相互滲透，對接觸區域進行面與面接觸設置。

在橡膠減震器上表面加載2.1 t的載荷，橡膠減震器在在室溫條件下48 h蠕變過程中的應力分布云圖（見圖9）。

橡膠減震器在蠕變過程中的位移分布云圖，如圖10所示。

圖9 橡膠減震器在不同時刻的應力分布云圖Fig.9 Stress distribution nephogram of rubber shock absorber at different times

圖10 橡膠減震器在不同時刻的位移分布云圖Fig.10 Displacement distribution nephogram of rubber shock absorber at different times

由圖9和圖10可知，在蠕變過程中橡膠減震器的應力最大值始終出現在器件的外側位置；橡膠器件與材料的分布云圖相似，均出現了分層現象，但器件的分層變形不如材料的明顯，這是由于器件結構效應引起的。隨著蠕變時間的增加，減震器的蠕變變形也在不斷增加，橡膠減震器蠕變行為的時間-蠕變變形曲線如圖11所示。

圖11 橡膠減震器時間-蠕變變形曲線Fig.11 Time creep deformation curve of rubber shock absorber

由圖11可知，橡膠減震器在15 s時的蠕變變形為5.43 mm，48 h 后蠕變變形達到 5.97 mm，在整個時變過程中，蠕變變形較為平緩。

為了描述橡膠減震器在蠕變條件下的損傷永久變形，我們對時變蠕變本構模型進行進一步擴展，采用Von Mises屈服準則來評估橡膠材料的蠕變殘余變形，提出一種考慮永久變形的修正蠕變本構模型，其表達式為：

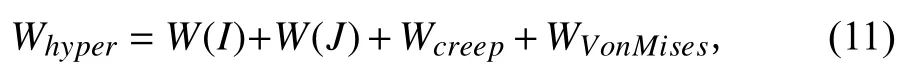
式中，基于屈服準則的分段本構方程為：

式中： σy0， σy1， σy2為第1，2，3階屈服應力； εy0，εy1， εy2為各屈服應力對應的應變；為硬化系數；KP是長期模量。

橡膠器件蠕變前后的剛度變化，如圖12所示。

由圖12可知，當位移為5 mm時，減震器未蠕變前的承載為17 045.4 N，引入蠕變損傷后的器件承載力為13 430.2 N，降低了21.2%。定義等效剛度為：

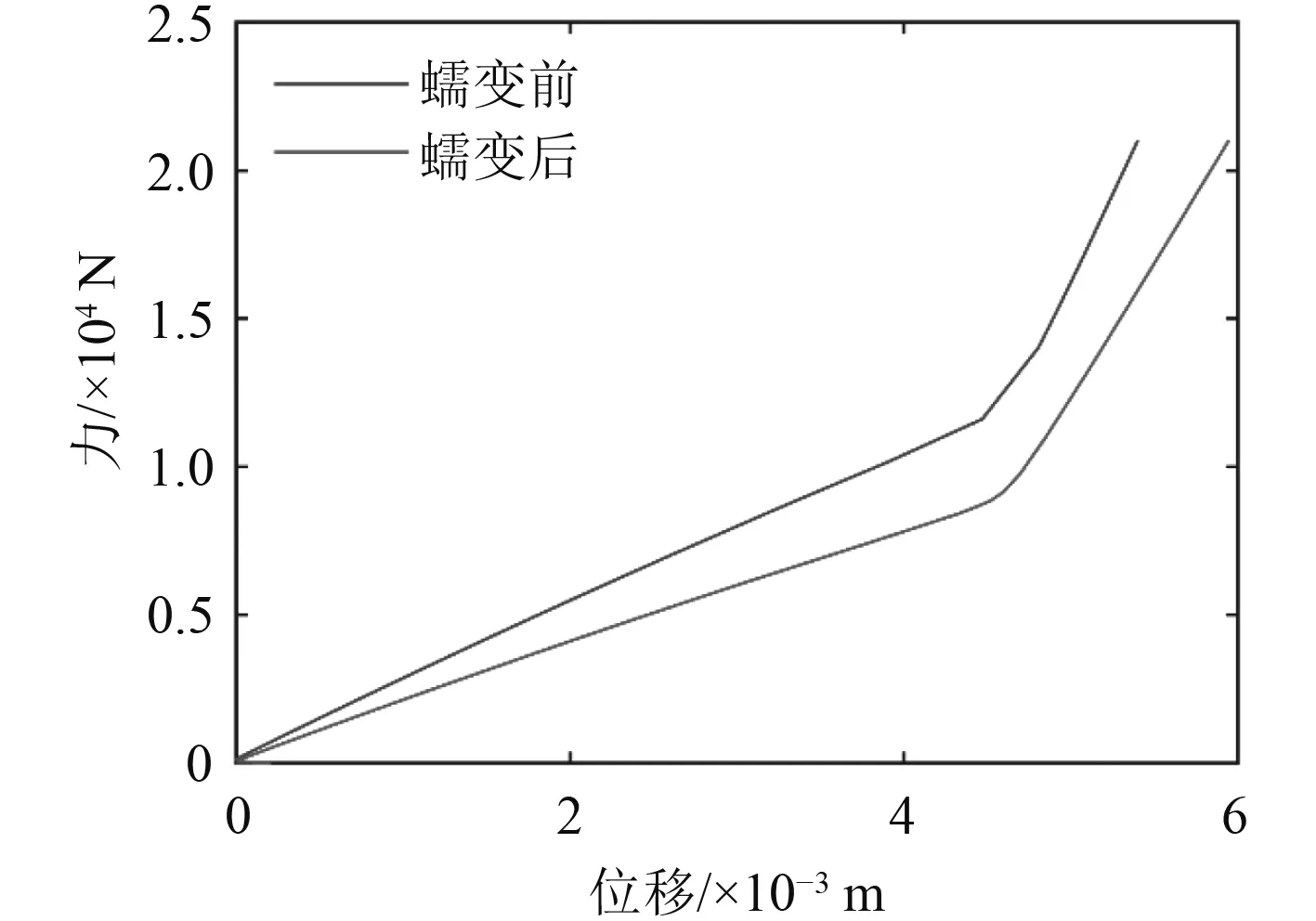
圖12 橡膠器件蠕變前后剛度對比Fig.12 Comparison of stiffness of rubber components before and after creep

其中， ΔF為載荷變化量， Δx為位移變化量。由圖12可知，橡膠器件在蠕變前與蠕變后的等效剛度分別為3.89×106N/m 和 3.53E6 N/m，退化了 9.1%。

橡膠減震器蠕變前與損傷蠕變后靜態變形不同位移處的應力分布云圖，如圖13所示。

圖13 蠕變前后不同位移處應力分布云圖Fig.13 Nephogram of stress distribution at different displacements before and after creep

由圖13可知，減震器在考慮蠕變損傷效應后，其靜態變形的最大應力呈現退化趨勢。當靜態位移為1 mm時，蠕變前與蠕變后的應力最大值分別為0.41 MPa和0.17 MPa；當位移為3 mm時，蠕變前/后的應力最大值分別為 1.10 MPa 和 0.67 MPa；當位移為 5 mm 時，蠕變前/后的應力最大值分別為 1.80 MPa 和 1.33 MPa。

4 結 語

本文開展了減震器橡膠材料在 1 000 N 和 1 500 N兩種載荷水平下48 h蠕變試驗研究，通過對蠕變試驗數據分析，可以得出以下結論：

1）在超彈性本構模型的基礎上，引入損傷意義的蠕變函數，將荷載引起的橡膠材料的蠕變與時間相連，構建了時變蠕變本構模型；采用Von Mises屈服準則來評估橡膠材料的蠕變殘余變形，提出一種考慮永久變形的修正蠕變本構模型。

2）通過Abaqus/UPYPER用戶子程序，將橡膠材料的時變蠕變本構模型用Fortran語言編譯，構建了橡膠材料及減震器蠕變性能仿真分析模型。

3）對不同載荷水平下的橡膠材料的蠕變試驗曲線對比，仿真與實驗結果吻合度較好，說明時變蠕變本構模型很好的描述了橡膠材料的蠕變性能，且預測精度滿足工程應用。

4）通過橡膠減震器48 h壓縮蠕變試驗與仿真結果對比，驗證了方法的可行性。