基于模型補(bǔ)償自抗擾的彈體滾轉(zhuǎn)角控制策略

吳正平，鄧 聰

(三峽大學(xué)電氣與新能源學(xué)院，湖北 宜昌 443002)

0 引言

干擾彈在作戰(zhàn)過(guò)程中，需要調(diào)整彈體的滾轉(zhuǎn)角去對(duì)準(zhǔn)敵方武器并發(fā)出干擾信號(hào)，起到干擾作戰(zhàn)的功能[1]。彈體滾轉(zhuǎn)通道的穩(wěn)定性與迅速調(diào)整滾轉(zhuǎn)角的能力是能夠?qū)崿F(xiàn)干擾彈精確對(duì)準(zhǔn)、穩(wěn)定飛行控制的關(guān)鍵；但干擾彈現(xiàn)在所處的作戰(zhàn)環(huán)境也日益復(fù)雜，在飛行過(guò)程中，會(huì)受到各種各樣的干擾例如氣動(dòng)摩擦產(chǎn)生的干擾力矩、電機(jī)軸承間的干擾等等。這些干擾力矩的存在，增加了彈體滾轉(zhuǎn)角控制的難度[2]。

文獻(xiàn)[3]提出了基于魯棒控制的策略，文獻(xiàn)[4]提出了雙閉環(huán)控制策略，文獻(xiàn)[5]提出了基于變結(jié)構(gòu)控制的策略，雖然在理想的仿真環(huán)境下可以達(dá)到很好的控制效果，但在實(shí)際控制系統(tǒng)中，由于模型建立不精確以及未知擾動(dòng)的存在，在實(shí)際運(yùn)用中的效果難以保證。文獻(xiàn)[6]提出基于線性二次型調(diào)節(jié)器的滾轉(zhuǎn)控制方法，在擾動(dòng)變化較大時(shí)會(huì)影響觀測(cè)器的精度，抗擾性不強(qiáng)，進(jìn)而導(dǎo)致控制精度降低。文獻(xiàn)[7]提出了一種基于模糊控制的滾轉(zhuǎn)角控制策略，對(duì)控制器的參數(shù)進(jìn)行在線調(diào)整，但隨著精度要求越高，模糊控制器的決策就越慢，有可能會(huì)導(dǎo)致無(wú)法實(shí)時(shí)控制的情況。

本文針對(duì)傳統(tǒng)控制策略存在的不足，提出了基于模型補(bǔ)償自抗擾的彈體滾轉(zhuǎn)角控制策略，通過(guò)對(duì)彈體滾轉(zhuǎn)角控制系統(tǒng)進(jìn)行數(shù)學(xué)建模，建立擴(kuò)張狀態(tài)觀測(cè)器，再將擴(kuò)張狀態(tài)觀測(cè)器的觀測(cè)量作為模型已知信息，增加到干擾補(bǔ)償中，并分析了該控制策略的穩(wěn)定性。

1 數(shù)學(xué)模型

1.1 彈體滾轉(zhuǎn)通道數(shù)學(xué)模型

本文的實(shí)驗(yàn)對(duì)象彈體滾轉(zhuǎn)通道控制系統(tǒng)核心部件為反作用飛輪、滾轉(zhuǎn)本體(彈體)、旋轉(zhuǎn)翼等。反作用飛輪由伺服電機(jī)、伺服驅(qū)動(dòng)器、角度檢測(cè)電路、反作用飛輪輪體等組成。

對(duì)彈體滾轉(zhuǎn)通道由角動(dòng)量守恒定理可得：

(1)

式(1)中，Jb為滾轉(zhuǎn)本體的轉(zhuǎn)動(dòng)慣量，a為摩擦系數(shù)，θ為滾轉(zhuǎn)角，Jw為反作用飛輪的轉(zhuǎn)動(dòng)慣量，Ω為反作用飛輪角速度，Md為干擾力矩。

滾轉(zhuǎn)角串級(jí)控制系統(tǒng)結(jié)構(gòu)框圖如圖1所示，其中θ0和θ分別是期望的滾轉(zhuǎn)角與實(shí)際的滾轉(zhuǎn)角，Tf1和Tf2都是干擾力矩。內(nèi)環(huán)控制采用PD控制，達(dá)到快速控制的目的，外環(huán)使用模型補(bǔ)償自抗擾控制策略以滿足系統(tǒng)抗擾性、精確度的要求。

圖1 滾轉(zhuǎn)角串級(jí)控制系統(tǒng)結(jié)構(gòu)框圖Fig.1 Structure diagram of roll angle cascade control system

1.2 擴(kuò)張狀態(tài)空間表達(dá)式的建立

(2)

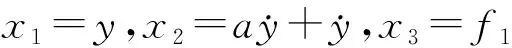
(3)

(4)

由此，建立了以反作用飛輪角加速度為控制量輸入，彈體滾轉(zhuǎn)角為輸出的系統(tǒng)擴(kuò)張狀態(tài)空間表達(dá)式。下面根據(jù)以上系統(tǒng)，進(jìn)行控制策略設(shè)計(jì)。

2 基于模型補(bǔ)償自抗擾的彈體滾轉(zhuǎn)角控制策略

傳統(tǒng)形式的自抗擾控制器設(shè)計(jì)，對(duì)系統(tǒng)數(shù)學(xué)模型并無(wú)過(guò)多的借鑒，只需知道系統(tǒng)的階數(shù)，進(jìn)而設(shè)計(jì)高于系統(tǒng)一階的擴(kuò)張狀態(tài)觀測(cè)器[8]。要想達(dá)到良好的控制效果，其中z3對(duì)總干擾f的準(zhǔn)確估計(jì)是很重要的。傳統(tǒng)自抗擾控制中，當(dāng)干擾出現(xiàn)劇烈的變化時(shí)，對(duì)擴(kuò)張狀態(tài)觀測(cè)器來(lái)說(shuō)是一個(gè)很大的挑戰(zhàn)，很可能精度降低甚至難以跟蹤。

2.1 滾轉(zhuǎn)角控制系統(tǒng)的模型補(bǔ)償自抗擾控制策略

由第一章中建立的數(shù)學(xué)模型可知，本系統(tǒng)的部分模型已知，可以補(bǔ)償?shù)綌U(kuò)張狀態(tài)觀測(cè)器中來(lái)增加觀測(cè)器的穩(wěn)定性。

由式(3)和式(4)建立模型補(bǔ)償?shù)臄U(kuò)張狀態(tài)觀測(cè)器如下：

(5)

下面先進(jìn)行觀測(cè)器的極點(diǎn)配置，將其極點(diǎn)配置在-ω0。

(6)

由式(6)即可得：l1=a+3ω0，l2=(3a+3)ω02+(3a2+3a)ω0+a3+a2，l3=ω03。

最后，基于模型補(bǔ)償?shù)娜A擴(kuò)張狀態(tài)觀測(cè)器形式如下：

(7)

式(7)中，z1是對(duì)滾轉(zhuǎn)角的觀測(cè)，z2是對(duì)(a+1)倍的滾轉(zhuǎn)角速度的觀測(cè)，z3是對(duì)干擾f1的觀測(cè)。若能夠準(zhǔn)確實(shí)現(xiàn)對(duì)每個(gè)狀態(tài)的觀測(cè)，設(shè)計(jì)如下控制器:

(8)

(9)

此時(shí)z3≈f+(b-b0)-az2，與傳統(tǒng)自抗擾控制相比，z3需要跟蹤的干擾量大大減小，跟蹤精度也會(huì)有所提升。

彈體滾轉(zhuǎn)角外環(huán)模型補(bǔ)償自抗擾控制系統(tǒng)結(jié)構(gòu)框圖如圖2所示。

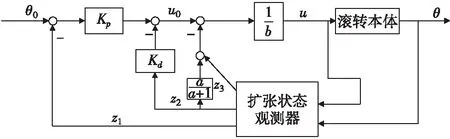
圖2 彈體滾轉(zhuǎn)角外環(huán)自抗擾控制系統(tǒng)結(jié)構(gòu)框圖Fig. 2 Structural diagram of auto disturbance rejection control system for outer ring of rolling angle of projectile

2.2 收斂性與跟蹤誤差分析

由式(7)可求得z1、z2、z3的傳遞函數(shù)如下：

(10)

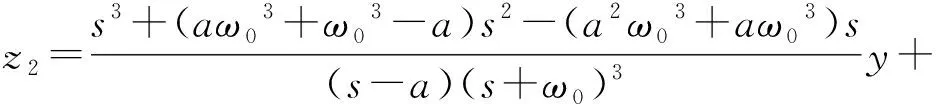
(11)

(12)

(13)

(14)

(15)

考慮到分析典型性,y、u均取幅值為K的階躍信號(hào)y(s) =K/s,u(s) =K/s, 則可以求得穩(wěn)態(tài)誤差：

(16)

由式(16)可知，所設(shè)計(jì)的模型補(bǔ)償自抗擾控制策略具有很好的收斂性與跟蹤性能，能夠?qū)崿F(xiàn)對(duì)系統(tǒng)狀態(tài)變量和擾動(dòng)的無(wú)差估計(jì)。

3 仿真與實(shí)驗(yàn)分析

3.1 Simulink仿真

為便于分析，由式(1)建立的數(shù)學(xué)模型在Simulink環(huán)境下搭建彈體滾轉(zhuǎn)角控制系統(tǒng)。系統(tǒng)所取參數(shù)為：反作用飛輪的轉(zhuǎn)動(dòng)慣量Jw=0.078 kg·m2，滾轉(zhuǎn)本體的轉(zhuǎn)動(dòng)慣量Jb=0.026 kg·m2，摩擦系數(shù)a=0.8。自抗擾控制器參數(shù)選取為：觀測(cè)器極點(diǎn)ω0=-10，控制器極點(diǎn)ωc=-8。在設(shè)定1 s時(shí)進(jìn)行階躍輸入，2 s時(shí)有階躍干擾，有如圖3—圖5的仿真圖。

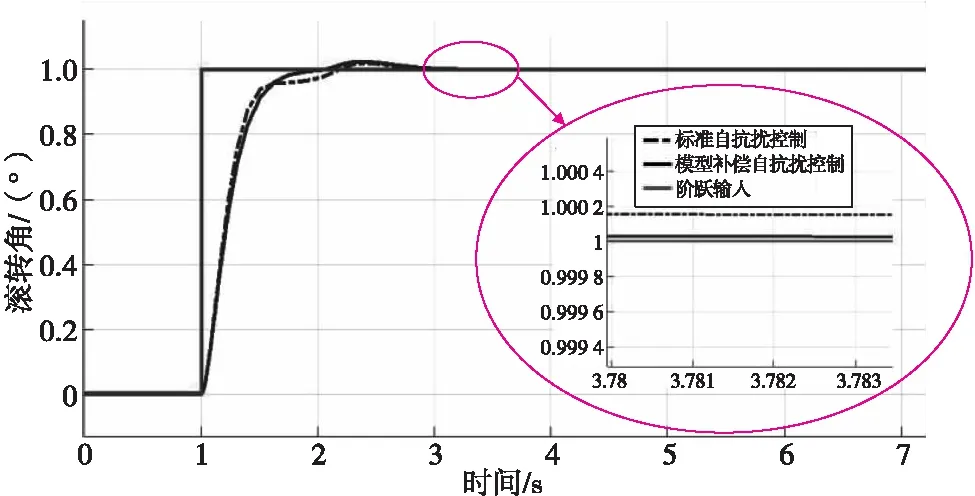
圖3 階躍輸入響應(yīng)圖Fig.3 Step input response diagram

由階躍輸入響應(yīng)圖3可知，模型補(bǔ)償自抗擾控制調(diào)節(jié)時(shí)間明顯比傳統(tǒng)自抗擾控制時(shí)間短，調(diào)節(jié)的精度也比傳統(tǒng)自抗擾控制高。

圖4是z1、z2跟蹤效果對(duì)比圖，由z1對(duì)滾轉(zhuǎn)角跟蹤圖4(a)、(b)可知，傳統(tǒng)自抗擾控制與模型補(bǔ)償自抗擾控制都可以很好實(shí)現(xiàn)對(duì)滾轉(zhuǎn)角的跟蹤。

由z2跟蹤圖4(c)、(d)可知，z2(模型補(bǔ)償自抗擾控制)對(duì)(a+1)倍滾轉(zhuǎn)角速度的跟蹤存在的誤差比z2(傳統(tǒng)自抗擾控制)對(duì)滾轉(zhuǎn)角速度的跟蹤誤差要小。

圖4 z1、z2跟蹤效果對(duì)比Fig.4 Comparison of tracking effect between z1 and z2

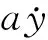
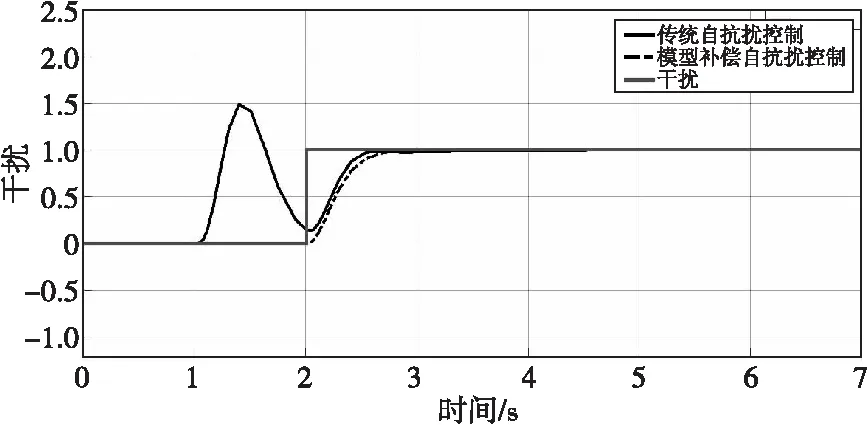
圖5 z3(對(duì)干擾的跟蹤)Fig.5 z3 (tracking interference)

3.2 彈體滾轉(zhuǎn)控制系統(tǒng)實(shí)驗(yàn)

搭建如圖6所示系統(tǒng)實(shí)物圖，圖6中1是旋轉(zhuǎn)翼與反作用飛輪相連接，可增大其轉(zhuǎn)動(dòng)慣量，2用來(lái)配置轉(zhuǎn)動(dòng)慣量，與實(shí)際被控對(duì)象的轉(zhuǎn)動(dòng)慣量一致。進(jìn)行了連續(xù)50°階躍輸入實(shí)驗(yàn)。圖7是狀態(tài)曲線圖，圖8是系統(tǒng)響應(yīng)曲線圖。由圖可見(jiàn)基于模型補(bǔ)償?shù)淖钥箶_控制可以達(dá)到對(duì)彈體滾轉(zhuǎn)角控制的精度、抗擾性的要求。

圖6 系統(tǒng)實(shí)物圖Fig.6 Physical system diagram

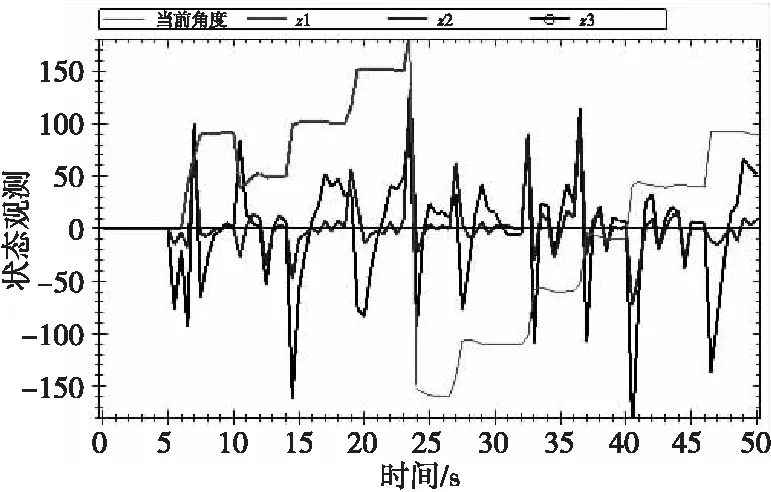
圖7 狀態(tài)曲線圖Fig.7 State curve

圖8 系統(tǒng)響應(yīng)曲線圖Fig.8 System response curve

4 結(jié)論

本文提出了基于模型補(bǔ)償自抗擾的彈體滾轉(zhuǎn)角控制策略。該控制策略通過(guò)建立彈體滾轉(zhuǎn)角控制系統(tǒng)的數(shù)學(xué)模型，建立了以反作用飛輪角加速度為控制量輸入，彈體滾轉(zhuǎn)角為輸出的系統(tǒng)擴(kuò)張狀態(tài)空間模型，進(jìn)而建立了擴(kuò)張狀態(tài)觀測(cè)器，并將觀測(cè)器的觀測(cè)值又作為已知模型信息，在控制器中對(duì)觀測(cè)的干擾進(jìn)行補(bǔ)償。通過(guò)對(duì)收斂性與跟蹤誤差進(jìn)行分析，證明了所設(shè)計(jì)的模型補(bǔ)償自抗擾控制具有很好的收斂性與跟蹤性能，能夠?qū)崿F(xiàn)對(duì)系統(tǒng)狀態(tài)變量和擾動(dòng)的無(wú)差估計(jì)。仿真實(shí)驗(yàn)和實(shí)物實(shí)驗(yàn)驗(yàn)證結(jié)果均表明，本控制策略減小了系統(tǒng)調(diào)節(jié)時(shí)間與穩(wěn)態(tài)誤差，大大增強(qiáng)了其抗擾能力與魯棒性，在工程領(lǐng)域具有較高應(yīng)用價(jià)值。