例談三角形中最值問題的解題策略

江蘇省金湖中學 (211600) 張太清

解三角形的題目是高考中的熱點之一，也是考查解決問題能力的一個著力點，而其中求三角形中的最值問題比較突出，與其它知識點聯合出題是其主要特點．對于如何求最值，常見的方法是運用基本不等式，也可以利用二次函數和三角函數的有界性解決，本文通過舉例分析來探討幾個典型問題的解題策略，務求為讀者帶來點滴幫助．

一、探求角的最值

一般都是對題設條件進行邊角轉換，變形化簡，最后成為一個關于某一個角的三角函數值的范圍，然后根據三角形中角的范圍確定最值．

例1 在△ABC中，角A，B，C所對的邊分別為a，b，c，且a，b，c成等差數列，求角B的最大值．

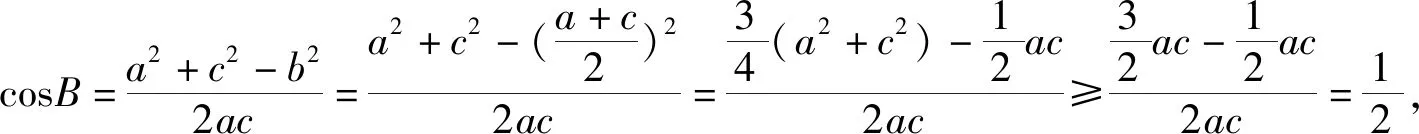
評注：題設中給出的關于三角形邊的條件比較多，運用余弦定理解題是首選，注意此時選定的角要有針對性，大多是解決問題的對象，也可以是受條件的引導．

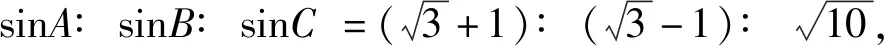
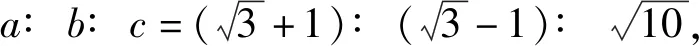
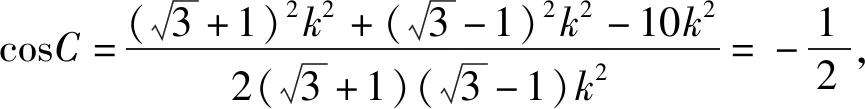
評注：首先通過用正弦定理實現了邊和角之間轉換，然后就是判斷出最大角，而對于用比例系數表示出三角形的三邊也是重要舉措，必須考慮到如何消去參數的后續問題．

二、探求邊的最值

此類問題是體現解三角形中邊角轉換典型的形式，在轉化為邊的問題時，多采用基本不等式解決，如果轉化為三角函數，就用三角函數值的有界性求解．

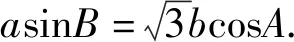
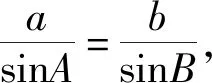
評注：在已知一條邊長后，再求三角形的周長，只需整體解決另外兩邊的和就行了，這點思考很重要，而用余弦定理是容易達到目的的．

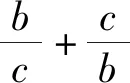
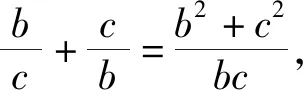
評注：本題解決的關鍵是“BC邊上的高AD=BC”的利用，根據兩個不同的面積公式將邊與角拉上了關系，使抽象的長度比轉化為三角函數的最值問題，揭示了問題的真面目．

三、求三角形面積的最值

三角形的面積公式比較多，選用誰必須目標明確，其標準就是能否運用現有的條件達到解題目的，解題中還需注意公式的整體使用的技巧．

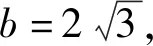
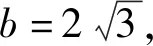
評注：本題中在解決面積的最大值問題時運用了基本不等式，這也是正弦定理和余弦定理的常見的應用之一，抓住條件、瞄準目標、整體變形是有效的解題方法．

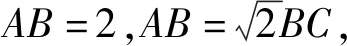
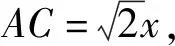
評注：在解題中利用了“三角形中任何兩邊之和大于第三邊”這一知識點確定出邊長的范圍，是解決最值問題的不可缺少的部分．

四、有關三角函數式的最值

解決此類問題中的一個關鍵步驟就是運用已知條件對函數式進行化簡，這其中的正、余弦定理的運用，三角形內角和定理運用都起到重要作用．

例7 已知A，B，C為△ABC的三個內角，若cosA>0，且cos2A-3sinA+1=0，求sin(C-A)+

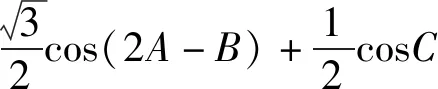
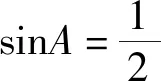
評注：通過運用三角變換把已知條件中的等式化簡求解，得到了其中的一個角，這樣為消元將結論式轉化為關于一個角三角函數提供了有力支撐．還需注意三角形內角和定理的及時運用．

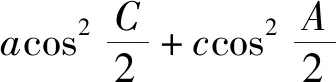
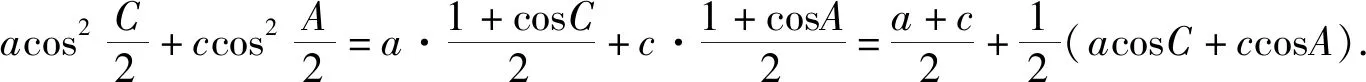
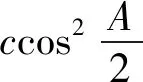
評注：首先運用余弦定理將角的函數式轉化為邊的關系是解題的重要舉措，在解決最值問題時及時運用基本不等式也是解題的精彩之處．

前面我們講解了解三角形中的四類常見的最值問題，當然還有其他情況，限于篇幅只能如此了，此類題目比較綜合，有一定的難度，但只要我們老師能點其精、涉之廣，在教會方法上下工夫，這些問題就能順利解決．