基于MATLAB的六足機(jī)器人運(yùn)動(dòng)學(xué)分析仿真

劉園園

（長(zhǎng)安大學(xué)工程機(jī)械學(xué)院，陜西 西安 710064）

0 前言

隨著科技的發(fā)展，機(jī)器人已逐漸成為學(xué)者研究的熱點(diǎn)，而六足機(jī)器人作為典型的并聯(lián)結(jié)構(gòu)機(jī)器人，運(yùn)動(dòng)方式多變，適合復(fù)雜的地面環(huán)境，以其優(yōu)越的越障能力在諸多機(jī)器人中脫穎而出，已成為近年來的研究熱點(diǎn)。本文對(duì)六足機(jī)器人的運(yùn)動(dòng)學(xué)進(jìn)行了研究計(jì)算，并在Simulink中進(jìn)行了仿真分析[1]。

1 正運(yùn)動(dòng)學(xué)求解

文獻(xiàn)[2]詳細(xì)介紹了旋量理論，本文通過旋量理論搭建如圖1所示的單腿模型，并作為初始位置，其關(guān)節(jié)軸線上點(diǎn)rn（n=1，2，3）坐標(biāo)相對(duì)于基坐標(biāo)系位置關(guān)系如圖1所示，其中L1=45mm，L2=75mm，L3=135mm。

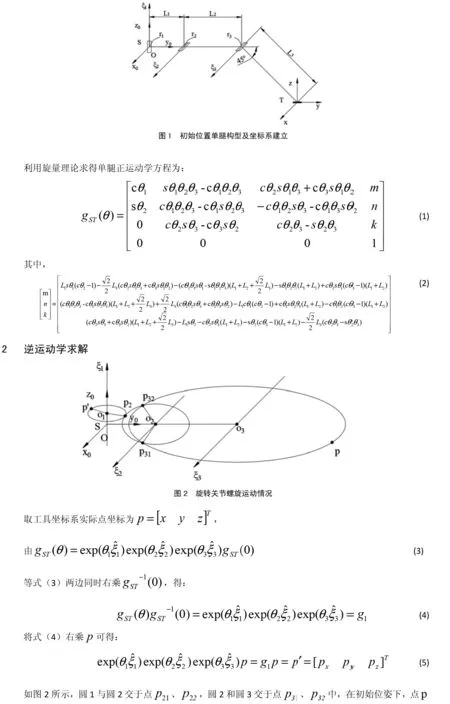
圖1 初始位置單腿構(gòu)型及坐標(biāo)系建立

利用旋量理論求得單腿正運(yùn)動(dòng)學(xué)方程為：

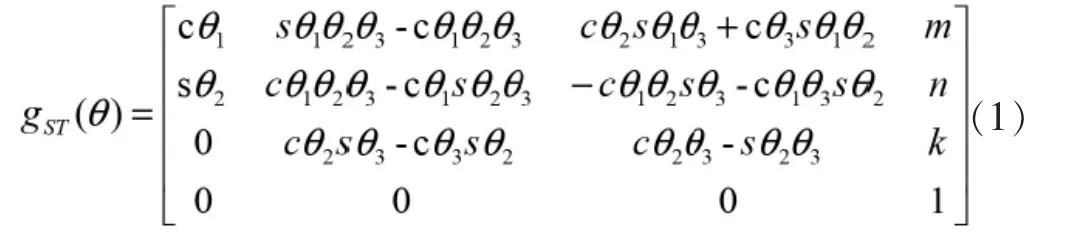
其中，

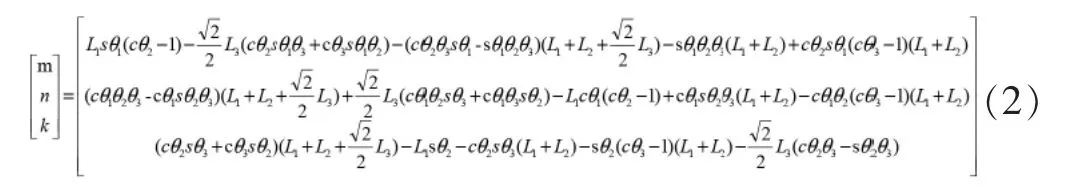
2 逆運(yùn)動(dòng)學(xué)求解

圖2 旋轉(zhuǎn)關(guān)節(jié)螺旋運(yùn)動(dòng)情況

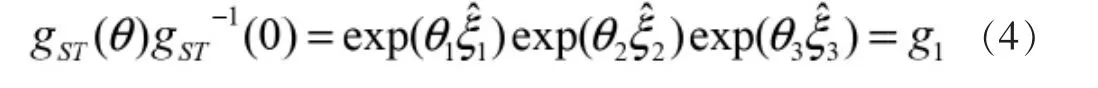
將式（4）右乘可得：

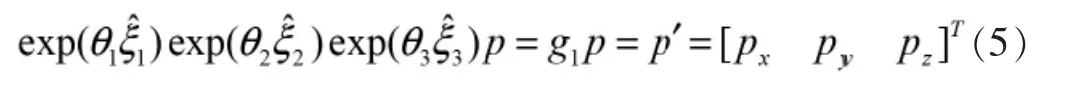
如圖2所示，圓1與圓2交于點(diǎn)p21、p22，圓2和圓3交于點(diǎn)p31、p32中，在初始位姿下，點(diǎn)p通過軸線ζ3旋轉(zhuǎn)θ3到點(diǎn)p3，之后通過軸線ζ2旋轉(zhuǎn)θ2到達(dá)點(diǎn)p2，最后通過軸線ζ1旋轉(zhuǎn)θ1到點(diǎn)p'。因此，需要計(jì)算出各個(gè)交點(diǎn)坐標(biāo)，由圖2可知：

其中：y2、p2x和p3x是未知參數(shù)，y3=L1+L2，y2=L1根據(jù)幾何關(guān)系可建立方程：

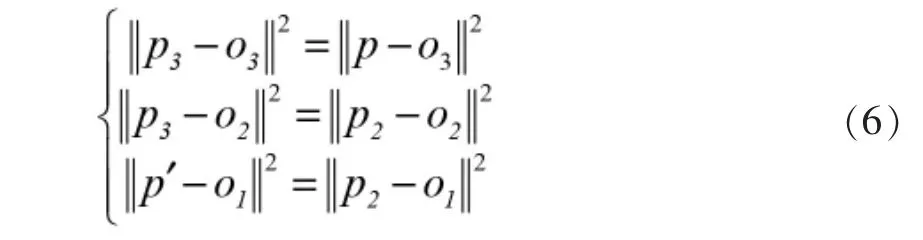
至此，交點(diǎn)p2、p3已經(jīng)求出，所以3個(gè)旋轉(zhuǎn)關(guān)節(jié)螺旋運(yùn)動(dòng)可表示為：

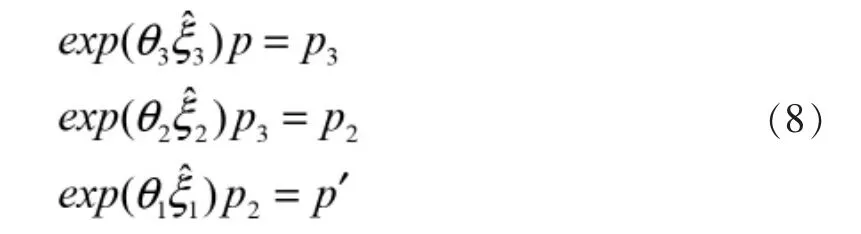
分別利用Paden-Kahan子問題1可求得前3個(gè)關(guān)節(jié)角度為：

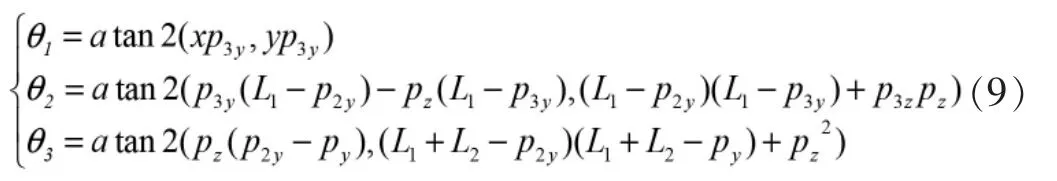
3 基于MATLAB/Simulink的運(yùn)動(dòng)學(xué)仿真

如圖3所示，將CATIA搭建的六足機(jī)器人三維模型導(dǎo)入到Simulink中，然后根據(jù)運(yùn)動(dòng)學(xué)分析結(jié)果計(jì)算出六足機(jī)器人的運(yùn)動(dòng)空間，并進(jìn)行步態(tài)規(guī)劃獲得步態(tài)信號(hào)，并將其添加至仿真中，最后在仿真環(huán)境中添加地面信息，其最終的Simulink仿真圖如圖4所示，由最終的動(dòng)態(tài)仿真結(jié)果觀察可得六足機(jī)器人可以在平坦地面正常運(yùn)動(dòng)行走，驗(yàn)證了運(yùn)動(dòng)分析的正確性。

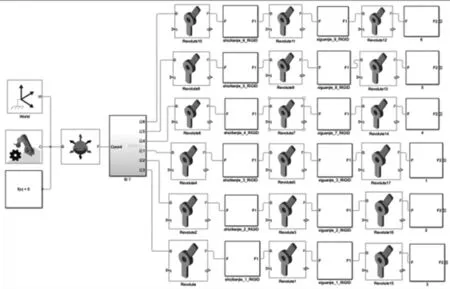
圖3 六足機(jī)器人本體Simulink仿真圖

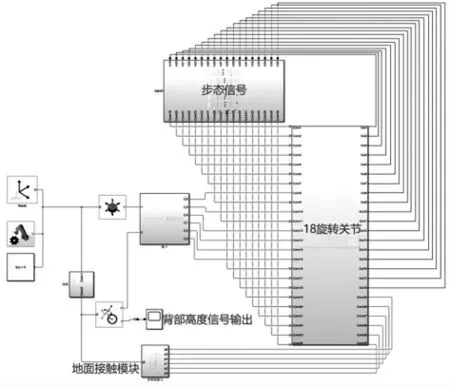
圖4 最終仿真環(huán)境搭建

4 結(jié)論

本文依據(jù)旋量理論對(duì)六足機(jī)器人進(jìn)行運(yùn)動(dòng)學(xué)分析，搭建正逆運(yùn)動(dòng)學(xué)模型，并于MATLAB/Simulink仿真環(huán)境中驗(yàn)證了運(yùn)動(dòng)分析的正確性，為后續(xù)六足機(jī)器人運(yùn)動(dòng)平穩(wěn)性的研究奠定了良好的基礎(chǔ)[3-4]。