燃氣發動機廢氣再循環隨機調節控制器設計
楊君,王明杰,李延驍
1.山東交通學院 汽車工程學院,山東 濟南 250357; 2.山東交通學院 機動車檢測實驗中心,山東 濟南 250100
0 引言
本文中建立燃氣發動機缸內廢氣總質量的離散動態模型,設計基于離散動態模型的隨機調節器,可調節缸內廢氣總質量到其設定值的鄰域內,并通過仿真計算隨機調節器在3種工況下的調節效果。
1 隨機調節器設計
設計燃氣發動機缸內廢氣總質量的隨機調節器,定義缸內廢氣總質量與缸內吸入空氣質量、噴入缸內燃氣質量之和的比值
(1)
式中:k為循環數,mr(k-1)為第k-1循環排氣沖程完畢時缸內殘余的廢氣質量,me(k-1)為第k-1循環再循環廢氣質量,man(k)為第k循環缸內吸入空氣質量,λd為理想空燃比,man(k)/λd為第k循環噴入缸內燃氣質量。
參照文獻[7],定義排氣沖程完畢時缸內殘余的廢氣質量與進氣沖程完畢時缸內混合氣質量的比值
(2)
由(1)和(2)可得:
(3)
令第k循環缸內廢氣總質量為mEGR(k),即
(4)
將式(4)代入(3)可得:
整整三個月,阿東沒有出門,他在家里讀書。老巴很高興,他喜歡兒子這樣。就算沒有賺錢,但讀書畢竟是正經事。而且,心里有大志向的人,才會這樣去讀書。
(5)
式(5)即為缸內廢氣總質量的離散動態模型。由文獻[8]可知,可將r2(k)建模為有限狀態齊次馬爾科夫鏈,其一步預測模型為

定義:考慮離散跳變系統
z(k+1)=Λ(r(k))z(k),
(6)
式中:z(k)為系統狀態,Λ(r(k))為系統矩陣,r(k)為有限狀態齊次馬爾科夫鏈。若對于任意的初始條件(z(0),r(0)),存在一個有限界Ω(z(0),r(0))>0,使得
式中E為期望算子。則稱系統(6)是隨機穩定的。
引理:對于系統(6),若對于給定的正定對稱矩陣Φ(ri)>0,i=1,…,N,存在正定矩陣γ(ri)>0,i=1,…,N,使得
式中pij為r(k)的一步轉移概率,則系統(6)是隨機穩定的。
定理:對于缸內廢氣總質量的離散動態模型(6),設計再循環廢氣質量
(7)
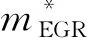
證明:選取李雅普諾夫函數為
(8)
其中c(si)>0為設計參數。對(8)取差分,可得
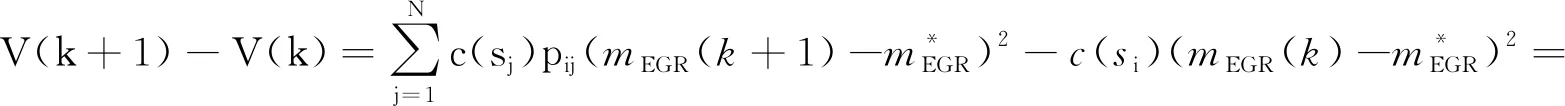
(9)
將(7)代入(9)可得
因此,由引理可知,由(6)和(7)組成的閉環系統是隨機穩定的。
2 數值仿真驗證
對設計隨機調節器(7)的數值仿真驗證。基于缸內廢氣總質量的離散動態模型(5)和文獻[11-14]中的均值模型,搭建了如下具有EGR系統的燃氣發動機數值仿真模型:
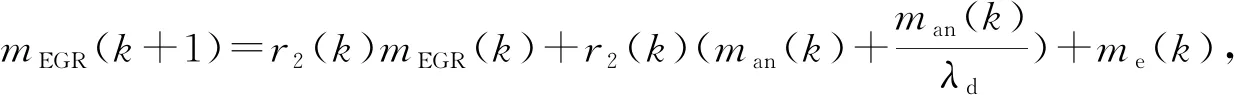
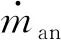
式中:s為函數ψ(s)的自變量,k為比熱比。數值仿真結構如圖1所示。
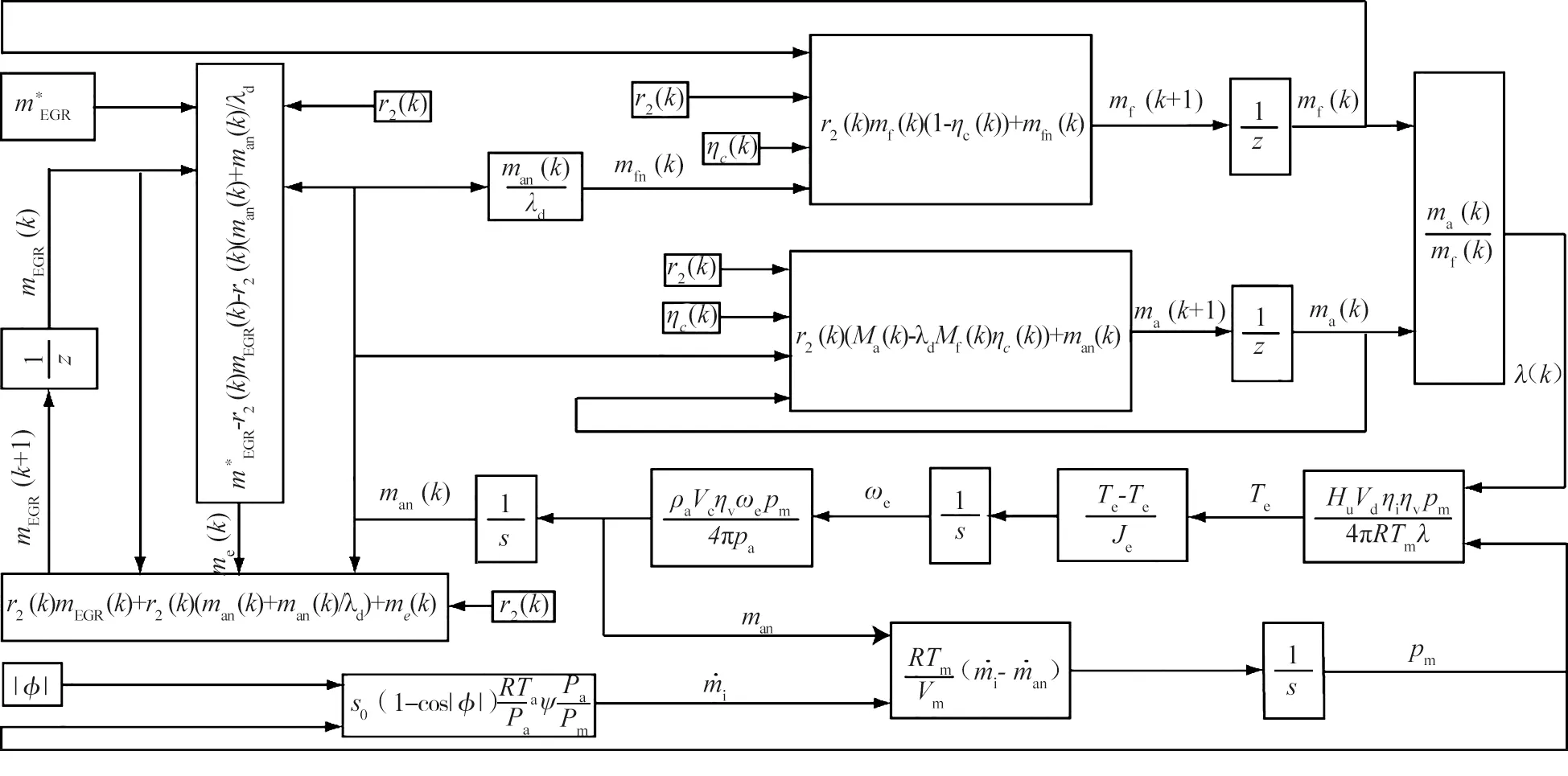
圖1 數值仿真結構圖
數值仿真在3種工況下運行,3種工況的具體參數如表1所示,3種工況下的缸內廢氣總質量和再循環廢氣質量如圖2~7所示。

表1 數值仿真工況
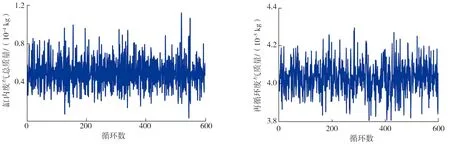
圖2 C1工況下缸內廢氣總質量 圖3 C1工況下再循環廢氣質量
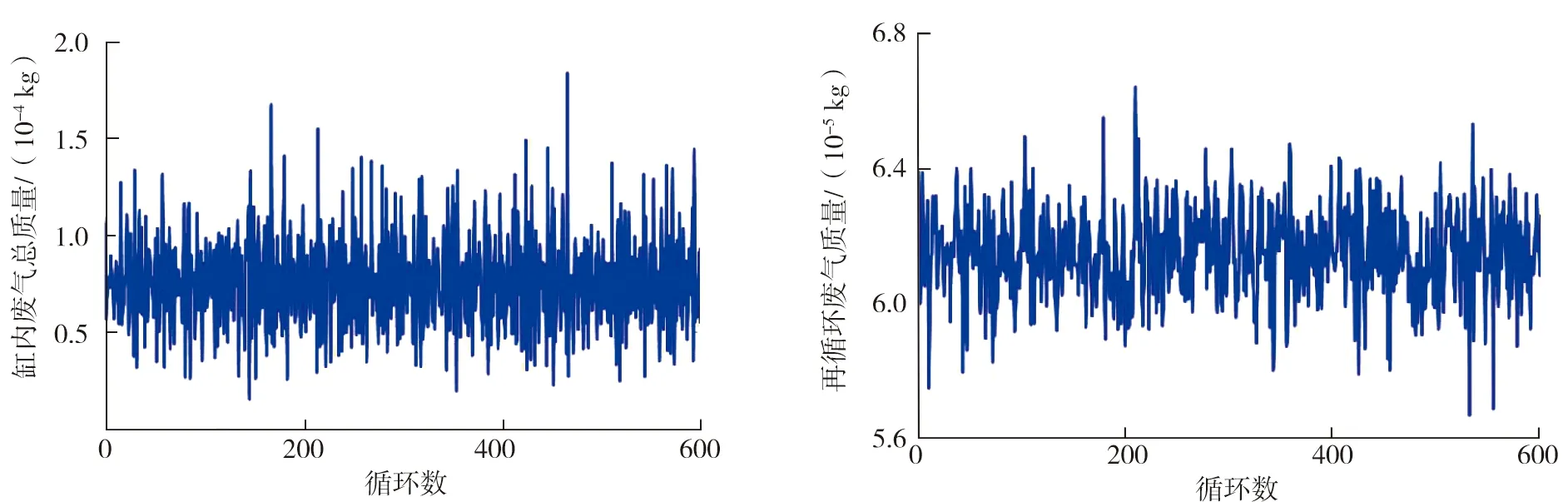
圖4 C2工況下缸內廢氣總質量 圖5 C2工況下再循環廢氣質量
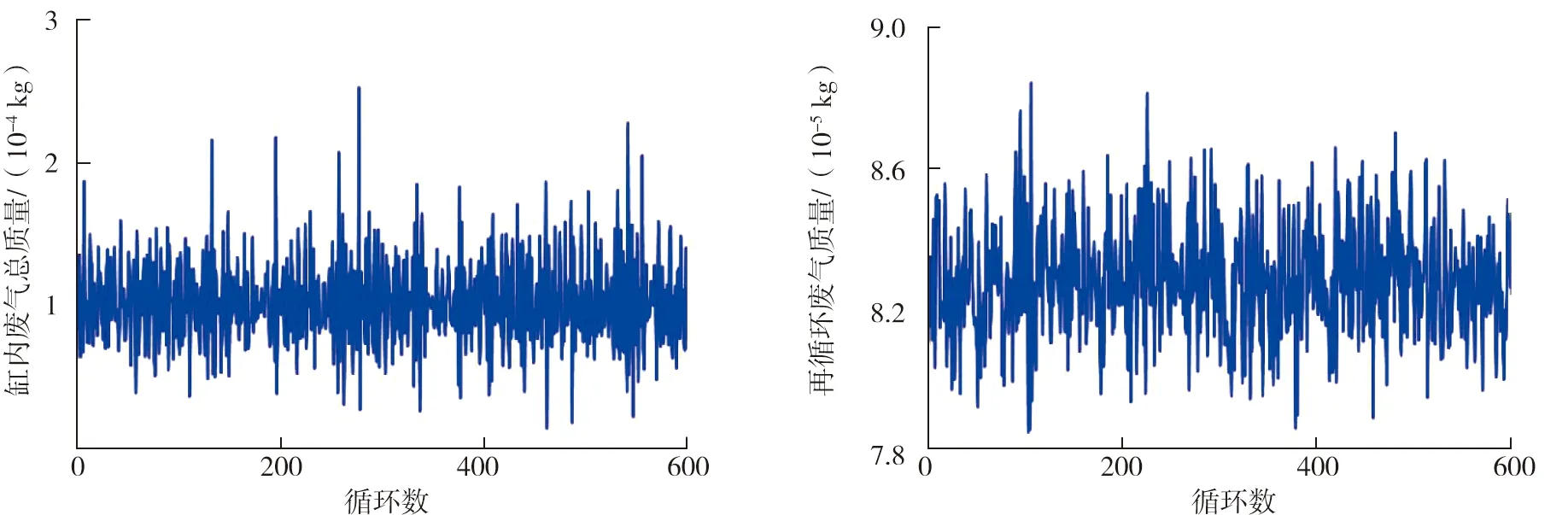
圖6 C3工況下缸內廢氣總質量 圖7 C3工況下再循環廢氣質量
由圖2~7可知,所設計的隨機調節器(7)在C1、C2、C3三種工況下均能將缸內廢氣總質量調節到其設定值的鄰域內,且再循環廢氣質量有界。
3 結論
1)建立了缸內廢氣總質量的離散動態模型。
2)基于建立的離散動態模型,設計了缸內廢氣總質量的隨機調節器。
3)通過數值仿真驗證了所設計隨機調節器的有效性,即在3種工況下均能將缸內廢氣總質量調節到其設定值的鄰域內。

