基于質量源法的全墊升氣墊船興波模擬研究

陳熙， 朱仁傳， 顧孟瀟， 高嵩

(1.上海交通大學 海洋工程國家重點實驗室，上海 200240；2 上海船舶及海洋工程設計研究院，上海 200011)

氣墊船是以靜態空氣壓力支撐的一類高性能船[1]，其中依靠全部靜態空氣壓力支撐且速度較高的類型為全墊升式氣墊船ACV。該類型氣墊船在航行中的阻力絕大部分來自于興波阻力，探究氣墊面興波的實質及與一般排水型船舶的異同，厘清其與航速、主尺度、氣墊壓力、噴氣流量等參數之間的關系，建立求解興波阻力的方法，對于氣墊船快速性優化、及后續圍裙動力學和氣墊空氣動力學[2]的研究具有重要意義。

研究氣墊船興波問題的方法主要有3大類：模型試驗、理論方法及數值方法[3]。Newman等[4]提出了氣墊做勻速直線運動的興波阻力計算方法，將氣墊簡化為一個作用在水面上的壓力面，面上壓力分布均勻，并給出了相應工況下的興波阻力系數圖譜，后續學者研究多基于此來參照。Barratt[5]針對氣墊底部不同壓力分布時的情況，提出了淺水中的興波阻力計算方法，結果表明興波阻力的峰值隨著流域的加深而提前發生，但是因其假設興起的波浪是微幅波，其結果均較大于試驗結果。Newman等[4]提供的圖譜在中高速時與試驗結果吻合良好，然而針對低速情況下的圖譜結果出現了稠密的峰谷波動，與試驗不符。Doctors[6]針對該問題提出了新的氣墊底部壓力分布方式，其假定底部為雙曲正切分布，而非之前給定的均布壓力，計算表明在阻力峰出現之前沒有出現稠密的峰谷波動，彌補了Newman圖譜的不足。同時，Doctors采用該方法研究了氣墊船在淺水中直航的阻力性能，結果表明淺水會使興波阻力增大。Lazauskas[7]采用線性理論方法預報了氣墊船非勻速航行時的阻力性能。Mileewski[8]運用流體仿真軟件計算分析了氣墊船航行時船身四周的興波波形。Nikseresht等[9]模擬了全墊升式氣墊船氣室內部氣墊的空氣流動，指出氣墊的壓力分布、航速等因素極大的影響了其興波阻力與興波波形。Bhushan[10]等運用線性理論和非線性理論2種方法對深淺水下不同壓力面形狀的氣墊興波阻力進行了計算分析，結果表明非線性理論更有利于計算淺水中的阻力性能。Kevin等[11]對線性方法和有限體積法這2種方法進行了對比，指出2種方法對計算較高速段的興波阻力的準確性很高，而因低速時非線性影響的增強，線性方法不再穩定。劉寧[12]對全墊升式氣墊船在波浪上航行的運動響應進行了研究，考慮若干非線性因素的影響，分析了圍裙觸水的影響。

前人的研究多是給定氣墊面壓力分布模擬興波情況，而不同航速下適宜的壓力分布情況較難把握，且實際情況中氣墊船無法直接控制底部壓力，而是通過控制風機流量來調整船體。本文介紹了求解全墊升式氣墊船興波阻力的基本假設及簡化方法，建立了氣室模型，并引入質量源模擬風機供氣，運用STAR-CCM+商用軟件，對興波阻力進行了計算，并與多個文獻計算結果進行對比，驗證了該方法的有效性。此外，采用該方法研究了淺水中氣墊船的興波阻力變化情況。

1 氣墊船興波模型及數值計算

氣墊興波數值模擬在一個三維數值水池中進行的，在出口處和遠離船體的邊界處設有人工阻尼消波區。以兩相流假定為基礎，自由面沒有擾動時，其上部為空氣，下部為水。

為模擬全墊升式氣墊船在正常航行中的興波情況，將其放置在一個以兩相流假定為基礎的三維數值水池中進行。采用固定在船上并隨船以定常速度航行的參考坐標系來模擬計算興波情況。因全墊升氣墊船是一個多自由度非線性復雜系統，其中耦合了氣墊、圍裙、水面等多方面的影響，本文僅對興波情況進行模擬，作如下簡化假定：

1)氣墊船高速航行中，其水動阻力主要由氣墊下表面與圍裙觸水的興波阻力及圍裙濕表面的摩擦阻力3部分構成，本文假設船體正常航行，圍裙不觸水，即水動阻力只有氣墊的興波阻力。同時將圍裙視作剛性，簡化氣墊船上層建筑及船體結構。

2)所研究的工況為氣墊船穩定航行，不考慮船體姿態變化，且氣墊底部壓力分布達到穩態，在氣室風機口加入質量源來模擬供氣，從而達到墊升船體、作用水面的效果。

3)因上述假定，氣墊船穩定航行，船體與水沒有接觸，不存在水動摩擦阻力，因此不考慮粘性，視為理想流體，Bhushan等[9]的研究也表明在研究氣墊船純興波問題時，不考慮粘性的結果與RANS方法差異相當小。

1.1 控制方程

本計算模型中的流場是三維不可壓縮理想流體，流場應滿足連續性方程和歐拉方程：

(1)

(2)

采用流體體積函數(volume of fluid，VOF)法追蹤自由面。控制體內水的體積占控制體總體積之比定義為水的體積分數α，空氣的體積分數即為(1-α)。該模型假定水和空氣共享速度和壓力場，可將其看作一種等效流體，故只要處理和單相流相同形式的質量、動量守恒方程，該等效流體的密度為：

ρ=αρw+(1-α)ρa

(3)

式中下標w、a分別指代水和空氣。體積分數滿足連續性方程：

(4)

方程(1)、(2)、(4)組成了氣墊興波模擬數值水池的控制方程。該方程組與一般的N-S方程相比，忽略了粘性項的影響，同時引入了附加質量源項q。

1.2 質量源模擬風機系統

全墊升氣墊船正常航行過程中，墊升風機向船體氣道供氣，氣體經過圍裙進入氣室，形成氣墊將船體全部托離水面，因墊升后船體距離水面有一段距離，氣體會通過囊指下側縫隙溢出，因此供氣需持續穩定。圖1為氣墊船橫剖面的示意圖。

如前述假設2，為模擬出氣墊施加于水面的效果，簡化氣墊船結構，僅對氣室區域進行建模，如圖所示為氣室橫剖面圖。采用三維質量源方法[13]模擬風機不斷給氣室供氣。

圖2 簡化氣室橫剖面Fig.2 Cross section diagram of simplified chamber

式(1)、(2)中引入的質量源項q表達式為：

(5)

式中：Ωs為質量源區域，即圖中虛線框住的部分；Δz為質量源區域的厚度；vair為模擬風機吹氣口的空氣速度；q的單位為s-1。通過在該區域添加與空氣進氣速度有關的質量源項，產生供氣效果。

在本文的驗證工作中，前人研究的前提多是給定壓力分布情況，因此需要確定質量源項q的大小與氣墊底部壓長比的關系。

Bhushan等[14]給出了由伯努利方程得到的流量公式：

(6)

式中：pc為氣墊面上實際壓強減去標準大氣壓的壓強由氣墊壓長比可得氣墊相對壓強；Q為模擬風機的出口流量，m3/s；Cd為泄漏系數，Faltine建議取為0.6～1.0；Ai為簡化氣室的四周邊界最低點與水面的間隙形成的總面積；ρair為空氣密度。質量源項可通過式q=Q/VΩ求出，其中VΩ為質量源區域的體積。

1.3 興波阻力系數計算方法

全墊升氣墊船在正常航行中，船體并不與水面接觸，難以采用排水型船體的表面壓力積分法求得阻力。本文將簡化氣室和氣墊視為一個整體，通過壓力施加到水面，對氣室正下方與氣墊直接接觸水面的形狀及壓力進行處理，求得內水面所受力，由牛頓第三定律即可得氣墊船受到的興波阻力。

取氣室正下方的水面上一矩形微元面，其長為dL，寬為dB，如圖3所示。

該微元面與水平面夾角為αw，取直角坐標系ξOη,其原點置于前端點O，Oξ軸沿航行方向向后為正，Oη軸垂直于Oξ軸，向下為正。因壓力作用與作用面垂直，則微元面上的壓力為：

Fη=pc(x,y)dBdL

(7)

該力沿船舶方向航行的分力為：

(8)

式中：dξw為微元面的波高；dx為微元面水平面投影的x方向距離。整個氣室正下方水面上沿航行方向受到的總分力Rx可積分得到：

(9)

水面受到的力為氣墊施加于其上的力，由牛頓第三定律，氣室航行時的興波阻力Rw為Rx的反作用力為：

(10)

具體求解采用將積分式離散求和的方法，表達式為：

(11)

在得到興波阻力后，可根據紐曼-波爾的氣墊船興波阻力系數計算出興波阻力系數：

(12)

2 氣墊船的興波波形及阻力計算驗證

影響氣墊船阻力最主要的參數為壓長比，其決定興波阻力特別是越峰阻力的大小。許多學者在研究氣墊船興波問題時，多是指定氣墊底面的壓力分布，針對不同平面形狀的氣墊展開了廣泛研究，其中較為廣泛對照的是紐曼-波爾圖譜，該圖譜給出了指定壓長比的氣墊面在不同傅汝德數下的興波阻力曲線。本文取一種壓長比的氣墊船模型在靜水中航行的興波情況進行研究，以驗證該方法的有效性。

2.1 計算域及邊界條件

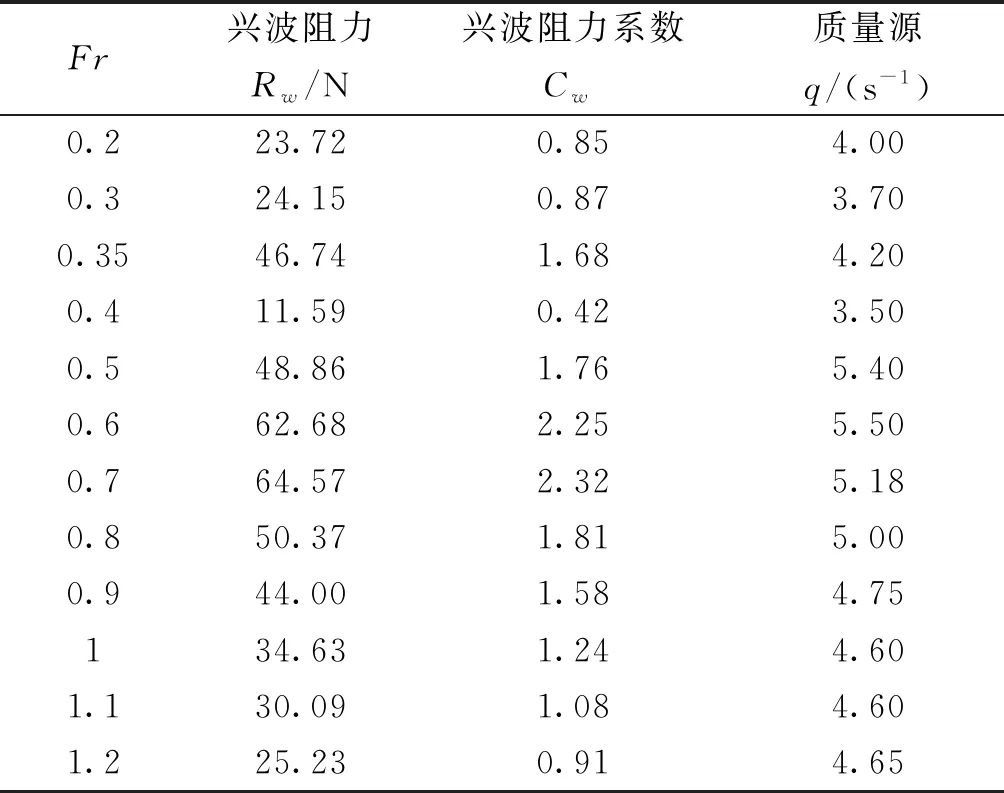
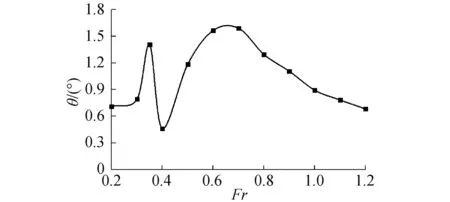
選取氣墊船氣室模型長LC=3 m，寬BC=2 m，氣墊壓長比PC=0.012 7ρgLC，如圖4(a)，并置于圖4(b)所示的數值水池中。計算域原點位于氣墊體的垂直中心線和靜水面的交點處，x軸指向航行方向，沿船舶航行方向為正，y軸指向船寬方向，以船舶右舷為正，z軸向上為正。計算域范圍為：-7LC

圖4 氣室及計算域區域Fig.4 Air chamber and calculation domain

以船舶航行方向視角來定義計算域邊界條件，前邊界面及上下面設定為速度入口，左右面設定為對稱邊界，后邊界面為壓力出口，氣室四壁及頂面為壁面。同時在左右面及后邊界面設阻尼消波區，設定阻尼波長度大致為定常興波波長的2倍，以消除波反射影響結果。

計算網格的劃分如圖5所示，為在保證計算精度的同時提高計算效率，加密部分網格。在凱爾文波系范圍內進行網格加密，精準捕捉波形，防止數值耗散，自由面垂向方向要保證足夠網格，氣室內部特別是質量源區域網格要加密，提高氣體流場信息的準確度。

圖5 計算域網格劃分Fig.5 Grid division of calculation domain

2.2 興波阻力系數計算與對比

對氣墊模型進行了12個傅汝德數下的靜水航行興波模擬計算，在確定質量源q大小時，先根據式(6)估算出大致范圍，因氣室與水面之間圍合區域的面積隨著自由面形狀不同而異，在計算每種傅汝德數的情況時，需微調q的值，使氣墊底面平均壓強大致滿足壓長比的要求。

表1給出了不同傅汝德數下氣墊船靜水航行中的興波阻力及其系數，以及模擬所采用的質量源項的大小。將興波阻力系數隨傅汝德數變化的數據繪制成圖6。

表1 氣墊船興波阻力及其系數計算結果

圖6 氣墊船興波阻力系數隨傅汝德數變化的曲線圖Fig.6 Curve of wave making resistance coefficient of ACV changing with Froude number

由圖6可知，曲線有2個較為明顯的阻力峰，第1個阻力峰發生在Fr為0.35時，第2個阻力峰發生在Fr為0.6附近時。氣墊船底部與水面接觸部分的壓力減去大氣壓力，僅為大氣壓力的2%～6%，壓力沖量相比一般排水型船舶產生的沖量很小。此外，隨著航速提高，水面受到的壓力也不會劇增，因而興波阻力不會隨之大量增加，反而可能會減弱，這是全墊升氣墊船具有高速性能的原因之一。

圖6中給出了其他學者在相同工況下的模擬結果。本文的結果與Bhushan[7]的CFD方法較為吻合；與Everst等[15]的試驗結果相比，曲線變化趨勢尤其是2個阻力峰發生的傅汝德數基本一致。總體來看，本文計算氣墊船興波阻力的方法具有一定有效性和可靠性。

2.3 興波波形分析

圖7給出了5個不同傅汝德數時氣墊船靜水航行時的自由表面興波波形。可以看出，低速時，凱爾文波系中的橫波較為明顯，隨航速的增加，橫波不再明顯，凱爾文角逐漸減小，氣墊壓力中心逐漸后移。

圖7 氣墊船自由面興波Fig.7 Waveform inducing by ACV

圖8給出了4種工況下計算域中縱剖面上的自由面升高圖。圖中的橫坐標x/LC為縱向長度和氣墊船長的比值，0為氣墊船縱向中點的位置。結合圖8，在航速較低(Fr=0.3)時，在氣墊船區域有2個較為明顯的波谷，隨著航速增大，氣墊區域第1個波谷的位置不斷后移，當Fr為0.7時已處于船體后部。圖中也可看出氣墊深度隨航速的變化，在Fr為0.7附近時有極大值，當傅汝德數偏離0.7時，氣墊深度有減小的趨勢。

圖8 氣墊各航速下中縱剖面自由面升高曲線Fig.8 Free-form surface elevation curve of mid-longitudinal section at each speed of air cushion

進一步分析波形，計算出各個航速下氣墊正下方興波水表面的平均縱傾角θw，如圖9所示。

圖9 氣墊下方水表面平均縱傾角隨航速的變化曲線Fig.9 Curve of average pitch angle of water surface under air cushion with speed

對比興波阻力系數變化圖(圖6)和平均縱傾角變化圖(圖9)可見，兩者變化趨勢十分相似，平均縱傾角在Fr=0.35及Fr=0.6附近各有1個峰值。

因此，在氣墊船底部壓力一定的情況下，興波阻力的主要影響因素之一是氣墊下方水表面的平均縱傾角。氣墊壓力的強度與航速關系不密切，航速更多地影響底部波形分布，因此在后續對氣墊船阻力性能研究中應著重關注設計航速下的氣墊底部波形分布。

3 淺水中的氣墊船興波阻力變化

氣墊船因具有兩棲性能，對淺水中氣墊船的阻力特性進行研究具有研究意義。前文針對深水情況的氣墊船興波情況進行了計算研究，驗證了該方法的有效性與可靠性，可運用該方法對淺水中氣墊船的興波阻力變化情況進行研究。

針對近似無限水深(d/Lc=4)和極淺水(d/Lc=0.25)2種情況，分別計算了10個傅汝德數下靜水航行的興波阻力系數。氣墊及流域參數如表2所示。

表2 氣墊船及流域參數Table 2 Parameter of ACV and flow field

與第2節中控制底部壓力分布情況不同，本節控制質量源項，即各航速下的進氣流量保持一致，如此設置更接近真實情況，試驗中控制風機流量較控制底部壓力也更為便捷，方便對比結果。模擬得到的結果如圖10所示。

圖10 2種不同水深下的氣墊船興波阻力系數曲線Fig.10 Curve of wave resistance coefficient of ACV under two different water depths

由圖10可知，水域的深淺對興波阻力影響很大，具有較為顯著的淺水效應。淺水(d/L=0.25)與深水(d/L=4.0)下氣墊船均有2個阻力峰，第1個阻力峰的位置兩者基本相同，淺水的第1個阻力峰值較低，而淺水下的第2個阻力峰發生在Fr=0.5附近，深水發生在Fr=0.7左右，淺水的第2個阻力峰值顯著大于深水的值。在越過阻力峰后，淺水下的阻力值較深水下要低。

因此氣墊船的淺水效應大致與常規船型的規律一致，在臨界速度附近阻力會出現極大值，一般為氣墊船興波的第2個阻力峰，在相關設計時需考慮該處影響。

4 結論

1)文中計算了不同航速下給定平均壓力值的氣墊船興波阻力，結果準確給出了氣墊船興波阻力隨速度變化的2個明顯的阻力峰，與相關實驗結果對比吻合良好。

2)運用同一方法對淺水中的氣墊船興波阻力變化情況進行了研究，表明氣墊船同樣有淺水效應，在臨界速度時興波阻力會出現極大值，也是第2個阻力峰出現的位置。

綜上可知，論文提出的質量源方法結合CFD平臺可以模擬移動氣墊引起的水表面變形，方法簡單、計算穩定、高效，能夠獲得準確的興波阻力，較為客觀反映實際氣墊船移動興波特性。