問題導學，讓數學學習走向本質理解

葛敏輝

[摘 要]“小數點搬家”的學習內容主要是探索小數點位置移動引起小數大小變化的規律，緊扣本質提出問題，通過問題導引學習，可以讓學生真正理解規律背后的數學本質。通過問題導學，激活學生已有的知識和經驗，層層深入地引領學生探索規律、深化理解，從而體會到十進位值制的優越性。

[關鍵詞]理解;本質;問題;導學

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）05-0011-04

“小數點搬家”這一課在不同的教材里有不同的要求，有些教材單獨給它安排了1課時，有些教材卻沒有。這一內容到底該不該教？如果教，要教給學生什么？怎樣才能幫助學生理解這個規律背后的數學本質？這值得一線教師深入思考、探索和實踐。

一、學前思考

（一）教之困——可以不教嗎？

北京海淀區中關村第一小學的陳千舉老師通過研究發現，不管有沒有專門學習“小數點搬家”這一內容，學生在解答相關題目時并沒有明顯差異。那么，有的教材為什么要安排這一內容呢？

（二）學之惑——小數點會搬家嗎？

在學習“小數點搬家”的過程中，經常有學生產生疑問：小數點一直在數的整數部分和小數部分的中間，并沒有“搬家”，教材是不是錯了？數學課堂應關注學生的真問題，以問導學，所以本節課就可以這個問題為核心，引領學生深入探究“小數點會搬家嗎？到底是誰在搬家？為什么叫小數點搬家？”這樣，有了真問題的課堂，學習才會真正發生。

（三）學情分析——理解水平如何？

為了了解學生對于“小數點搬家”的理解水平，筆者對四年級130名學生進行問卷調查。

【問題1】觀察0.01、0.10、1.00這組數據，小數的大小發生了什么變化？

[ 特征描述 占比 水平0 錯誤描述 3.1% 水平1 籠統描述“從小到大” 14.6% 水平2 描述“相差關系” 3.8% 水平3 描述“倍比關系” 78.5% ]

通過分析數據發現，在學習“小數點搬家”之前，已經有78.5%的學生能描述數據之間的倍比關系。那么學生是否能解釋這種變化？為此，筆者隨機對40名學生進行了訪談，其中有24名學生可以借助十進制、位值制來解釋這種變化，有3名學生能借助元角分來解釋，二者占全部學生的67.5%。

【問題2】你認為是誰的變化引起小數的大小發生變化？

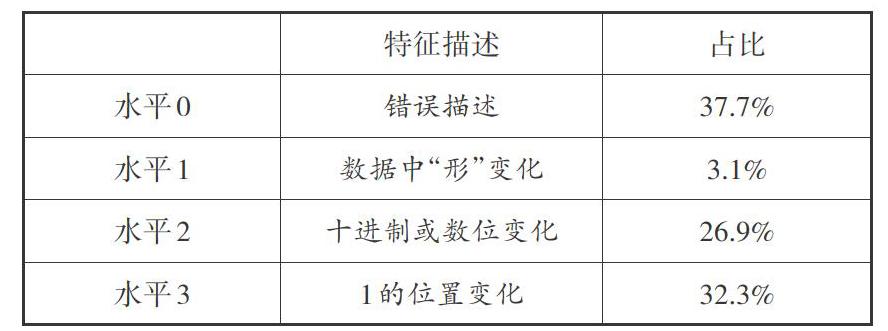
[ 特征描述 占比 水平0 錯誤描述 37.7% 水平1 數據中“形”變化 3.1% 水平2 十進制或數位變化 26.9% 水平3 1的位置變化 32.3% ]

水平1的學生關注的是數據中形的變化，包括0的位置變化、0和1的位置交換以及“小數點的搬家”;水平2的學生能結合十進制、數位等已有知識關注到“十進制或者數字的數位發生變化，引發這組小數大小的變化”;水平3的學生能感受到“因為1所在的數位不同，所以位值不同引發了數據的變化”的本質。

基于以上情況，筆者有了以下的學習活動設計：學生已經可以借助數位順序表、十進制、位值制等知識描述0.01、0.10、1.00的大小變化及關系，且思維已有一定的抽象水平，因此教材中大篇幅地借助元角分以及直觀模型圖來說明大小關系這個環節可以刪去;可以問題引導學生通過遷移、自學、觀察、比較、辨析等深度理解“小數點搬家”的本質，促進學生思維的生長。

二、學習活動

（一）任務驅動，喚醒學習經驗

1.觀察數字1在數位順序表中的位置變化，初步感知數的大小變化

師：大家已經很熟悉數位順序表了。數字1在個位安了一個家，你說這是幾啊？（在數位順序表的個位貼上“數字1”）

生1：1。

師：這個1很調皮，它想“搬家”了，它“搬到”了十位，這時候你會用哪個數來表示呢？

生2：10。

師：為什么要在1后面添1個0？

生3：因為沒有0它就變成了1。

生4：要用0占位。

師：你發現了什么？

生4：數字1“搬家”后，改變了位置，數的大小也變了。

生5：1擴大了10倍，變成了10。

生6：乘10，1×10=10。

師：也就是，“1→10”得到的數是原數的10倍（也就是乘10）。

2.深入體驗，發現數字移動位置的變化規律

師：現在數字1又“搬家”了（數字1移到百位），這時是什么數？

生7：100。

師：你們還發現了什么？

生8：1從十位移到百位，擴大了10倍。

生9：1在不同的數位上就會得到不同的數。

生10：數字“搬家”會引起數的大小發生變化。

師：如果1又“搬家”了，從百位“搬回”到十位，數又發生了什么變化？

生11：從百位到十位，100變成了10，相鄰兩個單位之間的進率是10，所以縮小了十倍。

師：你們說的縮小了十倍，除以10，也就是平均分成10份，取一份，也可以說得到的數是原數的十分之一。假如移到個位呢？

生12：從100到1，得到的數是原數的百分之一。

生13：從10到1，得到的數是原數的十分之一。

師：通過剛才的活動你有什么發現？

生14：數字1從個位移到十位，數擴大10倍;從個位移到百位，數擴大100倍。

生15：增大一位（指移到高位），得到的數是原數的10倍。如果倒退一位（指移到低位），得到的數是原數的十分之一。

生16：數字1往左“搬”一位，就擴大到原來的10倍，往左“搬”兩位，就擴大到原來的100倍。

生17：數字1往左“搬”一位就乘10，往右“搬”一位就除以10。

師：說得真好！為什么變化規律是“移動一位就是10倍”？

生18：因為相鄰兩個計數單位之間的進率是10。

[思考：數位順序表實現了自然數和小數的完美統一，以此為工具，引導學生觀察1在數位順序表整數部分中的位置變化，可以激活學生已有的知識經驗，使學生感悟到“數字搬家”引起數的大小變化的規律和內涵，為學生自主構建規律搭好認知支架。]

（二）自主遷移，構建知識體系

師：是不是只有在整數部分移動位置才有這樣的變化規律？請驗證你的猜想，并在作業紙上寫下來。

生1：小數部分也有這樣的規律。1從十分位移到百分位，也就是0.1到0.01，得到的數是原數的十分之一。

生2：如果反過來，1從千分位移到百分位，也就是從0.001到0.01，得到的數是原數的10倍。從百分位移到十分位，也就是0.01到0.1，得到的數是原數的10倍。（如圖2）

生3：我發現在小數部分和整數部分之間也存在這樣的規律。1從十分位到個位，0.1乘10等于1，1從十分位到十位，0.1乘100等于10。（如圖3）

……

師：能不能對你們發現的規律做個總結？

生4：不管是整數部分還是小數部分，只要數字往高位移動一位，得到的數是原數的10倍，往低位移動一位，得到的數是原數的十分之一。

師：是的，在整個數位順序表上，“數字搬家”1位，都會有10倍的變化規律。為什么有這樣的變化規律？

生5：因為相鄰兩個數位的進率都是10。

[思考：從“數的搬家”入手，通過整數部分的體驗遷移到小數部分，學生自主借助數位順序表，在探究、溝通、聯系的學習中理解“數字搬家”引起數的大小變化規律，充分經歷知識形成和關聯的過程。]

（三）沖突融合，深化規律理解

1.自學反饋，認同課本中關于小數點“搬家”的規律介紹

師：課本是怎么介紹今天學的知識呢？請自學課本第35頁。（學生自學）

生1：一個數的小數點向右移動一位，得到的數是原數的10倍;一個數的小數點向左移動一位，得到的數是原數的十分之一。

師：能不能結合例子說說？

生2：0.01的小數點向右移動一位變成0.1，所以得到的數擴大了10倍;0.1的小數點向左移動一位變成0.01，得到的數是原數的十分之一。

師：這樣的規律在其他小數那里也存在嗎？請舉例驗證。

生3：其他小數也存在這樣的規律。

學生作品（如圖4）：

2. 引發沖突，讓學生深度思辨變化中蘊含的實質

師：我們發現的是“數字搬家”有數的大小變化規律，可是課本上介紹的是“小數點搬家”有數的大小變化規律，到底是誰在“搬家”？

生4：我覺得是“小數點搬家”。

生5：我覺得是“數字搬家”。

師：你同意誰的意見？請說出理由。

生6：我同意“小數點搬家”。比如說8.88乘10等于88.8，小數點前面原來有一個8，擴大10倍后小數點前面有兩個8，“小數點搬家”了。

生7：我同意“數字搬家”。因為小數點是隔開整數部分和小數部分的，不會“搬家”。

師：誰聽懂了生6的意思？

生8：小數點一直在整數部分和小數部分的中間，怎么會“搬家”？

生9：我也認為小數點是不會“搬家”的，在數位順序表上就看得很清楚（上臺演示），它一直是整數部分和小數部分的分界。

師：生6，你覺得呢？

生6：表面上看是“小數點搬家”，其實是“數字搬家”。

師：為什么你改變了想法？

生6：因為小數點在數位順序表中的位置是固定的，其他數字的位置都是可以移動的。

3.思辨交流，體會數學人為規定的合理性

師：是啊，表面上看是“小數點搬家”，但是實際上小數點是不會“搬家”的，其實是數字在“搬家”。那么明明是“數字搬家”，為什么教材卻說是“小數點搬家”？

生6：“小數點搬家”可能更加方便一點。

師：怎么能讓大家看出“小數點搬家”的方便？

生7：0.057×10=0.57，如果說“數字搬家”，5往高位移一位，從百分位移到十分位，7也往高位移一位，從千分位移到百分位。這樣很麻煩！如果用“小數點搬家”，只要說“小數點往右移動了一位”就好了。

師：你們有什么感覺？

生8：這樣的話既可以讓語言變得簡潔，也能說出想表達的意思。

生9：一個數如果數字很多，說“數字搬家”會很浪費時間，說“小數點搬家”就很方便。

師：是啊，確實是“數字搬家”，但是用“小數點搬家”來表達會顯得更方便，因此人們就把這個規律叫“小數點搬家”。

4.練習（略）

[思考：你有什么收獲？你有什么疑問？為什么明明是“數字搬家”，教材卻說“小數點搬家”？三個問題的遞進，讓學生經歷了“平衡—失衡—新的平衡”，第一問發展學生自學和梳理知識的能力，第二問發展學生自主辨析知識的能力，第三問讓學生感悟數學發展的合理性，學生逐步走近知識本質，走向思維生長。]

三、學后反思

（一）緊扣本質提出問題，讓導學有一個靶向

在思考并教學這一內容的過程中，筆者真切感受到，遠離本質的提問和練習，難以讓學生理解本質、舉一反三。本文中的問題指大問題，大問題是指那些直指本質的、涵蓋教學重難點的、具有高水平的、以探究為主的問題。“到底是誰在搬家？”顯然是一個好問題，以此來引導學生深入開展學習，自然事半功倍。

（二）立足學生分析問題，讓數學有一些溫度

在課堂中不難發現，數學知識與學生理解常常是兩張皮，數學變得生硬而難以理解，學生把主要精力花在模仿和操練上，數學似乎顯得有些冰冷。事實上，學生已經知道了什么？疑惑在哪里？有哪些經驗可以支撐他們思考？回歸學生，暴露他們的困惑，讓他們在需要和思考中找到獲得感。這節課的知識對于學生來說，困惑點在“小數點怎么會搬家？”“明明是數字移動，為什么要說成小數點移動？”。學生在自我需求中分析問題、理解規律，從而體會到十進位值制的優越性。如此的活動充滿思考，如此的數學富有溫度！同時，學生在活動中學會了思考，釋放了潛能，生成了智慧。

（三）自主建構解決問題，讓課堂有一個旋律

聚焦本節課，自主性的學習設計、開放性的思辨場域、及時性的反思活動共同促成了學生的自主建構和思維爬坡。學生在與同伴對話、與教師對話、與教材對話、與自己對話的過程中不斷質疑、反思、辨析，透過表象，結合數位順序表認識到數學的本質，即小數點不會動，它是整數部分和小數部分的分界;它是數字的移動引發數的大小變化規律的關鍵點;人們為了表達方便稱這規律為“小數點搬家”;規律變化的根源是十進制;等等。不難發現，課堂上始終是學生在自主活動、主動對話、積極思辨，解決問題的過程就是他們自主建構的過程。

總之，教師要把握數學學習的本質，利用好學生的認知沖突和思維活動，要善于“把握學情，順學而導”，導在疑難時，導在關聯處，要以問導學、以問促學，實現“不教之教”。

（責編 金 鈴）