新三維離散系統的動力學及混沌控制

李德奎，魏興民

(1.甘肅中醫藥大學 定西校區 理科教學部，甘肅 定西743000；2.甘肅中醫藥大學 公共衛生學院，甘肅 蘭州730000)

0 引言

自1963年氣象學家Lorenz提出著名的Lorenz系統[1]以來，大量的混沌系統相繼被提出，其中具有代表性的連續系統有Chen系統[1]、Lü系統[1]等，離散系統有Logistic映射[2]、Hénon映射[2]等.對離散系統的研究目前主要集中在二維系統的動力學分析、同步控制及應用方面[3-7]，對高維離散系統的研究較少，然而現實生活中，利用高維離散系統能夠解決許多實際問題，尤其是在圖像加密中具有重要的應用價值[8-9]，為此研究高維離散系統的動力學及混沌行為是必要的.

混沌控制是混沌應用的前提.1990年，Ott等[10]提出了利用參數微擾法進行混沌控制，這種方法也被稱為是OGY方法，但是此方法的缺點是以局部線性化為基礎，控制過程中存在誤差.此后，混沌控制問題一直是混沌研究的一個熱點[11-16]，一些混沌控制方法被相關學者提出，例如自適應控制法[13]，滑膜控制法[14]，模糊邏輯控制法[15]，神經網絡控制法[16]，等等，這些方法為精確地實現混沌的控制與同步奠定了基礎.

基于以上考慮，本文基于Hénon映射為基礎，通過增加非線性項的方法，給出了一個三維離散系統，該系統共有12個項，其中含有7個非線性項，并研究了系統豐富的動力學行為，同時對系統的混沌行為利用Metican小波函數進行了控制，將系統的混沌運動控制到周期運動，本文的研究成果混沌遮掩保密通信技術具有重要的理論意義.

1 新三維離散系統

本文給出的新三維離散系統是一個三元二次迭代方程組，其動力學方程為

(1)

其中a、b為系統參數，取定參數b=0.3，當參數a∈[-0.3，0.4]時，繪制出系統(1)的分岔圖，并通過分岔圖分析系統的動力學行為，變量xn隨參數a變化的分岔圖如圖1所示.

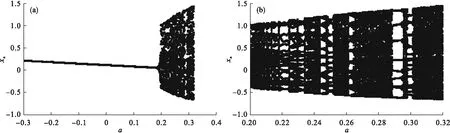
圖1 新離散系統(1)的分岔圖

從圖1(a)可以看出，當參數a∈[-0.3，0.2)時，系統(1)處于周期運動，當a∈[0.2，0.32]時，系統(1)進入混沌區域，從圖1(b)可以看出，在混沌區域內，有許多周期窗口，系統在混沌與周期運動之間交替運動.

取初值條件為x0=0.7，y0=0.3，z0=0.4，參數b=0.3時，給出了系統(1)在a的不同取值下的相圖.

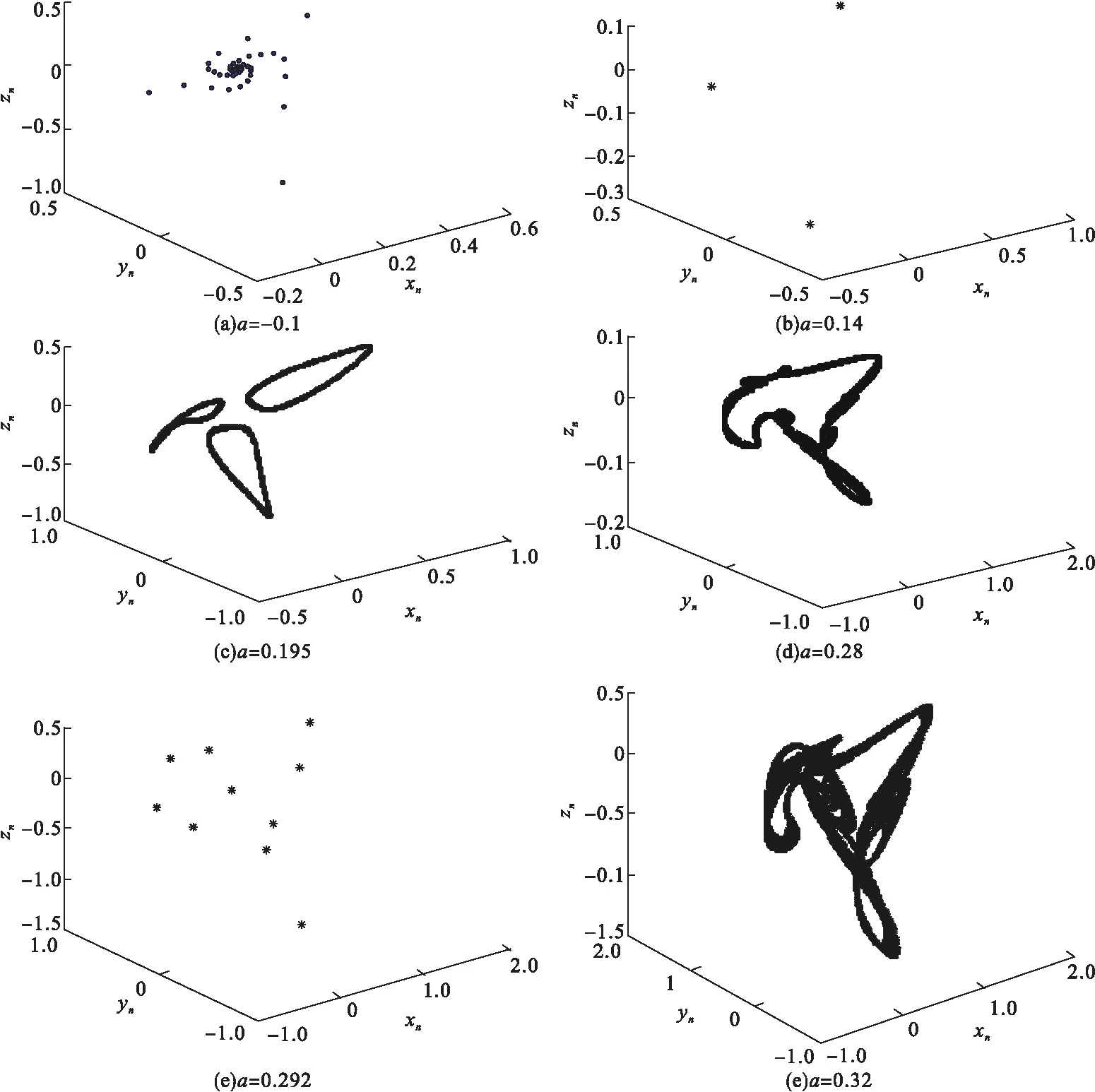
圖2 新離散系統(1)隨參數a變化的相圖

從圖2可以看出，當參數a=-0.1時，系統(1)穩定于平衡點，系統處于靜止狀態(如圖2(a)所示)；當參數a=0.14時，系統(1)穩定于周期三運動(如圖2(b)所示)；當參數a=0.195時，系統(1)的周期三失穩，出現三條閉合曲線(如圖2(c)所示)；當參數a=0.28時，系統(1)處于混沌運動狀態，具有如圖2(d)所示的混沌吸引子；當參數a=0.292時，系統(1)又處于周期十運動(如圖2(e)所示)，當參數a=0.32時，系統(1)處于混沌運動狀態，具有如圖2(f)所示的混沌吸引子.在混沌區內隨著參數a的不斷增大，周期運動與混沌運動交替出現，這與從圖1所示的分岔圖中得到的結論是一致的.

2 新三維系統的混沌運動

根據非線性系統的線性化方法，可得系統(1)的雅可比矩陣為

(2)

設

J=f′(x1)f′(x2)…f′(xi)

(3)

將矩陣J的3個特征值求模，得到由大到小的排列為

(4)

系統(1)的Lyapunov計算公式為

(5)

其中k=1，2，3.

根據系統(1)的Lyapunov計算公式為(5)，當系統參數a=0.32，b=0.3，初值條件為x0=0.7，y0=0.3，z0=0.4時，系統(1)的Lyapunov指數譜為(0.167 0，-0.410 0，-0.428 3)，有一個大于零的Lyapunov指數，說明系統(1)在參數a=0.32，b=0.3處于混沌運動狀態.

同樣在系統參數a=0.32，b=0.3時，針對兩組不同的初值條件x0=0.7，y0=0.3，z0=0.4和x0=0.700 01，y0=0.3，z0=0.4，考察系統對初值的敏感依賴性.

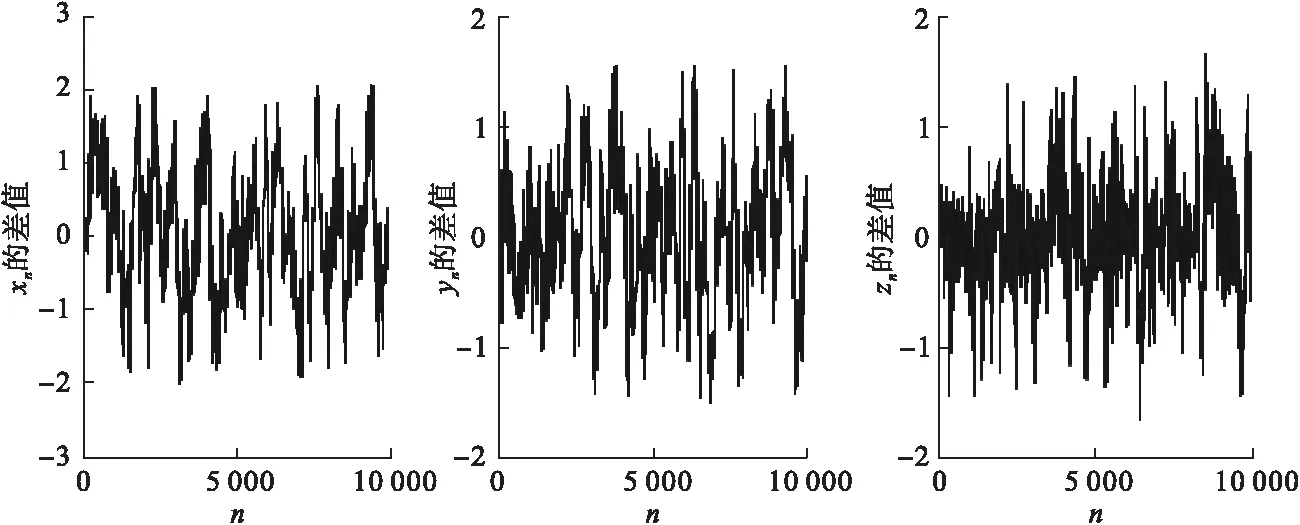
圖3 新離散混沌系統(1)對初值條件的敏感依賴性圖

從圖3可以看出，對于初值條件的微小差異，系統的運動軌跡大相徑庭，進一步說明當系統參數a=0.32，b=0.3時，系統(1)處于混沌運動狀態.

3 小波函數迭代控制

小波函數具有振蕩性，隨著自變量在正負方向的不斷延伸，小波函數快速衰減，因此其具有很強的收斂性，用小波函數進行混沌控制，能夠抑制系統的混沌行為，Metican小波函數的數學表達式為

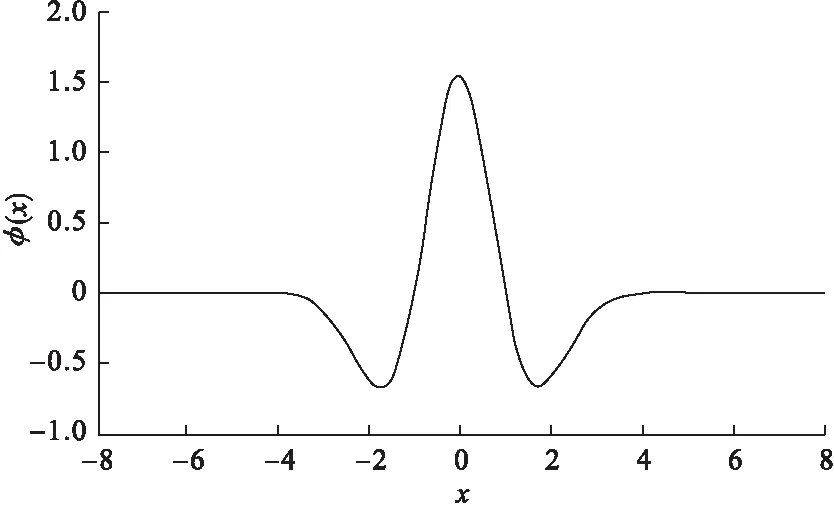
圖4 Metican小波函數的圖像

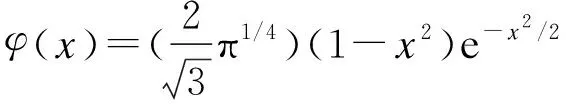
(6)

其圖像如圖4所示.Metican小波函數不具有正交性和尺度函數，但在時域和頻域上具有很好的局部化性質，同時滿足在全體實數區間上的無窮積分為零.

本文選擇Metican小波函數對系統(1)進行混沌控制，為了得到更多的控制結果，將小波函數的系數設為增益系數k，通過調節增益系數k的值，實現對系統(1)的各種控制，用小波函數分別乘以第一個和第二個方程，得到受控的迭代方程組為

(7)

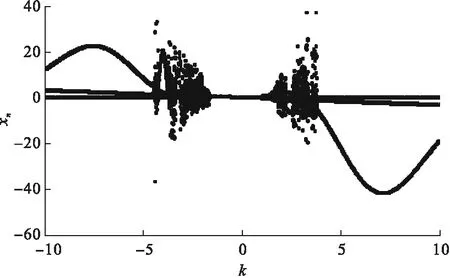
圖5 Metican小波函數控制下系統(1)分岔圖

將系統參數和初值條件取為a=0.32，b=0.3，x0=0.7，y0=0.3，z0=0.4時，系統(7)關于增益系數k的分岔圖如圖5所示.

從圖5可以看出，通過小波函數，可以將系統控制到周期軌道，同時也能將系統控制到混沌軌道等，可以看出當k=0.1時，小波函數能將系統控制到周期一運動，當k=5時，小波函數能將系統控制到周期三運動，當迭代次數n=2 000時，打開控制開關實施控制，小波函數控制的結果如圖6所示.

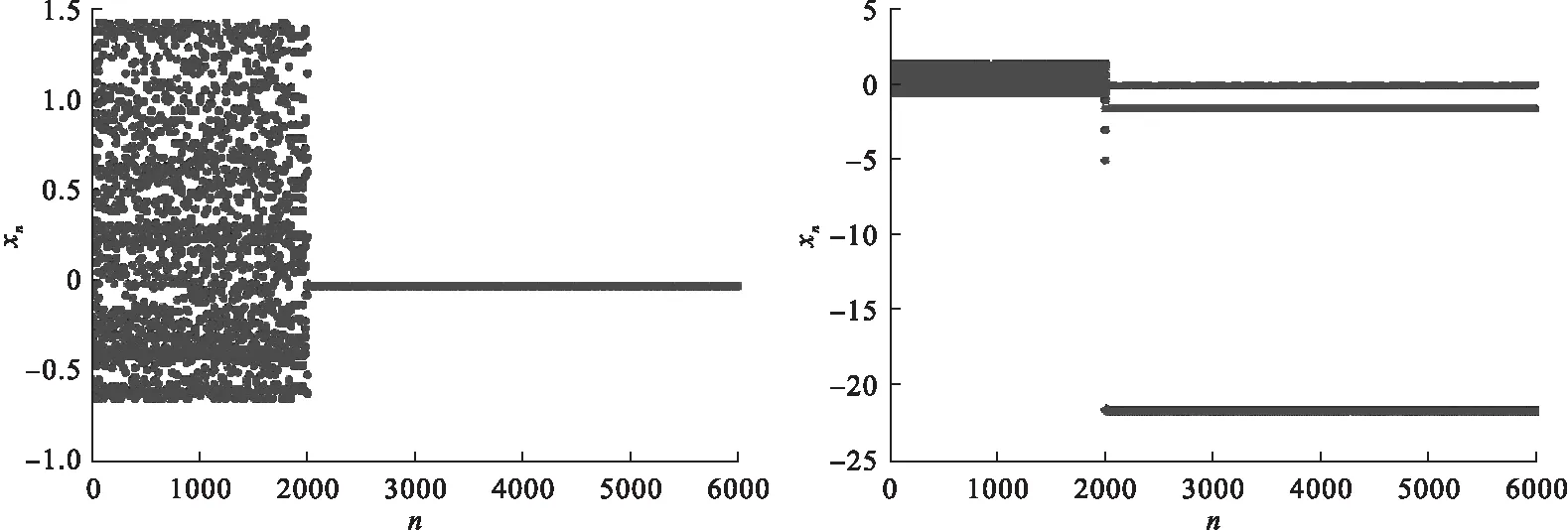
圖6 小波函數控制下系統(1)的迭代次數序列圖

4 結論

由于眾多實際問題能夠用高維離散系統來描述，所以研究高維離散系統的動力學行為及其混沌控制是非常必要的.本文給出的三維離散系統具有豐富的動力學行為：周期運動、準周期運動以及混沌運動等.通過Metican小波函數僅對三維離散系統的兩個變量進行了控制，在不同的反饋增益系數下，能將三維離散混沌系統控制到不同的周期軌道.