基于譜元法的車輛-軌道結構頻域振動特性研究

吳神花,雷曉燕

(華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，南昌 330013)

譜元法(SEM)是一種高精度的頻域分析方法[1]。該方法從動力偏微分方程出發，利用傅里葉變換將偏微分方程轉換為頻域內的常微分方程，通過引入相應的位移邊界條件和力邊界條件，得到單元譜剛度矩陣。再利用有限元思想，將整體結構離散為若干個單元，并將其組裝為整體結構譜剛度矩陣，最后利用虛擬激勵法模擬軌道不平順引起的虛擬激勵，通過求解整體結構的譜元法方程得到結構的振動響應。譜元法在結構離散時，單元尺寸的大小對中高頻振動計算精度影響甚微，能有效避免有限元法在網格劃分較細時帶來的計算效率低的問題，同時保持了有限元法對復雜結構適應性強的特點。目前，譜元法不僅可以分析固體結構振動問題[2-3]，還可以分析流體力學[4]中的問題，已成功應用于結構振動[5]、地震學[6]和結構損傷識別[7-8]等多個領域，是一種成熟的全頻域動力學分析方法，可以為車輛-軌道結構全頻域振動噪聲分析提供新思路。但將該方法應用于車輛-軌道結構頻域振動分析的研究,目前還沒有看到。

本文基于譜元法建立車輛-軌道結構頻域振動模型，將軌道結構模擬為三層鐵木辛柯梁，車輛部分考慮為整車模型，運用Lagrange方程實現車輛與軌道結構的耦合，并運用虛擬激勵法將軌道不平順模擬為虛擬荷載，最后通過求解整體結構的譜元法方程得到車輛-軌道結構全頻域振動響應。

1 基于譜元法的車輛-軌道結構振動分析方法

1.1 軌道結構模型

軌道結構模擬為三層鐵木辛柯梁單元，如圖1所示。其中，鋼軌、預制軌道板和混凝土支撐層分別離散為黏彈性點支撐的二維鐵木辛柯梁譜單元，鋼軌扣件由離散分布的彈簧-阻尼單元模擬，CA砂漿和路基由均布的彈簧-阻尼單元模擬。

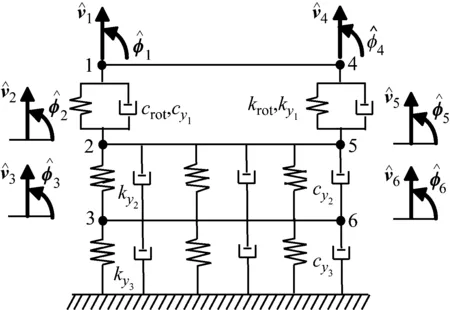
圖1 無砟軌道結構三層梁譜單元法模型Fig.1 Three layer beam model of ballastless track structure

定義無砟軌道結構三層梁單元的譜結點位移向量為

1.1.1 Timoshenko梁單元譜剛度矩陣

自由振動的Timoshenko梁運動微分方程如下

(1)

式中:G為剪切彈性模量;κ為剪切因子;E為彈性模量;I為橫截面的慣性矩;ρ為材料密度;A為梁截面面積;v為梁的垂向位移;φ為彎曲引起的轉角。

將垂向位移和轉角表示為譜分量的形式

(2)

由式(1)和(2)可得

(3)

設式(3)的一般解為

(4)

將式(4)代入式(3)可以求出波數四個解

(5)

其中：

式(4)的解可表示為

(6)

式(6)前兩項表示向右傳播的波，后兩項表示向左傳播的波，l為梁單元長度，其中：

A，B，C，D為待定系數，可通過引入位移邊界條件求得，位移邊界條件如圖2所示。

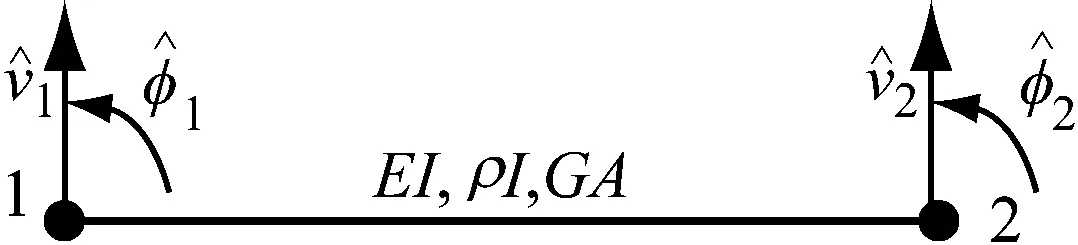
圖2 鐵木辛柯梁單元邊界位移Fig.2 Boundary displacement of Timoshenko beam element

(7)

通過式(6)和(7)可以求得

(8)

其中

將式(8)代入式(6)可得

(9)

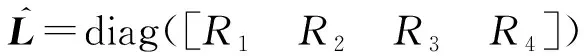
鐵木辛柯梁內部彎矩和剪力可以表示為

(10)

將荷載表示為譜分量的形式

(11)

引入鐵木辛科梁梁端荷載邊界如圖3所示。

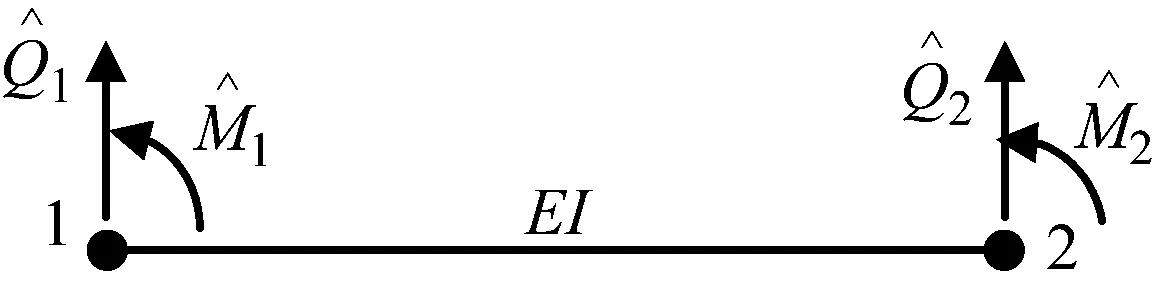
圖3 鐵木辛科梁邊界荷載Fig.3 Boundary load of Timoshenko beam

(12)

其中S(ω)為鐵木辛柯梁譜單元剛度矩陣，可表示為

(13)

其中：

1.1.2 彈簧-阻尼單元譜剛度矩陣

s2=k2+ic2

(14)

式中：k2，c2分別為無砟軌道單元彈簧-阻尼剛度矩陣和阻尼矩陣，公式見參考文獻[9]；s2為軌道結構彈簧-阻尼單元譜剛度矩陣。

1.1.3 整體譜剛度矩陣

將鋼軌、預制軌道板、混凝土支撐層譜單元剛度矩陣以及彈簧-阻尼單元譜剛度矩陣采取對號入座的方式，組裝為軌道結構整體譜剛度矩陣Sl(ω)。

1.2 車輛模型

車輛部分模擬為整車模型，車體和轉向架考慮沉浮振動和點頭振動，車輪考慮沉浮振動，每節鋼軌上兩個節點考慮豎向位移和轉角，整車模型有26個自由度，如圖4所示。

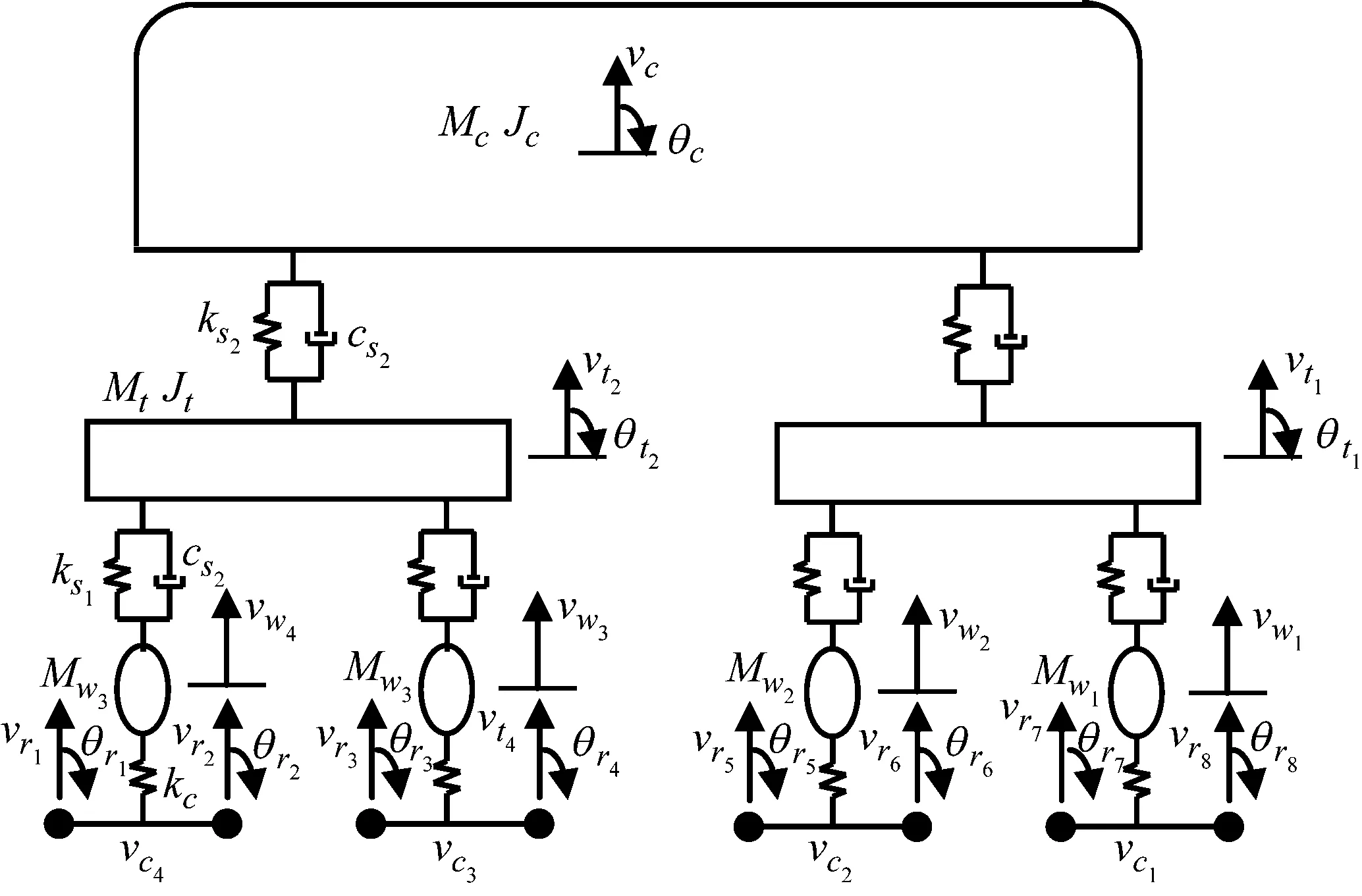
圖4 整車車輛單元模型Fig.4 Vehicle model

圖4中：vci(i=1,2,3,4)為第i個輪軌接觸處鋼軌豎向位移；vi(i=r1,r2,r3,…,r8)分別表示鋼軌第i個節點的垂向位移；θi(i=r1,r2,r3,…,r8)表示鋼軌第i個節點的轉角。

車輛單元的節點位移向量au,e可以表示為

au,e={vr1θr1vr2θr2vr3θr3vr4θr4vr5θr5vr6θr6vr7θr7vr8θr8θr8vcθcvt1vt2vw1vw2vw3vw4}T

(15)

運用Lagrange方程，可得車輛方程

Muau+Cuau+Kuau=Qu+Qη

(16)

式中：Mu，Cu，Ku分別為車輛單元的剛度、阻尼和質量矩陣;Qu為車輛重力荷載列向量，Qη為軌道不平順激勵，公式如下

(17)

式中:kc為輪軌接觸剛度；Nc1,Nc2,Nc3,Nc4為插值矩陣；η1，η2，η3，η4為軌道不平順，將通過虛擬激勵法來模擬。

設不平順η(t)的功率譜密度函數為Sη(ω)，則相應的軌道不平順虛擬激勵為

(18)

由于軌道不平順功率譜是以空間圓頻率表示的單邊功率譜，而Sη(ω)為時間功率譜，因此需先將軌道不平順功率譜轉換，時間圓頻率ω=βv，β為空間圓頻率，v為列車速度，則時間功率譜Sη(ω)為

Sη(ω)=Sη(β)/v

(19)

對于M個輪對情況，有

(20)

式中:η(t)為軌道高低不平順隨機激勵歷程函數;tj(j=1,2,…M)為各激勵點處的激勵滯后時間，tj=(aj-a1)/v,aj為t=0時第j個車輪的位置坐標。

與η(t-tj)相應的軌道不平順虛擬激勵為

(21)

對于M個輪對作用情況，式(20)表示為

(22)

其中：

(23)

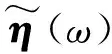
僅考慮由于軌道不平順引起的激勵，式(16)可變為

Muau+Cuau+Kuau=Qη

(24)

由于軌道高低不平順為虛擬激勵，與此相應的位移響應為

(25)

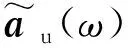
將式(17)、(22)和(25)代入式(24)可得

(26)

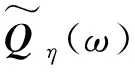
(27)

Su(ω)=(ω2Mu+iωCu+Ku)

(28)

1.3 求解車輛-軌道結構振動響應譜元法方程

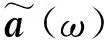
(29)

根據虛擬激勵法原理，系統結點位移的實際功率譜密度S(ω)為

(30)

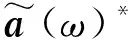
(31)

2 基于譜元法的車輛-軌道結構振動頻域分析

采用德國高低不平順低干擾譜作為軌道不平順激勵，列車速度為250 km/h，線路長度為200 m，軌道單元長度為0.65 m，列車參數和軌道結構參數分別見表1和表2。

2.1 模型驗證

圖5為0.2～200 Hz內的車體、轉向架、車輪垂向加速度功率譜，車體、轉向架沉浮加速度的自振頻率分別為1 Hz和7.6 Hz，按參考文獻[10]公式算出的車體、轉向架沉浮加速度的自振頻率分別為1.08 Hz和7.9 Hz，可見本文計算結果與參考文獻計算結果吻合良好。圖5中車體、轉向架加速度功率譜谷值處分別對應車輛“定距濾波”和“軸距濾波”頻率，與參考文獻[11]公式得到的“定距濾波”和“軸距濾波”頻率吻合良好，證明了基于譜元法的車輛-軌道結構振動頻域分析方法的正確性。

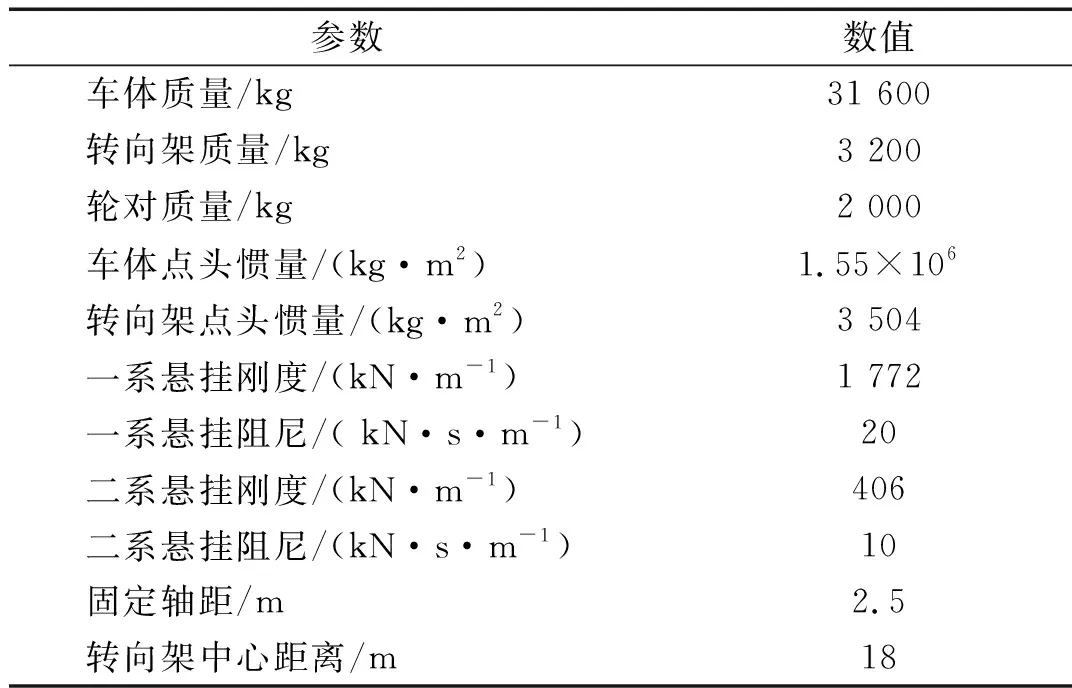
表1 無砟軌道結構參數

表2 高速列車參數

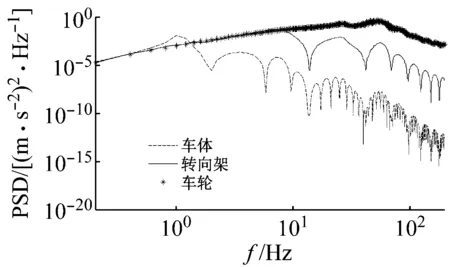
圖5 車輛沉浮加速度功率譜

2.2 基于譜元法的車輛-軌道結構振動頻域分析

為了得到軌道結構系統的自振頻率，不考慮車輛部分，在三層軌道結構系統中間施加一個單位簡諧荷載，得到鋼軌、軌道板、底座板的垂向位移導納，如圖6所示。由圖6可知,鋼軌第一、第二階自振頻率為30 Hz、250 Hz，鋼軌一階pinned-pinned頻率為1 062 Hz；軌道板和底座板的第一、第二、第三、第四階自振頻率為30 Hz、508 Hz、1 000 Hz、2 839 Hz。

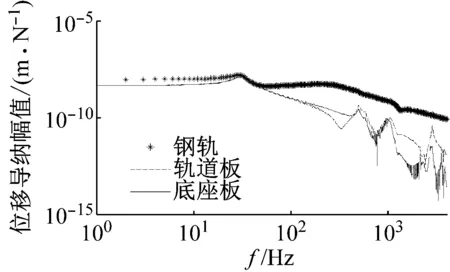
圖6 軌道結構垂向位移導納Fig.6 Vertical displacement admittance of track structure

基于譜元法的車輛-軌道結構振動模型，考慮軌道結構單元尺寸為0.650 0 m、0.375 0 m、0.187 5 m的三種工況，分析車輛-軌道結構頻域振動特性。計算結果表明,三種工況下得到的頻域振動響應相同，軌道結構單元尺寸大小不會影響計算精度，可見譜元法分析軌道結構中高頻振動比有限元法更具優勢。以下分析的單元尺寸均為0.650 0 m，圖7和8分別為分析頻率0.2～200 Hz、1～4 000 Hz內軌道結構垂向加速度功率譜曲線，圖9為分析頻率1～4 000 Hz內的車輛垂向加速度功率譜曲線。

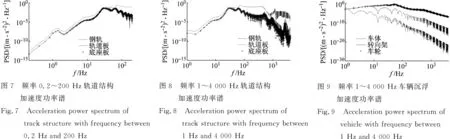
如圖7所示，鋼軌、軌道板、底座板的前2階振動峰值頻率為1.1 Hz和8 Hz，分別對應圖5中車體、轉向架的自振頻率；鋼軌、軌道板、底座板的第三階振動峰值頻率為28 Hz，對應圖6中鋼軌、軌道板、底座板的一階自振頻率；鋼軌、軌道板、底座板的第四階峰值頻率對應圖5中車輪自振頻率。綜上可見,鋼軌、軌道板、底座板前2階振動峰值由車體、轉向架自振產生，第三階峰值頻率由軌道結構系統自振產生，第四階峰值頻率由車輪自振產生。

由圖8可知，鋼軌、軌道板和底座板的振動在28 Hz、504 Hz和2 660 Hz處有峰值，分別對應圖6中軌道結構系統一階自振頻率、軌道板和底座板的第二、第四階自振頻率，說明軌道結構系統的這幾處峰值都是由軌道結構系統自振引起的；而鋼軌另一處峰值在1 166 Hz處，軌道板和底座板在922 Hz處，這也是對應圖6中軌道板第三階自振頻率，可見此處峰值是由軌道結構系統自振產生的，而鋼軌、軌道板和底座板的峰值頻率之間的差異是由于圖6中鋼軌的pinned-pinned振動導致的。

由圖8還可以看到，在全頻域內鋼軌振動遠遠大于軌道板和底座板的振動，說明鋼軌扣件在全頻域內具有良好的減振效果；在頻率小于500 Hz時，軌道板和底座板加速度功率譜相同，說明小于500 Hz時，CA砂漿無減振作用；但大于500 Hz時，軌道板振動遠大于底座板的振動，說明高頻振動衰減快。

由圖9可知，車體和轉向架的加速度功率譜對應的谷值處頻率符合“車輛幾何濾波效應，由圖9可見,轉向架的自振頻率為7.6 Hz，當頻率大于轉向架自振頻率時，車輪振動大于車體和轉向架的振動，說明一、二系懸掛減振具有良好的效果。在頻率為500 Hz時，車輪的加速度功率譜也有峰值，與下部軌道結構對應的峰值頻率相同，說明該峰值也是由軌道結構系統自振引起的。

2.3 輪軌接觸處車輛-軌道結構系統的振動響應

車輛-輪軌耦合系統包含了一節車廂四個輪軌接觸激勵，圖10和11分別為四個車輪作用處車輪、鋼軌加速度功率譜曲線。

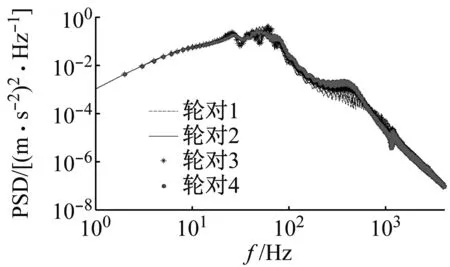
圖10 四個車輪加速度功率譜Fig.10 Acceleration power spectrum of four wheels

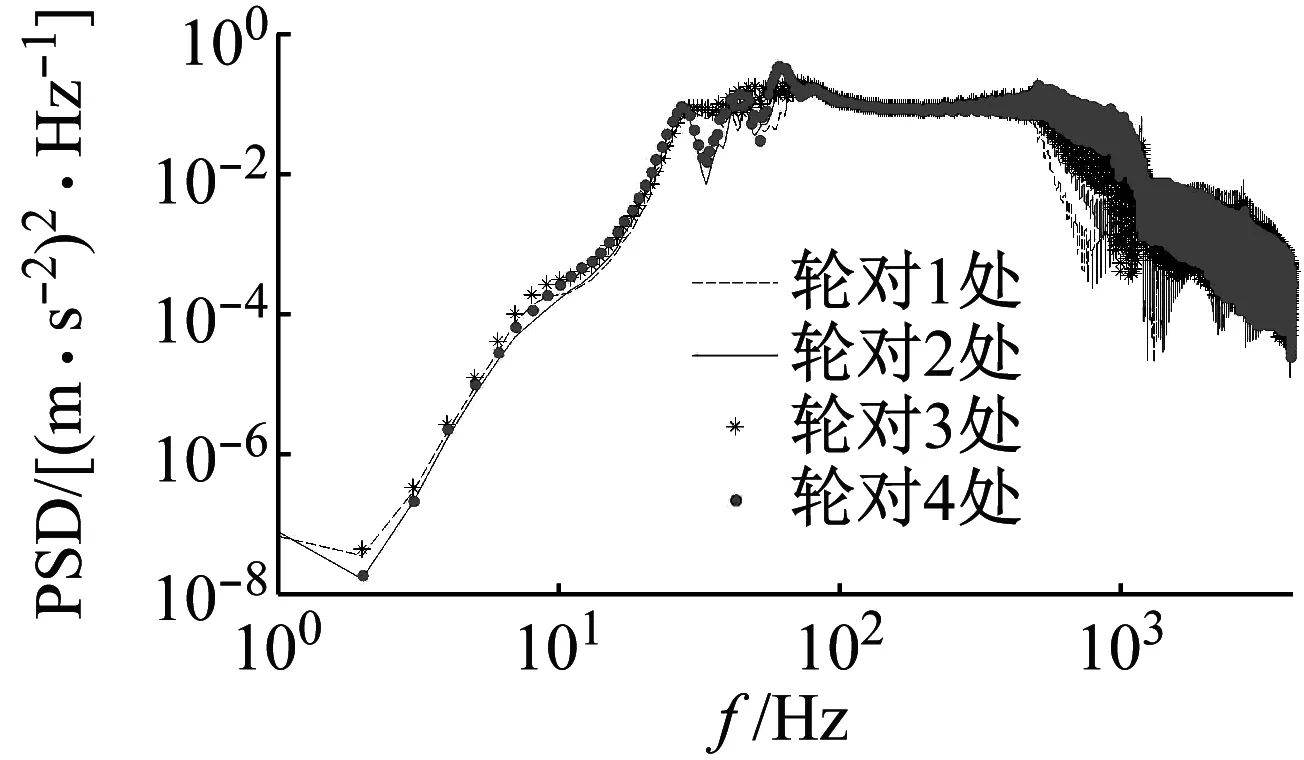
圖11 四個輪對處鋼軌加速度功率譜Fig.11 Acceleration power spectrum of rail at four wheelsets

由圖10可知：在小于25 Hz、大于1 000 Hz和80～1 000 Hz內，四個車輪振動相同；在20～80 Hz內，四個車輪峰值不同；在120～500 Hz內，車輪4振動最大，在400～1 000 Hz內，車輪1振動最大；四個車輪均在500 Hz處有峰值，這是由軌道結構系統自振引起。

由圖11可知，在小于25 Hz和80～500 Hz內，鋼軌振動在四個輪對作用處振動相差不大；在25～80 Hz內，鋼軌的振動峰值有差異，與圖10對應車輪振動峰值相同，說明該頻域內主要受車輪自振的影響較大；在500～1 000 Hz內，鋼軌振動大小關系為：車輪4處>車輪3處>車輪2處>車輪1處；大于1 000 Hz時，鋼軌振動大小關系為：車輪4處<車輪3處<車輪2處<車輪1處。

2.4 遠離車輛一側沿鋼軌方向軌道結構振動響應

圖12和13為遠離車輛一側且距離端輪對0、2.5 m、18.0 m、20.5 m處鋼軌、軌道板振動加速度功率譜曲線。由圖12可知，在距離端輪對2.5 m處，1～800 Hz內鋼軌振動迅速衰減,當大于800 Hz時，鋼軌振動衰減不大；在距離端輪對18.0 m與20.5 m處，25～1 171 Hz內的鋼軌振動基本相同，說明距離端輪對18.0 m處，鋼軌振動衰減基本穩定；在距離端輪對20.5 m處，小于25 Hz時，鋼軌振動隨著離開端輪對距離的增加迅速衰減，衰減幅值超過了103倍，當大于1 171 Hz時鋼軌振動則衰減較小。由圖13可知:在1～25 Hz與500～2 000 Hz內軌道板振動距端輪對越遠而衰減越大;在25～500 Hz和大于2 000 Hz內，軌道板振動衰減甚微，基本趨于穩定。

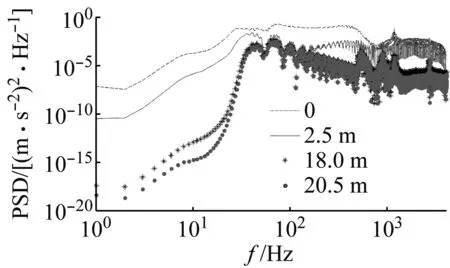
圖12 鋼軌加速度功率譜Fig.12 Acceleration power spectrum of rail

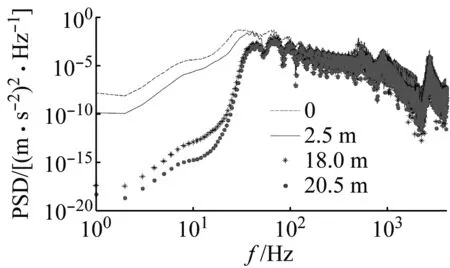
圖13 軌道板加速度功率譜Fig.13 Acceleration power spectrum of track plate

3 結 論

本文基于譜元法建立了車輛-軌道結構振動頻域分析模型，運用虛擬激勵法將軌道不平順模擬為虛擬荷載，運用Lagrange方程實現車輛與軌道結構的耦合，從而建立車輛-軌道結構的整體譜元法方程。利用該方法，分析了車輛-軌道結構在頻域內的振動響應，得到以下結論：

(1) 鋼軌、軌道板和底座板的第一、第二、第四階振動峰值分別由車體、轉向架、車輪自振引起；其他振動峰值由軌道結構系統自振引起。鋼軌、軌道板和底座板的振動能量分布在較寬的頻率范圍。

(2) 鋼軌扣件在全頻域內具有良好的減振效果；由于CA砂漿的剛度比較大，CA砂漿層對軌道結構的減振作用不明顯。

(3) 遠離車輛一側且距離端輪對2.5 m處，1～800 Hz內鋼軌振動迅速衰減,當大于800 Hz時，鋼軌振動衰減不大；在距離端輪對18.0 m處，25～1 171 Hz內的鋼軌振動衰減基本穩定；在距離端輪對20.5 m處，小于25 Hz時，鋼軌振動隨著離開端輪對距離的增加迅速衰減，衰減幅值超過了103倍，當大于1 171 Hz時,鋼軌振動則衰減較小；在1～25 Hz與500～2 000 Hz內，軌道板振動距端輪對越遠衰減越大。

(4) 基于譜元法的車輛-軌道結構振動分析方法具有計算速度快、計算精度高的特點，為車輛-軌道耦合系統結構振動全頻域分析提供了一種新方法。