預應力管樁動測承載力數值分析及參數取值研究

陳榮保，張季超，陳澤宇，顧美湘

(1. 廣州大學 土木工程學院，廣州 510006； 2. 佛山市禪城區建設工程質量安全檢測站，廣東 佛山 528000)

Bowles[1-2]對基樁錘擊時的動力性能進行了分析，采用有限差分式代替描述沖擊波沿樁身傳播的微分方程，并采用計算機進行運算，從而推進了波動方程在打樁分析中的應用。Liang等[3]研究了一種一維波動方程的算法，通過對大量測試數據的分析，估算了樁端阻力和樁側阻力，求得了波動方程的封閉形式解，從而推定出樁側和樁端阻尼系數和靜土阻力。陳久照等[4]采用連續桿件模型，基于一維行波理論，建立了研究高應變動力試樁的數值計算模型與算法，根據數值分析的結果定量評價了重錘激發樁側土阻力及樁端土阻力的能力和高應變動力試樁中各因素對承載力的影響。Svinkin等[5]強調對于基樁動測承載力的計算，應該著重確定工程上的應用領域和研究，才可提高動力試樁的可靠性。楊志琛[6]通過對大量高應變測試結果和靜載試驗結果對比分析，總結出高應變法和靜載法的關系，推定出在各種地質條件下各種樁型的CASE阻尼系數的取值范圍。劉士偉[7]對樁側土最大彈性變形值和樁底土最大彈性變形值兩個動力參數的取值問題進行了討論，通過工程實例中十幾支樁的動靜對比試驗來驗證高應變法的測試結果，并驗證了確定的樁側土最大彈性變形值和樁底土最大彈性變形值取值的合理性。賀曉華[8]對基樁動測承載力計算公式進行了分析，并考慮樁側阻尼的影響和根據樁側土阻力將使應力波發生指數衰減的規律，對CASE法承載力計算公式進行了改進。李颯等[9]基于可靠性原理，對不同樁徑以及不同樁長的混凝土預制樁的高應變測試結果與靜載試驗數據結果進行了分析，研究了預應力管樁高應變動力測試值與其靜載試驗值的相關性。Salgado等[10]結合實際工程，采用一種先進的動力沉樁分析模型，以建立精確的打樁計算公式，經與靜載試驗結果相比，表明該公式計算結果較為合理。熊凱峰等[11]進行了強風化泥質粉砂巖預應力管樁高應變動力測試和動力參數取值的研究，研究成果表明12根試驗樁高應變測試和靜載試驗結果的豎向承載力偏差在±15%范圍內。此外，關于樁基的動力特性，王奎華等[12]對三維波動土中帶承臺單樁的縱向振動特性進行了研究；吳文兵等[13]對任意層地基中黏彈性楔形樁的縱向振動特性進行了研究；鄭長杰等[14]對考慮土體三維波動效應的現澆大直徑管樁縱向振動頻域特性進行了研究。

雖然以上諸多學者對基樁動測承載力理論計算公式進行了研究和分析，但仍存在以下問題：① 樁周土動力參數取值時，未考慮與其埋深的關系；② 所涉及基樁動測承載力理論計算分析時，各樁側土層動力參數阻尼系數和最大彈性變形值未根據土層性質分別取值進行計算，其動力學計算模型與實際情況不相符合，導致計算結果存在一定的偏差；③ 相關靜動對比的試驗樁，大多數采用工程樁進行試驗，所進行的靜載試驗不是極限荷載試驗，此時土阻力未充分激發，在此情況下以靜載試驗結果來分析基樁動測承載力的準確性不太合理。

針對以上存在的問題，通過樁周土動三軸室內試驗，分析土層埋深對高應變錘擊樁時土動力學響應的影響規律；各土層采用不同阻尼系數和最大彈性變形值，以及樁側阻力采用非線性分布方式，對Bowles方法進行改進，使基樁動測承載力理論計算更適合實際情況；對全部試驗樁進行極限荷載試驗，以此驗證基樁動測承載力計算改進方法。

本文研究成果對預應力管樁動測承載力理論計算具有指導作用和對實際工程高應變測試時具有參考價值。

1 試驗場地概況

試驗場地樁端持力層為強風化泥質粉砂巖。共布置12根高強混凝土預應力管樁，其中φ500(壁厚125 mm)共10根，φ400(壁厚95 mm)共2根，樁間距為8 m。對每根樁進行地質勘察，鉆探孔中心離管樁孔中心為0.8 m，其中10號樁地層勘察情況見表1，其它試驗樁地層分布情況與10號樁相接近，但各地層層厚和層底埋深有所不同。其中7、8、9、10、11號樁共五根樁預埋滑動測微計，以測試各級荷載下樁身應變和內力，并計算樁側阻力、樁端阻力及樁端位移。各試驗樁基本情況見表2。

表1 10#樁地質勘察情況

表2 試驗樁基本情況

2 樁周土動三軸室內試驗及分析

2.1 概況

試驗采用美國SPAX-2000(改進型)靜動真三軸測試儀，針對該試驗場地七種樁周土類，取其中四種典型土類進行不同固結比下的動強度、動模量與阻尼比以及應力應變關系測試。根據預應力管樁高應變試驗條件，本次利用單向振動三軸方式進行振動試驗，試驗工作量統計見表3。

表3 動三軸試驗工作量統計

2.2 試驗數據整理及分析

在給定試驗條件下，對試驗數據進行整理及分析，其中動模量和阻尼比計算如下

動模量Ed=動應力增量/相應動應變增量。可分為四種動模量：初始模量、加載平均模量、加載最大模量和卸載模量。

阻尼比λd則由下列所測動態應力應變關系表所示的應力滯回圈，按以下關系式直接計算

λd=A/(4πAS)

(1)

式中：A為滯回圈 ABCDA 的面積，cm2，見圖1；AS為三角形 OAE 的面積，cm2。

(1) 粉質黏性土動三軸數據處理及分析

粉質黏性土動三軸試驗條件與數據處理及分析如圖2～圖4和表4～表9所示。

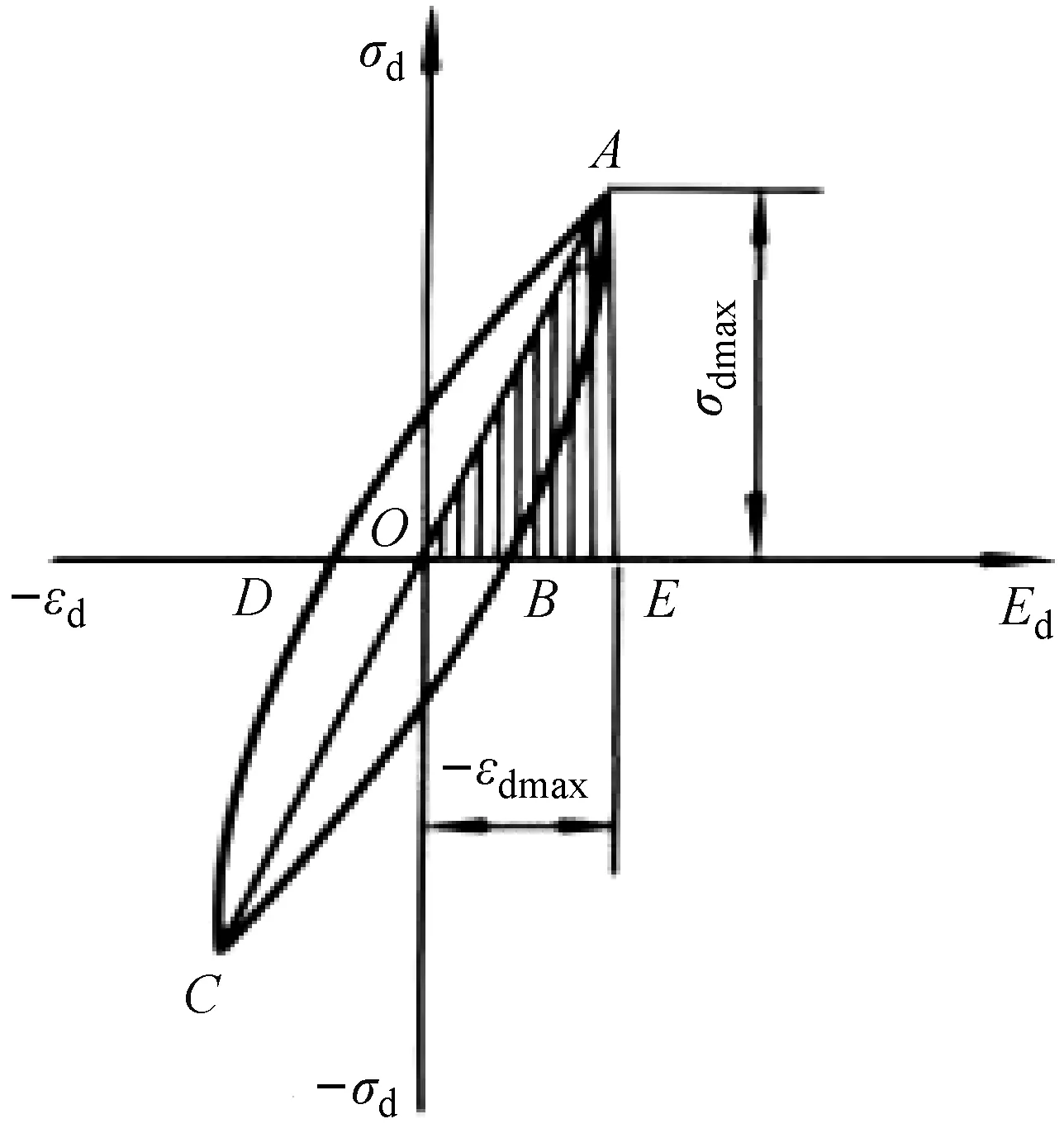
圖1 應力-應變滯回曲線Fig.1 Stress-strain hysteresis loop

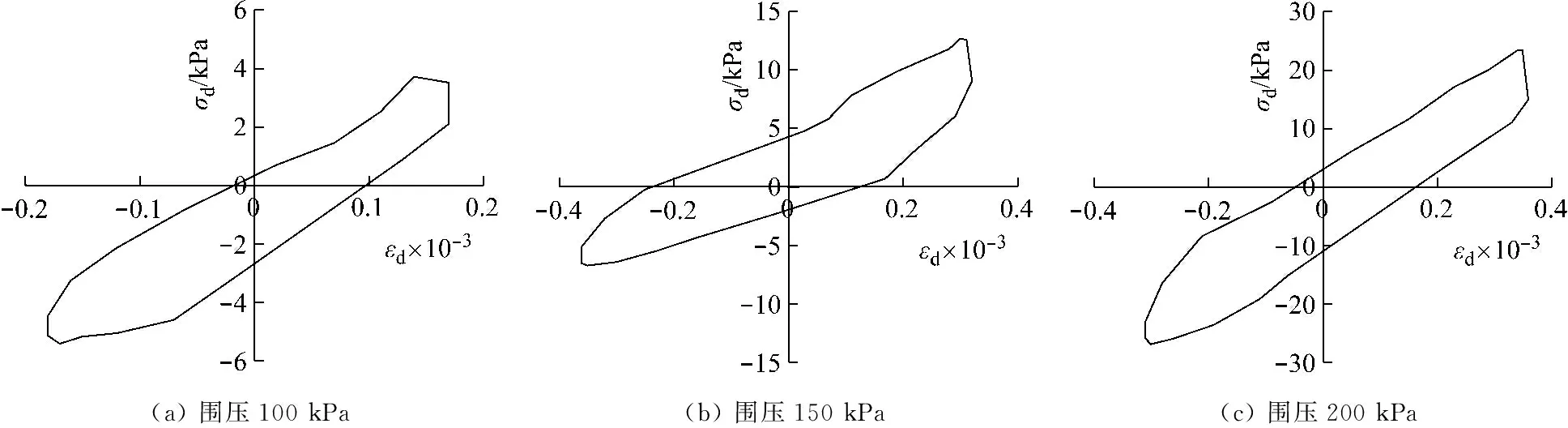
圖2 第一組粉質黏土應力-應變滯回圈

表4 第一組粉質黏土阻尼比

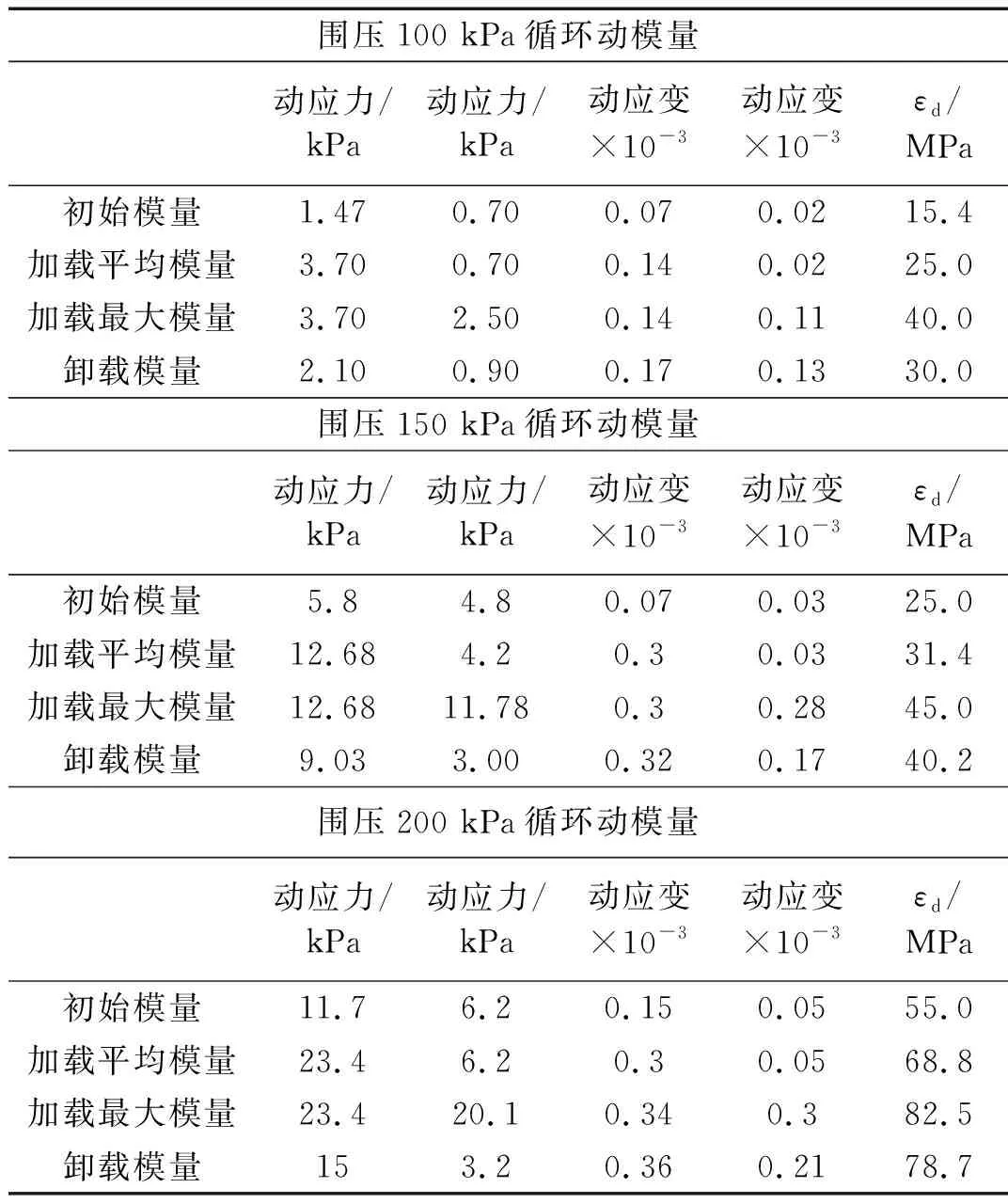
表5 第一組粉質黏土動模量

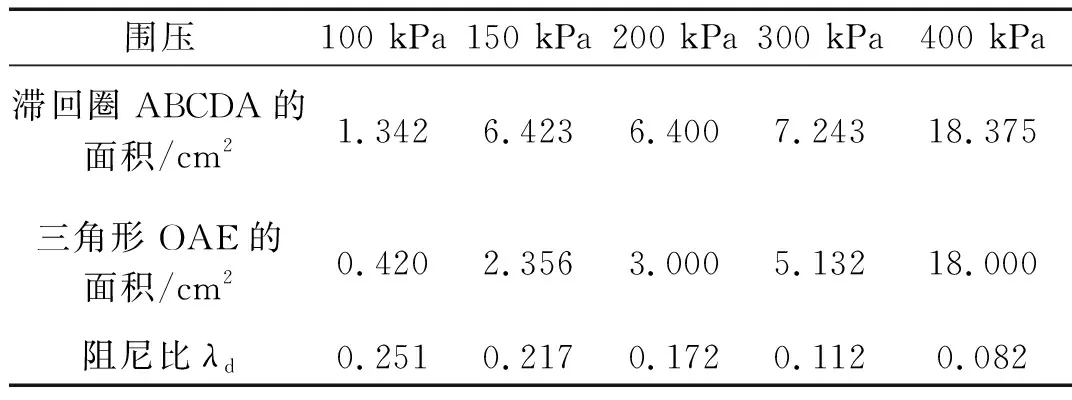
表6 第二組粉質黏土阻尼比

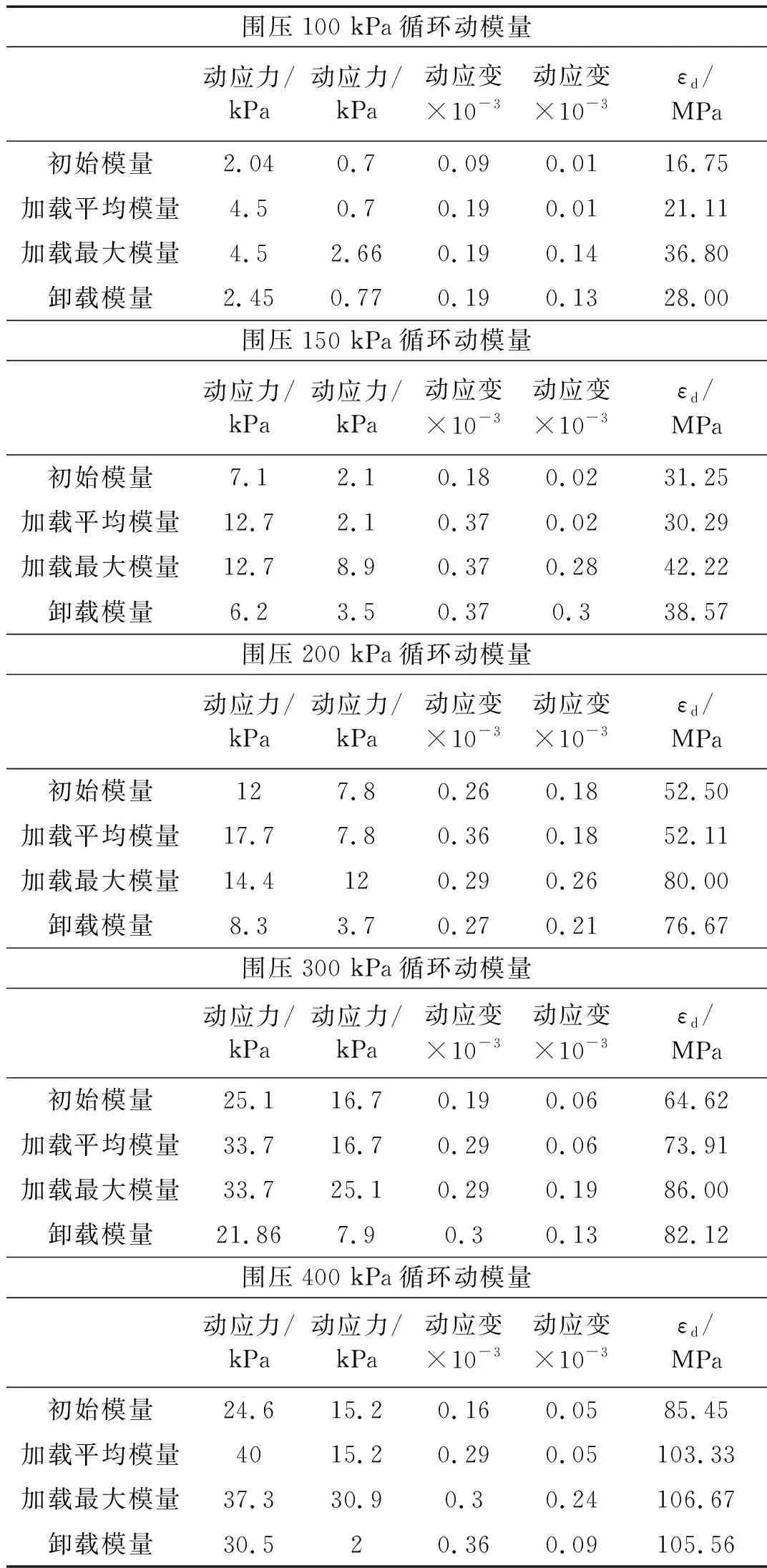
表7 第二組粉質黏土動模量

(a) 圍壓100 kPa(b) 圍壓150 kPa(c) 圍壓200 kPa

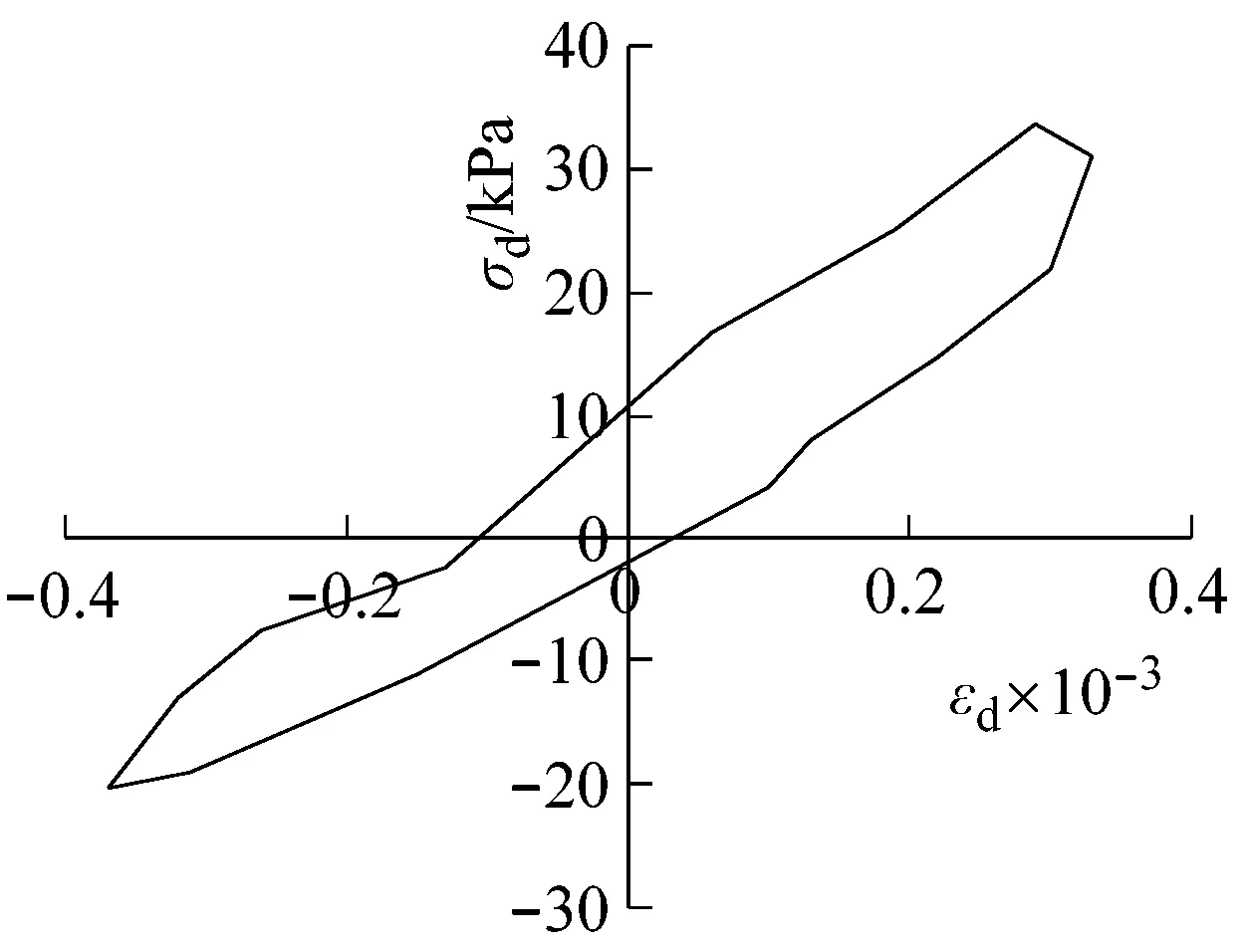
(d) 圍壓300 kPa(e) 圍壓400 kPa圖3 第二組粉質黏土應力-應變滯回圈Fig.3 Stress-strain hysteresis loops of the second group of silty clay

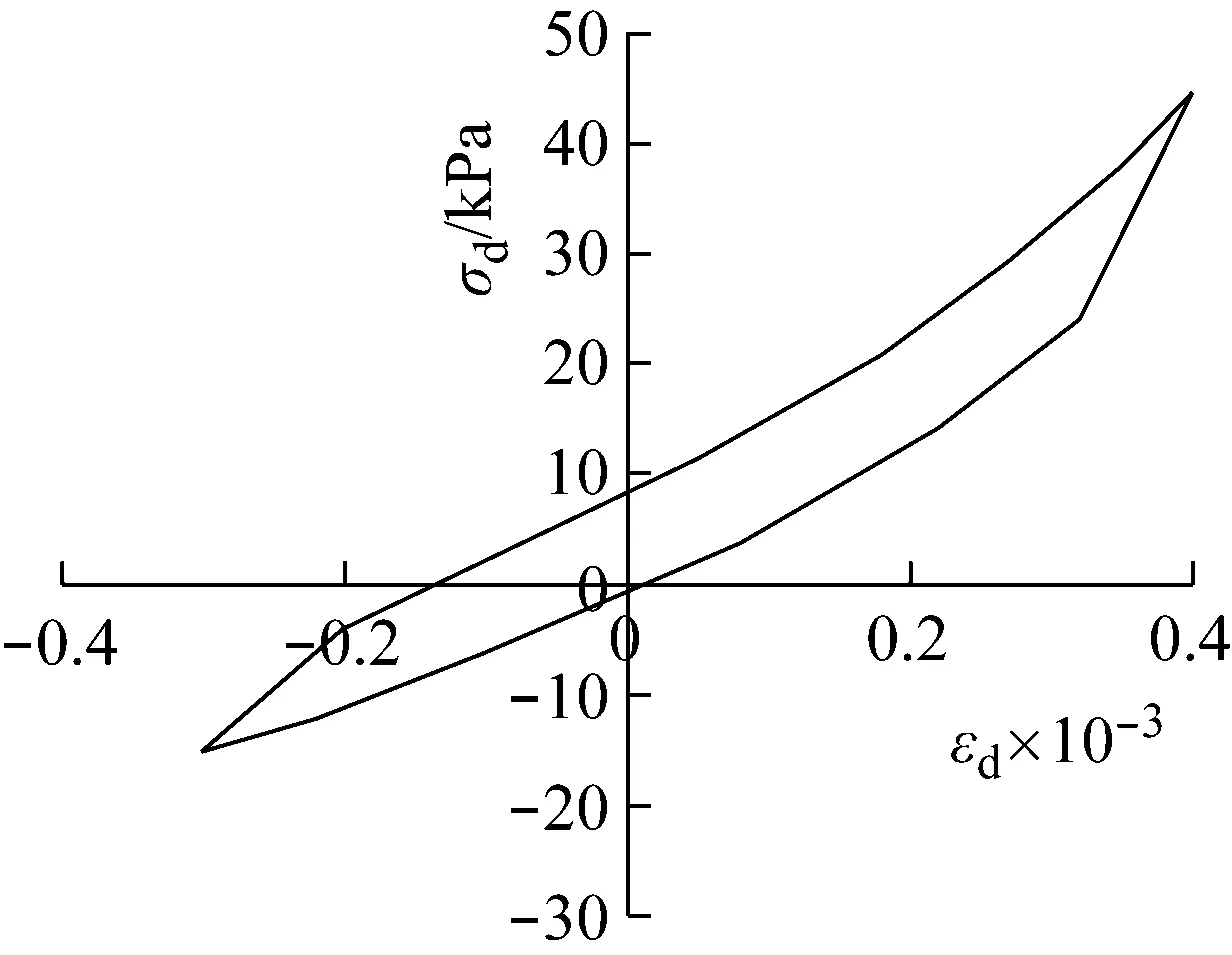
(a) 圍壓300 kPa(b) 圍壓350 kPa(c) 圍壓400 kPa圖4 第三組粉質黏土應力-應變滯回圈Fig.4 Stress-strain hysteresis loops of the third group of silty clay

表8 第三組粉質黏土阻尼比

由阻尼比計算表(表4、6、8)可見，在圍壓100～200 kPa范圍內，阻尼比λd則由0.245逐漸變小為0.171；在圍壓100～400 kPa范圍內，阻尼比λd則由0.251逐漸變小為0.082；在圍壓300～400 kPa范圍內，阻尼比λd則由0.110逐漸變小為0.080。此外，同一試驗條件下不同滯回圈相應阻尼比比較顯示，200 kPa及以下圍壓下，各次動應力應變循環的阻尼比變化很小，隨著圍壓增大阻尼比則有所下降。由動模量計算表(表5、7、9)可見，各種動變形模量隨圍壓增加均有明顯增加。試驗結果表明：

① 樁埋深較淺處，土阻尼消耗傳遞錘擊能量較大，故土層分布尤其是較淺部土層分布對高應變錘擊樁時土動力學響應影響較大。

② 隨著樁埋深增加，同種土的阻尼比會隨著下降，即隨著樁埋深增加，同種土的樁側阻尼系數會隨著下降，故土層較深時樁側阻尼系數在取值范圍內宜取小值。

(2) 淤泥質土、淤泥和全風化泥質粉砂巖動三軸數據處理及分析

圖2、圖4和表4～表9顯示了粉質黏土試驗量具體量值及變化，淤泥質土、泥巖和全風化泥質粉砂巖各試驗量具體量值不同于粉質黏土，但相關規律與前述粉質黏土相應規律相同。

3 試驗樁數值分析和計算結果

3.1 力學模型建立

3.1.1 樁力學模型和樁頂附屬設備

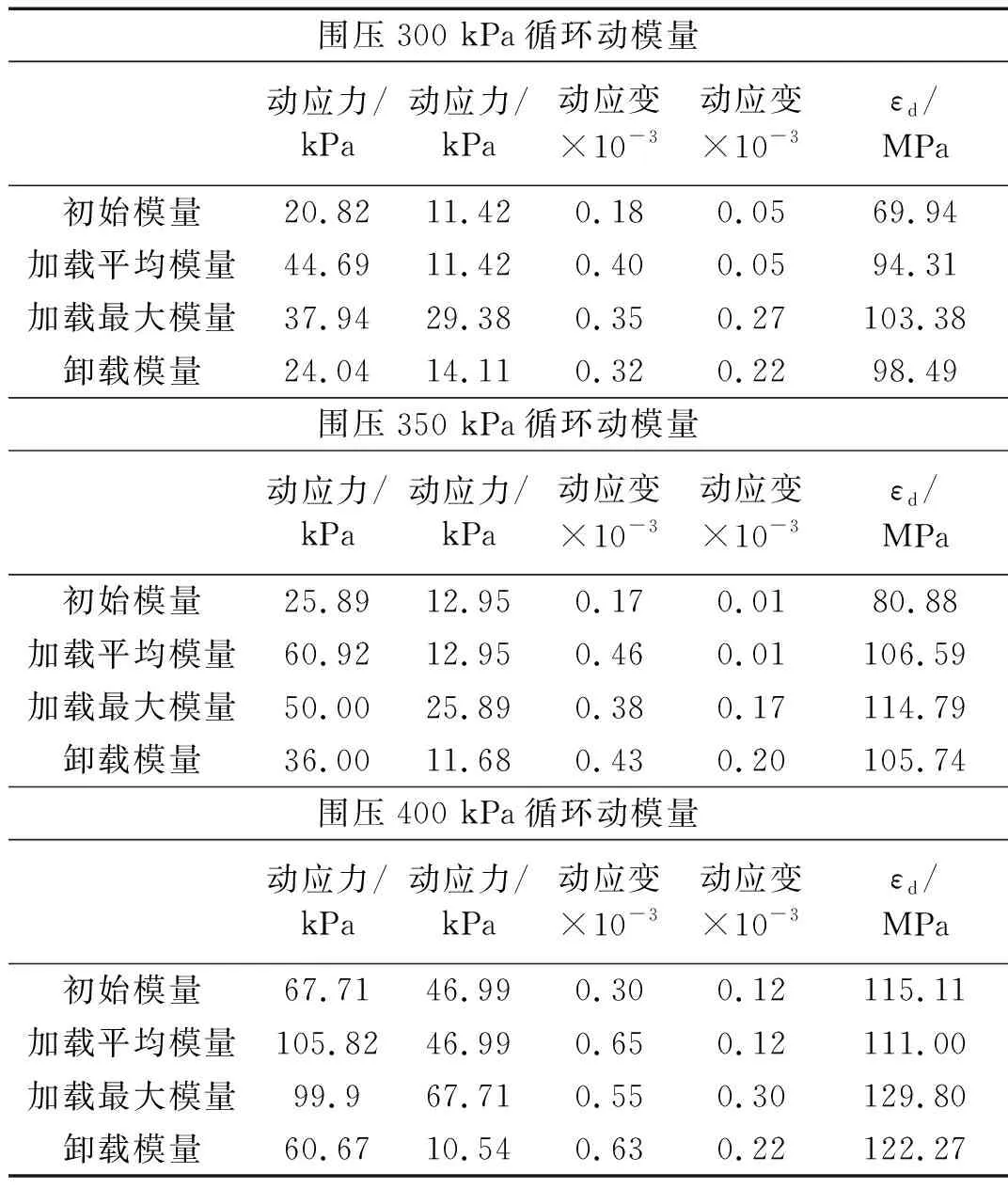
表9 第三組粉質黏土動模量

Bowles對基樁受沖擊時的動力性能進行了分析，采用有限差分式代替描述沖擊波沿樁身傳播的微分方程，樁與樁頂附屬設備相應的有限差分力學模型和具體計算方法參見相關文獻。

3.1.2 樁側土力學模型

(1) 樁側土靜阻力模型

樁側土靜阻力模型如式(2)所示。

(2)

(3a)

式中：Km為單元m樁側土彈簧系數，kN/m；Rum為單元m樁側阻力極限值，kN；Q為土的最大彈性變形，mm；Dm為單元m樁側土的變形，mm。

式(3a)假定各樁側土的最大彈性變形值相同，與實際情況不相符合，本文樁側土最大彈性變形值根據不同土層而分別取值，式(3a)修改為

(3b)

式中，Qm為單元m樁側土的最大彈性變形，mm。

(2) 樁側土動阻力模型

樁側土動阻力模型如式(4)所示

Rdm=RsJsvm

(4a)

式中：Rs為樁側土靜阻力，kN；Js為樁側土阻尼系數，s/m；vm為單元m的速度，m/s。

式(4a)假定各單元樁側阻力和阻尼系數取值相同，與實際情況不相符合，本文樁側阻尼系數和樁側阻力根據不同土層而分別取值，式(4a)修改為

Rdm=RsmJsmvm

(4b)

式中：Rsm為單元m樁側土靜阻力，kN；Jsm為單元m樁側土阻尼系數，s/m。

3.1.3 樁尖土力學模型

(1) 樁尖土靜阻力模型

樁尖土靜阻力模型如式(5)所示

(5)

(6a)

式中：Kp為樁尖土彈簧系數，kN/mm；Rup為樁尖阻力極限值，kN；Q為土的最大彈性變形，mm；Dp為樁尖土的變形，mm。

式(6a)假定樁端土和樁側土的最大彈性變形值相同，與實際情況不相符合，本文樁端土與樁側土采用不同的最大彈性變形值，式(6a)修改為

(6b)

式中，Qp為樁端土的最大彈性變形，mm。

(2) 樁尖土動阻力模型

樁尖土動阻力模型如式(7)所示

Rdp=RspJpvp

(7)

式中：Rsp為樁尖土靜阻力，kN；Jp為樁尖土阻尼系數，s/m；vp為樁尖的速度，m/s。

3.1.4 土的特性

Bowles[1]指出最大彈性變形和阻尼系數只要選取恰當的值，在一般情況下，所算得的結果是合理的。

Holeyma[15]通過高應變測試，對樁端位移與樁端阻力關系進行了研究，研究結果表明樁端阻力在樁端位移大于等于2.5%樁徑的情況下可以充分激發；Zhang等[16]對靜荷載試驗樁端阻力充分激發進行了研究，結果表明樁端阻力在樁端極限位移值為0.5～8.3 mm之間可充分激發。

陳榮保等[17-18]根據前期研究成果，提出部分土層動力參數取值的經驗值：建議部分土層的樁側最大彈性變形和樁側阻尼系數所對應的經驗值可根據表10取值；建議強風化泥質粉砂巖最大彈性變形Qp取值范圍為5.0～12.0 mm，強風化泥質粉砂巖樁尖阻尼系數取值范圍為0.05～0.25 s/m。

3.1.5 程序計算

根據建立的力學模型，采用FORTRAN軟件編制計算程序，通過程序計算可繪出Ru對1/s(每厘米的錘擊數)的曲線圖。在實際工程中，可測得每一錘的貫入度s和計算出錘擊數1/s，根據程序計算的Ru～1/s曲線圖，可得到錘擊管樁的貫入度為s時相對應的極限阻力。

表10 最大彈性變形和阻尼系數

3.2 計算結果

采用改進的方法對試驗樁進行計算。根據動三軸室內試驗結果：隨著樁埋深增加，同種土的阻尼比會隨著下降。因此，隨著土層埋深增加，同種土的阻尼系數取低值。

試驗樁的計算參數為：樁劃分單元數為10；樁側阻力為非線性分布；樁側土最大彈性變形Qm取值見表11；樁端土最大彈性變形Qp為8 mm；樁側阻尼系數取值見表12；樁錘效率系數Ef為0.95；樁尖阻尼系數Jp為0.170。

各試驗樁計算結果的曲線圖見圖5(本文僅列出5根埋有滑動測微計的曲線圖)。根據曲線圖，得出各試驗樁的豎向極限阻力見表13。

表11 各土層最大彈性變形

表12 樁側阻尼系數

(a) 7號樁(b) 8號樁(c) 9號樁

(d) 10號樁(e) 11號樁圖5 極限阻力-錘擊數/厘米的曲線圖Fig.5 Curve of limit resistance to the number of hammers per centimeter

表13 改進數值方法計算結果

4 試驗樁現場試驗測試結果

靜載試驗加卸載方式采用慢速維持荷載法，5根滑動測微計的樁身累計變形曲線圖和樁頂Q-s曲線圖分別見圖6。

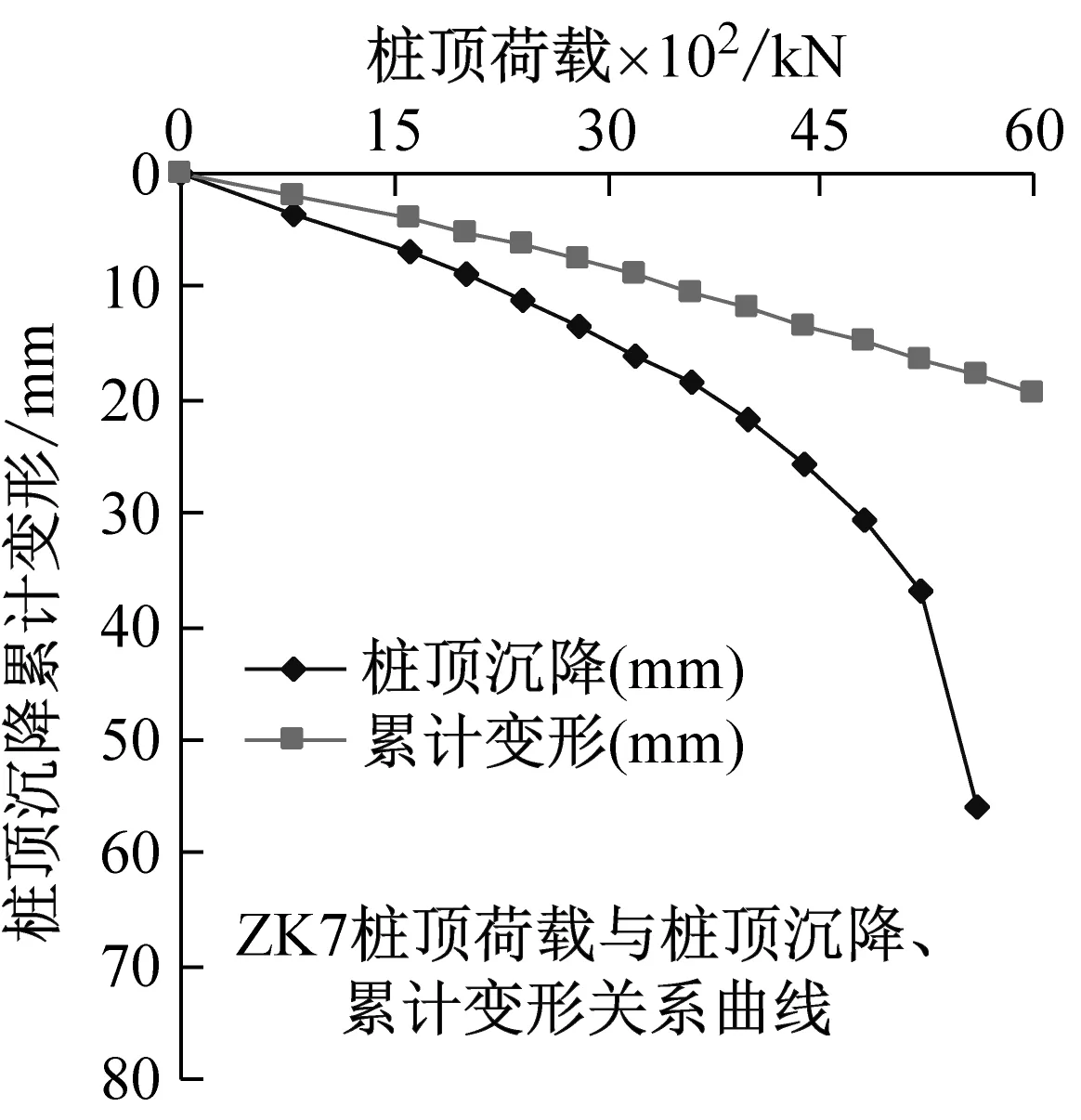
(a) 7號樁(b) 8號樁(c) 9號樁

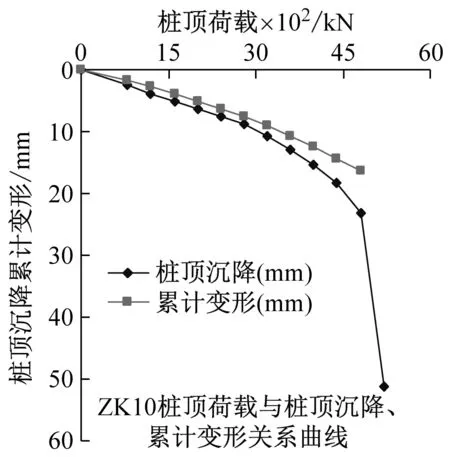
(d) 10號樁(e) 11號樁圖6 各級荷載下樁頂沉降和累計變形關系曲線圖Fig.6 Curve diagram of pile top settlement and cumulative deformation under various loads

4根埋有滑動測微計的φ500試驗樁高應變測試結果圖見圖7。

試驗樁的樁端土最大彈性變形值為6.0～14.3 mm，測試結果具體情況見表14。測試結果表明采用該方法可以解決高強度混凝土預應力管樁內力測試技術難題。確定的樁端彈限位移取值范圍為判斷樁端持力層是否達到極限承載力提供依據。

12根試驗樁靜載試驗的承載力、高應變動測承載力結果見表15。

表14 樁端土最大彈性變形

表15 試驗結果

根據高應變測試曲線擬合法提取各動力參數，樁側阻尼系數為0.41～0.75 s/m，樁錘效率系數為0.91～1.00，12根試驗樁中共有10根試驗樁樁尖阻尼系數在0.08～0.20 s/m范圍內，各系數具體情況見表16。

采用靜載試驗(滑動測微計測試)和高應變測試的5根試驗樁樁端阻力比見表17。從表中可知，高應變測試結果樁端阻力比明顯偏高。

表16 動力參數

表17 樁端阻力比

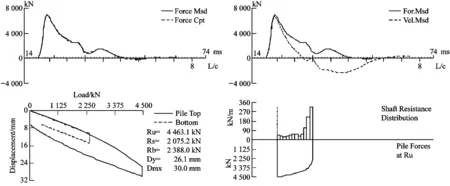
(a) 7號樁(b) 8號樁

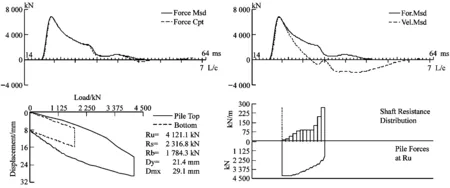
(c) 10號樁(d) 11號樁圖7 高應變曲線擬合法測試結果圖Fig.7 Diagram of curve fitting method of high strain test

5 數值計算與現場試驗對比分析

通過對試驗樁的數值計算和現場試驗，可見：

(1) 采用改進數值方法計算結果與試驗結果基本吻合，具體情況見表18。12根試驗樁的豎向承載力偏差在±15.5%范圍內，表明采用該計算方法預測預應力管樁承載力具有一定的合理性。

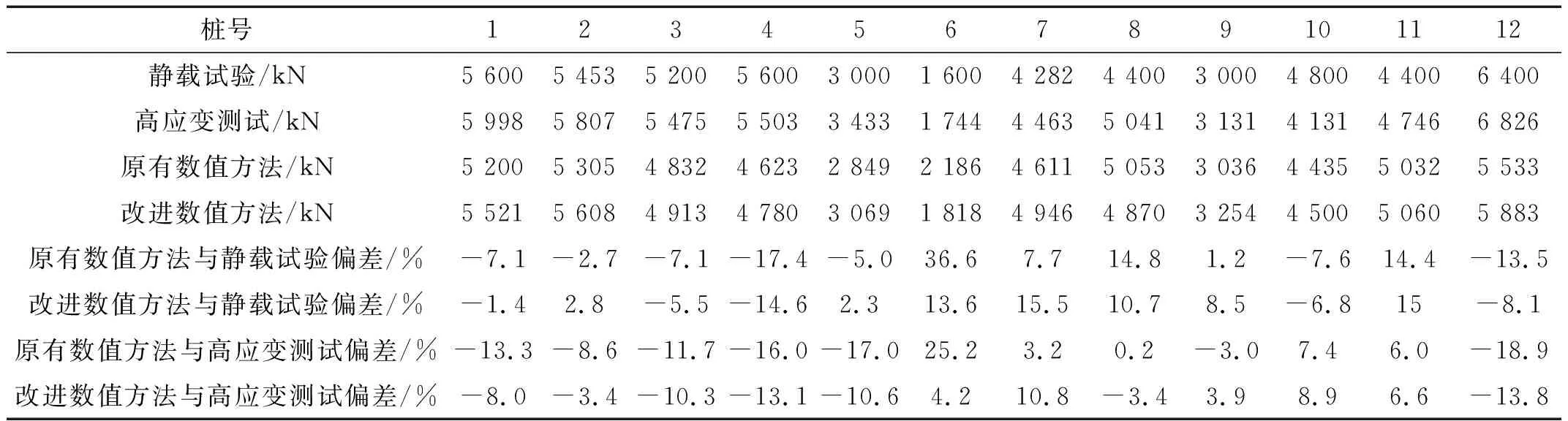
表18 數值計算結果和試驗結果

(2) 改進方法計算結果與靜載試驗結果偏差絕對值在1.4%～15.5%范圍內，原有方法計算結果與靜載試驗結果偏差絕對值在1.2%～36.6%范圍內；改進方法計算結果與高應變測試結果偏差絕對值在3.4%～13.8%范圍內，原有方法計算結果與高應變測試結果偏差絕對值在0.2%～25.2%范圍內。表明改進方法比原有方法計算結果更接近于試驗結果。

(3) 12根試驗樁樁側各土層阻尼系數取值范圍為0.30～0.80 s/m，而高應變結果各試驗樁樁側阻尼系數均值為0.41～0.75 s/m，表明計算方法取值與高應變測試結果相一致。

(4) 12根試驗樁中，數值計算方法樁尖阻尼系數取值為0.17 s/m，而高應變測試結果共有10根試驗樁樁尖阻尼系數在0.08～0.20 s/m范圍內，表明計算方法取值與高應變測試結果相一致。

(5) 12根試驗樁，數值計算方法樁錘效率系數取值為0.95，而高應變測試結果共有10根試驗樁樁錘效率系數在0.91～1.00范圍內，表明計算方法取值與測試結果相一致。故建議強風化泥質粉砂巖持力層樁錘效率系數取值范圍為0.90～1.00。

6 結 論

本文對樁周土進行動三軸室內試驗；采用改進的基樁動測承載力數值計算模型對12根試驗樁進行計算分析；對12根試驗樁進行極限荷載試驗，可得如下結論：

(1) 樁埋深較淺處，土阻尼對于錘擊能量傳遞的消耗較大，故土層分布尤其是較淺部土層分布對高應變錘擊樁時土動力學響應影響較大。

(2) 隨著樁埋深增加，同種土的阻尼比會隨著下降；即隨著樁埋深增加，同種土的樁側阻尼系數會隨著下降，故土層較深時樁側阻尼系數在取值范圍內宜取小值。在實際管樁動測承載力計算時，樁側土埋深小于15 m時，樁側阻尼系數在取值范圍內可取中間值～高值；樁側土埋深大于15 m時，樁側阻尼系數在取值范圍內可取低值～中間值。

(3) 各樁側土層根據土層性質采用不同阻尼系數和最大彈性變形值，解決了傳統上基樁動測承載力計算模型各土層動力參數無法分層分別取值的難題，使基樁動測承載力計算結果更符合實際。

(4) 采用程序計算結果與豎向抗壓靜載試驗結果基本吻合，12根試驗樁的豎向承載力偏差在±15.5%范圍內，說明該程序在分析管樁動測承載力時具有一定的合理性。