基于注意力BiGRU的機械故障診斷方法研究

張立鵬，畢鳳榮,，程建剛，沈鵬飛

(1.天津內燃機研究所，天津 300072； 2.天津大學 內燃機燃燒學國家重點實驗室，天津 300072)

國民生產環節中，機械生產設備連續化、高速化、自動化的趨勢迅猛發展，因此監測設備運行狀態、保障重大產品設備安全穩定運行、防止設備故障帶來的經濟故障和人員傷亡變得愈加重要。狀態監測與故障診斷技術作為一門迅速發展的工程領域技術得到科研人員的廣泛關注。

基于振動信號的故障診斷方法，由于其測量簡單、成本低、采集精度高、適應性強等優良特性，在工程實踐中被廣泛應用[1]。基于振動信號的機械狀態檢測與故障診斷一般包括特征提取和模式識別兩個階段。當機械系統如軸承等關鍵部件發生故障時，瞬時沖擊響應成分將通過結構傳播到傳感器，儲存于采集到的信號數據中，這種成分表現出持續時間較短、頻帶較寬等特點，通過分析處理這種帶有時變特性的非平穩信號，便可以得到機械的故障類型。目前，處理和分析非平穩信號時，短時傅里葉變換(short time transform,STFT)、小波變換(wavelet transform,WT)、稀疏表達[2](sparse representation,SR)、經驗模態分解[3](empirical mode decomposition,EMD)、變分模態分解[4](variational mode decomposition,VMD)等方法都取得了不錯的效果，對于特定的故障類型實現了較好的分類準確性，但都存在自適應性差、算法復雜、過于依靠先驗知識、過于依賴所提取特征的質量等局限性。

隨著深度學習的興起，基于神經網絡的人工智能模型被引入機械故障診斷領域。神經網絡模型經過不斷優化發展，實現了較高的分類準確度，并具有較強的魯棒性和容錯能力，能夠充分逼近機械故障類型識別中十分復雜的非線性關系。近年來，循環神經網絡(recurrent neural networks,RNN)在時間序列數據特征挖掘領域有著很高的地位，門控循環單元[5](gated recurrent unit,GRU)和長短期記憶網絡[6](long short term memory networks,LSTM)等RNN變體在關于時間序列的預測問題領域獲得了巨大的成功。本文將以機械故障(以軸承故障和柴油機典型故障為例)振動信號這一典型時間序列預測問題為研究對象，以GRU為主要研究方法，搭建雙向門控循環單元(bidirectional gated recurrent unit,BiGRU)網絡模型實現“端到端”的機械故障診斷。同時，引入注意力機制，進一步提升模型對于長序列數據的學習能力，實現更優的故障診斷效果。

1 算法原理

1.1 循環神經網絡

循環神經網絡是用于分析時間序列數據的網絡模型，其改變了傳統人工神經網絡的前饋機制。在前饋型神經網絡中，信息經輸入層輸入，正向輸出信息到下一級直至輸出層輸出結果，整個網絡結構中無信息反饋，因此前饋型神經網絡沒有時間特性，輸入之間不相關聯，在處理時間序列問題時效果不佳。而對于機械故障振動信號而言，輸入信號的特征是有時間關聯性的。RNN在前饋型神經網絡的基礎上引入了時間序列的影響，將隱藏節點定向連接成環，這樣有利于網絡對時間信息的傳遞，展示動態時序行為，進而挖掘時間序列的特征[7]，其示意圖如圖1所示[8]。

圖1 RNN結構示意圖Fig.1 Schematic of the RNN architecture

RNN的前項傳播公式如式(1)～(4)所示。

(1)

(2)

(3)

(4)

式中:x為網絡輸入;y為網絡輸出;w為權重;z為神經元的加權和;f為神經網絡激活函數;s為神經元激活值;t為網絡當前時刻;I為輸入向量維度;i為輸入向量下標;H為隱藏層單元向量維度;h為t時刻隱藏層單元向量下標;h′為t-1時刻隱藏層單元向量下標;o為輸出向量下標。

根據結構圖和前向傳播公式，RNN隱藏層st不僅取決于當前時刻的輸入xt，也取決于上一時刻隱藏層輸出st-1。表現出RNN不僅能接收到當前時刻樣本的信息，也能接收上一時刻的信息，即RNN具有了時間特性。將式(1)～(3)迭代入式(4)，可以得到式(5)，表示最終時刻的輸出結果包含了整個時間序列的特征信息。

(5)

1.2 雙向門控循環單元

門控循環單元神經網絡是RNN的一種變體，其利用特殊的“門”結構作為記憶單元替代了傳統RNN的神經元結構，解決了RNN在處理長時間序列時因梯度消失而易陷入局部最優的問題。

rt=σ(Wrhht-1+Wrxxt)

(6)

zt=σ(Wzhht-1+Wzxxt)

(7)

(8)

(9)

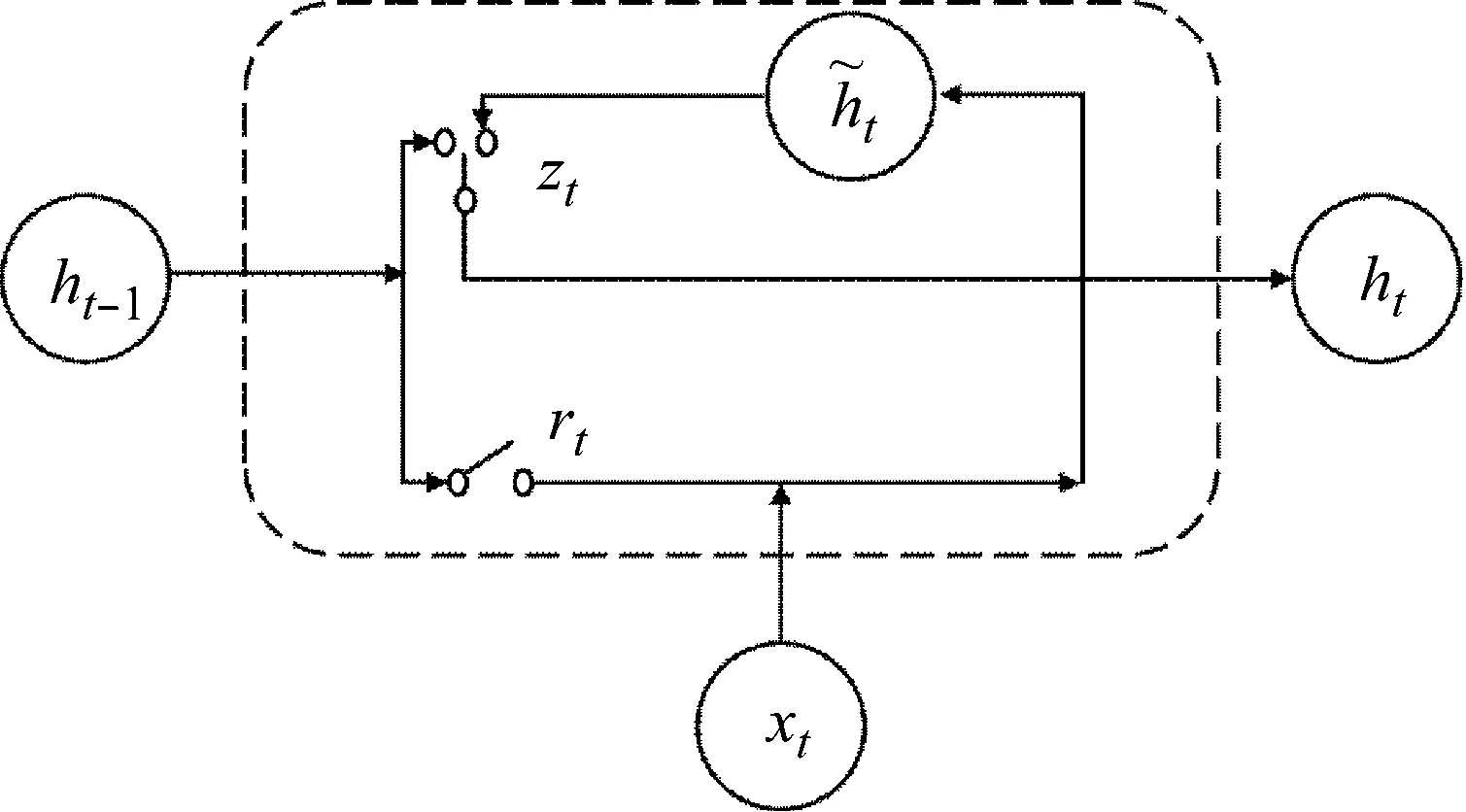
圖2 GRU內部結構Fig.2 Inner structure of GRU

(10)

1.3 注意力機制

注意力機制在自然語言處理[11]、圖像分類[12]、文本分類[13]等任務中都取得了成功。本文將注意力機制引入故障診斷領域。具體地，對于BiGRU網絡的各時間節點輸出H=[h1,h2,h3…,hL](L表示序列長度)，通過分配一個權重系數S=[s1,s2,s3,…,sL]。可以有選擇性地關注整個序列數據中的不同位置信息。詳細原理如式(11)所示

H′=tanh(H)

S=softmax(αTH′)

y=HST

(11)

式中：α為可學習參數，采用隨機初始化方式給點初始值，通過反向梯度下降算法計算；y為最終輸出結果。可以發現，最終輸出y不再單純依賴最后時間節點輸出，而是綜合各個時間節點輸出的結果。注意力機制的引入，可以有效地解決BiGRU對于過長序列數據學習效率低的問題。

2 基于注意力BiGRU的故障診斷模型

圖3 基于注意力BiGRU的故障診斷模型Fig.3 Fault diagnosis model based on attention BiGRU

3 實例分析

3.1 數據集介紹

本文將在公開數據集——美國凱斯西儲大學軸承數據集，以及柴油機實驗故障數據集上驗證模型的有效性。

其中美國凱斯西儲大學數據實驗包含內圈故障、滾動球故障以及外圈故障(3點鐘、6點鐘、12點鐘位置)，故障損傷直徑分別為0.007、0.014、0.021和0.028英寸(1英寸=2.54 cm)。本文將選用正常、內圈故障、滾動球故障以及外圈故障(6點鐘方向)4種狀態數據，每類故障狀態包含損傷直徑為0.007、0.014、0.021英寸的3種故障程度，因此共包含10類故障狀態。

采樣頻率為48 kHz，電機工作轉速為1 750 r/min。軸承每轉一圈采樣點數為1 646，為保證每個樣本均包含一個完整的周期，本文將樣本長度定為1 680。為增加神經網絡訓練數據量，本文將用重疊采樣的方式對原始數據進行截取。對于訓練數據，重疊率為50%，對于測試數據，將采用無重疊方式截取。最后共得到10類樣本數據，每類數據包含376個訓練樣本和100個測試樣本。在軸承數據集中，樣本長度為Lb=1 680，取db=7，則Tb=240。

柴油機故障數據實驗在一臺某型直列六缸柴油機上進行，該柴油機的性能參數如表1所示。

表1 某型柴油機主要參數

主要采集柴油機的缸蓋振動加速度信號，傳感器布置在1～3缸的缸蓋上，實驗柴油機臺架示意以及傳感器的布置位置如圖4所示。

圖4 實驗用柴油機以及傳感器布置Fig.4 The experimental diesel engine and thelocation of the sensors

實驗主要模擬了氣門間隙異常故障、噴油軌壓異常故障、噴油提前角故障以及供油量不足四種故障類型，并且對其中每一類故障發生的不同程度進行了模擬。總共包括13種故障狀態，對應樣本標簽0～12。詳細介紹如表2所示(其中氣門間隙異常故障數據的兩個數字分別代表進氣門間隙與排氣門間隙，單位：mm)，短線后的數字為對應的樣本標簽)。設置柴油機轉速穩定為1 600 r/min，并且保持滿負荷的工作狀態，觀察測試信號，待其穩定后開始測量并記錄數據。

表2 模擬故障工況表

采樣頻率為25.6 kHz，柴油機轉速為1 600 r/min，柴油機每個工作周期采樣點數為1 920。于是本文將樣本長度設為1 920，保證每個樣本內包含一個完整工作周期。同樣地，按照軸承數據截取方法進行處理數據。最后獲得每類狀態數據164個訓練樣本和50個測試樣本。

在柴油機實驗數據集中，樣本長度為Le=1 920，取de=8，則Te=240。

3.2 實驗驗證

本文將時域信號直接輸入模型，以交叉損失熵為目標函數，通過反向梯度下降算法訓練每一層網絡參數，每批次訓練輸入樣本數B_S=256，采用指數衰減學習率，學習率LR表達式如式(12)所示。模型各個網絡層詳細參數如表3所示。

LR=lr*decay_rate(epoch/decay_steps)

(12)

其中：lr=0.01,decay_rate=0.9，epoch為訓練次數，decay_steps=40。

表3 注意BiGRU模型參數

將本文模型與單一的BiGRU進行對比，單一的BiGRU模型層數為3，每層隱藏神經元個數依舊為32，在BiGRU輸出層緊接一個Dropout層，Dropout比例為0.5。兩模型在上述兩種數據集上訓練對比如圖5所示。

如圖5(a)所示，在軸承數據集上，經過大約60次迭代訓練之后，本文模型便完全收斂，達到了99.95%的訓練準確率。但是BiGRU模型經過大約200次訓練以后，模型才大致收斂，訓練準確率在98%左右，可以看出，在軸承數據集上，和原始BiGRU模型相比，本文模型可以有效縮短三分之二的訓練時間，并且取得更好的訓練效果，訓練也更加穩定。

(a) 軸承數據集

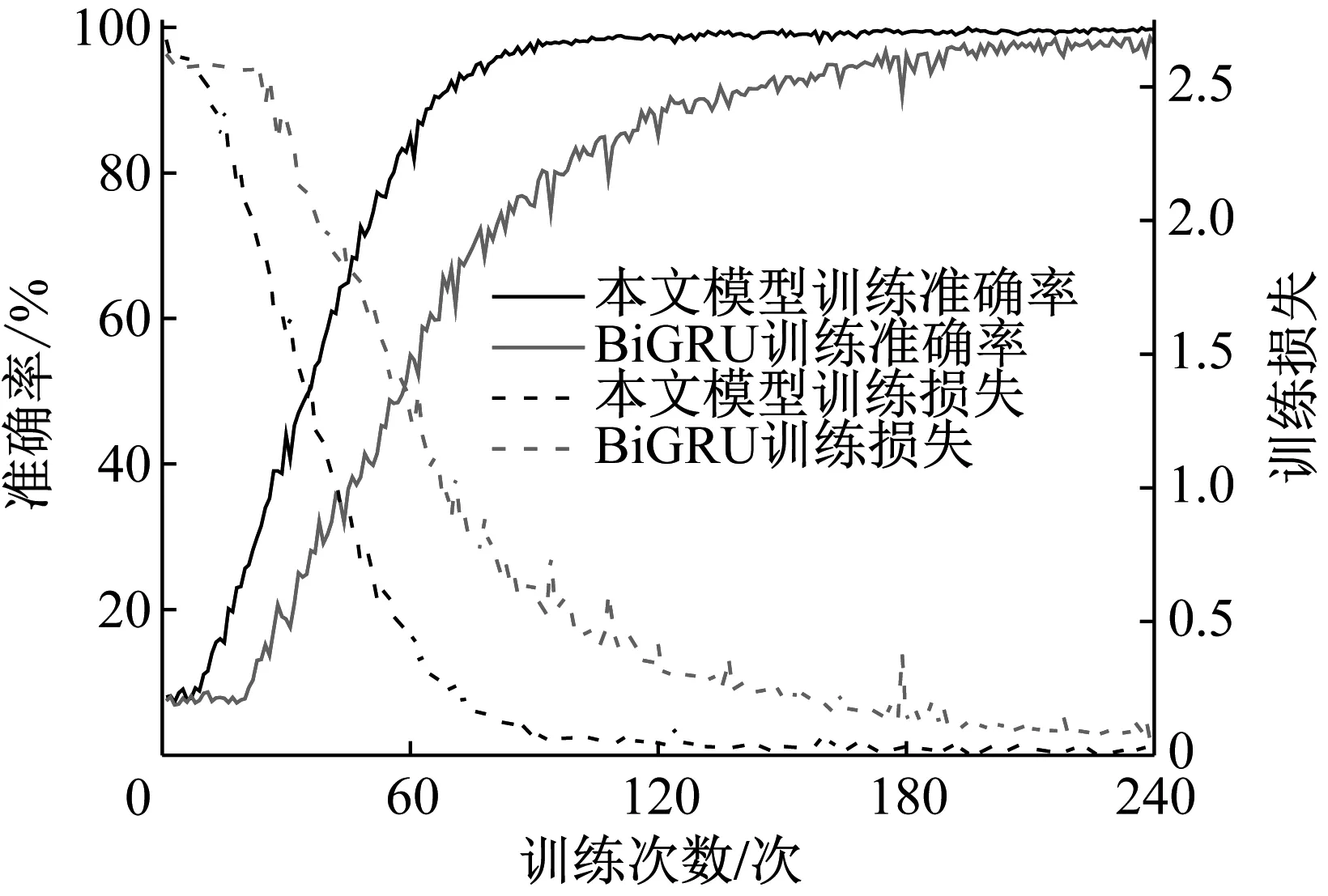
(b) 柴油機數據集圖5 本文模型與BiGRU訓練對比圖Fig.5 Training comparison between the attention BiGRU andtraditional BiGRU

如圖5(b)所示，在柴油機故障數據集上，本文模型經過了大概90次訓練之后便收斂，達到99.82%的訓練準確率。但是，BiGRU模型經過大約180次訓練以后才大致收斂，訓練準確率在98%左右小幅波動，與本文模型訓練結果相比，訓練損失比本文模型波動也更大，進一步證明本文模型在在有效縮短訓練時間的同時能夠獲得到更佳的訓練效果。

測試準確率常用來驗證模型的有效性。筆者將分別在軸承數據集和柴油機數據集上測試本文模型和BiGRU模型的測試準確率，測試次數為10次，取平均值作為最終測試結果，具體結果如表4所示。

表4 本文模型與BiGRU測試準確率對比

本文模型在軸承數據集上測試精度比BiGRU高了1.20%，在柴油機數據集上測試精度比BiGRU高了1.69%。不同數據集上的對比結果均表明本文模型具有更高的診斷精度。同時，可以看出，10分類軸承數據集診斷任務難度較低，而13類柴油機故障診斷任務難度較大，但本文模型依舊能夠取得91.38%的好成績。

為了進一步驗證本文模型對于原始數據特征的提取能力，本文采用t分布隨機鄰域嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法對柴油機實驗數據集進行降維可視化分析。具體地，分別將柴油機原始時域數據以及本文模型輸出數據映射到2維空間，分別命名為t-SNE1和t-SNE2。可視化結果如圖6、圖7所示。

圖6 原始數據特征分布可視化Fig.6 Visualization of raw data features via t-SNE

圖7 輸出數據特征分布可視化Fig.7 Visualization of output data feature via t-SNE

從圖6、圖7中可以看出，本文模型可以有效地從原始數據中提取出可分性極佳的數據特征。圖6中的各類數據特征相互重疊，無法直接進行區分。經過本文模型的自適應學習處理之后，可以得到聚類特征非常明顯的結果。也進一步證明了本文模型可以從原始數據特征中提取出具有明顯差異的數據特征。

3.3 魯棒性分析

抗噪能力是評估模型性能的一個重要指標。為進一步測試本文模型在噪聲干擾下的精度變化情況，將采用3.1節所述軸承數據訓練集對本文模型進行訓練。然后在3.1節所述軸承數據測試集中添加不同信噪比的高斯白噪聲，用于測試模型精度，信噪比范圍為-4～10 dB。信噪比定義如式(13)所示，本文模型和BiGRU對比結果如圖8所示。

(13)

圖8 各模型在不同噪聲環境下測試準確率Fig.8 Test accuracy of each model under differentnoise environment

如圖8可以看出，本文模型在不同噪聲環境下表現均優于BiGRU。測試信號混入的噪聲越嚴重，本文模型的精度優勢越明顯，對于信噪比為-4 dB測試信號，本文模型測試精度比BiGRU高6%。

實驗結果表明本文模型對于噪聲干擾具有魯棒性，該效果得益于注意力機制的引入。原始BiGRU模型中，最終結果完全依賴最后時間節點隱藏狀態輸出，其對于越早輸入網絡的信息遺忘越嚴重。因此，在噪聲的干擾下，本就有部分信息缺失的問題導致其分類準確率受到更大影響。但是本文模型通過對各時間節點分配自學習得到的注意力權值以后，使得最終的輸出結果可以有效地考慮整個序列信息，能夠保留完整序列信息的能力使得其受到噪聲的干擾較小，具有更強的魯棒性。

4 結 論

本文進行了利用振動信號進行機械故障診斷的研究，提出了一種基于循環神經網絡的故障診斷方法。該方法首先將采集到的振動信號進行折疊預處理，再利用數據集進行訓練，搭建基于雙向門控循環單元的神經網絡模型，實現了“端到端”的特征提取和故障模式分類過程，同時利用注意力機制進行模型優化，提升了計算效率和診斷準確性。

本文利用美國凱斯西儲大學公開軸承數據集和自采集的柴油機故障振動信號進行了方法驗證，故障診斷結果表明本方法實現了有效的故障類型診斷，且分類準確性和計算效率相較于模型優化前實現了一定程度的提升，并表現出了更有的抗噪能力。

結果表明，循環神經網絡對于解決機械故障診斷類型的時間序列預測問題具有一定的優越性，且對于復雜的柴油機系統仍能表現出良好的性能，循環神經網絡及其優化方法在機械故障診斷領域具有巨大的潛力可供挖掘。