基于集成學習的列車輪徑預測方法
樊澤園、宋曉娟、林立、李雪
(1.山東交通學院,山東 濟南250307;2.軌道交通安全技術與裝備實驗室,山東 濟南250307)
0 引言
當前中國列控車載系統普遍運用速度傳感器進行測速定位,其計算精度直接受到輪徑值變化的影響,若不及時更新系統存儲的輪徑值則會增大測速定位誤差,影響行車安全。
鐵路行業內關于列車輪徑校準的研究,有基于多傳感器融合實現輪徑校準[1,2]。文獻[3]則提出基于灰色算法進行輪徑值的預測。BP神經網絡是目前應用最廣泛的基本神經網絡,有較強的非線性映射能力及預測精度,可根據歷史數據自動提取有用知識。而神經網絡集成的提出則能解決BP存在收斂速度較慢、泛化能力較差、極易獲得局部極小點問題。
1 速度傳感器工作原理分析
速度傳感器通過脈沖計數獲得測量周期內的車輪轉數并乘以輪周長來計算列車行駛速度,其具體公式如下:
式(1)中:n為本次測量周期的脈沖計數值;T為本次測速周期;d為車輪直徑;N為車輪旋轉一圈傳感器發出的脈沖測量值。
在式(1)中,輪徑值d是影響其計算精度的關鍵參量。d隨著列車行駛距離的增加變小,所以必須及時更新系統存儲的車輪輪徑值,降低測速測距誤差。
本文針對鐵路局存儲的列車走行公里報表,引入智能算法提取有用數據進行分析建模,尋找列車輪徑值y和列車行駛距離x之間的對應關系,即
在學習階段,通過訓練生成映射關系f,在預測階段根據新輸入的列車行駛里程來求得當前的列車輪徑值,實現智能預測。
2 Bagging集成BP網絡的預測方法
集成學習用于提高機器學習泛化能力,Bagging算法是其典型算法,并衍生成多個BP子網絡,其核心思想是:給定1個訓練集和1個學習算法,對訓練集進行T次重采樣,每次采樣從訓練集中取m(m<n)個樣本進行訓練,訓練結束后將取樣放回到訓練集,經過訓練后得到多個訓練預測函數f1,f2…fT。最終的集成學習器預測函數f是經過加權平均合成的,并對新的輸入數據進行預測。算法的具體步驟如下。
第一步,數據預處理:原始樣本數據集O={(x1,y1),(x2,y2)…(xn,yn)},采用極差標準化法對樣本歸一化處理,如公式(3),使輸入數據值在[0,1]范圍內。
式(3)中:xi0為歸一化后的第i個輸入值;xi為第i個原始輸入值;xmax為原始輸入最大值;xmin為原始輸入最小值。然后對數據集重采樣T次,生成不同的訓練子集。
1.2.1 標本采集 該孕婦接受檢測前的遺傳咨詢并簽署同意書,根據孕周行羊膜腔穿刺,在B 超探頭引導下行羊膜腔穿刺術抽取羊水30ml進行培養以及染色體微陣列分析(chromosomal microarray analysis, CMA)。
第二步,根據不同的訓練子集,并行訓練不同的BP子網絡,經過訓練學習后能夠得到不同的預測函數ft。
第三步,最終將各個子學習模型的預測函數進行加權平均獲得集成學習器的預測函數
式(4)中:ωt為第t個預測函數在集成中所占的權重。權重值ωt大小則根據子網絡的泛化能力決定,利用未抽到的樣本集計算子網絡的相關系數R,R越大,ωt就越 大,且=1。
第四步,通過學習得到映射關系f(x),就可以輸入新的列車行駛里程xnew,從而預測當前位置對應的列車輪徑值ynew。
3 BP子網絡的設計
針對本文研究對象,設計BP子網絡為一個單輸入單輸出的三層神經網絡,其輸入層是列車行駛里程x,網絡輸出為列車輪徑值y,隱含層選取Sigmoid函數,輸出層為線性激活函數,w=(w1,w2…wj)是輸入層到隱含層的權值向量,v=(v1,v2…vj)是隱含層到輸出層的權值向量。
那么本文將最優化誤差平方和作為誤差準則,即
式(5)~式(6)中:N為樣本個數,εi為誤差絕對值,y′i為第i個實際輸出,yi為第i個理想輸出。
選用均方根誤差(RMSE)作為評價指標,其公式如下列式(7)所示。
用相關系數R來評價子網絡的泛化能力,并確定集成學習中各個子網絡的權值ωt的大小,則第t個子網絡的相關系數為:
本文分別采用自適應學習率的梯度下降法、BFGS擬牛頓Levenberg-Marquardt算法、彈性梯度下降法進行訓練學習,隱含層神經元的個數由經驗公式進行確定,即
式(8)中:a,b分別為輸入層和輸出層單元個數,α∈(1,10),故子網絡隱含層的神經元個數可取范圍為[2,10]。
4 實驗仿真
本文以上海鐵路局提供的CRH2型動車組的列車車輪尺寸相關數據為基礎,研究行車里程與輪徑值動態變化的映射關系,其標準直徑為mm,隨著列車的運行輪徑值會單調變小。對于原始數據集D,共有152組相關數據,其部分數據如表1所示。
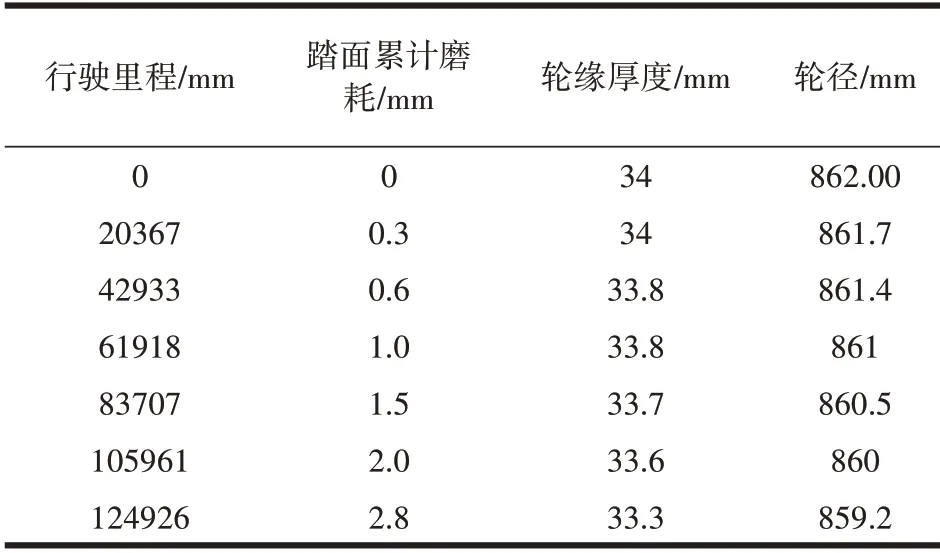
表1 車輪相關數據(部分)
隨機選取112組數據作為原始訓練集O,剩余作為測試集來驗證算法的泛化能力。并在Matlab環境下進行算法編程與仿真驗證,對訓練集O進行6次重采樣生成不同的子訓練集Ot,從而訓練生成6個不同的BP子網絡。利用函數newff來創建BP子網絡,隱層采用tansig函數,輸出層采用purelin函數,隨機產生網絡的權值、閾值,目標誤差設為10-5,最大迭代次數設為500。對于隱層神經元個數,通過比較不同神經元個數下的子網絡收斂誤差來確定最佳神經元個數,以BP子網絡1為例進行說明,其訓練函數設為trainlm,其最佳神經元個數是8。對不同的BP子網絡,采用不同訓練算法。最后用本文的Bagging集成BP網絡算法進行網絡集成,并將其預測效果同單個BP網絡的預測效果、灰色預測法進行對比分析。
在圖1中將灰色預測法、Bagging集成BP子網絡的強預測器的測試集預測誤差絕對值同6個BP子網絡的預測誤差絕對值的平均值進行比較,從中看出本文算法的預測誤差絕對值明顯比另外兩種算法要小,且誤差波動范圍小,說明本文算法的預測精度較高,驗證了本文算法的有效性,其預測結果接近列車輪徑的真實值。
根據鐵路局車務段存儲的列車輪徑值相關記錄數據,提出運用Bagging算法集成BP網絡的智能算法實現列車輪徑值的預測更新。實驗證明運用Bagging算法集成學習可以提高集成學習器的泛化能力,避免神經網絡普遍存在的過擬合現象,并獲得比灰色預測、單一BP神經網絡更好的預測效果;能夠較好地根據行車里程對列車輪徑值的進行預測,從而在列車行駛過程中進行預測,自動更新車載系統的輪徑存儲值,提高速度傳感器的計算精度,減少人為工作量,并保證行車安全。

