“一核四維”，強化運算能力、促進深度學習

陶蕊 談玉琴

[摘? 要] 隨著知識創新時代的到來，深度學習正成為基礎教育改革的新趨勢. 深度學習要求學習者掌握非結構化的深層知識，并進行批判性高階思維的打造、主動的知識構建、有效的遷移應用及真實問題的解決，進而實現問題解決能力、批判性思維、創造性思維、元認知能力等高階思維和能力的發展. 數學運算是新課標六大數學核心素養之一，是促進深度學習的有效載體. 文章以強化圓錐曲線的運算能力、促進深度學習為核心，從四個維度（運算根基、運算方向、運算速度、運算經驗）淺談圓錐曲線教學中強化運算能力、促進深度學習的實踐與探索.

[關鍵詞] 運算能力;深度學習;圓錐曲線

富蘭在《極富空間》一書中提出：“深度學習的目標是：使學生獲得成為一個具有創造力的、與人關聯的、參與合作的終身問題解決者的能力和傾向.”深度學習既是一個學習個體主動建構知識的過程，又需要學習主體之間將知識和信息進行交換和重組. 深度學習是在具體的學習過程中實現的. 數學運算不僅是解決數學問題的必備條件，也是促進深度學習的有效載體.

[?]概念的界定

（1）數學運算是指在明晰運算對象的基礎上，分析運算條件、依據運算法則解決數學問題的過程. 主要包括理解運算對象、掌握運算法則、探究運算方向、選擇運算方法、設計運算程序、求得運算結果等.

（2）深度學習. 布魯納說過：“學習存在表層和深層兩個過程，掌握知識經驗的過程是學習的表層，而通過掌握知識，形成一定的思考方式、學習態度，增強解決問題的能力和自信才是學習的深層過程，真正的學習包括獲取知識、發展能力和形成態度.”所以，深度學習是相對于淺層學習而言的，是一種基于理解的學習，因此理解批判性思維、整合學習內容、構建知識體系和有效進行知識遷移的學習活動，是構建高效課堂、內化核心素養的重要途徑.

[?]圓錐曲線教學中強化運算能力的目的與意義

著名的數學家波利亞指出：“掌握數學就意味著善于解題.”運算能力是善于解題的必備條件，是高中生應該具備的一種重要的數學能力. 圓錐曲線是高考數學的命題熱點，從近幾年浙江省高考數學試卷的結構來看，2道填空題和選擇題小題，1道解答題大題，分值大概30分左右. 解題的特點是入口很寬、方法靈活、運算量大，但是很多學生“敗”在了運算上，得分率偏低，所以強化圓錐曲線的運算能力顯得尤為重要！

（1）激發學習興趣，提升運算素養.“成功的教學不是強制，而是激發學習興趣.”運算來源于學習活動本身，為學生提供了一種情境，使其在多元的運算剖析與評價活動中，克服畏難心理、增強學習興趣，強化運算能力、促進深度學習.

（2）優化思維品質，發展創新能力.美國心理學家吉爾福特指出：“人的創新能力必須要有敏銳的洞察力，要能夠透過事物的表面現象把握其內在本質特性.”深度剖析運算算理，厘清運算本質;領悟運算經驗，優化思維品質，發展創新能力.

（3）教學相長，促進教師專業發展.美國教育心理學家波斯納提出了一個教師成長公式：教師成長=經驗+反思. 通過強化運算能力的研究促進教師反思，反思學生的“學”、反思自己的“教”，在反思中改進教學策略，提升教學效益，促進專業發展.

[?]圓錐曲線教學中強化運算能力、促進深度學習的實踐與探索

荷蘭著名的數學教育家弗賴登塔爾曾指出：“數學教育方法的核心是學生的再創造.”圓錐曲線中蘊含著豐富的運算方法與技能，是培養學生運算素養和再創造能力的重要載體. 教師要整合資源、搭建平臺，從夯實運算根基、指明運算方向、提升運算速度、鞏固運算經驗四個維度，幫助學生在運算的過程中用自己的體驗、自己的思維，重新創造有關的數學知識，提升運算能力、促進深度學習.

1. 強化概念，夯實運算根基、促進深度理解

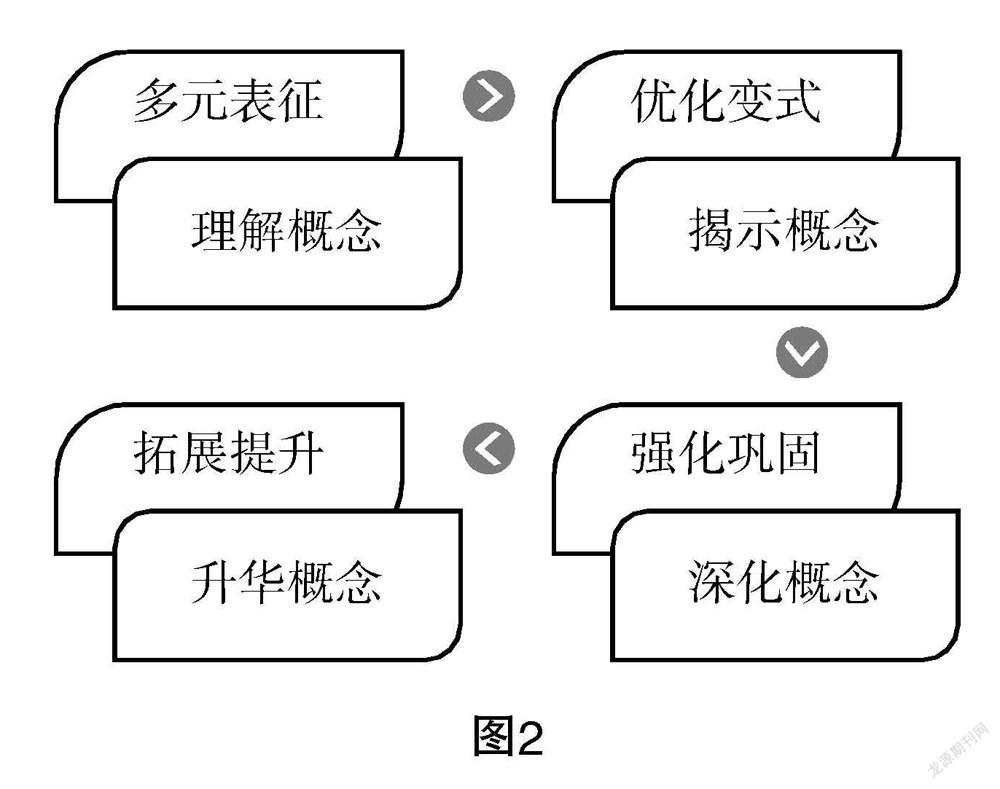
李邦河院士說過：“數學根本上是玩概念的，不是玩技巧，技巧不足道也.”圓錐曲線的概念是其一切幾何性質的“根”與“源”，是解幾何綜合題的重要背景，也是高考數學試題考查的重點. 教學中要挖掘概念的深層次內涵，從更高的層面尋求深化的認識過程，搭建知識框架、感悟數學思想，夯實運算根基、促進深度學習.

（1）多元表征，深度理解概念、內化核心素養. G·波利亞曾經說過：“學習任何東西，最好的途徑是自己去發現，因為這種發現理解最深，也最容易掌握內在的規律和聯系.”創設教學情境，幫助學生探究概念的起源及發展、挖掘概念的多元表征、構建概念的認知結構，多元聯系、多維比較，促進學生深度理解圓錐曲線的概念，為數學運算提供優良的中樞端，內化核心素養.

案例1：多元表征視角下的兩道高考試題.

題1：（2015年浙江省高考數學文科第7題）如圖4所示，斜線段ΑΒ與平面α所成的角為60°，B為斜足，平面α上的動點P滿足∠PAB=30°，則點P的軌跡是（? ）

A. 直線 B. 拋物線

C. 橢圓 D. 雙曲線的一支

題2：（2008年浙江省高考數學理科第10題）如圖5所示，AB是平面α的斜線段，A為斜足. 若點P在平面α內運動，使得△ABP的面積為定值，則動點P的軌跡是（? ）

A. 圓B. 橢圓

C. 一條直線 D. 兩條平行直線

（2）優化變式，揭示概念本質、內化核心素養.許多運算錯誤是由于對概念的理解有偏差：理解不全的概念、模糊近似的概念、張冠李戴的概念等. 這就需要優化概念的變式教學、揭示概念的本質，在對比優化中幫助學生理清概念的內涵與外延，為在運算中準確應用概念掃清障礙.

案例2：橢圓與雙曲線本質的差異.

題3：如圖6所示，圓O的半徑為定長r，P是圓上任意一點，A是圓O內一定點，線段AP的垂直平分線l和半徑OP相交于點Q，當點P在圓上運動時，點Q的軌跡是什么？為什么？

變式：如圖7所示，A是圓O外一定點（注：其他條件與題3相同），點Q的軌跡是什么？為什么？

（3）強化鞏固，深化概念應用，發展核心素養. 設計與概念有關的微專題，強化概念的應用，體會圓錐曲線概念的內涵與外延，體驗在遇到不同問題的情境下巧妙回歸定義、規避復雜的運算，從而達到事半功倍的愉悅心理狀態. 在感悟與體驗中提升運算能力、發展核心素養.

（4）拓展提升，升華概念精髓，發展核心素養.日本數學教育家米山國藏說過：“在學校所學到的數學知識，在進入社會后不到一年兩年就忘掉了. 然而，不管他們從事什么工作，唯有深深銘刻于頭腦中的數學精神和數學思想方法卻長期地在他們生活和工作中發揮著作用.”數學概念是思想方法的發源地，在教學中要提煉蘊含于概念中的思想方法，升華概念精髓. 在拓展訓練中將知識內化，提升運算的思維品質，培育創新能力、發展核心素養.

案例3：巧借類比思想，升華概念精髓.

G·波利亞說過：“類比是一個偉大的引路人.”在數學教學與研究中，類比是進行合情推理的一種非常重要的思維方法. 高中數學新課程已經將“類比推理”能力的培養作為了課程目標之一，在近幾年的高考中也大量出現了能力立意，“多一點想，少一點算”的類比題. 圓與橢圓是兩類重要的有心二次曲線，圓的很多性質及與其相應的解題方法可以與圓錐曲線類比.

題4：（2012年浙江省高考數學理科第21題）如圖9所示，橢圓C：+=1（a>b>0）的離心率為，其左焦點到點P（2，1）的距離為，不過原點O的直線l與C相交于A，B兩點，且線段AB被直線OP平分.（1）求橢圓C的方程;（2）求△ABP面積取最大值時直線l的方程.

題5：（2013年浙江省高考數學理科第21題）如圖10所示，點P（0，-1）是橢圓C：+=1（a>b>0）的一個頂點，C的長軸是圓C：x2+y2=4的直徑.l，l是過點P且互相垂直的兩條直線，其中l交圓C于A，B兩點，l交橢圓C于另一點D. （1）求橢圓C的方程;（2）求△ABD面積取最大值時直線l的方程.

題6：（2014年浙江省高考數學理科第21題第（1）問）如圖11所示，設橢圓C：+=1（a>b>0），動直線l與橢圓C只有一個公共點P，且點P在第一象限. 已知直線l的斜率為k，用a，b，k表示點P的坐標.

2. 優化策略，指明運算方向、促進深度思考

“人的一生，是一連串決定交織而成的過程，其精華在于自己如何選擇. 生命的最高境界，就是選對舞臺，盡情揮灑才華，走出自己的路. ”所以解決問題需要最優的解法，“方法大于苦干”. 浙江省高考數學的命題特點為：能力立意，“多一點想、少一點算”. 所以選擇運算策略顯得尤為重要. 筆者對2014年至2020年共七年全國各地關于圓錐曲線的高考題進行了分析，并結合浙江省高考數學的命題特點及其教學實踐，提煉了圓錐曲線優化運算的6種常用策略（見圖12），在解題中可以穿插運用，幫助學生指明運算方向、優化運算方法，在對比優化中促進深度思考、發展核心素養.

策略.

題7：已知點A（x1，y1），B（x2，y2）是拋物線y2=4x上相異兩點，且滿足x1+x2=2.? （1）若AB的中垂線經過點P（0，2），求直線AB的方程;（2）若AB的中垂線交x軸于點M，求△AMB面積的最大值及此時直線AB的方程.

（1）對比多元運算方法，優化選擇意識：

（2）反思算法，形成策略，提升運算能力：

3. 強化運算，提升運算速度、促進深度參與

設計有效的強化運算的方案，強化運算體驗，積累運算經驗，幫助學生熟練掌握運算——做到算理熟練、算式規范、算法簡捷、結果準確.

（1）微專題式強化：精準施教，點點擊破（見圖13）. 關注學情與考情：圓錐曲線命題的熱點與難點，學生運算的困難點與再生點;以此為素材構建微專題，利用微專題實施精準的教學，突破運算障礙.

案例5：弦長計算類微專題的設計點.

設計點1：弦長公式優選問題：普通弦長;焦點弦;通徑.

設計點2：弦長的取值范圍問題.

設計點3：巧借弦長轉化的綜合問題.

（2）微說題式強化：思維可視化. “說”源于“思”，訓練數學思維的最優方法是“說題”. 在精心做題的基礎上，展示運算方式、解題策略和推理依據，凸顯思維可視化，并通過歸納、概括，總結出經驗性運算策略. 在運算教學中把學生引入“說題”，交流運算困惑、分享運算心得，有利于提升運算能力，培養創新思維能力、發展核心素養. 見圖14.

（3）微檢測式強化：提升效率.微檢測是指立足學情、教情、考情，針對近期（時間間隔不超過一周）講過的運算類易錯題的專題性的鞏固與檢測. 考試題量在10道題以內，時間在合適范圍以內;出題者可以是教師，也可以是學生. 通過微檢測幫助學生發現運算障礙，優化運算方案、提升運算速度.

4. 錯中反思，鞏固運算經驗、促進深度感悟

荷蘭著名的數學教育家弗賴登塔爾指出：“反思是數學思維活動的核心和動力.”美國教育家杜威指出：“真正思考的人從自己的錯誤中吸取的知識比從自己成就中吸取的知識更多，錯誤與探索相聯姻、相交合，才能孕育出真理.”運算錯誤是運算能力提升的生長點，要引導學生在錯誤中反思，透析錯誤背后所蘊含的價值，加以研究、開發與利用. 在錯誤中感悟運算真諦，在感悟中鞏固運算經驗、提升運算能力. 見圖15.

（1）知識層面類反思，彌補知識漏洞、加固運算根基. 教師與學生“個體反思+集體反思”：反思教與學，優化教與學，提升教學效益，為數學運算提供充足的養分. 對知識縱向反思、橫向反思，挖掘知識的內涵與外延，構建知識網絡，加固運算根基.

（2）思想方法類反思，優化運算策略、提升運算效益.數學思想是解決數學問題的指路燈，是運算靈感的發源地！挖掘運算錯誤背后的思想根源，揭示運算本質. 通過“一題多思”“多題對比”感悟思想、優化策略，提升運算效益.

案例6：數學思想指導下的“一題多解”的運算反思.

題8：（2014年江西省高考數學理科第15題）過點M（1，1）作斜率為-的直線與橢圓C：+=1（a>b>0）相交于點A，B. 若M是線段AB的中點，則橢圓C的離心率為__________.

目標反思：圓錐曲線的離心率，是描述曲線形狀的重要參數，很多的圓錐曲線試題都與此相關，在歷年的高考試題中頻繁出現. 解決此類問題，需要認真審核，利用題目信息、所給的數式與圖形，構造關于a，b，c三個量的等量關系或不等關系，從而找到解題方向.

解法反思：三種思想指導下的三類不同解法. （具體略）

優化反思，形成策略：點差法是處理中點弦問題的最佳策略！！

（3）經驗成果化，借鑒運算經驗、分享運算心得.美國哈佛大學校長普西曾經深刻地指出：“一個人是否具有創新能力，是‘一流人才和三流人才之間的分水嶺.”將運算類“三微”（見圖16）作為課堂教學的延伸、拓展與補充，能夠多方面地彌補課堂的不足. 設計一些適應不同層次的學生拓展、延伸的微課，這不僅是課堂教學的延伸，也是激發學生學習興趣的方法、深化教學內容的過程. 使用微課，能激起學生的思維漣漪，通過比較分析、實踐反思、微寫作等教學活動促進學生深度思考，在思考中感悟，在感悟中提升.

案例7： 學生習作《“1”與橢圓的奇妙情緣》.

“1”是數字王國中一個奇特的“人物”，他的地位無人可以取代，他的作用無人能及. 他在求最值中有著奇妙的應用.

“1”的奇妙運算：“1”具有奇妙的恒等運算性質“1×a=a（a∈R）”，這為我們求最值時進行恒等變換起到了很大的作用.

例如，已知+=1，求3x+2y的最小值.

解：3x+2y≥（3x+2y）

+

=13++≥13+2=25. 當且僅當=，即x=y=5時取等號.

“1”的奇妙變換：在三角函數中，sinα與cosα有著不變的關系，即“sin2α+cos2α=1”，這為“1”提供了一個奇妙的身份，在求最值時能發揮重要作用.

例如，已知+y2=1，求3x+2y的最小值.

解：因為+y2=1，令

=sinα，

y=cosα，所以3x+2y=6sinα+2cosα=2sin（α+β），所以-2≤3x+2y≤2.

小結：若遇到條件中有平方和為常數的求最值的問題，則可以使用換元法.

教育的目的是什么？懷特海指出：“教育的對象是有血有肉的人，教育的目的應在于激發和引導學生的自我發展之路.”以數學運算為載體，促進深度學習是實現學生自我發展的有效途徑，也是每位教師值得研究的課題！