基于極小值原理的AM T車輛起步最優協調控制策略

趙克剛，寧武林，葉 杰

（華南理工大學 汽車零部件技術國家地方聯合工程實驗室，廣州 510640）

近年來，通過對車輛起步過程中發動機與離合器間的協調控制策略的優化以改善起步動力性、經濟性和乘坐舒適性，并延長傳動系統關鍵零部件的使用壽命等，逐漸成為機械傳動領域的研究熱點［1］。

孫冬野等［2］針對機械式自動變速器（automatic mechanical transmission，簡稱AMT）車輛起步過程，提出了發動機的局部恒轉速控制策略，反映了駕駛員的起步意圖并有效地抑制了起步過程中發動機的轉速抖動。在孫冬野等研究［2］的基礎上，部分學者將模糊控制策略［3］、滑模變結構控制策略［4］及神經網絡控制策略［5］等應用于AMT、DCT（dual-clutch transmission）車輛的起步控制過程中，以獲得良好的車輛起步性能。

部分專家學者提出將最優控制理論應用于車輛起步控制策略的優化中。秦大同等［6］通過選取不同的控制、狀態變量及二次型優化目標的形式，基于線性二次型最優控制算法（linear quadratic gaussian，簡稱LQG）確定了AMT或DCT起步過程中離合器的最優接合規律。趙治國等［7］針對DCT車輛的起步過程，在發動機側采用局部恒轉速控制策略，在離合器從動側基于極小值原理獲得離合器的最優接合規律。高炳釗等［8］基于模型預測控制算法在線優化發動機和離合器的轉矩及轉速軌跡曲線，以平衡起步過程的滑摩功和沖擊度等性能指標。上述文獻［6-8］均采用數值求解方法獲得AMT或DCT車輛起步過程的最優控制規律，但數值求解計算耗時較多，不便于將其直接移植應用于車輛起步的實時控制器中。

針對AMT車輛起步的動力學過程，以滑摩功、沖擊度和控制能量等的加權和作為優化目標，在滿足駕駛員起步意圖的終端約束條件下，構建了發動機與離合器間的最優協調控制問題。并基于極小值原理將其轉化為等價的微分方程組的邊值問題，經數學推理演算可得到最優控制和狀態變量軌跡曲線的解析表達式。分析和比較基于解析求解方法和數值求解方法所得到的最優控制、狀態變量的軌跡曲線，驗證了解析求解方法更適用于實時控制系統中。基于快速原型控制器Rapid-ECU-UIM和Simulink/RTW 編譯環境，搭建了車輛起步控制的硬件在環仿真試驗平臺，提出了基于解析求解方法的車輛起步最優協調控制策略，開展了不同加權系數組合和不同節氣門開度條件下的硬件在環仿真試驗以驗證其有效性和實時性。

1 AMT車輛起步動力學過程分析

1.1 AM T車輛起步過程分析

參照文獻［9］，AMT車輛起步過程可分為準備期、半接合點前的滑摩期Ⅰ、半接合點后的滑摩期Ⅱ和轉速同步期4個階段。

1）準備期：離合器逐漸接合以消除其主、從動部分間的間隙直至開始接觸的過程；

2）半接合點前的滑摩期Ⅰ：隨著離合器壓力逐漸增大，其傳遞的摩擦轉矩也逐漸增大，但傳遞至驅動輪的驅動力矩仍小于車輛靜止阻力矩，車輛保持靜止不動；

3）半接合點后的滑摩期Ⅱ：隨著離合器傳遞的摩擦轉矩逐漸增大并克服車輛靜止阻力矩，車輛開始移動，離合器從動部分的轉速也逐漸升高至與主動部分同步；

4）轉速同步期：當離合器主、從動部分轉速完全同步之后，離合器由動摩擦狀態切換至靜摩擦狀態，且離合器壓力繼續增加直至完全接合。

在準備期和滑摩期Ⅰ這2個階段中，離合器的接合快慢并不會引起車輛的縱向沖擊，為滿足快速起步的要求，應在發動機不熄火的前提下盡快地接合離合器。在滑摩期Ⅱ，離合器接合速度較大，會引起發動機轉速波動較大且造成較大的車輛沖擊，影響起步平順性；離合器接合速度較慢，則會造成起步緩慢且延長離合器滑摩時間，增大離合器的滑摩功從而降低離合器使用壽命。在轉速同步期，離合器主、從動部分轉速同步且離合器完全接合，故并不會因離合器的滑摩產生滑摩功，則可在滿足沖擊度的約束條件下盡快地將車速提升至目標車速，完成整個起步過程。

基于AMT起步過程4個階段的機理分析可知，半接合點后的滑摩期Ⅱ中發動機與離合器間的協調控制是影響車輛動力性、經濟性等起步品質的關鍵。

1.2 AMT車輛起步動力學模型

為便于AMT車輛起步控制策略的研究，采用集中參數建模，簡化后所建立的AMT起步動力學模型如圖1所示［10］。

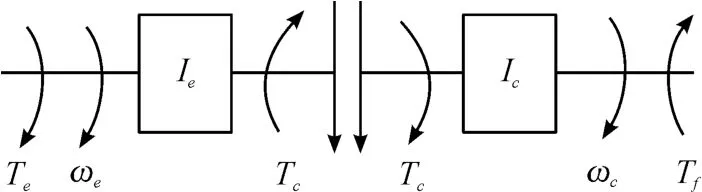
圖1 AMT車輛起步動力學模型示意圖

圖1中符號定義如下：Ie為發動機、離合器主動部分等部件等效至發動機端的當量轉動慣量；Ic為離合器從動部分、變速器、主減速器、車輪及車身等部件等效至離合器從動端的當量轉動慣量；Te為發動機輸出轉矩；Tc為離合器傳遞轉矩；Tf為等效至離合器從動端的車輛行駛阻力矩；ωe為發動機端轉速；ωc為離合器從動端轉速。

AMT車輛起步過程半接合點后的滑摩期Ⅱ中傳動系統的動力學方程為：

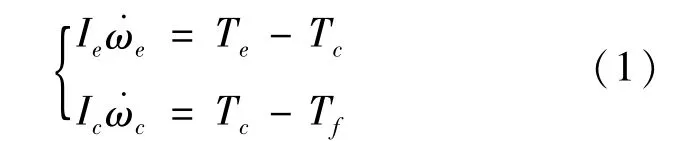
離合器的傳遞轉矩Tc可表示為［11］：

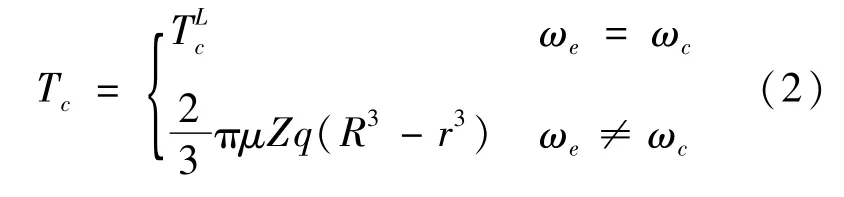
式中：μ為離合器摩擦片間的摩擦系數；z為摩擦片個數；R和r為摩擦片的外徑和內徑；q為執行機構作用于摩擦片的單位面積壓力；TLc為離合器完全接合時所傳遞的慣性力矩。

等效至離合器從動端的車輛行駛阻力矩為：

其中，滾動阻力、空氣阻力和坡度阻力為：

式中：rw為車輪滾動半徑；in為變速器起動擋位的傳動比；i0為主減速器的傳動比；m為車質量；g為重力加速度；f為滾動阻力系數；θ為坡度角；CD為空氣阻力系數；A為車輛的迎風面積；v為車速。

2 起步最優協調控制問題

2.1 起步最優協調控制問題的描述

選取發動機轉速、離合器從動端轉速和離合器傳遞轉矩等作為狀態變量，則狀態變量X可表示為：

選取發動機轉矩和離合器轉矩變化率作為控制變量，則控制變量U可表示為：

則可將起步動力學方程（1）轉換成狀態方程的形式：

其中，

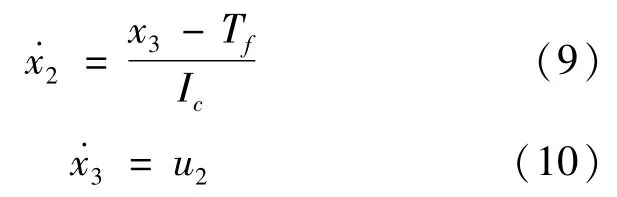
為適應駕駛員的起步意圖，以駕駛員目標節氣門開度下發動機輸出最大轉矩時所對應的轉速為發動機目標轉速。因此，在離合器主、從動部分的轉速同步時刻（即滑摩期Ⅱ的結束時刻），狀態變量x1需滿足如下邊界條件：

由離合器傳遞轉矩連續變化所引起的車輛沖擊度j可表示為：

由離合器摩擦片摩擦所產生的滑摩功W可表示為：

式中：t0和tf分別為滑摩期Ⅱ的開始和結束時刻。

為改善起步過程中離合器的使用壽命、起步平順性及控制器能耗等起步性能，選取滑摩功、沖擊度平方和控制能量消耗等的加權和作為優化目標J，其表達式為：

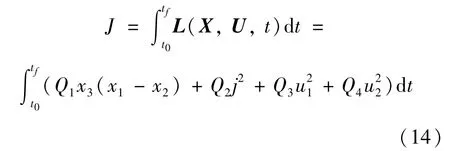
式中：Q1、Q2、Q3、Q4分別為優化目標中滑摩功、沖擊度平方項、控制變量u1和u2的平方項的加權系數。

2.2 起步最優協調控制問題的求解

針對起步最優協調控制問題，引入拉格朗日乘子向量λ=［λ1，λ2，λ3］T，并構造廣義目標泛函：

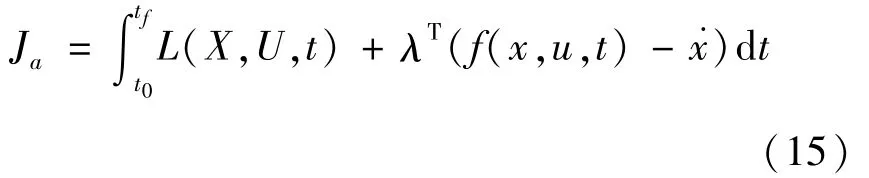
則Hamilton函數H（X，U，λ，t）為：

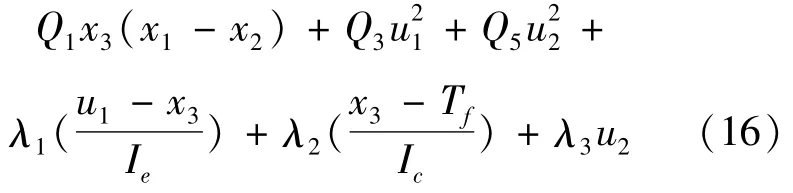
基于極小值原理可確定最優控制、狀態及協狀態變量需滿足的最優性一階必要條件，即狀態方程（8）～（10）、協狀態方程（17）～（19）和控制方程（20）～（21）。

協狀態方程：

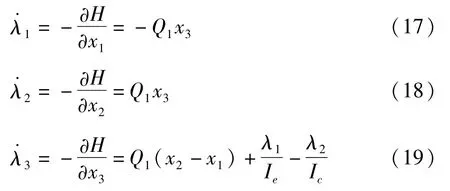
控制方程：

在初始時刻t0引入初始邊值條件：

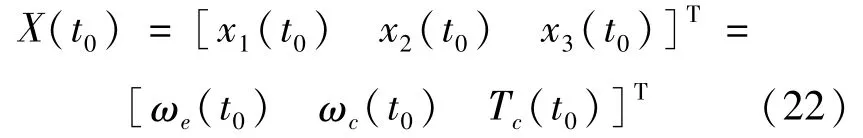
式中，we（t0）為發動機怠速工況下的初始轉速；wc（t0）為零；Tc（t0）為等效至離合器從動端的車輛靜止行駛阻力矩。

在結束時刻tf引入終了邊值條件：

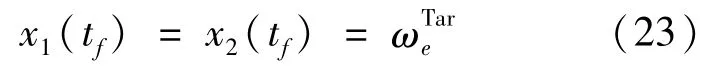
同時，引入協狀態變量的橫截條件：

2.2.1 邊值問題的解析求解方法

針對基于極小值原理轉化而來的微分方程組邊值問題（即式（8）～（10））和式（17）～（24））進行數學推導求解，以獲得最優控制、狀態變量軌跡的解析表達式。

對式（19）進行一階求導，并將式（8）（9）（17）（18）代入可得：

對式（25）進行一階求導，并代入式（17）可得：

對式（26）進行一階求導，并將式（10）和（21）代入可得：

式（27）是關于λ3的4階微分方程，可得其解析解為：

式中：C1、C2、C3、C4為待定常系數；k1的表達式如式（29）所示。

式中，k2的表達式為：

以式（28）所示的最優協狀態變量λ*3的解析表達式為突破口，可逐一求解得到最優控制變量u*1、u*2，最優狀態變量x*1、x*2、x*3和最優協狀態變量λ1*和λ*2的解析表達式。具體推導過程如式（31）～（40）所示。

將式（28）代入式（21）可得u2*的解析表達式：

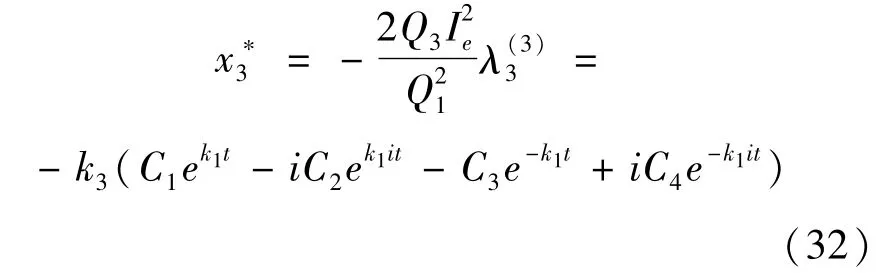
根據式（20）即可得u*1的解析表達式：

聯合式（18）和式（32）可得λ*2的解析表達式：

式中，C5為待定系數。

將式（32）代入式（9）可得x*2的解析表達式：

式中，

聯合式（19）（28）（35）和（36）可解得x*1的解析表達式：

式中，

通過將邊值條件（22）～（23）、橫截條件（24）代入即可得到待定系數C1、C2、C3、C4、C5的值。

2.2.2 邊值問題的數值求解方法

打靶法是求解微分方程組邊值問題的一種有效數值求解方法，其實質是將微分方程組的邊值問題轉化為初值問題進行求解，并且通過不斷迭代調整未知的初始條件，使迭代后的計算末值滿足給定的終了時刻邊值條件。基于打靶法對前文中的微分方程組邊值問題開展數值求解的過程如圖2所示。結合已有的狀態變量初值條件和協狀態變量未知初始條件的猜測值，通過狀態方程、協狀態方程和控制方程等進行數值積分計算得到狀態變量與協狀態變量的末值，并將計算末值代入終了時刻的邊界條件及橫截條件中計算比較，若偏差Δ在允許誤差ε的范圍內，則結束迭代過程；若偏差Δ超出允許誤差ε的范圍，則通過偏微商矩陣更新協狀態變量初始條件的猜測值并重復上述過程。

圖2 打靶法求解過程框圖

2.3 解析解與數值解比較

以某款配備了5速AMT的中型轎車為研究對象對其起步過程進行研究，其傳動系統的主要參數見表1。

表1 傳動系統的主要參數

在其起步過程中最優控制和狀態變量軌跡曲線的求解過程中，優化目標中各項加權系數的選取是一個工程性很強的問題，一般依賴于專家經驗及實車標定試驗后的結果進行調整選取。基于經驗，在節氣門開度為20%下，選取各加權系數為Q1=1、Q2=1、Q3=8和Q4=6。

在Matlab R2013b的編譯環境下分別采用解析和數值求解方法求得20%節氣門開度下的起步過程半接合點后的滑摩期Ⅱ中的最優軌跡曲線，如圖3所示。

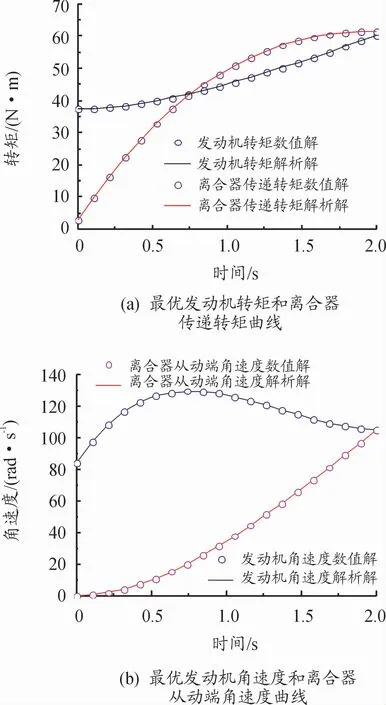
圖3 最優控制軌跡解析解與數值解

離合器傳遞轉矩隨著接合壓力的逐漸增加而逐漸增大，離合器從動端的轉速也由零開始逐漸增大至與發動機轉速同步（即車速由零開始逐漸增大至起步完成）。在前半部分，因發動機轉矩仍大于離合器傳遞轉矩，故發動機轉速仍保持上升趨勢；而在后半部分，為減小離合器的滑摩功，離合器傳遞轉矩迅速超過發動機轉矩，使發動機轉速逐漸減小至與離合器從動端轉速同步。對比圖3中2種求解方法得到的最優軌跡曲線可知，兩者的最大相對誤差不超過0.2%。基于解析法和數值法求解計算最優軌跡曲線的時長分別為0.006 4 s和0.314 s，前者是后者的1/49，因此基于解析法的最優軌跡曲線更適于實時控制系統的應用。

3 AMT車輛起步硬件在環仿真試驗

基于快速原型控制器Rapid-ECU-UIM 和Matlab/Simulink/RTW 平臺搭建了AMT車輛起步的硬件在環仿真試驗平臺，并開展了不同加權系數組合及不同節氣門開度下的AMT起步仿真試驗以驗證基于解析解的起步最優協調控制策略的有效性和實時性。

3.1 AMT起步的硬件在環仿真系統

基于快速原型控制器Rapid-ECU-UIM 和Matlab/Simulink/RTW 平臺所搭建的AMT起步硬件在環仿真平臺包括硬件和軟件兩部分。其中，硬件部分主要由快速原型控制器Rapid-ECUU1M、PC機、數據采集卡PCI-6024E等組成；軟件部分主要包括AMT車輛起步的整車實時仿真模型、快速原型控制器中的起步最優協調控制模型及RTW 目標環境等。AMT車輛起步的硬件在環仿真系統的結構框圖及實物圖如圖4、5。

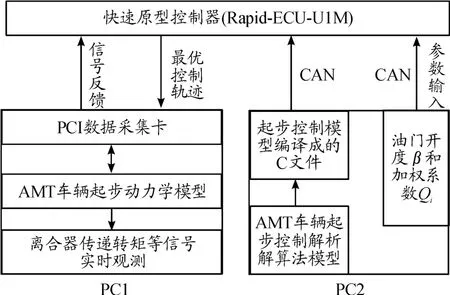
圖4 硬件在環仿真試驗系統結構框圖

圖5 硬件在環仿真試驗系統的實物圖

在AMT起步的硬件在環仿真試驗中，PC2將基于解析求解方法的AMT起步最優控制模型編譯成C文件并通過CAN總線下載至快速原型控制器Rapid-ECU-UIM中，將節氣門開度和加權系數等作為起步控制器的輸入參數；Rapid-ECU-UIM將求解得到的最優控制和狀態變量的軌跡曲線通過PCI-6024E采集卡輸入至PC1中所構建AMT車輛起步動力學模型作為控制輸入；最后將仿真計算得到的數據反饋至控制器。

3.2 不同加權系數下的硬件在環仿真

在AMT車輛起步最優協調控制策略的設計中，優化目標中滑摩功、沖擊度及控制能量等項的加權系數的不同體現了控制策略優化的側重方向，會引起起步性能的變化。本小節通過保持優化目標中的加權系數Q2、Q3、Q4（即沖擊度平方和控制能量等項的加權系數）恒定且為1、8及6，通過改變Q1（滑摩功的加權系數）以分析優化目標中加權系數的選取對起步性能的影響。Q1分別取0.6、0.8和1的硬件在環仿真試驗結果如圖6所示。

如圖6（a）和（b）所示，不同加權系數下，發動機轉矩、離合器傳遞轉矩變化平穩，無明顯突變。且在前半階段發動機轉矩明顯大于離合器傳遞轉矩，發動機轉速迅速上升；在后半階段離合器傳遞轉矩逐漸上升至超過發動機轉矩，則發動機轉速迅速降低直至與離合器從動端轉速同步以有效地減小滑摩功。如圖6（c）和（d）所示，隨著Q1的逐漸增大，即優化目標中滑摩功權重的逐漸增大，沖擊度的最大幅值逐漸增大，而總滑摩功則逐漸減小，具體數據見表2。

表2 不同加權系數下的沖擊度最大幅值與滑摩功

3.3 不同節氣門開度下的硬件在環仿真

在節氣門開度分別為20%和40%下進行緩起步與快起步的硬件在環仿真，結果如圖7所示。

圖6 不同加權系數下的AMT起步仿真試驗曲線

圖7 不同節氣門開度下的AMT起步仿真試驗曲線

如圖7（a）和（b）所示，相比于20%節氣門開度，40%節氣門開度下起步要求更快，則發動機需求轉矩更大，且目標角速度也隨之增大。在節氣門開度20%和40%下發動機轉速與離合器從動端轉速分別在2 s和1.55 s完成同步，此時發動機目標角速度分別為104.7、146.5 rad/s。如圖7（c）和（d）所示，節氣門開度20%和40%下沖擊度均維持在較低水平，沖擊度最大幅值分別為1.89、3.23 m/s3，均小于10 m/s3；起步過程的滑摩功分別為5.78、10.49 kJ。

4 結論

1）針對AMT車輛起步的應用要求，基于極小值原理推導了起步過程中最優控制和狀態變量的解析表達式，提出了基于解析求解方法的發動機與離合器的起步最優協調控制策略并應用于實時控制中，對于進一步探索起步優化方法有重要參考價值。

2）基于快速原型控制器Rapid-ECU-U1M和Matlab/Simulink/RTW 軟件平臺構建了AMT起步的硬件在環仿真試驗平臺，并在不同加權系數組合和不同節氣門開度下開展了AMT起步仿真，驗證了所提出的最優協調控制策略能滿足實時性要求。