全捷聯(lián)導(dǎo)引頭寄生回路穩(wěn)定裕度分析及校正網(wǎng)絡(luò)設(shè)計*

楊泗智

（西北工業(yè)大學(xué)航天學(xué)院，西安 710072）

0 引言

相對于傳統(tǒng)平臺式導(dǎo)引頭，全捷聯(lián)導(dǎo)引頭用數(shù)學(xué)平臺隔離彈體擾動，并從中提取出視線角速度［1］。全捷聯(lián)導(dǎo)引頭在提取視線角速度的過程中，需要同時利用導(dǎo)引頭量測的誤差角信息和彈上慣導(dǎo)系統(tǒng)量測的彈體姿態(tài)角信息，當探測器與慣性器件輸出信息的刻度尺或動力學(xué)不一致時，將會使補償后的視線角存在一定的誤差，該誤差在制導(dǎo)系統(tǒng)中增加了寄生回路，影響制導(dǎo)系統(tǒng)數(shù)學(xué)平臺的隔離度，同時該寄生回路對全捷聯(lián)制導(dǎo)系統(tǒng)的穩(wěn)定性和有效導(dǎo)航比會有顯著影響［2-3］。

目前國內(nèi)外學(xué)者在寄生回路對制導(dǎo)控制系統(tǒng)的穩(wěn)定性和制導(dǎo)精度影響方面的研究已經(jīng)做了大量工作，如：王嘉鑫等［4］利用李雅普諾夫函數(shù)法分析了制導(dǎo)系統(tǒng)的一致漸進穩(wěn)定條件，研究了隔離度對比例導(dǎo)引制導(dǎo)穩(wěn)定性的影響。李富貴等［5-6］采用勞斯判據(jù)和系數(shù)凍結(jié)法研究了剩余飛行時間、制導(dǎo)參數(shù)、刻度尺偏差對制導(dǎo)穩(wěn)定性的影響，利用伴隨函數(shù)法研究了刻度尺偏差對脫靶量的影響。鄢琴濤等建立了引入末制導(dǎo)回路的隔離度寄生回路模型，得出了基于不同末制導(dǎo)剩余時間下的隔離度臨界幅值。針對常用誤差模型下隔離度正反饋幅值的影響，提出了一種引入制導(dǎo)回路的末制導(dǎo)剩余時間值的計算方法［7］。

綜上，在寄生回路分析方面，目前主要集中在制導(dǎo)控制系統(tǒng)的穩(wěn)定性和制導(dǎo)精度影響方面展開研究，而對于寄生回路本身的穩(wěn)定裕度分析以及其校正控制方面未見相關(guān)研究。

本文在頻域內(nèi)分析了刻度尺誤差和動力學(xué)延時對寄生回路穩(wěn)定性的影響，利用幅相裕度確定寄生回路的刻度尺誤差和動力學(xué)延時允許的變化范圍，在時域內(nèi)對邊界條件進行了驗證，同時分析了刻度尺誤差對有效導(dǎo)航比的影響。當寄生回路的參數(shù)不能滿足穩(wěn)定性要求時，利用超前校正網(wǎng)絡(luò)進行補償設(shè)計，通過校正網(wǎng)絡(luò)保證寄生回路的穩(wěn)定裕度，在滿足穩(wěn)定裕度的基礎(chǔ)上，通過調(diào)整增益補償寄生回路和校正網(wǎng)絡(luò)參數(shù)對有效導(dǎo)航比的影響，使其滿足制導(dǎo)系統(tǒng)穩(wěn)定性和比例導(dǎo)引系統(tǒng)的要求。

1 寄生回路模型分析

圖1 全捷連導(dǎo)引頭制導(dǎo)控制回路

其中，Vc為彈目接近速度，tgo為剩余飛行時間，Tf為濾波器時間常數(shù)，N 為導(dǎo)航比，Tm為彈體震蕩周期，μm為彈體運動阻尼系數(shù)，Ta為攻角時間常數(shù)。由于探測器的光電測量裝置的速度非常快，其動力學(xué)滯后可以忽略，同時探測器的輸出與視線角成線性關(guān)系，因此，在制導(dǎo)回路中可以不考慮捷聯(lián)探測器的動力學(xué)延時，可以令Gs（s）=1。而對角速率陀螺要考慮動力學(xué)延時的影響，同時由于探測器和角速率陀螺在測量過程中存在刻度尺誤差，造成數(shù)學(xué)平臺不能夠完全補償彈體擾動，從而構(gòu)成寄生回路。在不考慮噪聲的情況下，綜合彈體擾動和角速率陀螺補償及探測器的傳遞函數(shù)，對制導(dǎo)控制回路進行簡化得到寄生回路的模型如圖2 所示。

圖2 寄生回路結(jié)構(gòu)圖

由于1-Gg（s）的傳遞函數(shù)主要由陀螺與探測器的刻度尺誤差和動力學(xué)延時構(gòu)成，可以令

為了對寄生回路的穩(wěn)定性進行分析，這里主要在頻域內(nèi)研究，在頻域內(nèi)當由n 個環(huán)節(jié)串聯(lián)時，可以得到開環(huán)傳遞函數(shù)為：

其中，對數(shù)的復(fù)頻特性為：

對于全捷連導(dǎo)引頭采用角速率陀螺進行反饋，捷聯(lián)導(dǎo)引頭探測器的傳遞函數(shù)用Gs（s）表示，角速率反饋系統(tǒng)的傳遞函數(shù)用Gg（s）表示，采用比例導(dǎo)引控制的全捷聯(lián)制導(dǎo)控制系統(tǒng)的原理如圖1 所示。

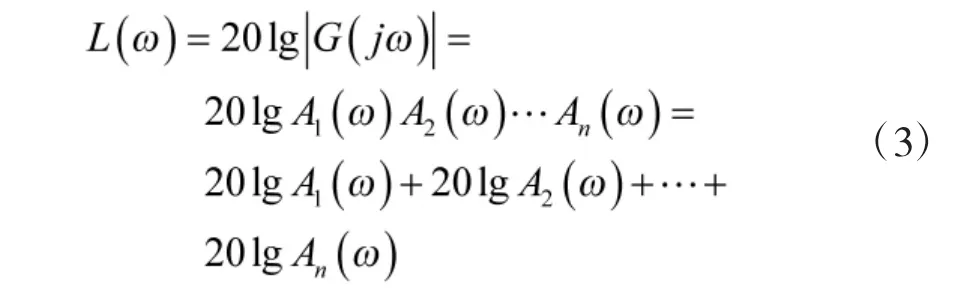
對數(shù)的相頻特性為：

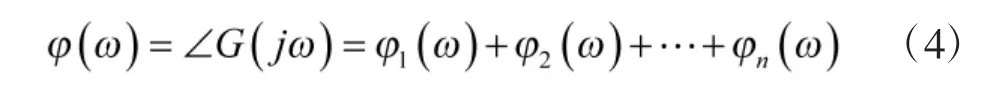
2 寄生回路穩(wěn)定性分析

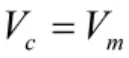
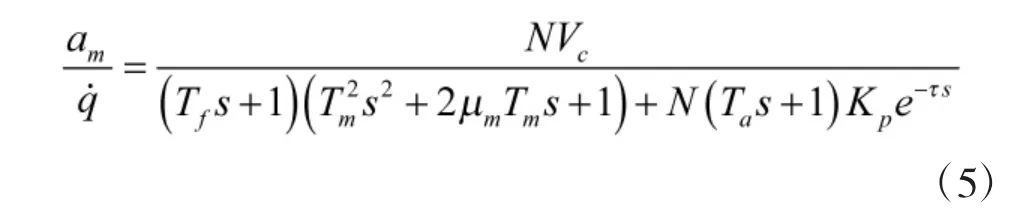
寄生回路的開環(huán)傳遞函數(shù)為：

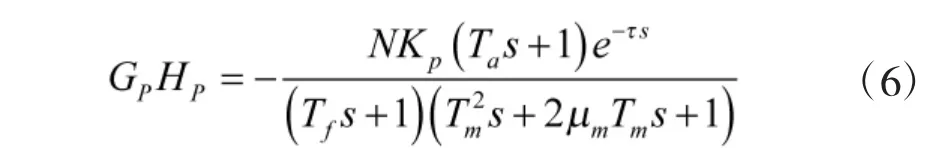
開環(huán)傳遞函數(shù)的幅值函數(shù)和相位函數(shù)分別為：

由式（7）和式（8）可以看出：在彈體動力學(xué)和導(dǎo)航比參數(shù)確定的情況下，寄生回路的穩(wěn)定性及其裕度主要由刻度尺誤差Kp和動力學(xué)延時決定，并且相互獨立。

制導(dǎo)控制參數(shù)的取值如表1 所示：

表1 寄生回路參數(shù)取值

在頻域內(nèi)利用bode 圖可以得到寄生回路開環(huán)系統(tǒng)的幅值和相位隨頻率的變化曲線如圖3 所示。可以看出寄生回路是穩(wěn)定的，其中剪切頻率為ωCR=19 rad/s，穿越頻率ωg=37.8 rad/s，幅值裕度：Gm=12.4 dB，相角裕度：φm=33.2°。

2.1 頻域內(nèi)寄生回路的穩(wěn)定性分析

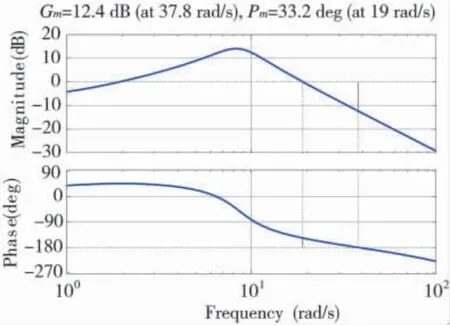
圖3 寄生回路開環(huán)傳遞函數(shù)的bode 圖

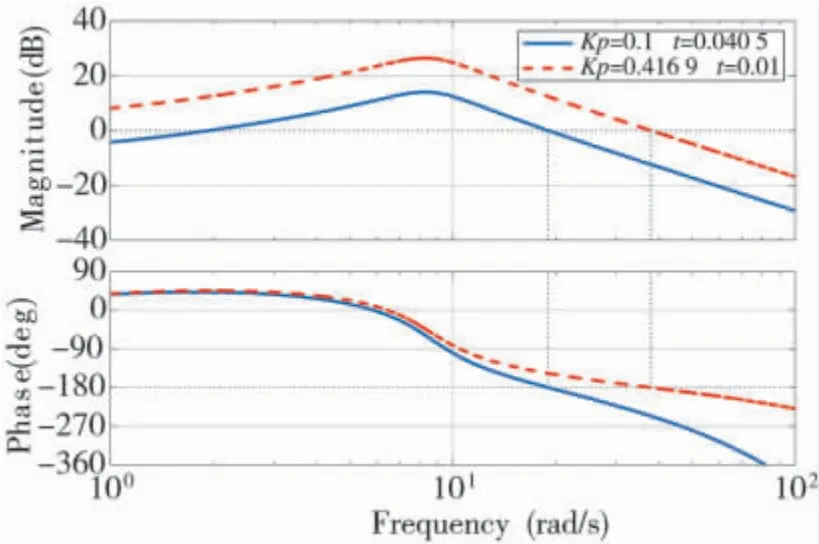
圖4 刻度尺誤差和動力學(xué)延時邊界狀態(tài)的bode 圖

由圖4 可以看出，刻度尺誤差和動力學(xué)延時處于邊界時寄生回路處于臨界穩(wěn)定狀態(tài)。

2.2 時域內(nèi)寄生回路穩(wěn)定邊界的驗證

當刻度尺誤差和動力學(xué)延時處于邊界狀態(tài)時，在時域內(nèi)對寄生回路閉環(huán)系統(tǒng)進行仿真，可以得到階躍響應(yīng)曲線如圖5 所示：

圖5 邊界狀態(tài)的單位階躍響應(yīng)函數(shù)

由圖5 可以看出，當刻度尺誤差或動力學(xué)延時處于臨界穩(wěn)定邊界時，單位階躍響應(yīng)也處于臨界穩(wěn)定狀態(tài)，驗證了刻度尺誤差和系統(tǒng)延時臨界值的正確性，同時也可以看出刻度尺誤差同時影響制導(dǎo)控制回路的穩(wěn)態(tài)誤差。

3 寄生回路對有效導(dǎo)航比的影響

為了分析寄生回路對導(dǎo)航比的影響，對寄生回路引起的制導(dǎo)控制系統(tǒng)的穩(wěn)態(tài)特性進行分析，得到控制過載與視線角變化率的傳遞函數(shù)如下：

由式（11）可知：對于負反饋時有效導(dǎo)航比小于比例導(dǎo)引系數(shù)，正反饋時有效導(dǎo)航比大于比例導(dǎo)引系數(shù)，刻度尺誤差對導(dǎo)航比有影響，因此，在選擇導(dǎo)航比的時候要考慮刻度尺誤差的影響，在控制系統(tǒng)設(shè)計時需要對其進行補償。

4 增加超前校正網(wǎng)絡(luò)+增益控制

為了補償寄生回路對制導(dǎo)控制系統(tǒng)的影響，這里采用超前校正網(wǎng)絡(luò)+增益控制。增加校正網(wǎng)絡(luò)+增益控制后的制導(dǎo)控制回路如圖6 所示：

圖6 增加校正網(wǎng)絡(luò)+增益控制的制導(dǎo)控制回路

其中，超前校正網(wǎng)絡(luò)傳遞函數(shù)為：

α 稱為分度系數(shù)，T 為時間常數(shù)，根據(jù)超前校正網(wǎng)絡(luò)的性質(zhì)可以得到最大超前角頻率為：

最大超前角為：

為使有效導(dǎo)航比與比例導(dǎo)引系數(shù)一致，需要進行增益調(diào)節(jié)。根據(jù)式（10）可知，增加校正網(wǎng)絡(luò)和增益控制后的系統(tǒng)穩(wěn)態(tài)值為：

為分析方便這里按照幅值裕度：Gm≥10 dB，相角裕度：φm≥30°對兩種穩(wěn)定邊界值進行設(shè)計。

1）當Kp=0.416 9，=0.01 s 時，其中剪切頻率為ωCR=37.8 rad/s，為了滿足幅值和相位裕度的要求，令φm≥35°，根據(jù)式（14）算得α=3.690 4。令ωm=ωCR，由式（13）算得：T=0.013 8 s，令Kc=1，校正剪切頻率為ωCR=24.5 rad/s，幅值裕度為13.9 dB，相角裕度為52.3°，通過超前校正網(wǎng)絡(luò)補償滿足穩(wěn)定裕度要求。增加校正網(wǎng)絡(luò)前后的伯德圖變化如圖7 所示：

圖7 校正網(wǎng)絡(luò)補償刻度尺誤差的伯德圖

同時，由式（15）得到增益值：K=5.358，寄生回路在校正網(wǎng)絡(luò)+增益控制和無補償控制及與無寄生回路影響的比例導(dǎo)引控制，在單位階躍響應(yīng)條件下的對比如圖8 所示：

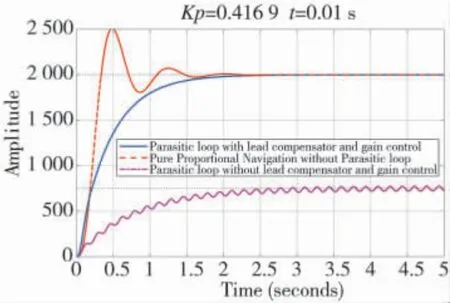
圖8 刻度尺誤差條件下校正網(wǎng)絡(luò)+增益控制與其他狀態(tài)的對比

圖8 可以看出通過增加校正網(wǎng)絡(luò)+ 增益控制可以滿足穩(wěn)定度要求，同時有效導(dǎo)航比與比例導(dǎo)引控制一致，可以消除寄生回路刻度尺誤差對制導(dǎo)控制系統(tǒng)的影響。

2）當Kp=0.1，=0.040 5 s 時，根據(jù)前面的分析取α=3.690 4，由穿越頻率ωg=19 rad/s，令ωm=ωg，可以得到T=0.027 4s，令Kc=1，校正后穿越頻率為ωg=10.901 8 rad/s，相角裕度為86.99°，幅值裕度為14.6 dB，滿足穩(wěn)定裕度要求，增加校正網(wǎng)絡(luò)前后的伯德圖變化如圖9 所示。

圖9 動力學(xué)延時補償校正網(wǎng)絡(luò)伯德圖

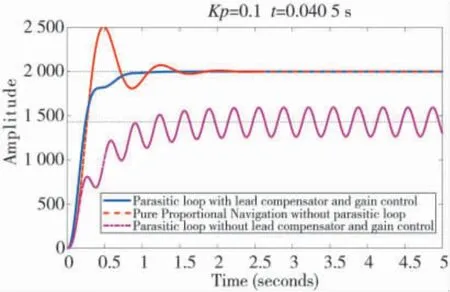
圖10 動力學(xué)延時條件下校正網(wǎng)絡(luò)+增益控制與其他狀態(tài)的對比

同樣由式（15）得到增益值：K=4.090 4，寄生回路在校正網(wǎng)絡(luò)+增益控制和無補償控制及與無寄生回路影響的比例導(dǎo)引控制在單位階躍響應(yīng)條件下的對比如圖10 所示。

圖10 可以看出，通過增加校正網(wǎng)絡(luò)+增益控制滿足穩(wěn)定度，要求同時有效導(dǎo)航比與比例導(dǎo)引控制一致，可以消除寄生回路動力學(xué)延時對制導(dǎo)控制系統(tǒng)的影響。

對于刻度尺誤差和動力學(xué)延時同時超出臨界值的不穩(wěn)定狀態(tài)采用同樣的處理可以進行校正，從而將寄生回路引起不穩(wěn)定系統(tǒng)校正為穩(wěn)定系統(tǒng)，同時通過增益控制滿足比例導(dǎo)引系統(tǒng)有效導(dǎo)航比的要求。

5 結(jié)論

本文通過對捷聯(lián)導(dǎo)引頭制導(dǎo)控制回路的模型分析，建立了寄生回路的數(shù)學(xué)模型及其簡化形式，在頻域內(nèi)利用幅值和相角裕度計算出寄生回路的刻度尺誤差和動力學(xué)延時允許的變化范圍，在時域內(nèi)對邊界條件進行了驗證，驗證了邊界條件即為寄生回路的臨界穩(wěn)定狀態(tài)。分析了刻度尺誤差對有效導(dǎo)航比的影響，得到在穩(wěn)態(tài)條件下負反饋有效導(dǎo)航比小于比例導(dǎo)引系數(shù)，正反饋有效導(dǎo)航比大于比例導(dǎo)引系數(shù)。當寄生回路的參數(shù)不能夠滿足穩(wěn)定裕度要求時，利用超前校正網(wǎng)絡(luò)+增益控制進行補償設(shè)計，通過校正網(wǎng)絡(luò)設(shè)計保證寄生回路的穩(wěn)定裕度，同時通過增益控制補償寄生回路開環(huán)增益對有效導(dǎo)航比的影響，使其滿足制導(dǎo)系統(tǒng)穩(wěn)定裕度和比例導(dǎo)引系統(tǒng)的要求。