通用脈沖雷達信號仿真軟件設計與實現*

張華杰

（新鄉學院物理與電子工程學院，河南 新鄉 453000）

0 引言

雷達系統在軍事和民用領域都有著很廣泛的影響，長期以來我國的雷達制造水平有了長足的發展，但在系統的仿真領域起步較晚，而且缺乏統一的規劃。隨著雷達系統的日益復雜，進行雷達系統軟件仿真的難度也越來越大，軟件系統的規模和復雜性也日益增加。

雷達信號仿真系統的設計與實現是雷達信號理論工程實現的重要途徑之一，雷達系統仿真就是通過建立雷達系統模型，利用軟件和硬件的手段復現雷達系統的動態工作過程。它仿真的對象是雷達系統，包括雷達本身（硬件及軟件），雷達回波和回波環境；仿真的方式是復現蘊含雷達回波場景信息的雷達回波信號及其傳遞、處理的動態過程，從時間關系上看，就是重現一個隨機的時間序列。由于雷達發射波形不僅決定了信號處理方法，而且直接影響系統的分辨力、測量精度以及抑制雜波能力等潛在性質。于是，波形設計就成了雷達系統最佳綜合的重要內容，逐漸形成現代雷達理論的重要分支。綜上所述，雷達信號理論的形成與發展，目的在于提高雷達信號傳輸的可靠性和有效性。

1 典型雷達的脈沖信號

將幅度A 歸一化為1，得到單載頻矩形脈沖信號的模糊函數表達式

以上三式可合并為

取模得到

線性調頻矩形信號表示為

線性調頻矩形脈沖信號，其載頻在脈沖寬度內按線性規律變化，即用對載頻進行線性調制的方法展寬信號的頻譜，使其相位具有色散特性。同時，在發射信號的峰值功率Pi受限的情況下，為了充分利用發射機的功率，通常采用矩形寬脈沖的信號包絡。

其中，調頻帶寬

Δf 成為調制頻偏。用對應的角頻率表示可以寫為ΔΩ=2πΔf，故調頻斜率為

若信號的載波中心角頻率為Ω0=2πf0，則線性調頻矩形脈沖信號的角頻率變化規律為

因而，信號的瞬時相位φ（t）為

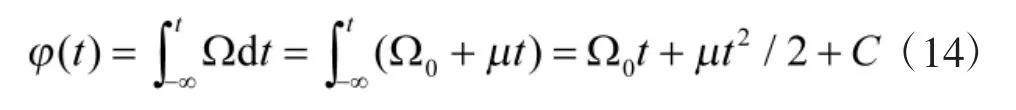
這樣，線性調頻矩形脈沖信號的表達式為

其中，μ=2πK。為了方便計算分析，將信號s（t）用復數形式表示為

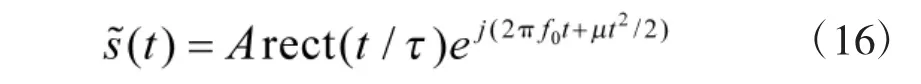
對信號s（t）進行傅里葉變換，得信號的復頻譜函數為

則信號的頻譜函數表達式為

1.1 幅頻函數及特性

線性調頻矩形脈沖信號的幅頻函數為

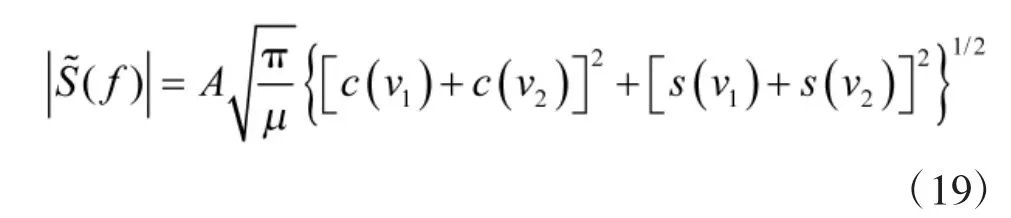
當f=f0時，可得

當D>>1 時，有c（v1）=c（v2）≈0.5，s（v1）=s（v2）≈0.5

所以，可得幅頻函數為

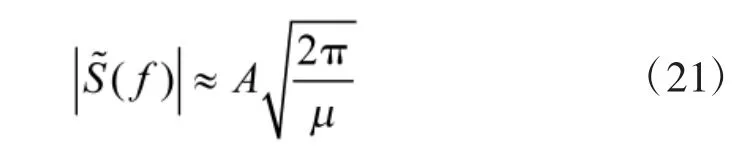
當f=f0+Δf/2 時，可得v1= 2D ，v2=0

當D>>1 時，有c（v1）=c（v2）≈0.5，s（v1）=s（v2）≈0

可得，（22）

即幅度頻譜為中心角頻率f=f0時的一半。

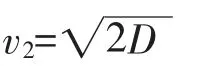
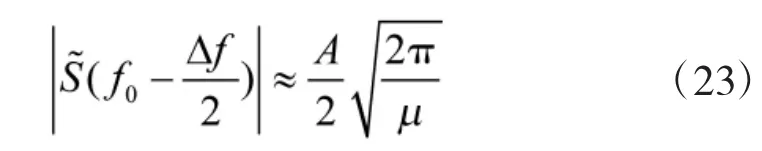
即幅度頻譜也為中心角頻率f=f0時的一半。

當壓縮比D 不同時，幅度頻譜的特性也隨之變化。D 值越大，則幅頻特性在（f0-Δf/2）～（f0+Δf/2）之間越平坦，在這個頻帶之外幅度下降越快，信號的能量主要集中在此頻帶范圍內。計算結果表明，當D=10 時，則95%的信號能量包含在此頻帶范圍內；當D=100 時，則98%的信號能量包含在此頻帶范圍內。由于實際使用的線性調頻矩形脈沖信號通常均滿足D=B>>1，故其幅頻特性很接近矩形，所以可近似表示為，

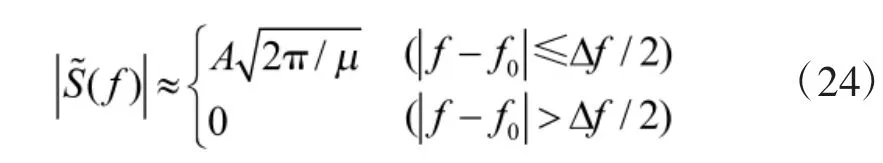
1.2 相頻函數及特性

線性調頻矩形脈沖信號的幅頻函數為

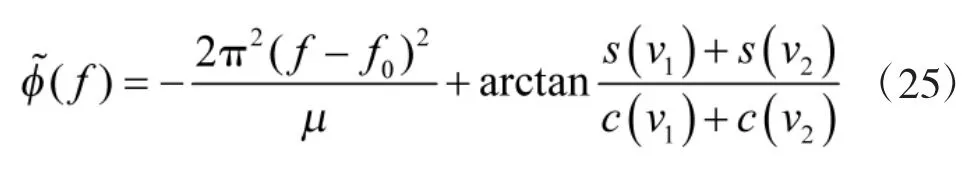
它包含平方相位項和剩余相位項兩部分，反映了信號的相頻特性。

其中，平方相位項為

剩余相位項為

因而

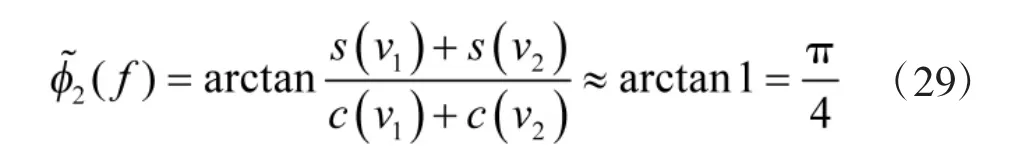
當D>>1 時，線性調頻矩形脈沖信號的相頻函數可近似表達為

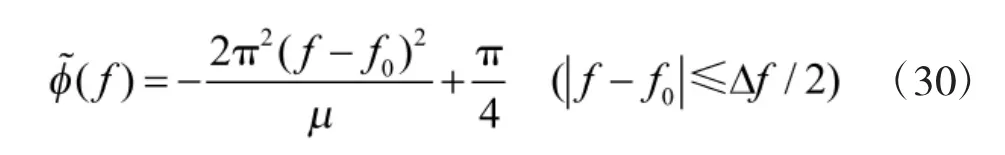
這樣，當壓縮比D 很大時，線性調頻矩形脈沖信號的相頻函數可表示為

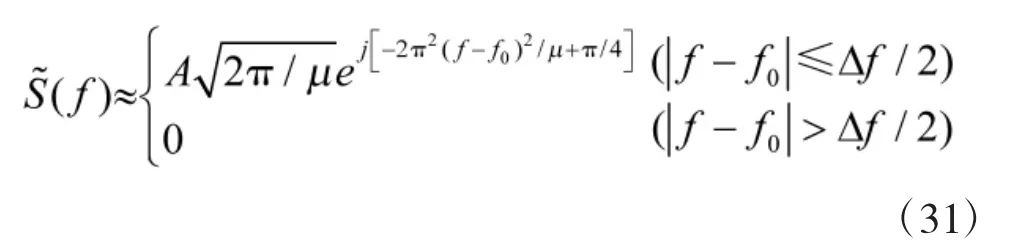
綜上討論，線性調頻矩形脈沖信號具有如下主要特點：

2）線性調頻矩形脈沖信號具有近似矩形的幅頻特性，D 值越大，其幅頻特性越接近矩形，頻譜寬度近似等于信號的調頻寬度B=Δf。

3）線性調頻矩形脈沖信號具有平方律的相頻特性，在設計匹配壓縮濾波器時要考慮到相位頻譜函數的這一特性。

將線性調頻矩形脈沖信號的幅度A 歸一化為1。根據模糊函數的性質4，時域引入平方相位項對模糊函數的影響，線性調頻矩形脈沖信號的模糊函數可由單載頻矩形脈沖信號函數按下列關系

直接導出。可得

于是得到

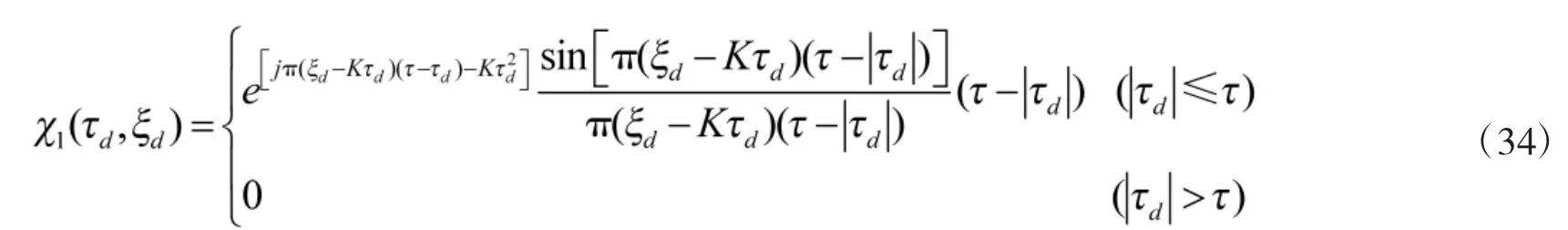
取模得到

偽隨機二相編碼信號的復包絡為

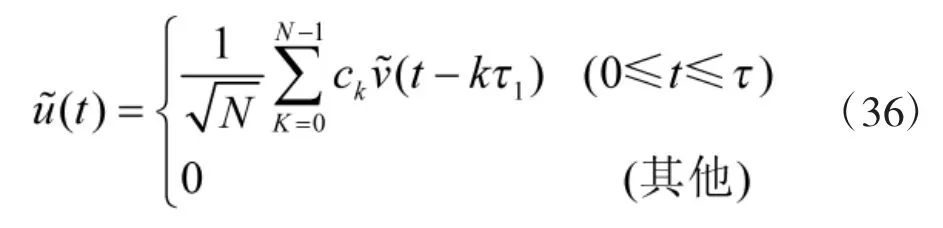
偽隨機二相編碼信號的表達式為

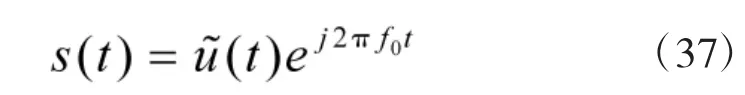
偽隨機相位編碼信號的復信號表示為

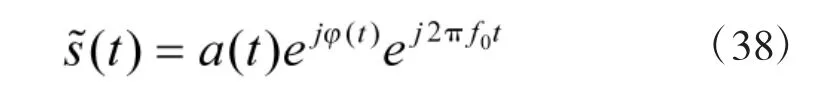
式中，φ（t）為相位調制函數。

對二項編碼信號來說，φ（t）只取0、π 兩個數值，可用二進制相位序列{φk=0、π}表示，也可用二進制數字序列{ck=ejφk}=±1 表示。如果二相編碼信號的包絡為矩形，即

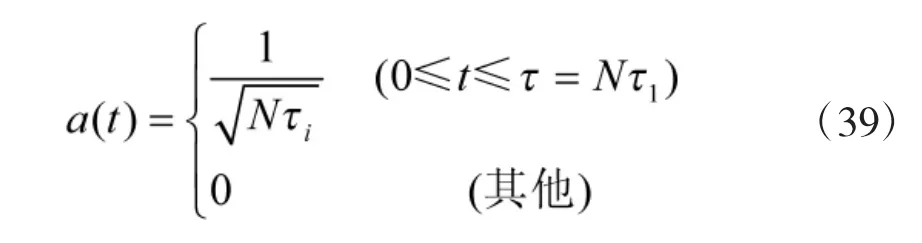
則二相編碼信號的復包絡可寫成

應用傅里葉變換對

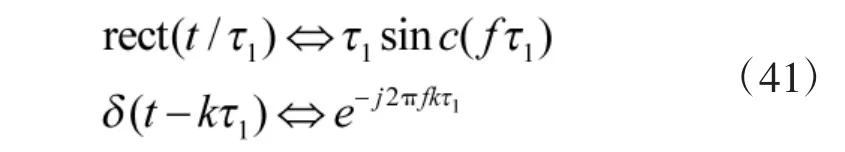
和傅里葉變換的性質，可得

由傅里葉變換的時域卷積定理，得偽隨機二相編碼信號的頻譜函數為

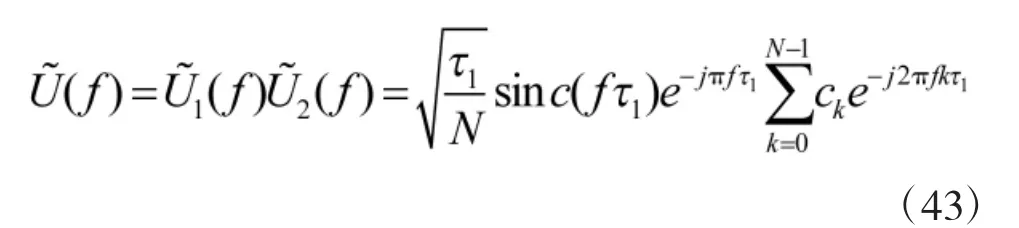
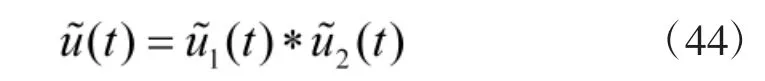
式中

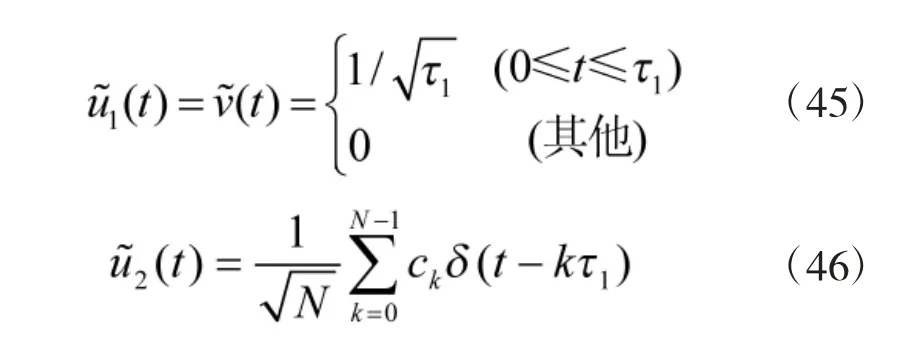
偽隨機二相編碼信號的模糊函數，就是它的復合自相關函數，根據定義為

利用線性卷積的運算性質，得偽隨機二相編碼信號的模糊函數為

2 仿真軟件的結構與功能

通用雷達信號仿真軟件可以簡便快速地獲得各種載波頻率，脈沖寬度等數據的單載頻矩形脈沖信號、線性調頻矩形脈沖信號和偽隨機二相編碼信號的數據、波形、頻譜，包括模糊函數。

從而，在學習的過程中，學員能夠直觀形象地學習和理解各種雷達脈沖信號，同時對于相關的科研工作，能夠提供所需的各種雷達信號數據，為雷達信號處理相關算法研究提供數據支撐。

為了實現上述功能，設計了通用脈沖雷達信號仿真軟件，如圖1 所示為設計仿真軟件的結構圖。

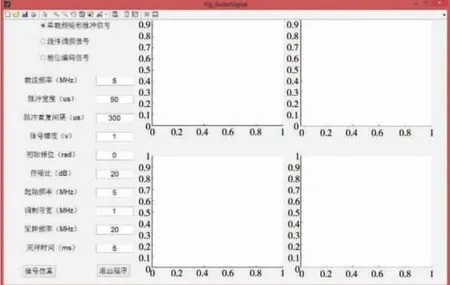
圖1 仿真軟件結構圖

其中，左上部分是3 種典型雷達信號的脈沖信號選擇，包含了單載頻矩形脈沖信號，線性調頻矩形脈沖信號以及偽隨機二相編碼信號。

左下是各種雷達信號參數的設置，包括載波頻率、脈沖寬度、脈沖重復間隔、信號幅度、初始相位、信噪比、起始頻率、調制帶寬、采樣頻率和采樣時間。

右側是仿真所得到的4 種結果圖，分別為信號幅度-采樣時間圖、信號幅度-采樣點數圖、信號頻譜圖以及模糊函數圖。通過此軟件即可實現對雷達信號的波形，復包絡，頻譜，以及模糊函數的提取。

參數設置如下：

載波頻率：3 MHz，脈沖寬度：75 us，脈沖重復間隔：300 us，信號幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始頻率：3 MHz，調制帶寬：1 MHz，采樣頻率：20 MHz，采樣時間：5 ms。

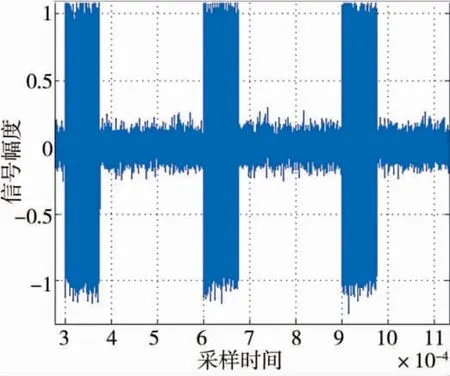
圖2 單載頻矩形脈沖信號時域描述圖

通過觀察圖2，可得到脈沖寬度為75 us，脈沖重復間隔為300 us，符合參數設置。

圖3 單載頻矩形脈沖信號單個脈沖圖

通過觀察圖3、下頁圖4，可得到載波頻率為3 MHz，調制帶寬為1 MHz，符合參數設置。

通過觀察圖5，可得到單載頻矩形脈沖信號的模糊函數圖為正刀刃型，符合該信號模糊函數的特點。

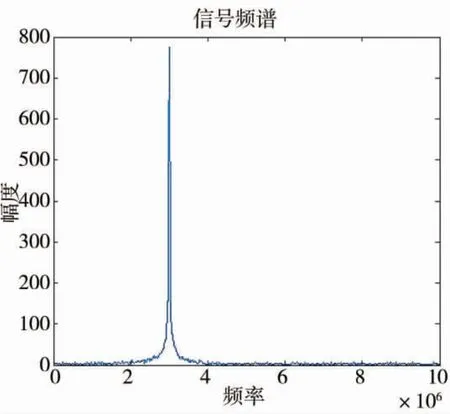
圖4 單載頻矩形脈沖信號頻譜圖

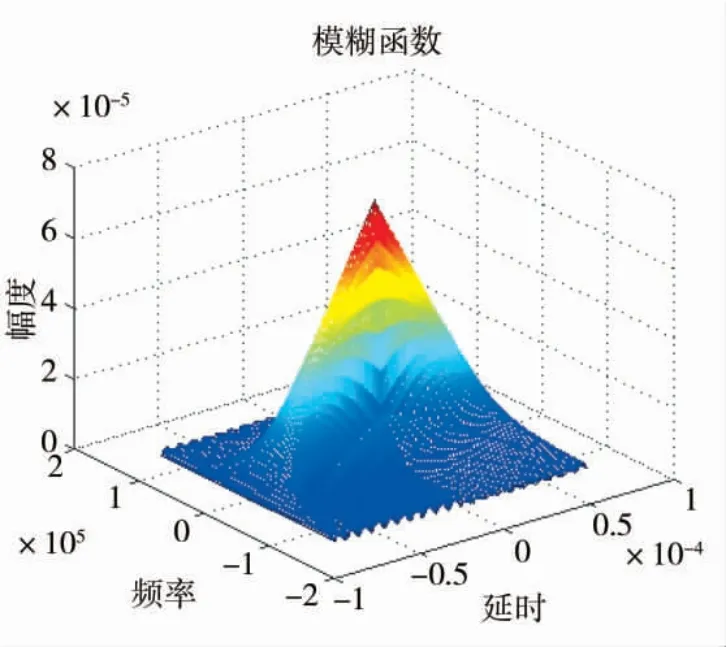
圖5 單載頻矩形脈沖信號模糊函數圖

參數設置如下：

載波頻率：10 MHz，脈沖寬度：25 us，脈沖重復間隔：200 us，信號幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始頻率：10 MHz，調制帶寬：1 MHz，采樣頻率：50 MHz，采樣時間：5 ms。

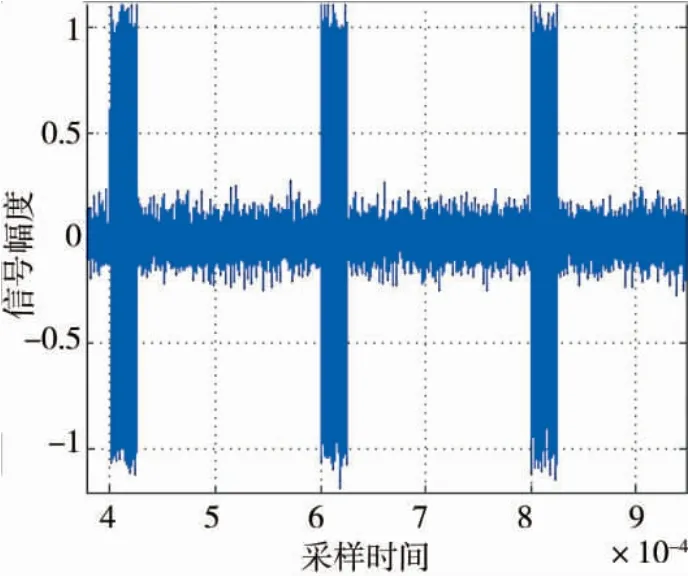
圖6 線性調頻矩形脈沖信號時域描述圖

通過觀察圖6，可得到脈沖寬度為25 us，脈沖重復間隔為200 us，符合參數設置。

通過觀察圖7、圖8，可得到載波頻率為10 MHz，調制帶寬為1 MHz，符合參數設置。

通過觀察圖9，可得到單載頻矩形脈沖信號的模糊函數圖為斜刀刃型，符合該信號模糊函數的特點。

參數設置如下：

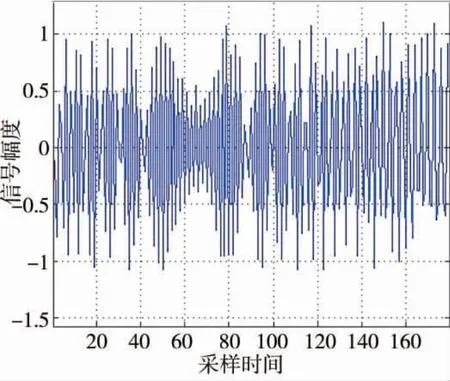
圖7 線性調頻矩形脈沖信號單個脈沖圖

圖8 線性調頻矩形脈沖信號頻譜

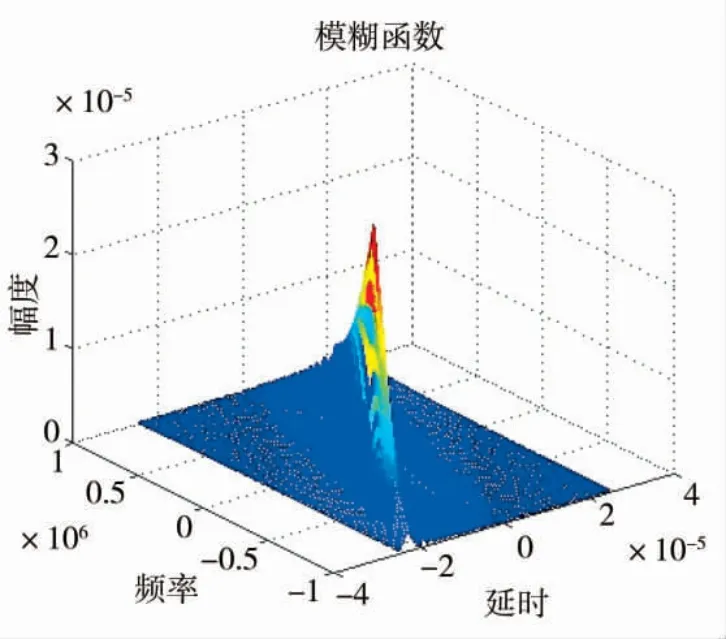
圖9 線性調頻矩形脈沖信號模糊函數圖

載波頻率：5 MHz，脈沖寬度：50 us，脈沖重復間隔：300 us，信號幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始頻率：5 MHz，調制帶寬：1 MHz，采樣頻率：20 MHz，采樣時間：5 ms。

通過觀察下頁圖10，可得到脈沖寬度為50 us，脈沖重復間隔為300 us，符合參數設置。

通過觀察圖11、圖12，可得到載波頻率為5 MHz，調制帶寬為1 MHz，符合參數設置。

通過觀察圖13，可得到單載頻矩形脈沖信號的模糊函數圖為釘型，符合該信號模糊函數的特點。

3 結論

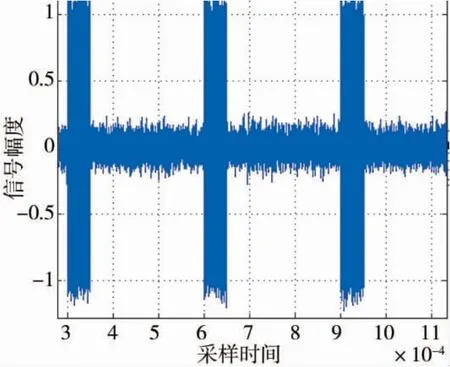
圖10 偽隨機二相編碼信號時域描述圖

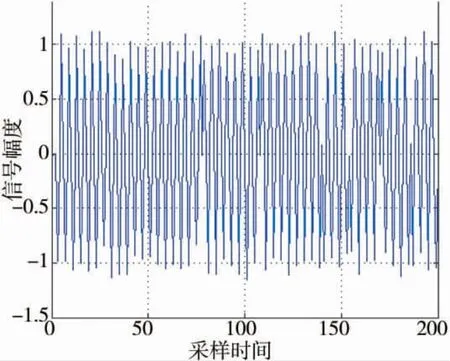
圖11 偽隨機二相編碼信號單個脈沖圖

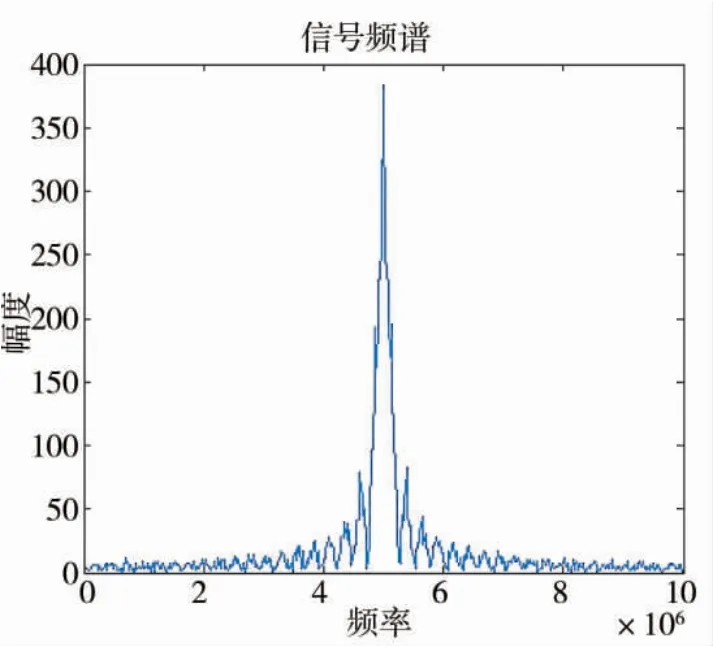
圖12 偽隨機二相編碼信號頻譜圖

圖13 偽隨機二相編碼信號模糊函數圖

本文以雷達信號的基本理論為引子，從雷達信號的時域表示、頻域表示以及模糊函數開始入手，閱讀搜集了大量雷達信號理論方面的資料，歸納總結了3 種典型的雷達脈沖信號的復包絡、時域描述、頻譜函數、模糊函數及其特點，以此為基礎建立了3 種雷達脈沖信號的完整的數學模型，最后，基于Matlab 仿真軟件對3 種典型的雷達脈沖信號進行了仿真實現，設計并編寫了通用雷達脈沖信號仿真軟件。通過對比試驗結果圖，發現與理論分析是一致的。

通用脈沖雷達信號仿真軟件的實現，不但解決了軍校學員在學習雷達理論時無法很好地理解相關知識的難題，還能夠為相關的科研工作提供所需的各種雷達信號數據，完成雷達信號處理相關算法研究。

但是，在本次研究設計中，僅僅完成了3 種典型雷達脈沖信號的仿真設計，在繁復的雷達種類中，要想更好地獲取相關實驗數據，如信號復包絡、模糊圖等，仍缺少相應的手段。因此，在下一步工作中，會針對其他的各種復雜雷達信號進行學習分析，并努力歸納整理出相關的理論，逐步地完成更加復雜的雷達信號的仿真設計與實現。