基于多源傳感器的單星定位算法與精度分析

鄧彥鑫，郭 偉，李柯陶

（中國(guó)航空無(wú)線(xiàn)電電子研究所，上海 200241）

0 引言

全球?qū)Ш叫l(wèi)星系統(tǒng)（Global Navigation Satellite Systems，GNSS）憑借其高精度、應(yīng)用便捷、覆蓋范圍廣且全天候全天時(shí)服務(wù)等諸多優(yōu)勢(shì)成為目前性?xún)r(jià)比最高、應(yīng)用領(lǐng)域最廣的定位導(dǎo)航授時(shí)系統(tǒng)［1］。但其存在一個(gè)重大的問(wèn)題，就是衛(wèi)星信號(hào)的羸弱性。衛(wèi)星信號(hào)從幾萬(wàn)公里的太空傳到地球表面，信號(hào)極易受到干擾，遮蔽和欺騙。當(dāng)衛(wèi)星信號(hào)由于受到建筑物，山體等遮擋而導(dǎo)致接收機(jī)接收到的衛(wèi)星空間分布不好甚至衛(wèi)星數(shù)少于4 顆時(shí)，衛(wèi)星導(dǎo)航接收機(jī)將無(wú)法提供實(shí)時(shí)定位。或在極端戰(zhàn)爭(zhēng)時(shí)期，GNSS 可被各式反衛(wèi)星技術(shù)輕易破壞或摧毀而失效，應(yīng)急響應(yīng)發(fā)射備用衛(wèi)星時(shí)，往往很難同時(shí)發(fā)射4 顆及以上數(shù)量的衛(wèi)星并完成快速組網(wǎng)提供服務(wù)。此外衛(wèi)星空間載荷異常、地面控制端出現(xiàn)故障等也可能造成GNSS 的定位，導(dǎo)航和授時(shí)（Positioning，Navigation and Timing，PNT）服務(wù)中斷。因此，實(shí)現(xiàn)可見(jiàn)衛(wèi)星數(shù)目不足時(shí)的應(yīng)急定位至關(guān)重要，國(guó)內(nèi)外的諸多學(xué)者針對(duì)該問(wèn)題，提出采用單星定位系統(tǒng)作為衛(wèi)星導(dǎo)航星座拒止服務(wù)環(huán)境下的應(yīng)急響應(yīng)系統(tǒng)，采用大橢圓軌道并在軌道遠(yuǎn)地點(diǎn)為用戶(hù)提供定位服務(wù)，以滿(mǎn)足長(zhǎng)時(shí)間服務(wù)的要求，而在近地點(diǎn)衛(wèi)星會(huì)快速通過(guò)非服務(wù)區(qū)［2］。對(duì)國(guó)內(nèi)外近些年已公開(kāi)的文獻(xiàn)分析可知，這種定位方法衛(wèi)星的定軌精度較低，所以定位誤差較大，僅憑單顆衛(wèi)星的測(cè)量信息是無(wú)法完成高精度的定位功能，其定位精度總會(huì)受到相關(guān)因素的制約［3-8］。因此，需要考慮加入高精度外部傳感器的方式輔助定位。

本文在假設(shè)接收機(jī)只獲得一顆衛(wèi)星信號(hào)的極端條件下，分析利用多源傳感器信息輔助單星定位的可行性，提出了基于多源傳感器信息的單星定位算法。通過(guò)添加高精度氣壓高度計(jì)提供系統(tǒng)高度信息以及芯片級(jí)原子鐘（Chip Scale Atomic Clock，CSAC）消除接收機(jī)時(shí)鐘鐘差的方法，增加衛(wèi)星定位測(cè)距算法中的輔助方程，從而實(shí)現(xiàn)使用更少時(shí)刻的衛(wèi)星數(shù)據(jù)提供定位服務(wù)，最終解決單星定位過(guò)程中由于衛(wèi)星空間分布差造成定位精度低的問(wèn)題。通過(guò)理論分析、數(shù)字仿真實(shí)驗(yàn)和靜態(tài)試驗(yàn)的方法，對(duì)提出的算法精度和有效性進(jìn)行了分析和驗(yàn)證。

1 定位方法

1.1 定位原理

多源傳感器信息輔助下的單星連續(xù)測(cè)距定位原理如圖1 所示。即假設(shè)用戶(hù)靜止不動(dòng)，接收機(jī)持續(xù)觀測(cè)收集不同時(shí)刻t 衛(wèi)星的偽距測(cè)量值，以及各項(xiàng)偏差、誤差成分的校正量（衛(wèi)星部分誤差校正量）、I（t電離層延時(shí)校正量）、T（t對(duì)流層延時(shí)校正量）和（多路徑誤差校正量）等，從而獲得各時(shí)刻校正后的衛(wèi)星偽距觀測(cè)值，以及各時(shí)刻由衛(wèi)星星歷計(jì)算并經(jīng)地球自轉(zhuǎn)校正后的衛(wèi)星位置坐標(biāo)。

由于利用CSAC 代替TCXO 作為接收機(jī)內(nèi)部時(shí)鐘，可認(rèn)為由接收機(jī)時(shí)鐘誤差造成的偽距測(cè)量誤差（厘米級(jí)）可忽略不計(jì)。

圖1 單星連續(xù)測(cè)距定位原理圖

假設(shè)未知用戶(hù)的位置坐標(biāo)為（x，y，z），根據(jù)t1、t2到tn這n 個(gè)時(shí)刻的偽距測(cè)量值可建立如下非線(xiàn)性方程組：

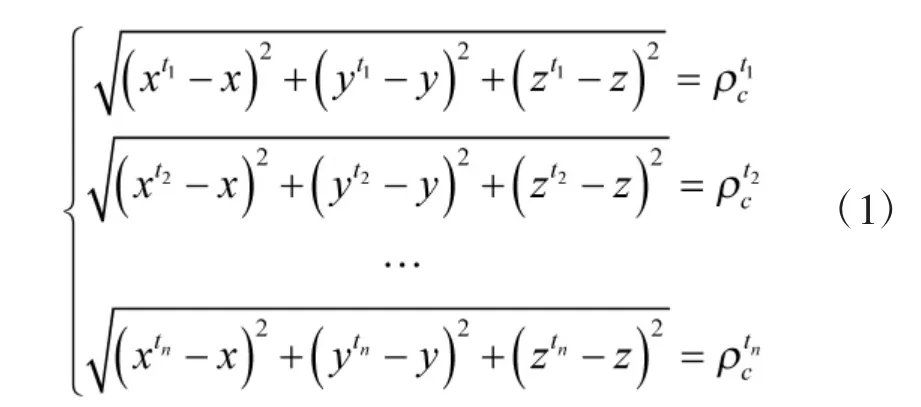
在接收機(jī)的三維位置坐標(biāo)經(jīng)度、緯度和高度中，通常高度信息可通過(guò)外部輔助設(shè)備（如氣壓高度計(jì)、電子地圖等）測(cè)定，或在一個(gè)區(qū)域內(nèi)可認(rèn)為高度值固定已知，此時(shí)只需求解接收機(jī)在水平方向上的二維位置坐標(biāo)分量，便可精確獲得接收機(jī)的位置。同時(shí)減少未知數(shù)的求解可增加定位時(shí)的信息冗余度，從而提高接收機(jī)在水平方向的定位精度。

具體到方程組的求解時(shí)，雖然已知用戶(hù)的高度值，但該高度是指地球坐標(biāo)系g系中運(yùn)載體的高度h，而在地心地固坐標(biāo)系e 系中運(yùn)載體的三維坐標(biāo)（x，y，z）仍均為未知數(shù)，因此，不能通過(guò)直接減少一個(gè)未知數(shù)來(lái)完成定位求解，而是增加輔助方程個(gè)數(shù)，即建立高度與運(yùn)載體三維坐標(biāo)間的關(guān)系式并添加到定位方程組中使得系統(tǒng)只需觀測(cè)兩個(gè)時(shí)刻的衛(wèi)星數(shù)據(jù)便可完成定位解算。

用戶(hù)高度h 與其三維位置坐標(biāo)（x，y，z）之間的關(guān)系式如下：其中，Re、Rp和RN分別為地球的長(zhǎng)半軸、短半軸和運(yùn)載體所在地的卯酉圈曲率半徑。簡(jiǎn)化計(jì)算可得用戶(hù)的高度曲面方程

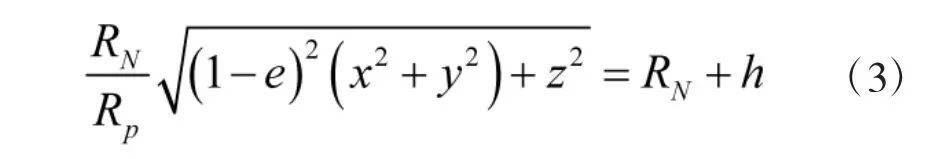
其中，e 為地球偏心率。

與傳統(tǒng)定位方法相比，單星連續(xù)測(cè)距定位采用“以時(shí)間換空間”的原理，利用衛(wèi)星隨時(shí)間在空間幾何位置的變化彌補(bǔ)了系統(tǒng)的可觀測(cè)性，為系統(tǒng)提供了足夠的量測(cè)信息用于求解方程組，采樣時(shí)間間隔越長(zhǎng)，衛(wèi)星不同時(shí)刻間的位置幾何分布越好，定位精度越高。同時(shí)該方法利用了CSAC 的高精度授時(shí)功能，降低了定位時(shí)的測(cè)量維度，提高了系統(tǒng)的性能。

將式（3）加入到式（1）中組成基于多源傳感器信息的單星定位方程組，采用最小二乘法進(jìn)行求解，具體解算過(guò)程因篇幅原因不做贅述，可參考文獻(xiàn)［10-11］。

1.2 精度分析

考慮接收機(jī)觀測(cè)衛(wèi)星并獲得偽距過(guò)程中tn時(shí)刻的偽距測(cè)量誤差，則由最小二乘法解得線(xiàn)性化矩陣

其中

式（6）表明了偽距測(cè)量誤差與定位誤差之間的關(guān)系，一般以均值和方差來(lái)描述測(cè)量誤差對(duì)定位誤差的影響大小，從簡(jiǎn)化定位精度理論分析考慮，我們做以下兩點(diǎn)假設(shè)分別闡述。

則測(cè)量誤差向量ε 的均值為

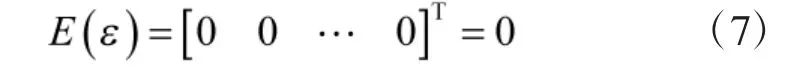
假設(shè)各時(shí)刻衛(wèi)星測(cè)量之中偽距測(cè)量誤差的各部分誤差相互獨(dú)立，則有

其中，σS代表由衛(wèi)星時(shí)鐘誤差和衛(wèi)星星歷誤差造成的偽距測(cè)量誤差標(biāo)準(zhǔn)差，值約為3 m，σP代表衛(wèi)星信號(hào)傳播中電離層延時(shí)和對(duì)流層延時(shí)造成的偽距測(cè)量誤差標(biāo)準(zhǔn)差，值約為5 m，σR代表與接收機(jī)和多路徑有關(guān)的誤差造成的偽距測(cè)量誤差標(biāo)準(zhǔn)差，值約為1 m。計(jì)算可得偽距測(cè)量誤差造成的定位誤差約為5.9 m。實(shí)際中的估算方法要更復(fù)雜，包括考慮衛(wèi)星信號(hào)強(qiáng)度，衛(wèi)星仰角值和接收機(jī)跟蹤環(huán)路運(yùn)行狀態(tài)等具體指標(biāo)，這里不做深入探討。

2）假設(shè)衛(wèi)星各時(shí)刻間的測(cè)量誤差不相關(guān)。

此時(shí)測(cè)量誤差向量ε 的協(xié)方差矩陣Kε為

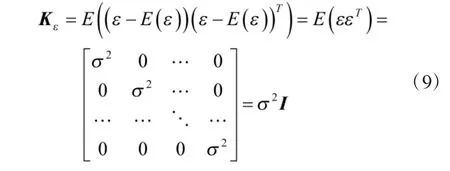
其中，I 為n×n 的單位陣。實(shí)際測(cè)量時(shí)，由于是接收同一顆衛(wèi)星的發(fā)射信號(hào)，不同時(shí)刻間的測(cè)量誤差間肯定存在相關(guān)性，此處假設(shè)只是為簡(jiǎn)化定位誤差協(xié)方差矩陣的推導(dǎo)。則由式（6）和式（9）可得

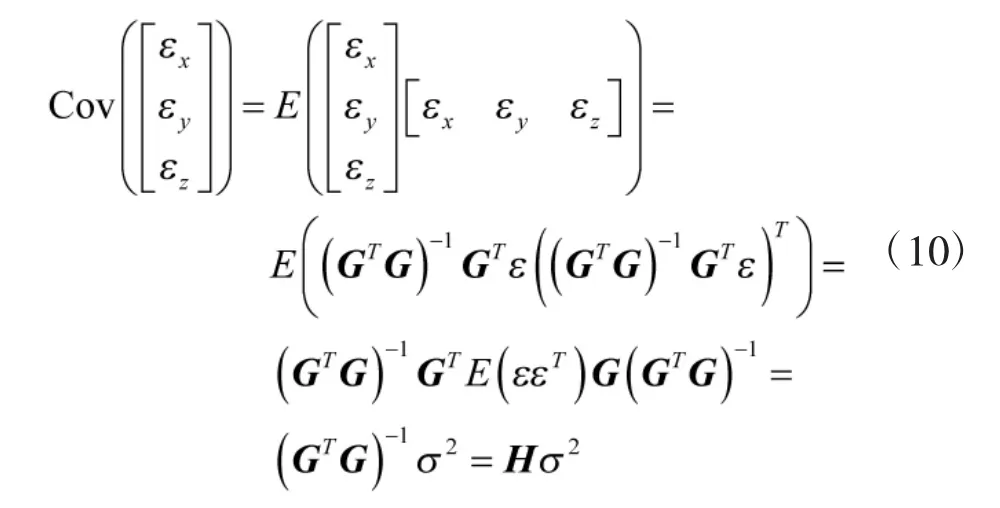
采用幾何精度因子GDOP 來(lái)表示誤差的放大倍數(shù)，其計(jì)算方法為

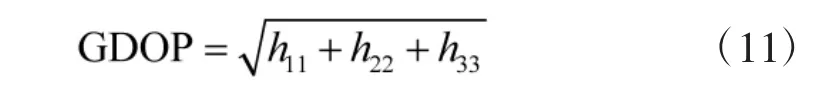
將定位誤差從地心地固坐標(biāo)系轉(zhuǎn)化到地理坐標(biāo)系中有

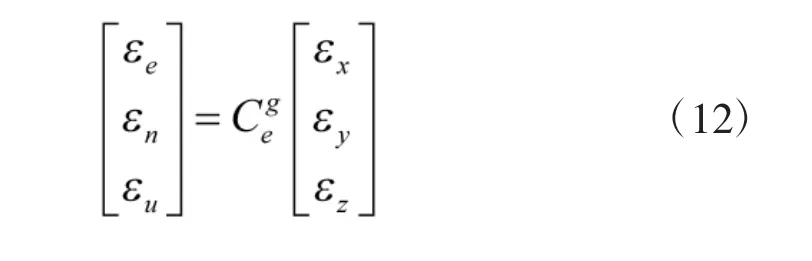
其中

為地心地固坐標(biāo)系到地球坐標(biāo)系的方向余弦矩陣。

則式（10）在地球坐標(biāo)系下的表示為

GDOP 值越小，定位誤差越小。

將式（4）不考慮偽距測(cè)量誤差投影到地球坐標(biāo)系中有

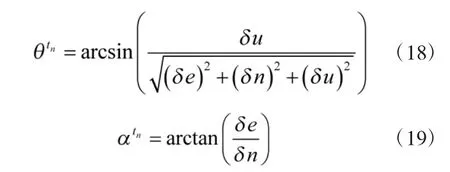
2 驗(yàn)證分析

為了驗(yàn)證所設(shè)計(jì)的基于多源傳感器的單星定位算法的有效性和精度，本文采用數(shù)字仿真驗(yàn)證和跑車(chē)動(dòng)態(tài)試驗(yàn)方式進(jìn)行驗(yàn)證。1）數(shù)字仿真驗(yàn)證：通過(guò)仿真衛(wèi)星的軌道實(shí)現(xiàn)衛(wèi)星的仿真數(shù)據(jù)激勵(lì)，模擬靜態(tài)載體長(zhǎng)時(shí)間只接收一顆衛(wèi)星的星歷數(shù)據(jù)，對(duì)不同數(shù)量傳感器輔助下的單星定位算法進(jìn)行了有效性仿真驗(yàn)證，采用蒙特卡洛分析法對(duì)算法的定位精度數(shù)據(jù)進(jìn)行了統(tǒng)計(jì)分析；2）靜態(tài)試驗(yàn)驗(yàn)證：利用GNSS 單頻接收機(jī)、高精度氣壓高度計(jì)和CSAC 搭建基于C 多傳感器的單星定位靜態(tài)試驗(yàn)環(huán)境，完成對(duì)一顆衛(wèi)星信號(hào)的持續(xù)觀測(cè)，并利用所獲得的試驗(yàn)數(shù)據(jù)對(duì)單星定位系統(tǒng)進(jìn)行了精度評(píng)估，最終驗(yàn)證基于多源傳感器信息的單星定位算法在實(shí)際應(yīng)用時(shí)的有效性和精度。

2.1 數(shù)字仿真驗(yàn)證

利用自行設(shè)計(jì)的理想圓軌道衛(wèi)星仿真軟件，載入一顆編號(hào)為“4”的在軌衛(wèi)星進(jìn)行仿真數(shù)據(jù)激勵(lì)，其衛(wèi)星軌道特征如表1 所示。

選擇衛(wèi)星的過(guò)頂時(shí)間作為單星定位服務(wù)時(shí)間段，其運(yùn)行時(shí)長(zhǎng)為1 h，用戶(hù)位置為（北緯34.25°，東經(jīng)108.91°，高380 m），星下點(diǎn)軌跡如圖2 所示。

由于短時(shí)間內(nèi)衛(wèi)星運(yùn)行距離較短，導(dǎo)致不同時(shí)刻的衛(wèi)星依然集中在一起或在一條直線(xiàn)上，這時(shí)不同時(shí)刻衛(wèi)星的幾何分布很差，因此，本試驗(yàn)選取t=300 s 時(shí)刻為起始解算時(shí)刻，即單星定位接收機(jī)開(kāi)機(jī)前5 min 只做數(shù)據(jù)收集工作，從5 min 開(kāi)始做定位解算，每個(gè)時(shí)刻t 選取3 個(gè)時(shí)刻的衛(wèi)星信息作為偽距量測(cè)信息，這3 個(gè)時(shí)刻分別為1、t/2 和t 時(shí)刻，以確保衛(wèi)星的幾何分布結(jié)果最好。

表1 “4”號(hào)衛(wèi)星軌道特征表

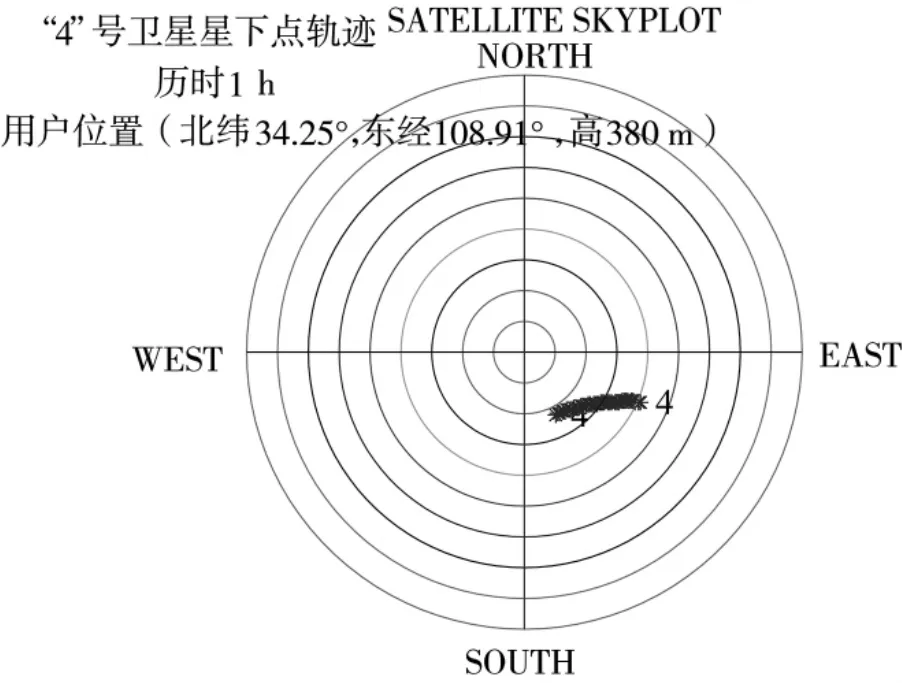
圖2 “4”號(hào)衛(wèi)星1 h 運(yùn)行星下點(diǎn)軌跡圖

分別選擇注入偽距觀測(cè)誤差均方差為1 m 和3 m，在上述仿真環(huán)境下進(jìn)行單星定位解算，根據(jù)上述仿真條件，其中當(dāng)偽距觀測(cè)誤差均方差為1 m 時(shí)，得到用戶(hù)的三維定位結(jié)果誤差和幾何精度因子GDOP 隨時(shí)間的變化如圖3、圖4 所示（程序橫坐標(biāo)軸t 時(shí)刻為接收機(jī)開(kāi)機(jī)后（t+300）s 時(shí)刻）。

圖3 偽距測(cè)量誤差為1 m 時(shí)的單星定位結(jié)果

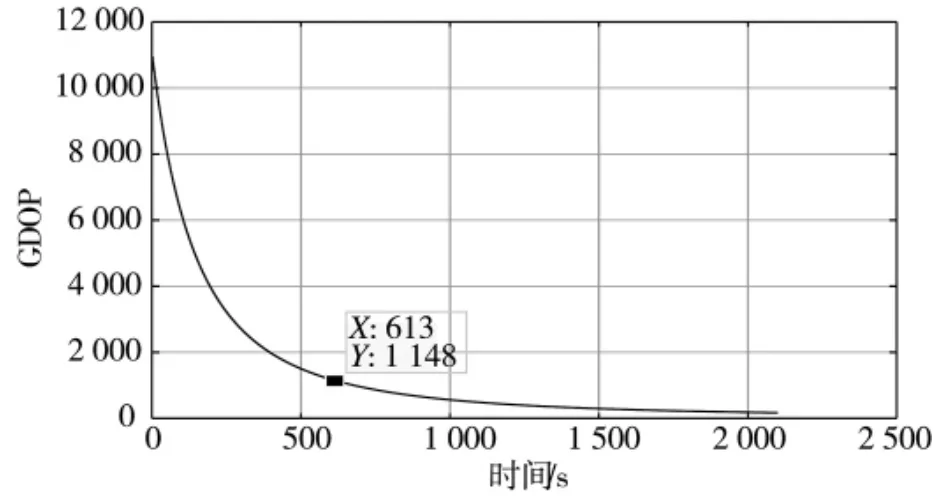
圖4 偽距測(cè)量誤差為1 m 時(shí)的GDOP

由圖3 可知，當(dāng)偽距測(cè)量誤差均方差為1 m 時(shí)，僅以CSAC 輔助單星定位解算是可行的，仿真在900 s 左右完成了精度為1 km 的定位。由圖4 可知，隨著時(shí)間的增加，系統(tǒng)的GDOP 值在減小，即所選取3 個(gè)時(shí)刻的衛(wèi)星的幾何分布越來(lái)越好，但在900 s左右時(shí)GDOP 值仍在103的數(shù)量級(jí)別，這表明單星定位短期效果仍遠(yuǎn)差于傳統(tǒng)的多星定位。

利用蒙特卡洛仿真分析單星定位精度的統(tǒng)計(jì)特性，分別對(duì)用戶(hù)偽距測(cè)量誤差均方差為1 m 和3 m，采樣時(shí)間為600 s 和1 200 s 時(shí)的單星定位進(jìn)行100 次蒙特卡洛仿真，求得其結(jié)果的RMS 誤差作為單星定位統(tǒng)計(jì)精度，其中偽距誤差為1 m，采樣時(shí)間為1 200 s 時(shí)的蒙特卡洛仿真統(tǒng)計(jì)結(jié)果如圖5 所示，總的仿真統(tǒng)計(jì)結(jié)果如表2 所示。

由表2 結(jié)果可知，基于CSAC 輔助的靜態(tài)單星定位雖然可行，但由于僅能利用1 顆衛(wèi)星的數(shù)據(jù)，多個(gè)時(shí)刻衛(wèi)星的空間幾何分布很差，導(dǎo)致GDOP 過(guò)大，當(dāng)偽距測(cè)量誤差的均方差為1 m 時(shí)，需持續(xù)觀測(cè)20 min 方能達(dá)到400 m 的定位精度，而當(dāng)偽距測(cè)量誤差的均方差只增加2 m（從1 m 到3 m）時(shí)，最終定位精度便從365.926 m 上升到1 270.489 m，可見(jiàn)單星定位系統(tǒng)是及其脆弱的，即使利用CSAC 降低了一維的測(cè)量維度信息，最終定位結(jié)果仍隨較小的偽距測(cè)量誤差的變化發(fā)生較大的波動(dòng)，其根本原因就是短時(shí)間測(cè)量得到的3 個(gè)時(shí)刻的3 個(gè)衛(wèi)星位置之間的空間相關(guān)性很高，衛(wèi)星的幾何分布很差，從而使得權(quán)系矩陣H（或）的元素值過(guò)大。

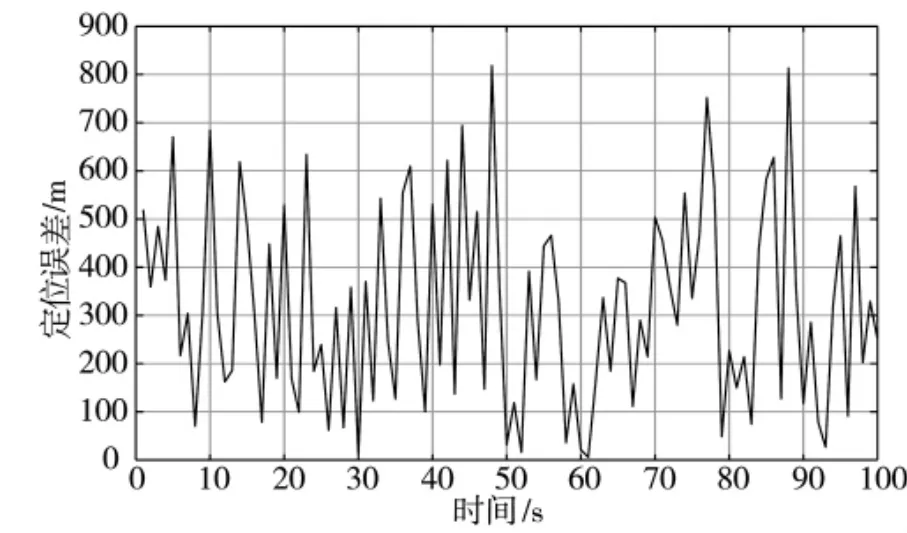
圖5 偽距測(cè)量誤差為1 m 時(shí)的100 次蒙特卡洛仿真統(tǒng)計(jì)

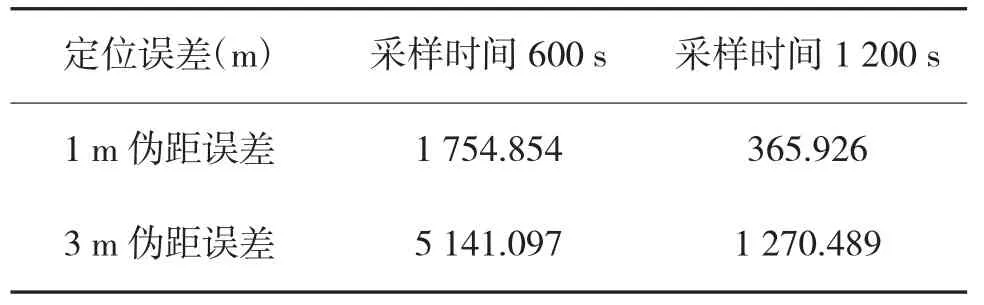
表2 基于CSAC 的單星連續(xù)測(cè)距定位精度（RMS）

設(shè)置仿真條件同上，并只采用兩個(gè)時(shí)刻（1 時(shí)刻與t 時(shí)刻）的衛(wèi)星數(shù)據(jù)，假設(shè)用戶(hù)高度信息h=380 m可通過(guò)外部輔助器件測(cè)量獲得。考慮實(shí)際測(cè)量時(shí)仍會(huì)代入一定的測(cè)量誤差，設(shè)置注入誤差：偽距測(cè)量誤差均方差1 m，高度測(cè)量誤差均方差3 m。仿真可得基于高度信息與時(shí)鐘誤差約束下的單星定位誤差結(jié)果如圖6 所示。

圖6 基于高度信息與時(shí)鐘誤差約束下的單星定位

由圖6 可知，基于高度信息與時(shí)鐘誤差約束下的單星系統(tǒng)在約100 s 便完成了1 km 精度的定位，所用時(shí)間遠(yuǎn)小于僅用CSAC 輔助的單星定位系統(tǒng)（約900 s），同時(shí)經(jīng)100 次蒙特卡洛仿真統(tǒng)計(jì)可知系統(tǒng)可在200 s 完成327.25 m（RMS）的定位精度，在300 s 完成240.56 m（RMS）的定位精度，系統(tǒng)的整體性能均遠(yuǎn)優(yōu)于僅利用CSAC 輔助的單星定位系統(tǒng)。仿真可得當(dāng)偽距測(cè)量誤差為1 m，連續(xù)觀測(cè)200 s 時(shí)高度測(cè)量誤差對(duì)系統(tǒng)定位精度（RMS）的影響如圖7所示。

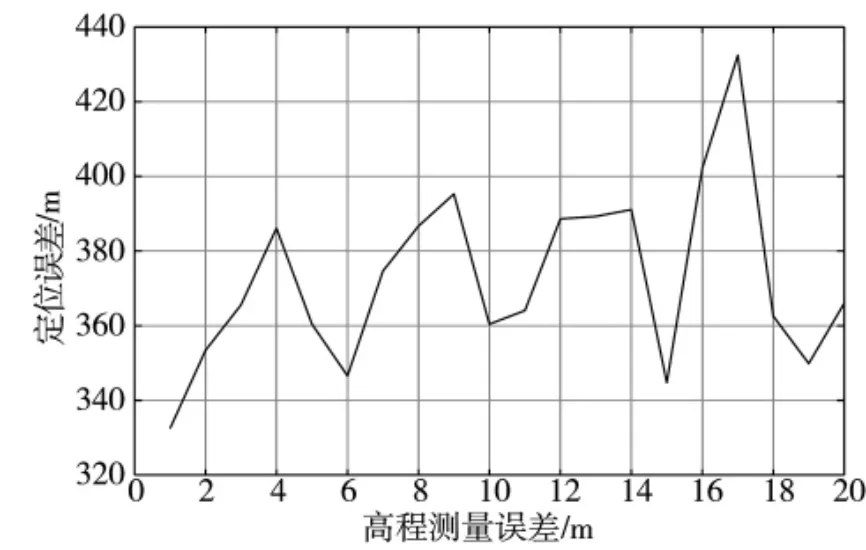
圖7 高度測(cè)量誤差對(duì)系統(tǒng)定位精度（RMS）的影響

由圖7 可知與偽距測(cè)量誤差相比，高程測(cè)量誤差并不是造成高度信息約束下單星定位誤差的主要誤差源。由于該方法滿(mǎn)足在緊急情況下僅利用單星測(cè)量數(shù)據(jù)定位的精度指標(biāo)（定位時(shí)間<5 min，定位精度500 m），因此，可廣泛應(yīng)用于應(yīng)急定位服務(wù)中。

2.2 靜態(tài)試驗(yàn)驗(yàn)證

由于基于多源傳感器信息的單星連續(xù)測(cè)距定位算法需求接收機(jī)對(duì)衛(wèi)星連續(xù)觀測(cè)一段時(shí)間方能定位，因此，該方法并不適用于載體動(dòng)態(tài)環(huán)境下的實(shí)時(shí)定位，在利用實(shí)際數(shù)據(jù)對(duì)該算法做試驗(yàn)驗(yàn)證時(shí)也只能采用靜態(tài)試驗(yàn)數(shù)據(jù)。本節(jié)利用GNSS 單頻接收機(jī)、高精度氣壓高度計(jì)和CSAC，搭建基于多源傳感器信息的單星定位靜態(tài)試驗(yàn)環(huán)境，在衛(wèi)星信號(hào)拒止環(huán)境下完成對(duì)一顆衛(wèi)星信號(hào)的持續(xù)觀測(cè)，并利用所獲得的試驗(yàn)數(shù)據(jù)對(duì)單星定位系統(tǒng)進(jìn)行了精度評(píng)估，最終驗(yàn)證基于多源傳感器信息的單星連續(xù)測(cè)距定位算法在實(shí)際應(yīng)用時(shí)的有效性。

2.2.1 驗(yàn)證環(huán)境

為驗(yàn)證所設(shè)計(jì)的單星連續(xù)測(cè)距定位算法的實(shí)用性，在實(shí)驗(yàn)室搭建靜態(tài)試驗(yàn)數(shù)據(jù)采集和算法仿真驗(yàn)證環(huán)境如圖8 所示。實(shí)驗(yàn)環(huán)境主要由Microsemi公司生產(chǎn)的型號(hào)為SA.45s 的CSAC、1 臺(tái)Novatel OEM 638 高精度GNSS 接收機(jī)、臺(tái)式計(jì)算機(jī)、1 根GNSS 天線(xiàn)、RAS-2 型氣壓高度計(jì)以及若干導(dǎo)線(xiàn)組成。

在實(shí)現(xiàn)單星靜態(tài)定位試驗(yàn)數(shù)據(jù)采集與處理前，先進(jìn)行兩個(gè)預(yù)試驗(yàn)，分別為接收機(jī)高度測(cè)定試驗(yàn)和CSAC 馴服試驗(yàn)。其中接收機(jī)高度測(cè)定試驗(yàn)為靜態(tài)試驗(yàn)提供接收機(jī)高精度高度先驗(yàn)信息，CSAC 馴服試驗(yàn)完成CSAC 對(duì)接收機(jī)內(nèi)時(shí)鐘的替代，從而為主試驗(yàn)的順利完成奠定了基礎(chǔ)，由于篇幅原因，本文對(duì)這兩個(gè)預(yù)實(shí)驗(yàn)不做贅述。

2.2.2 定位數(shù)據(jù)分析

圖8 單星定位靜態(tài)試驗(yàn)環(huán)境

設(shè)置觀測(cè)時(shí)間為2019 年9 月29 日22：10 到2019 年9 月29 日22：20。GNSS 接收機(jī)天線(xiàn)在該時(shí)間內(nèi)只能接收PRN 編號(hào)為“5”的衛(wèi)星數(shù)據(jù)，SA.45 s負(fù)責(zé)提供這一時(shí)段的時(shí)鐘基準(zhǔn)，先驗(yàn)高度信息為410.5 m。將接收機(jī)在0.5 h 內(nèi)對(duì)“5”號(hào)衛(wèi)星持續(xù)觀測(cè)并記錄的衛(wèi)星星歷數(shù)據(jù)和原始觀測(cè)信息輸入到計(jì)算機(jī)中分析處理，得到10 min 內(nèi)衛(wèi)星的實(shí)時(shí)位置與偽距測(cè)量值，利用高度信息和時(shí)鐘誤差約束下的單星定位算法，對(duì)這組數(shù)據(jù)進(jìn)行定位解算并與接收機(jī)實(shí)際位置比較可得算法的定位精度，所得結(jié)果如圖9 所示。

試驗(yàn)結(jié)果可知，真實(shí)接收機(jī)經(jīng)過(guò)對(duì)一顆衛(wèi)星的連續(xù)觀測(cè)，輔以高精度CSAC 和氣壓高度計(jì)提供時(shí)鐘和高度信息，可在2 min 內(nèi)完成500 m 精度定位以及在5 min 內(nèi)完成200 m 精度定位，完全符合戰(zhàn)時(shí)應(yīng)急定位精度需求。但由于CSAC 只能消除接收機(jī)時(shí)鐘誤差和鐘漂，無(wú)法消除多路徑效應(yīng)、電磁干擾和接收機(jī)噪聲等其他誤差對(duì)偽距測(cè)量誤差的影響，接收機(jī)內(nèi)部模型也無(wú)法做到完整補(bǔ)償，因此，仍有小部分噪聲的存在引起定位結(jié)果收斂后的瞬時(shí)跳動(dòng)。

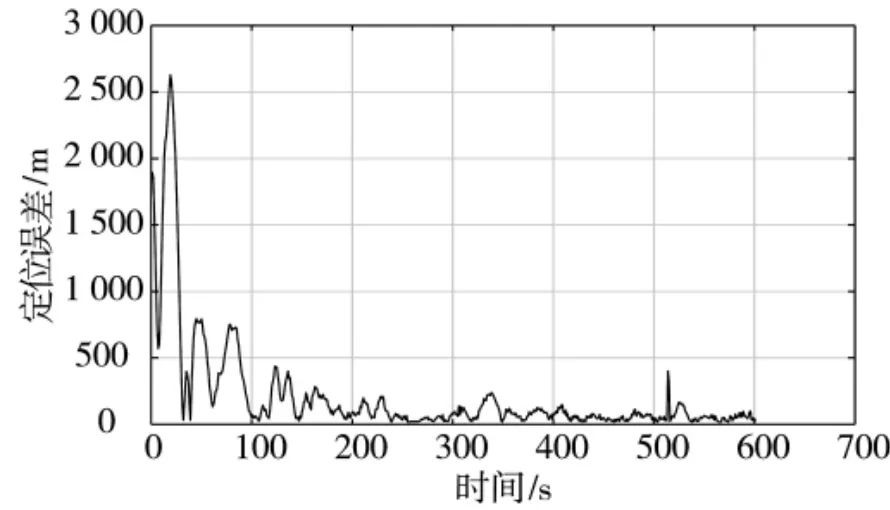
圖9 單星靜態(tài)三維定位精度

3 結(jié)論

本文在假設(shè)接收機(jī)只獲得一顆衛(wèi)星信號(hào)的極端條件下，對(duì)基于多源傳感器信息的單星連續(xù)測(cè)距定位算法及其精度分析作了理論分析探討，在此基礎(chǔ)上利用Matlab 軟件對(duì)上述算法進(jìn)行了仿真驗(yàn)證，最后搭建靜態(tài)試驗(yàn)平臺(tái)完成了C 多源傳感器信息輔助單星定位算法的靜態(tài)數(shù)據(jù)驗(yàn)證。仿真與實(shí)驗(yàn)結(jié)果表明，真實(shí)接收機(jī)經(jīng)過(guò)對(duì)一顆衛(wèi)星的連續(xù)觀測(cè)，輔以高精度CSAC 和氣壓高度計(jì)提供時(shí)鐘和高度信息，可在2 min 內(nèi)完成百米級(jí)精度定位，完全符合戰(zhàn)時(shí)應(yīng)急定位精度需求。