化歸思想在高中數學解題過程中的應用方法分析

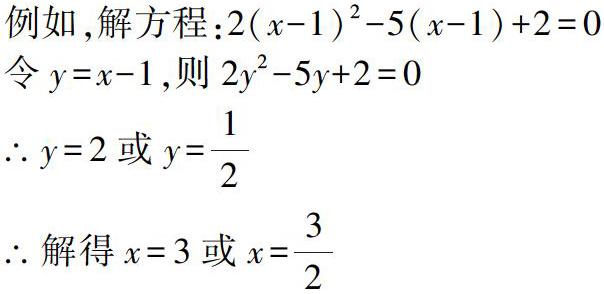
摘 要：隨著新課改的教學觀念深入，“關注學生發展、強調教師成長、重視以學定教”等理念逐漸深入課堂。高中的教學也著重于解題能力方面的培養，并將化歸思想作為日常解題過程中的新理念。在高中解題過程中，化歸思想是一個很重要的理念，通俗地講，就是將復雜問題簡單化。數學解題中，其實就是一個由難到易、由繁到簡的過程。作為學生，在解題過程中，要學會合理運用化歸思想，嘗試把陌生的知識點轉化為已經熟知的知識點，進而解決數學中的疑難問題。一言以蔽之，化歸思想是貫穿高中數學解題的一種重要思想，如果能夠熟練掌握化歸思想，并將其引入到解題過程中，那么困難的題目自然迎刃而解。

關鍵詞：化歸思想;數學解題;學會應用

在高中數學中，其實內容并不是很難，大多數課本中的知識內容都能夠理解，然而最難的是如何將學到的知識運用到日常的解題過程中，如何看到題目能夠準確定位這道題所考察的知識點，這是我們摸不到頭緒的難點問題。因為高中數學的知識比較零散，知識網比較復雜，如果想將所有的數學知識融會貫通，就要具備極強的抽象知識理解能力和邏輯思維能力，然而在絕大多數高中生中，都很難具備這兩種能力，最后就可能導致學生不能完全自主地去解決一些疑難問題，這也是高中數學成績整體并不是很理想的原因。然而將化歸思想滲透到高中數學疑難問題解決中，可以使得解題效率提高，能夠幫助解決一些沒見過的數學難題。化歸思想另一層含義就是化零散為統一，運用化歸思想，將疑難問題中的零散知識串聯在一起，使其成為統一的整體，這能夠有效地提高數學成績。

一、 化歸思想在高中數學解題過程中的具體應用

（一）化歸思想在高中函數問題中的應用分析

在高中數學的學習中，函數在整個高中數學中占很大部分比例，而且有的函數問題還極其刁鉆，讓人摸不著頭腦，可以說函數問題在整個高中都是疑難問題，并且分值很重。所以說，如果要將化歸思想引入到數學解題過程中來，應該著重注意將化歸思想與函數問題結合，并學會運用化歸思想來解決高中函數問題中的疑難知識點。教師著重注意將化歸思想與函數的教學相結合，在日常的教學中，要能夠熟練地掌握化歸思想解決函數問題，合理運用，學會變通，能夠靈活地使用此方法解決問題，總結類似問題，將各種問題具體分類。函數問題大概就是代表兩個量之間的關系，并結合數學公式將這兩個變量之間的關系動態的表達出來，在問題本身融入化歸思想，將日常生活中零散的知識串聯起來，各個知識點形成聯系，形成知識網，這樣就能又快又準地解決問題。

在絕大多數函數題目的解題過程中，經常會遇到一些未知問題，這些未知問題，如果不能及時轉變數學思維運用化歸思想來考慮問題，那么大多數情況需要一步一步來思考并尋找解決辦法的。對于函數中的未知問題，絕大多數情況都是可以轉變成已知的。所謂的未知轉化為已知，通俗來說就是將未知條件、未知理論轉化為已知的條件、理論，將未知與已知建立聯系，從而找到解決問題的方法。在三角函數的相關問題中，常常使用這種未知轉化為已知的方法去解決問題。在處理高中函數的疑難題中，也會經常引用化歸思想中的向題根轉化的方法，這是化歸思想的重要思維方式。所謂的題根就是這道題目所涉及的知識點，在高中數學的教學過程中，教師常常用題海戰術來提高成績，在這其中，學生會接觸大量的習題，大量的習題中的函數問題，其中會有大量信息需要去捕捉，這些信息往往讓人摸不到頭緒，但是將向題根轉化的思路貫穿整個解題過程中就會發現，這些沒見過的題目和課本中熟悉的內容有很大的聯系。很多問題雖然題目不同，但是它們的題根是大體相同的，在解題過程中需要用到的知識點是相同的，這樣就可以總結出題目相似的題型，總結出的題型就可以運用類似的解題過程來解題。

就此可以得出結論，如果遇到一些令人摸不到頭緒的題目，就可以利用向題根轉化的方法來解決問題。高中階段所學過的函數，無非就是幾個固定的模型，比如三角函數、冪函數、指數函數等等，這也就意味著，所有高中函數解題思路中，無非是向這幾個基本模型上面想，如果能熟練掌握這一思想，把所有未知題目都轉變為見過的或是熟悉的題目，這樣就能輕而易舉地把題目解出來。向題根轉化的方法是化歸思想中重要的方法之一，夠熟練掌握這一方法，逐步將化歸思想滲透自己的腦海里，遇到疑難問題學會運用此方法解決，如果能掌握化歸思想其中的規律，那么就可以更快很準確地解題。

本題為關于x-1的一元二次方程，如果將括號展開再化簡求解就會非常復雜，根據觀察，方程中都含有（x-1）的未知項，所以可以將它看做一個整體未知數，然后用換元法求解，這就是把復雜的問題簡單化，常規化歸思想的應用。

（二）化歸思想在高中數學立體幾何問題中的應用分析

在高中數學內容中，立體幾何往往是屬于重點難點問題，而且在高考中也占了很大的題型比例，不僅是在后邊的大題，在前面的選擇填空題都會有所涉及。所以說在高三的數學復習過程中，教師要學會引導學生參考大量的高考例題來深化學生在解題過程中運用化歸思想，使學生能夠充分理解。在立體幾何一些難點問題上，教師引導學生聯想課本中的概念，如果說能夠充分理解，那么再難的問題也會變的不堪一擊。之所以說高中立體幾何一直是重點、難點，這是因為立體幾何問題復雜多變。參考歷年來高考數學的立體幾何問題，可謂萬變不離其宗，所有的解題過程都是依據課本上的概念，只是將問題變了一種說法，如果想要做對，那么就要通過大量的題型訓練，使自己掌握各種題型并且應該了解需要聯系到哪一個知識點，這樣才能培養自己應對未知的疑難問題。

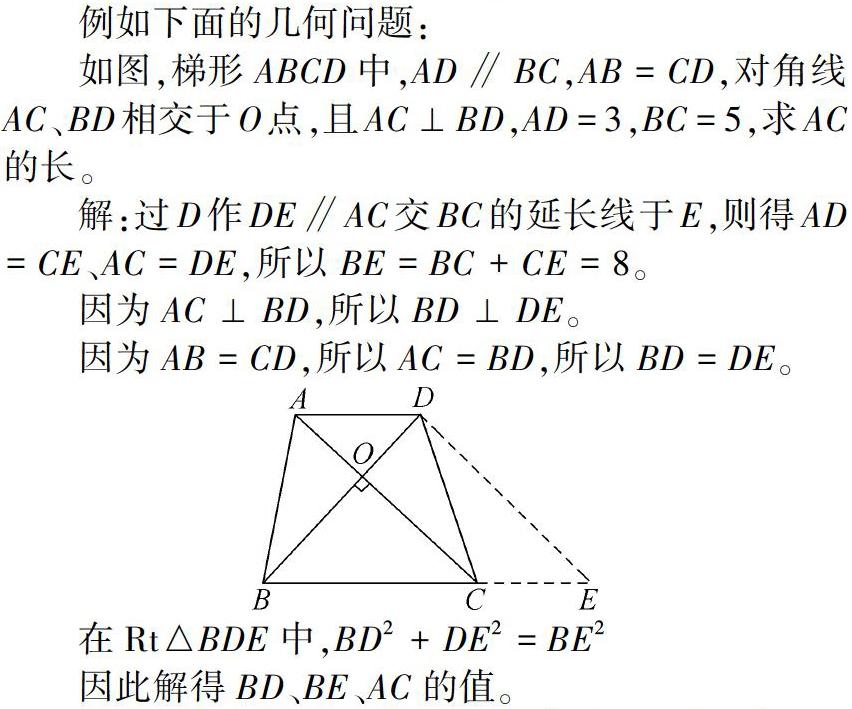
例如下面的幾何問題：

本題可根據題干中梯形對角線相互垂直的特點，轉化為直角三角形和平行四邊形，使得困難問題簡單化，進而解決問題。

三、 將化歸思想帶入高中教學課堂的有效方法

（一）要激發自己學習數學的興趣

高中數學本身就是一門枯燥無味并且抽象的學科，如果想要在高中數學上有所作為，那么每天都必須要面對那些令人頭疼的函數，一串串數字讓人找不到頭緒。要想能夠學好數學，那就一定要有較強的邏輯思維能力。對于這樣一門枯燥無味、需要較強邏輯能力的學科，需要學會培養自己的興趣，能夠調節課堂氛圍，不能將學習的好壞放在卷面表現上，而需要找到興趣點，將其與教師所教的內容相結合，從而激發學生學習的熱情，帶著這種飽滿的熱情，才能更好地掌握教師所教學的內容。

（二）重視自主學習，自主思考

新課標的改革要求關注學生的發展，越來越多的學校都從傳統的教學模式逐步走向新課改的方向。在傳統的教學模式中，大部分是以教師為主，教師是整堂課的主導力量，學生只是一個聆聽者，并沒有參與課堂來，但是這種方式會嚴重限制思維，學生只能跟隨教師的腳步去走，甚至說，有時候教師在課堂上講錯了一些知識點，并沒有人提出來，就認為是課本內容錯了，沒有人去質疑教師，如果老師不能發現錯誤，那么這種錯誤就會帶入到考試中。如果都按部就班的聽教師話，沒有人愿意主動思考，有時候一道題放在黑板上，只知道在下面等著教師給答案，并不是自己去求解，老師給出的答案也沒有人去想正不正確，都會認為教師說的都是對的，這是一種不完善的教學模式。現在，教學模式早已不是之前傳統的模式，這就需要教師把課堂大部分時間來交給學生，學生不僅僅是聆聽者，更是這個課堂的建設者。在教師的帶領下，學生要學會自己解決問題，學會質疑老師而不是百分百相信，能夠獨立解決問題，這才符合新課改下的教育觀念。教師改變傳統的教學觀念，需要主張以學生為中心開展教學任務，體現學生的重要性，給學生足夠長的時間，要客觀地評價每一個學生，要鼓勵學生積極參加到老師的日常教學中。教師要以學生為中心，制定出符合每一個學生的教學計劃，同時也要注意將化歸思想帶入到日常解題過程中，從而能夠提高主觀能動性，調動學習熱情，加強化歸思想的滲入。

四、 反思

化歸思想是高中數學解題過程中的重要思想，學生要通過平時不斷練習，不斷積累，熟練掌握化歸思想，這樣才能更好地解決高中數學中的難題。作為學生，要深掘高中教材，萬變不離其宗，所有的題考察的知識點是不變的，都是課本中的知識點，唯一變的是考察形式，要靈活運用化歸思想，將困難題型轉變成自己能夠處理的常規題型，這樣就能更好地解決高中數學的疑難問題。

五、 結束語

總結來說，化歸思想是高中解題的重要思想，如果能將化歸思想應用到高中每一道疑難題中，那么難題自然迎刃而解。學生要學著將化歸思想帶入日常解題過程中，應該充分發揮化歸思想，將大題小化，小題細化，將難題簡單化，充分發揮其積極作用。在日常解題過程中，要學會用多種思維去解題，在解每一道題目的同時，要將這道題所用的知識點列出來，日積月累，需要對各個知識點都會考察哪些題型了如指掌，即使遇到那種見都沒見過的題型，也能通過運用化歸思想輕而易舉地解出。

參考文獻：

[1]王宏利.化歸思想在高中數學解題中的應用研究[J].數理化解題研究，2020（16）：12-13.

[2]吳德發.由難化易，由繁化簡：高中數學解題過程中化歸思想的應用[J].高考，2020（2）：174.

作者簡介：汪裕佳，山東省肥城市，山東省肥城市第六高級中學。