對地指向偏差為約束的衛星平穩對日定向方法

季浩然，黃頔

（1.武漢大學 遙感信息工程學院 宇航科學與技術研究院，武漢430072；2.國防科技大學 空天科學學院，長沙410073）

衛星在軌運行過程中，根據所執行任務的不同會采用不同的姿態模式，如地面目標凝視［1］、對空間目標指向［2］、對地定向［3］、對日定向［4］等。其中，對日定向是衛星常用的姿態控制任務模式之一［5］，其通過設定衛星的期望姿態，使衛星太陽能電池陣平面充分對日以提供充足的能源。

然而，對日定向只限制了衛星姿態的2個自由度［6］，因此，在衛星對日定向的同時，還可以利用衛星姿態的另一個自由度，設定適當約束以滿足衛星其他組件、設備或載荷對衛星姿態的需求［7］。根據所附加約束的不同，對日定向又可以分為對日定向自旋穩定、以衛星速度方向偏差為約束的對日定向、以對空間目標指向偏差為約束的對日定向、以對地指向偏差為約束的對日定向等［8］。

其中，以對地指向偏差為約束的對日定向模式是一種較常見的衛星對日定向模式，其既能滿足衛星對日定向的充電需求，又能保證天線、相機等重要組件具備指向地面或地表的工作條件［9-11］。

然而，傳統的以對地指向偏差為約束的對日定向方法［12-15］，要求衛星期望對日軸嚴格指向太陽方向，同時將期望對地軸置于日-地-衛星所確定的平面內且與衛星-地心連線方向的夾角最小。依據這樣的傳統方法，在衛星-太陽連線和衛星-地球連線達到極值的前后一段短時間內，衛星期望姿態會發生大幅度翻轉。甚至當日-地-星共線時，還存在奇異現象。采用這種傳統方法，衛星期望姿態不能平穩變化，不利于衛星姿態控制系統的安全穩定，亦使得姿態控制系統頻繁高功耗工作，對衛星壽命產生損害。

為克服現有的同類方法將會導致衛星期望姿態在短時間內大幅度翻轉的奇異現象，本文提出一種平穩的以對地指向偏差為約束的對日定向方法。其核心思路為：將衛星的期望姿態設置為繞一由衛星軌道決定的基準姿態周期性地旋轉，該周期與日、地、星三者相對位置變化周期一致。首先，建立衛星的中間姿態，使得衛星的期望對地軸指向地心，衛星的期望對日軸指向軌道面法向或負法向，從而使得衛星的自由軸沿著衛星前進方向或其相反方向，且衛星的期望對地軸、期望對日軸與自由軸構成右手空間直角坐標系。其次，將衛星的中間姿態坐標系沿一歐拉軸旋轉一個角度使得期望對日軸與太陽方向偏差減小，且保證期望對地軸與對地方向的夾角不大于約束角。本文方法大幅降低了衛星的峰值期望角速度和峰值能耗，提升了衛星以對地指向偏差為約束的對日定向方法的平穩性和可靠性。

1 對日定向方法

為提供一種平穩的衛星以對地指向偏差為約束的對日定向方法，克服現有的同類方法導致衛星期望姿態在短時間內大幅度翻轉的奇異現象，本節分2步建立衛星對日定向時的期望姿態，如圖1所示。

圖1 對日定向期望姿態建立步驟Fig.1 Process of establishing expected Sun-pointing attitude

1.1 建立中間姿態

首先，依據衛星部組件布局，區分衛星的期望對地軸、期望對日軸和自由軸，同時依據任務需求設定約束角。其次，獲取衛星當前軌道位置矢量、衛星瞬時軌道面法線方向單位向量和衛星-日心連線方向矢量，并求取衛星-地心連線方向矢量。最后，建立衛星的中間姿態，使得期望對地軸指向地心，期望對日軸平行于軌道面法向，從而使得自由軸沿著衛星前進方向或其相反方向。處于中間姿態時衛星的姿態如圖2所示。

圖2 衛星中間姿態示意圖Fig.2 Schematic diagram of intermediate attitude of satellite

為便于描述，不妨以衛星本體坐標系-yb軸，即yb軸的反方向為期望對日軸，以衛星本體坐標系zb軸為期望對地軸。

特定任務中，要求衛星期望對地軸與衛星-地心連線的夾角小于一個約束角η。該約束角η表示期望對地軸和衛星-地心連線的偏差角（簡稱對地偏差角）的最大允許值，為一個約束變量。為使公式簡潔，本文取η=90°。

假設某時刻衛星的軌道位置矢量為r，衛星瞬時軌道面法線方向單位向量為n，衛星-日心連線方向單位矢量為rs，進一步可求衛星-地心連線方向的單位矢量re為

將衛星處于中間姿態時的衛星本體坐標系記為B0，并在以后的敘述中簡稱為中間姿態B0，在B0坐標系下，設定衛星本體坐標系的軸與衛星-地心連線方向單位矢量re重合，衛星本體坐標系的軸位于軌道面負法向-n，而衛星本體坐標系的指向衛星的前進方向。

中間姿態下，衛星本體坐標系坐標軸在慣性坐標系下的方向為式中：下標i為在慣性坐標系下的分量。

此時，地心慣性坐標系I到描述中間姿態的B0坐標系的轉換矩陣為

1.2 確定期望姿態

為縮小衛星期望對日軸（-yb軸）與衛星-日心連線方向的偏差角（簡稱對日偏差角），將B0進一步繞歐拉軸E旋轉ˉα角度，從而得到最終的期望姿態。記期望姿態下衛星本體坐標系為Bexp，下文簡稱期望姿態Bexp。由中間姿態旋轉至期望姿態的過程如圖3所示。

圖3 衛星期望姿態示意圖Fig.3 Schematic diagram of expected attitude of satellite

選取歐拉軸E，并計算歐拉軸E在B0坐標系下的投影E0。慣性坐標系I下歐拉軸E可由式（4）確定：

進而可計算得到B0坐標系下歐拉軸E的投影E0為

式中：下標0為在B0坐標系下的分量。

計算中間姿態下期望對日軸與衛星-日心連線方向的夾角，并定義為對日偏差角，即本文中-yb0軸與rs的夾角為α，則

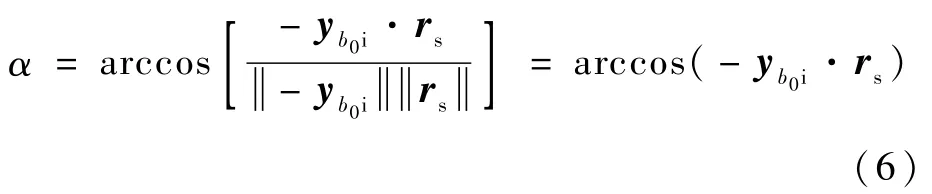
為確保Bexp姿態下軸與re的夾角（以下簡稱對地偏差角）不大于給定的約束角η，一定情況下，歐拉角需小于某一旋轉約束角β。所述旋轉約束角β為當中間姿態繞歐拉軸旋轉而導致期望對地軸與衛星-地心連線的角度恰等于約束角時，中間姿態繞歐拉軸所轉過的角度。在本文中，當與的夾角恰好等于約束角η時，B0繞歐拉軸E轉過的角度即為β。

在坐標系B0下，λ的值由式（8）可得

根據幾何關系，旋轉約束角β可以由夾角λ和約束角η唯一確定。注意到，本文中η取為直角，運用余弦定理，易得本文中旋轉約束角β簡化為

繞歐拉軸E旋轉的歐拉角αˉ的確定原則如下：當衛星中間姿態繞歐拉軸進行任意旋轉，對地偏差角均不會大于約束角時，旋轉約束角無解，此時，旋轉角度取式（6）所確定的中間姿態下的對日偏差角；當衛星中間姿態繞歐拉軸進行旋轉，存在對地偏差角大于約束角的情形時，旋轉約束角有解，此時，旋轉角度取中間姿態下的對日偏差角α與式（9）確定的旋轉約束角β中的較小值。

實際應用中，約束角的取值應綜合考慮相機視場角、天線波束角等約束，并利用球面三角公式對式（9）重新求解。作為對比，傳統方法雖然沒有約束角的概念，其實際對地偏差極大值為90°并且無法人為減小。約束角的取值可以自定義亦是本文方法的優勢之一。

根據四元數的性質，直接得到B0坐標系轉至Bexp坐標系的轉換矩陣為

由此得到由慣性坐標系I轉換至期望姿態坐標系Bexp的轉換矩陣為

因此，期望姿態坐標系Bexp在慣性坐標系I下的空間指向可以由式（13）確定。也可以說，由慣性坐標系I至期望姿態下衛星本體坐標系Bexp的轉換矩陣唯一確定了衛星期望姿態在慣性坐標系下的描述。

2 數值仿真

2.1 平穩對日定向方法

依據本文所提出的對日定向方法，在J2軌道動力學仿真條件下進行仿真。設定航天器位于485 km高度的35°傾角LEO軌道。為充分檢驗本文對日定向方法的有效性，將仿真場景時間設為2019年1月1日至2020年7月1日，共計1.5年。得到計算結果如圖4～圖9所示。

圖4為1.5年的仿真時間段內，衛星期望對地軸與實際衛星-地心連線方向的夾角變化。可知，采用本文對日定向方法，衛星對地偏差角被有效限制在90°約束角范圍以內。

圖5為1.5年的仿真時間段內，衛星期望對日軸與實際衛星-日心連線方向的夾角變化。可知，采用本文對日定向方法，會部分犧牲衛星對日定向的效能，即存在對日偏差角不為零的情況，衛星對日偏差角峰值約為57°。

為進一步考察采用本文平穩對日定向方法后，衛星對日定向的效能損失，截取圖5中2019年1月22日0：00～6：00的一段非零對日偏差角密集區局部放大，對日偏差角的變化規律如圖6所示。

圖4 對地偏差角在1.5年時間內的變化規律Fig.4 Development of deviation of Earth-pointing within 1.5 years

圖5 對日偏差角在1.5年時間內的變化規律Fig.5 Development of deviation of Sun-pointing within 1.5 years

在圖6所示仿真時段中，對日偏差角為零的時段約占整個仿真時段的55%，而對日偏差角的峰值約為54°。綜合圖5～圖6所示對日偏差角變化規律可以發現，采用本文以對地指向偏差為約束的衛星平穩對日定向方法后，衛星對日偏差角被較好地控制，期望對日軸在多數時間能夠嚴格地對日定向。

采用本文提出的平穩對日定向策略后，衛星在1.5年內的期望角速度變化如圖7～圖9所示。衛星期望角速度平穩變化，x方向和z方向的角速度最大值不超過0.3（°）/s，y方向的角速度穩定在0.065（°）/s，y方向的角速度與衛星軌道角速度保持一致。

對比圖5和圖7～圖9可以發現，衛星期望角速度的變化規律與對日偏差角的變化規律同步，即當對日偏差角的局部極值越大時，衛星期望角速度的局部極值也越大。而當衛星對日偏差角在一段連續時間內能夠保持為零時，航天器在該段區間內的期望角速度亦保持為低值，僅需繞y方向保持低速自旋，自旋周期與軌道周期一致。

圖6 連續6小時內對日偏差角的變化規律（2019年1月22日）Fig.6 Development of deviation of Sun-pointing within consecutive 6 hours（2019-01-22）

圖7 依據期望姿態差分得到的衛星x軸角速度Fig.7 Angular velocity in x-axis obtained by difference of expected attitude

圖8 依據期望姿態差分得到的衛星y軸角速度Fig.8 Angular velocity in y-axis obtained by difference of expected attitude

2.2 傳統對日定向方法

為了更好地說明傳統對日定向方法導致的期望姿態短時間內大角度翻轉的奇異現象及其機理，采取同樣的仿真條件，采用傳統的對日定向方法進行仿真。依據傳統對日定向方法，設定衛星-yb軸嚴格指向太陽的同時，zb軸與衛星-地心連線方向的夾角最小，zb軸位于星-地連線與對日方向共同確定的平面上。

圖10給出了1.5年的仿真時間段內衛星-地心連線和衛星-日心連線的夾角往復變化。可以看出，圖中頻繁出現了接近零或180°的奇異區間。這種奇異區的存在，將導致期望姿態在短時間內大幅度變化，從而導致衛星期望角速度過大。如圖11所示，如果采用傳統的對日定向方法，衛星期望角速度在奇異區出現突變，其峰值大于15（°）/s，不利于衛星節能和安全防護。

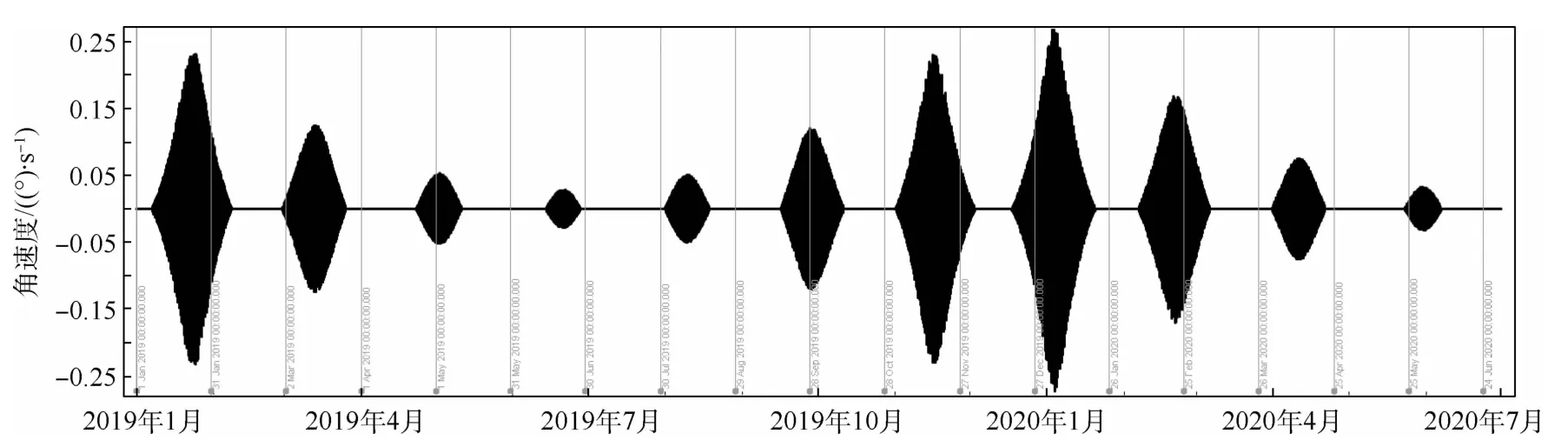
圖9 依據期望姿態差分得到的衛星z軸角速度Fig.9 Angular velocity in z-axis obtained by difference of expected attitude

圖10 衛星-地心連線和衛星-日心連線夾角的變化規律Fig.10 Development of included angle between the satellite-Earth vector and the satellite-sun vector

圖11 傳統對日定向方法在1.5年時間內對期望姿態差分得到的角速度Fig.11 Angular velocity obtained by difference of traditional expected attitude with 1.5 years

3 結束語

本文提出了一種衛星平穩對日定向方法。由于采用了中間姿態過渡，衛星期望姿態和期望角速度得以平穩變化，在不顯著犧牲衛星對日定向效能的前提下，克服了衛星期望姿態快速翻轉的奇異現象，并且能夠嚴格確保對地偏差角小于所設計的約束角，大幅降低了衛星的峰值期望角速度和峰值能耗，提升了衛星以對地指向偏差為約束的對日定向方法的平穩性和可靠性。