近海廢棄物收集系統壓縮裝置的疲勞壽命分析＊

青島科技大學機電工程學院 青島 266061

0 引言

當前，我國機械裝備制造業迅猛發展，工藝水平得到長足進步，對裝備的耐疲勞性提出了更高要求，故對機械裝備的疲勞壽命研究具有重要意義[1]。一些科研機構及公司著手研究船體裝備的疲勞壽命，Vedeler首先提出了船體疲勞強度的危害性[2]；Jordan 和Cochran對多艘正在服役船舶進行檢測，在多艘船舶的關鍵區域發現了疲勞裂紋[3，4]；Song R等基于概率斷裂力學理論提出一種雙體船簡化疲勞分析方法[5]；CCS的王然章川等人對船體結構疲勞強度計算的簡化方法進行了研究[6]；蔣志巖對船體結構疲勞評估過程中的應力分析方法進行了探討和比較，并通過有限元軟件對熱點應力的插值方法和有限元建模原則進行了研究[7]；顧學康、沈進威對非線性載荷的計算及其對疲勞損傷的影響進行了研究[8]。

由此可知，目前國內外針對船體結構的疲勞壽命研究較多，而對船體裝置內部結構的疲勞壽命研究較少[9]。在近海廢棄物收集船的壓縮裝置中，推板是實現壓縮和推送垃圾的重要部件。壓縮裝置在工作過程中，推板會承受變化的動載荷，并在其作用下產生動態應力。當推板運行到保壓階段時，疲勞強度會降低，產生疲勞裂紋[10]，最終有可能導致推板發生斷裂破壞。因此，有必要對推板進行疲勞壽命分析，確保推板結構在滿足強度和剛度要求的基礎上，達到可靠性和壽命要求。

1 壓縮裝置的結構

近海廢棄物收集系統中的壓縮裝置主要由滑軌、進料斗、推板、液壓缸、壓縮艙體等組成，壓縮裝置結構示意圖如圖1所示。推板由板材制成，整體呈折面形，存在一個傾斜的支撐面；推板的側面設置3個液壓缸基座安裝點，并通過焊接形式連接推板與液壓缸基座；左右兩側布置滑軌接觸口，并將推板與滑塊整體焊接；推板底部施加3個排水孔，排水孔貫穿整體推板。壓縮裝置推板結構的三維模型如圖2所示。

圖1 壓縮裝置結構示意圖

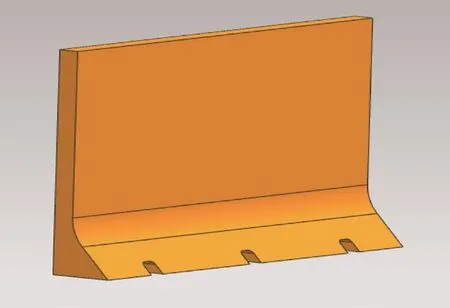
圖2 推板三維模型

2 推板的靜力學分析

靜力學分析為推板疲勞壽命預測提供應力應變歷程結果，確定疲勞問題較嚴重的部位[11]。靜力學分析結果的可靠性將影響推板疲勞壽命預測結果的準確性，故有必要進行靜力學分析。利用Ansys Workbench仿真平臺對推板進行靜力學仿真分析，首先將推板三維模型導入仿真平臺，并對模型進行網格劃分；然后依據推板的受力情況對模型施加載荷與約束；最后對模型的仿真分析進行求解，得到推板在理論載荷和約束下的變形和應力云圖，完成靜力學仿真。

2.1 理論基礎與參數設置

1）理論基礎

采用有限元法對結構進行靜力學分析，對整體結構進行受力分析和結構簡化,利用離散化的方法把簡化的連續結構看作許多單元組件。對每個單元建立剛度方程,對整體結構建立平衡方程[12，13]。通過研究物體在力系作用下的平衡規律,確定靜力學分析理論公式為

式中：[K]為剛度矩陣，{x}為節點位移矩陣，{F}為戴荷矩陣。

2）參數設置

設置材料屬性，選擇推板材料為Q345，其抗拉強度為490 MPa，屈服強度為345 MPa，彈性模量為2.06×105MPa，密度為7.85×10-6kg/mm3，泊松比為0.28。將有限元模型導入Ansys Workbench仿真平臺，對模型劃分網格，將載荷和約束施加于推板，推板的受力主要有執行液壓缸對推板的推力、廢棄物對推板的作用力、廢棄物對傾斜面的作用力等。如圖3所示，在液壓缸基座B、C、D處分別施加載荷，在推板A點處設置固定約束。

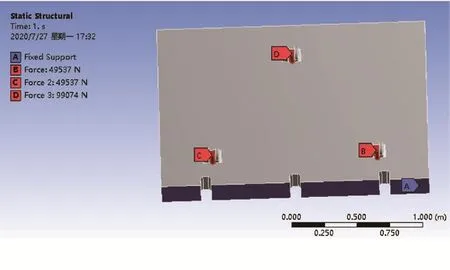
圖3 推板載荷與約束圖

2.2 結果分析

前處理完成后，對推板模型仿真分析求解得到推板應力應變云圖，推板的變形情況如圖4所示，推板的應力分布情況如圖5所示。

圖4 推板應變云圖

由圖4可以看出，推板的變形主要發生在X方向，其變形數值為3.88 mm，Y方向和Z方向的變形較小，分別為0.42 mm和0.11 mm。推板的最大變形位置集中在推板中上部，變形量的變化規律呈環狀分布，由內圈向外圈逐漸降低。

由圖5可得推板最大的受力區域位于推板的頂部區域，存在應力集中現象，推板下部的受力較小，所受的最大應力值為242.35 MPa，低于推板材料的屈服強度，與實際工況相符，推板結構強度符合設計要求。

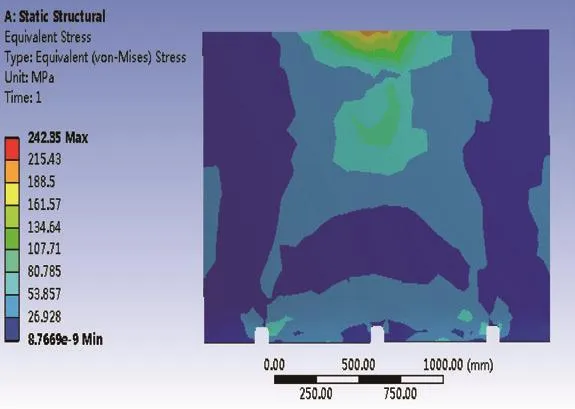
圖5 推板應力云圖

2.3 推板的改進

由前述推板靜力學仿真結果可知，推板在X方向的變形相對較大，且最大變形位置集中在推板頂部。為保證推板的安全性，對其結構做出改進，在安裝液壓缸基座的一側中上部設置加強筋。將改進后的分析模型導入Ansys Workbench中，對模型施加載荷與約束。如圖6所示，在強筋A處施加固定約束，分別在液壓缸基座B、C、D三處施加載荷。參照前文對推板的靜力學分析步驟，完成對改進后推板的靜力學分析。

圖6 改進后的推板載荷與約束圖

對改進后的推板進行仿真分析所獲得推板最大變形量為3.07 mm，主要變形發生在X方向，變形規律由中心向四周擴散，相比較改進前的推板變形量減少0.81 mm；改進后推板的應力主要集中在推板的中上部，最大應力為 258.38 MPa，小于設計材料的最大許用應力，故在強度上推板足夠安全。

3 疲勞壽命分析

Ansys疲勞分析是基于Miner法則進行的，以推板靜力學分析結果為基礎，對推板進行疲勞壽命分析。根據推板應力應變情況可知，改進后的推板形變量減小。由于形變量對推板疲勞破壞影響較小，故本文重點分析推板基于高周疲勞下的疲勞壽命。

3.1 疲勞分析方法

本文基于Miner累積損傷理論應用有限壽命設計法對壓縮裝置的推板進行疲勞特性分析。Miner累積損傷理論描述了循環載荷對結構的持續作用，使結構發生損傷進而產生疲勞破壞。材料產生疲勞損傷的程度與應力的循環次數呈正相關，結構的疲勞損傷累積達到破壞時吸收的凈功W與疲勞載荷歷史無關。假定在某級應力下，材料產生破壞，其應力循環次數為N1，W表示吸收能量的極限，在經過n1次應力循環后，材料產生的疲勞損傷吸收的凈功為W1，則根據Miner累積損傷理論可得

材料的疲勞累積損傷由式（3）可得

式中：ni為第i級應力水平級別下經過的應力循環次數；Ni為第i級應力水平級別下結構達到破壞時候的應力循環數。

由式（3）可知，當D的數值等于1時，評定對象開始出現破壞。

3.2 疲勞特性

在設計仿真中，疲勞分析模塊需要用到在工程數據分支下的材料特性當中的S-N曲線數據。因此，在進行疲勞分析前，需對疲勞材料特性進行添加和修改，并在材料特性的工作表中插入S-N曲線。S-N曲線表示材料所受的應力幅與失效循環次數之間的關系[14],通常情況下的S-N曲線是由疲勞測試得到的，參考GB/T 3075—2008《金屬材料疲勞試驗軸向力控制方法》，對相關文獻中應用統計學法和升降法得到的數據進行分析，將數據輸入材料特性的工作列表，得到圖7所示雙對數曲線。

圖7 雙對數S-N曲線

由圖7可知，在給定的應力比下，應力范圍S越小，壽命越長。當應力范圍S小于某極限值時，試件不發生破壞，壽命趨于無限長。

3.3 仿真設置

對疲勞工具Fatigue tool進行初始設置，在初始設置中，對疲勞載荷類型進行定義。由于推板承受的是循環載荷，故在設置中選擇類型為Fully Reversed，對于交互應力循環不需考慮平均應力理論；在Fatigue Tool中添加Life、Safety Factor、Fatigue Sensitivity命令；通過Life模塊，選擇Evaluta all Results計算。

3.4 結果分析

推板在循環載荷作用下的疲勞壽命云圖如圖8所示。圖中推板在循環載荷作用下的最大疲勞壽命值為9.7×106次循環，最小值為9.2×106次循環，滿足設計要求。推板在循環載荷作用下的安全因子云圖如圖9所示。

圖8 疲勞壽命云圖

圖9 安全因子云圖

由圖9可知，推板的最小安全因子為1.335 2大于1，最大安全因子為15，故推板整體結構較為安全。

在臨界區域內，部件的壽命、損傷或安全系數等參數隨載荷的變化而變化，這種變化情況通過疲勞壽命曲線圖得以體現，如圖10所示。

由圖10可知，當最大基本載荷擴大范圍為0.5～1倍時，疲勞壽命值基本保持不變；當最大基本載荷擴大1倍，疲勞壽命值驟減，下降幅度變大；當最大基本載荷擴大到1.1倍，疲勞壽命循環次數為4.1×105次。推板在循環載荷作用下的雙軸指示結果如圖11所示。

圖10 疲勞壽命曲線

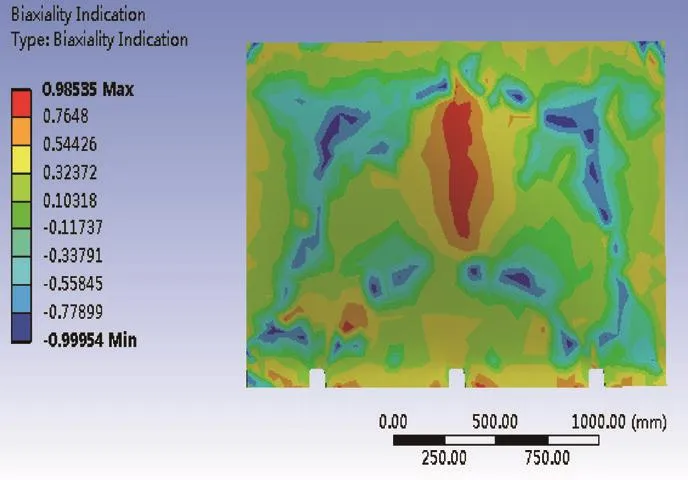
圖11 雙軸指示結果

由圖11可知，推板所受應力值最大區域在中上部位置，集中在推板與液壓缸基座焊接處，與靜力學應力仿真結果相對應。因此，在對推板進行設計時，應注重與推板相連的液壓缸基座處的設計，此處產生疲勞裂紋的可能性較大，疲勞裂紋會直接影響推板的疲勞壽命。

4 結論

1）靜力學分析結果表明，改進前推板的變形量為3.88 mm，變形相對較大；改進后推板的最大變形量為3.07 mm，最大應力為 258.38 MPa。最大應力小于設計材料的最大許用應力，故在強度上推板是足夠安全，產生的應力主要位于推板中上部。

2）疲勞壽命分析結果表明，推板在循環載荷作用下的最大疲勞壽命值為9.7×106次，最小值為9.2×106次。將最大基本載荷擴大1.1倍后，推板的疲勞壽命循環次數降為4.1×105次；與推板相連的液壓缸基座處所受應力最大，產生疲勞裂紋的可能性最大；整體來看，推板結構較為安全。