“數(shù)直線”在小學數(shù)與代數(shù)領域教學中的思考與實踐

劉瑋瑋 齊 晨

（北京市海淀區(qū)五一小學 北京 100039）

2011版《數(shù)學課程標準》明確指出：在數(shù)學課程中，應當注重發(fā)展學生的數(shù)感、符號意識、幾何直觀、運算能力和模型思想等。在“數(shù)與代數(shù)”領域的教學中，教師可以借助直觀模型讓學生認識數(shù)、表示數(shù)、比較數(shù)的大小并對數(shù)進行運算，提高課堂實效性。學生在借助直觀模型解決問題的過程中，獲得活動經(jīng)驗，發(fā)展數(shù)感及運算能力。因此，本文以“數(shù)直線”這一直觀模型為例，試圖梳理了數(shù)直線模型在小學教學中的編排情況及實踐應用。

1 對數(shù)直線模型的認識

所謂直觀模型，王長沛教授有過這樣的論述：“結(jié)構(gòu)化的學習材料”。也就是，在認識數(shù)、對數(shù)進行運算的過程中，在滿足學生需求的條件下，具備數(shù)的組成結(jié)構(gòu)十進制特征的學習材料。在小學數(shù)學階段，教材呈現(xiàn)了大量的直觀模型幫助學生加深對數(shù)的認識，提升運算能力，例如：小棒、計數(shù)器、人民幣、數(shù)直線模型等。

在這些直觀模型中，數(shù)直線模型較為特殊。數(shù)直線模型是“數(shù)軸”的雛形，它作為一種形象化的工具，將“數(shù)”與“形”完美結(jié)合，建立起“數(shù)”與“點”的一一對應關系。學生借助數(shù)直線可以直觀的認識數(shù)，發(fā)現(xiàn)數(shù)與數(shù)之間的聯(lián)系。同時，學生可以感受數(shù)直線所具備的連續(xù)性，逐漸體會數(shù)域的形成及擴展過程。

因其自身特點，數(shù)直線在數(shù)與代數(shù)領域?qū)W習中有著較為廣泛地應用，很好地支撐了學生對數(shù)的認識和運算的理解。雖然數(shù)直線能夠清晰直觀的表示對應關系，但從某種程度上講，數(shù)直線的抽象對于小學生而言是相對困難的地方。因此，在使用數(shù)直線模型的過程中，我們需要考慮到直觀模型的優(yōu)勢，可以引用數(shù)直線把抽象的“數(shù)”以“形”的形式體現(xiàn)。同時，需要考慮小學生的知識及年齡特點，進行有效篩選、編排，找到適合的教學內(nèi)容，再采取數(shù)直線模型來輔助教學，逐步促進學生數(shù)形結(jié)合思想的發(fā)展。

2 數(shù)直線在教材中的編排情況

由于數(shù)直線模型本身具有一定抽象性，為了符合學生的成長邏輯。思維層面，在教材的編排上，學生經(jīng)歷從“實物圖”到“數(shù)尺”再到“數(shù)直線”抽象的過程，逐漸感悟數(shù)直線的應用價值，抽象數(shù)學本質(zhì)，感悟數(shù)學思想。知識層面，無論是認識數(shù)還是運算數(shù)的過程，都積極引導學生在線上找到數(shù)，適時將“數(shù)”與“形”進行有機結(jié)合。在認識數(shù)本身和比較數(shù)大小的過程中，教材也注意引導學生借助數(shù)直線從自然數(shù)逐漸擴充到小數(shù)、分數(shù)的認識和比較。學生能夠直觀的感受數(shù)域擴充的過程，深化認知。

2.1 數(shù)認識領域

2.1.1 認識數(shù)本身

在小學階段，在認識數(shù)的過程中，無論是自然數(shù)、小數(shù)、分數(shù)還是正負數(shù)，都會借助數(shù)直線模型來呈現(xiàn)。通過對北師版教材的梳理，我們發(fā)現(xiàn)教材的編排意圖不僅僅停留在認識數(shù)直線，而充分將“數(shù)”與“形”結(jié)合，借助數(shù)直線來直觀的認識數(shù)，觀察數(shù)的特征，從而關注到數(shù)與數(shù)之間的內(nèi)在關聯(lián)。

尤其是在分數(shù)意義的教學中，學生經(jīng)歷了將單位“1”平均分的過程，找到相應份數(shù)，從而用分數(shù)表示。本單元的教學中難點在于學生容易忽略了分數(shù)本身就是一個數(shù)，教材此時讓學生在數(shù)直線上標出分數(shù)，使其“數(shù)”的身份直觀地得以外顯。

2.1.2 比較數(shù)大小

學生在認識數(shù)之后，將會對數(shù)進行比較大小。由于數(shù)直線自身的特點，它能夠直觀、清晰地體現(xiàn)出“數(shù)”與“點”在“線”上一一對應的關系。同時，數(shù)直線一般規(guī)定向右為正方向，也就是在直線上的數(shù)越往右數(shù)就越大。便于學生觀察數(shù)的大小，對數(shù)進行比較，逐步發(fā)展數(shù)感。

2.1.3 極限思想

在小數(shù)部分教學中，學生理解0.1與0.2之間有無限個小數(shù)是教學難點，這其中蘊含了極限思想。那么對于這樣抽象的問題，學生理解是必然有難度的。這就需要教師采用直觀的方法來將此問題進行外顯，此時數(shù)直線就可以清晰地表示這個過程。學生可以在數(shù)直線上無限地進行平均分，平均分得越精細，得到的小數(shù)單位就越小，最終借助數(shù)直線將極限思想外顯。

在數(shù)比較的過程中不僅有大有小，還有相等的可能，那數(shù)直線中可以表示相等的數(shù)嗎？答案是肯定的。數(shù)直線可以清晰的表示等值分數(shù)，學生能夠快速地找到四分之一、八分之二、十二分之三等，然后清晰地發(fā)現(xiàn)他們在數(shù)直線上的“點”是一致的，也就直觀地感受到了這三個分數(shù)是等值的。小數(shù)部分也同樣如此，學生能夠一目了然地看到0.1、0.10、0.100在數(shù)直線上的位置，發(fā)現(xiàn)無論后邊添多少個0，數(shù)值都是一樣大的。

2.2 數(shù)運算領域

2.2.1 外顯運算本質(zhì)

數(shù)直線在四則運算中也發(fā)揮著不可替代的作用。四則運算的意義是較為抽象的，而對于小學階段的學生而言，這樣的抽象對于他們本身就是一個難點，同時還要面對遇到問題選擇恰當?shù)倪\算法則，這就需要對四則運算的意義極為理解。那么面對抽象的意義學習就需要用數(shù)直線這樣的直觀模型來刻畫。在梳理教材中對于四則運算意義的編排可以發(fā)現(xiàn)，數(shù)直線作為直觀模型來輔助數(shù)的運算，它將運算的過程直觀呈現(xiàn)，讓運算的本質(zhì)外顯。

2.2.2 勾連運算關系

在小學生的運算中，加減乘除四種運算各自有各自的意義，但是它們不是孤立存在著，它們的運算意義之間具有密切的內(nèi)在聯(lián)系。而這種內(nèi)在聯(lián)系，小學生理解起來并不像我們想象的那樣容易，此時我們不妨把它放在數(shù)直線上，讓學生逐步感受，引發(fā)他們產(chǎn)生對四種運算內(nèi)在關聯(lián)的思考。

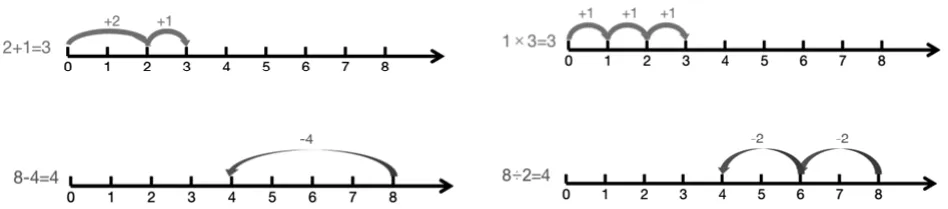
如上圖，在數(shù)直線上，加法就是向正方向不斷累加的過程，當在數(shù)直線上逐漸向正方向按相同距離累加時就延伸出了乘法的意義；如果將數(shù)向相反的方向減少（距離可等可不等），就產(chǎn)生了減法，而除法就可以理解為這樣的反方向、等距離減少。因此，數(shù)直線可以直觀地使學生觀察到每種運算的過程，很好地外顯出四則運算的內(nèi)在聯(lián)系，有效發(fā)展學生的運算能力。

3 數(shù)直線在實踐中的應用

3.1 在課堂學習中的應用

3.1.1 低年級加減法問題中的應用

在北師大版二年級下冊加與減單元中，教材編排了三位數(shù)加與減的方法教學。在直觀模型的使用中，教材著重滲透了數(shù)直線的使用。例如“453+129=”，首先引導學生在數(shù)直線上的起點標為453，再將129拆分成100、20和9，同時引導學生在數(shù)直線上注意100、20和9的距離長短，最終依次累加找到答案。在這個過程中，不僅關注到了數(shù)直線的使用，還關注到了將“數(shù)”用“形”的形式外顯，最終解決問題。同時，引導學生在累加的過程中注意距離的長短，發(fā)展運算能力的同時，借助直觀來培養(yǎng)學生的數(shù)感。

3.1.2 近似數(shù)的學習

（1）四舍五入。在小學階段，“四舍五入”求取近似數(shù)是學生心中的一種規(guī)則。到底為什么會有這樣的規(guī)則？為什么要求取近似值時要“四舍五入”？其實，學生是不能理解的。而“四舍五入”的背后是有道理的，我們應該讓孩子們?nèi)ジ惺堋⑷ンw會，從而理解“四舍五入”的本質(zhì)。因此，我們嘗試用數(shù)直線幫助學生理解求近似數(shù)時“四舍五入”的方法。以下是教學中的一個活動，這個活動內(nèi)容在于讓學生借助數(shù)直線理解“大約40人”的含義：

教師：咱們年級有一個班大約40人，你覺得他們班可能有多少人？請你認真思考，試著在黑板上的數(shù)直線中標一標，并說說你的想法。

預設①：我標了39，因為39離40比較近。

預設②：我標了38，因為38離40只差兩人。

……

預設③：我標了34，我覺得34也有可能。

教師追問：34真的可以嗎？

預設：我覺得不可以，因為我們從數(shù)直線上觀察到34離30更近一些。

教師追問：還有其他想要補充的嗎？

預設④：那35到底是近似成30還是40呢？我從數(shù)直線中看到，35離30或者40的距離是一樣的。這該怎么辦呢？

教師：那我們?yōu)榱朔奖悖覀兌ㄒ粋€規(guī)則進行統(tǒng)一，我們把35近似成40。

預設⑤：我明白了！45雖然離40和50的距離是一樣的，但按照剛才的規(guī)則，我們把45近似成50。

預設⑥：所以能夠近似成40的數(shù)分別是44、43、42、41、39、38、37、36、35。

設計意圖：本環(huán)節(jié)通過學生間的合作學習討論，讓學生感受到“四舍五入”方法的來源，加深本身對近似數(shù)的認識，在這個過程中借助數(shù)直線模型讓學生初步感知數(shù)域。

在教學中，我們借助數(shù)直線直觀從接受規(guī)則到自主生發(fā)，“四舍五入”水到渠成，最終理解“近似數(shù)”的實質(zhì)。同時，在這個過程中學生從能夠主動產(chǎn)生“四舍五入”的需求。這個過程，已經(jīng)悄無聲息地讓學生心中的“規(guī)則”轉(zhuǎn)變成了“需求”。

（2）截取近似數(shù)難點（最大值、最小值）。在近似數(shù)部分的學習中，學生對于尋找一個具體數(shù)的最大、最小近似數(shù)是難點。學生經(jīng)常在“忽略‘四舍’、找不到真正的極值”等問題出現(xiàn)錯誤。因此，我們借助數(shù)直線直觀地將“數(shù)”與“形”結(jié)合，嘗試突破難點。教學前，學生在潛意識里認為，數(shù)直線上標出2萬的近似數(shù)是點狀的，而在實際學習過程中他們逐步認識到，其實這些點是連續(xù)的，是密集存在的，是可以從區(qū)間（區(qū)域）的角度去思考以及認識的。這是一個新的視角，一次新的成長！因此我認為，近似數(shù)的學習是學生對數(shù)認識的一次飛躍——從“點狀分布”認識飛躍到“區(qū)間線狀分布”認識。以下是教師在具體課堂教學實踐過程中的主要環(huán)節(jié)設計以及師生的交流情況：（見表1）。

表1

學生首先在數(shù)直線直觀找到20000左右的兩個數(shù)可能是近似數(shù)。在教師的引導下，學生逐漸直觀發(fā)現(xiàn)20000的近似數(shù)有無限多個，同時還能在數(shù)直線上找到一一對應。學生在這個從點狀分布逐漸探究到線狀分布的過程中，借助數(shù)直線模型發(fā)展學生的極限思維。一條數(shù)直線讓學生從有限個數(shù)發(fā)展到無限個數(shù)，思維上從“點”勾連到“線”，從“線”上升到“范圍”。

3.1.3 正負數(shù)的認識

（1）認識意義。對于小學階段“數(shù)與代數(shù)”部分的知識內(nèi)容來說，負數(shù)的認識與之前其他數(shù)的認識不同。它會讓學生看到之前學習的所有數(shù)都可以找到與之意義相反的數(shù)。對于負數(shù)認識本身而言，學生的正確認識以及充分理解會直接作用于他們對正數(shù)的理解，并進一步豐富、加深對前面所學內(nèi)容的認識。在認識負數(shù)的教學過程中，教師既要從生活中引入負數(shù)，還要讓學生直觀地看到負數(shù)的所在位置。因此，數(shù)直線作為一條直線，它可以向反方向無限延長，這一特點能夠幫助學生直接在線上找到對應的點來表示負數(shù)。學生經(jīng)歷在數(shù)直線上找負數(shù)的活動經(jīng)驗后，將會對正數(shù)、負數(shù)的意義理解得更深刻。

（2）三個“蘊伏”。基于負數(shù)本身的特點，它與正數(shù)是不可分割的，需要捆綁在一起進行研究。然而對于正負數(shù)的學習主要處在初中階段，那么對于小學階段學生能否主動產(chǎn)生對正負數(shù)的感知呢？答案是一定的。在小學階段，負數(shù)教學中數(shù)直線模型蘊伏著相反數(shù)、絕對值和正負數(shù)運算的認識。

負數(shù)自身具有豐富的內(nèi)涵，在小學學習中可以借助數(shù)直線予以適當蘊伏，為后續(xù)學習奠定基礎。在教學中，當學生將一些正負數(shù)標在數(shù)直線上時，教師引導學生觀察（如圖1）：它們到0的距離誰更遠？誰更近？適時蘊伏絕對值；教學中，教師有意識地引導學生將相反數(shù)一對一對地標在數(shù)直線上（如圖2），使學生直觀看到其與原點“0”的距離相同，蘊伏相反數(shù)；在充分觀察交流正負數(shù)的過程中，蘊伏正負數(shù)運算（如圖3）。

3.2 在學習評價中的應用

數(shù)直線的使用不僅存在于課堂教學中，在評價中也能看到數(shù)直線模型的身影。然而數(shù)直線不是應用于評價中，而是在應用中借助它來考查學生對于數(shù)本身、數(shù)運算的認識。例如在從教材的編排以及海淀區(qū)七年級監(jiān)測的試卷中均有涉及。

以海淀區(qū)七年級監(jiān)測為例進行說明：本題考察了學生對小數(shù)、分數(shù)數(shù)值大小的判斷及四則運算意義的理解。如果不借助數(shù)直線模型進行評價，可能會出現(xiàn)填比較符號判斷數(shù)值大小，將所給數(shù)進行排隊等題型。當把這些“數(shù)”放在數(shù)直線上，讓這個“數(shù)”的大小通過它體現(xiàn)出來。“m、n”在0和1之間，那它們一定是大于0小于1的小數(shù)或者真分數(shù)。同時，借助數(shù)直線進行評價，“m、n、t”本身沒有具體數(shù)字，學生需要根據(jù)圖意進行設數(shù)或者真正結(jié)合四則運算意義出發(fā)判斷數(shù)值大小。這種抽象的考察方式，對于學生來說是對數(shù)的認識、四則運算意義的真正理解。這些都是學生在數(shù)直線中提取到的數(shù)學信息。而提取這些信息的過程，就是學生對于數(shù)的認識。

而學生們這些認識就是源自于平時練習中把“數(shù)”放在數(shù)直線上，將“數(shù)”與“形”結(jié)合角度理解數(shù)和運算。因此，評價是一種教學導向，測查學生學習能力的一種方式。作為教師，隨著學生年齡的增長，我們也需要借助數(shù)直線模型幫助學生更深入理解數(shù)、理解運算意義，最終提升運算能力和數(shù)感。

4 寫在最后

數(shù)直線這一直觀模型很好地支撐了學生對數(shù)意義以及數(shù)運算的認識與理解，可以使學生的學習有機會向縱深處不斷邁進。數(shù)直線是數(shù)軸的雛形，而數(shù)軸在學生的后續(xù)數(shù)學學習中具有重要的價值。小學階段數(shù)直線的理解與運用會為學生積累寶貴的學習經(jīng)驗，因此我們在教學中要給予應有的重視，適時引導學生應用數(shù)直線表達思考，深入探究。與此同時還要注意不要將數(shù)直線過早地抽象到數(shù)軸的高度，在應用數(shù)直線的過程中，也不要過早地讓數(shù)直線模式化。我們可以適時引導學生在學習過程中進行有效創(chuàng)造，使他們能夠更豐富、更深入地理解、認識以及解決問題。

通過對數(shù)直線的思考與課堂實踐，我發(fā)現(xiàn)：一條簡簡單單的數(shù)直線，架起了抽象與直觀之間的橋梁，數(shù)與數(shù)之間的橋梁，知識與經(jīng)驗之間的橋梁，能力與思維的橋梁，對提升學生的數(shù)學核心素養(yǎng)發(fā)揮了積極而重要的作用。作為教師的我，也在數(shù)直線的研究中與孩子們一起真切地體驗著，真實地收獲著，不斷地成長著……