計算Lyapunov指數(shù)的模糊C均值聚類小數(shù)據(jù)量法

高允報，孫玉泉

(北京航空航天大學(xué)數(shù)學(xué)科學(xué)學(xué)院，北京 100191)

Lyapunov指數(shù)(LE)可以判斷動力系統(tǒng)的混沌狀態(tài)，在研究混沌運動特性中起著非常重要的作用，是衡量動力學(xué)特性的一個重要定量指標(biāo)，它表征了系統(tǒng)在相空間中相鄰軌道間收斂或發(fā)散的平均指數(shù)率[1].系統(tǒng)的混沌狀態(tài)可以通過LE的正負來判斷，所以研究如何計算LE就非常必要.

近年來國內(nèi)外學(xué)者對LE的計算方法做了很多研究.嚴(yán)雯等[2]利用定義法求解了Logistic模型的最大Lyapunov指數(shù)(LLE)；Wolf等[3]利用Wolf法計算出幾種混沌系統(tǒng)的LLE；Rosenstein等[4]提出小數(shù)據(jù)量法來計算LLE.然而定義法只適用于計算已知系統(tǒng)的LE；Wolf法計算LLE時過程較為復(fù)雜且結(jié)果往往不精確；小數(shù)據(jù)量法在不知系統(tǒng)方程而僅可獲得離散數(shù)據(jù)的情況下計算LLE時，對于線性區(qū)域的判斷往往通過直觀觀察，導(dǎo)致結(jié)果誤差較大.本文將模糊C均值聚類算法用于小數(shù)據(jù)量法線性區(qū)域的選擇，提出了模糊C均值聚類小數(shù)據(jù)量法，提高了計算時間序列LLE的精度，且通過適當(dāng)增加每次迭代的離散時間步長加快了計算LLE的速度.

1 預(yù)備知識

定義1.1Lyapunov指數(shù)：

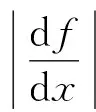
(1)

經(jīng)過n次迭代后，這兩點的距離變?yōu)?/p>

δxn=|fn(x0+δx0)-fn(x0)|.

(2)

定義LE如下[5-6]：

(3)

對于一般的n維動力系統(tǒng)，定義LE如下：設(shè)一個n維動力系統(tǒng)xn+1=F(xn)(Rn→Rn)，將系統(tǒng)的初始條件取為一個無窮小的n維小球，半徑取為ε(0)，由于演化過程中的自然變形，小球?qū)⒆兂蓹E球，見圖1.將橢球上所有主軸按照其長度排列，那么第i個LE根據(jù)第i個主軸的長度εi(t)的增加速率[7-8]定義為

(4)

最大的λi稱為LLE.系統(tǒng)的混沌狀態(tài)可以通過LLE的正負來判斷，當(dāng)LLE大于零時系統(tǒng)處于混沌狀態(tài)；當(dāng)LLE小于零時系統(tǒng)穩(wěn)定.

圖1 3維球面隨時間的演化

根據(jù)定義計算LE的方法稱為定義法，由于定義法計算LE時只適用于給定的系統(tǒng)，不能求時間序列[7-9]的LLE，因此Rosenstein提出了小數(shù)據(jù)量法.

定義1.2小數(shù)據(jù)量法：

對于時間序列{x1，x2，…，xN}的LLE可以用小數(shù)據(jù)量法，對于時間序列通過計算得[10]：設(shè)嵌入維數(shù)m，時間延遲為τ，平均周期為P，則重構(gòu)相空間為

Xi=[xi，xi+τ，…，xi+(m-1)τ]，i=1，2，…，M.

(5)

在重構(gòu)的相空間中尋找每個參考點Xj的最近鄰點Xj′，記

djj′(0)=min‖Xj-Xj′‖.

(6)

其中|j-j′|>P，P為時間序列的平均周期，可以通過基本軌道上每個點的平均發(fā)散速率計算.

對于每個參考點Xj，計算出其與最近鄰點Xj′的第i個離散時間步長后的距離djj′(i)為

djj′(i)=min‖Xj+i-Xj′+i‖，i=1，2，…，min(M-j，M-j′).

(7)

假定參考點Xj與最近鄰點Xj′的指數(shù)發(fā)散率為λ1，那么

djj′(i)=Cjeλ1(i·Δt)，Cj=djj′(0)，

(8)

上式兩邊取對數(shù)得

lndjj′(i)=lnCj+λ1(i·Δt).

(9)

由(9)式可以看出lndjj′(i)與變量i滿足線性關(guān)系，其曲線斜率為λ1Δt.

因此固定i，對所有的lndjj′(i)求平均再除以Δt，得到平均發(fā)散程度指數(shù)

(10)

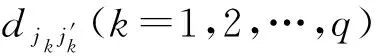
2 模糊C均值聚類小數(shù)據(jù)量法

2.1 模糊C均值聚類算法

在眾多模糊聚類算法中，模糊C-均值算法通過優(yōu)化目標(biāo)函數(shù)得到每個樣本點對所有類中心的隸屬度，從而決定樣本點的類屬以達到自動對樣本數(shù)據(jù)進行分類的目的.過程如下：

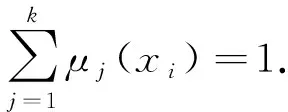
(11)

(12)

采用迭代的方法，通常情況下取初始隸屬度矩陣為每行為隨機單位向量的矩陣，b=2，最大迭代次數(shù)為100，隸屬度最小變化量為10-6，求解(11)和(12)式，直至滿足收斂條件，得到最優(yōu)解.

2.2 模糊C均值聚類算法選擇線性區(qū)域

在小數(shù)據(jù)量法計算LLE時將模糊C均值聚類算法用于選取線性區(qū)域，具體過程如下：

(1) 運用模糊C均值聚類算法將y(i)數(shù)據(jù)分為不飽和區(qū)域(y(i)達到基本穩(wěn)定之前)和飽和區(qū)域(y(i)在一條水平直線附近做微小波動)兩類，如圖2所示.

(2) 對于不飽和區(qū)域需要選出線性區(qū)域，用二階差分ddy(i)近似替代二階導(dǎo)數(shù)，對于不飽和區(qū)域的二階差分(i，ddy(i))將其分成3類，如圖3所示.結(jié)合不飽和區(qū)域平均發(fā)散程度指數(shù)的圖像與不飽和區(qū)域的二階差分的圖像可以看出，當(dāng)i較小時離散程度較大，當(dāng)i較大時線性化程度較低.因此將不飽和區(qū)域的y(i)-i分成3類，如圖4所示，選取第2類作為最終選擇的線性區(qū)域，其斜率就是LLE.

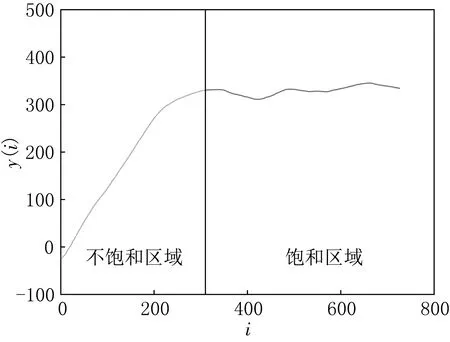
圖2 平均發(fā)散程度指數(shù)

圖3 不飽和區(qū)域平均發(fā)散程度指數(shù)二階差分分類

2.3 模糊C均值聚類小數(shù)據(jù)量法

對于時間序列{y1，y2，…，yN}，嵌入維數(shù)my，時間延遲為τy，平均周期為Py，則重構(gòu)相空間為

Yi=[yi，xi+τy，…，yi+(my-1)τy]，i=1，2，…，My.

(13)

在重構(gòu)的相空間中尋找每個參考點Yj的最近鄰點Yj′，有

Djj′(0)=min‖Yj-Yj′‖.

(14)

其中|j-j′|>Py，Py為時間序列的平均周期，可以通過基本軌道上每個點的平均發(fā)散速率計算.

對于每個參考點Yj，計算出其與最近鄰點Yj′的第ni(n=1，2，3，…)個離散時間步長后的距離為

Djj′(ni)=‖Yj+ni-Yj′+ni‖，

(15)

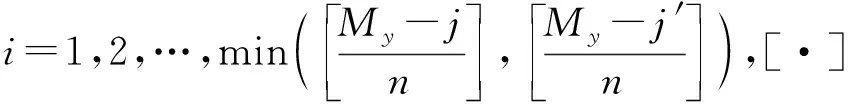
假定參考點Yj與最近鄰點Yj′的指數(shù)發(fā)散率為λ，那么

Djj′(ni)=Ajeλ(ni·Δt)，Aj=Djj′(0)，

(16)

上式兩邊取對數(shù)得

lnDjj′(ni)=lnAj+λ(ni·Δt).

(17)

由(17)式可以看出lnDjj′(ni)與i滿足線性關(guān)系，其曲線斜率為nλΔt.

因此固定i，對所有的lnDjj′(ni)求平均再除以Δt，得到平均發(fā)散程度指數(shù)

(18)

3 數(shù)值實驗

為了驗證模糊C均值聚類小數(shù)據(jù)量法的有效性，以典型的Lorenz系統(tǒng)[11]為例，選兩組不同的系數(shù)進行數(shù)值實驗.Lorenz系統(tǒng)為

(19)

取4個不同的初始點A1=[0.046 2，0.097 1，0.823 5]，A2=[0.694 8，0.317 1，0.950 2]，A3=[1，4，10]，A4=[0.119 0，0.498 4，0.959 7]，取a=16，b=4，c=45.92，此時LLE理論值為1.501 5.取積分步長為0.01，演化點3 000個，用小數(shù)據(jù)量法和模糊C均值聚類小數(shù)據(jù)量法(重構(gòu)維數(shù)為5，時間延遲為10，平均周期為40)計算LLE所得結(jié)果與誤差率見表1，小數(shù)據(jù)量法簡稱AL1，模糊C均值小數(shù)據(jù)量法簡稱AL2.

取4個不同的初始點A1=[0.046 2，0.097 1，0.823 5]，A2=[0.694 8，0.317 1，0.950 2]，A3=[1，4，10]，A4=[0.119 0，0.498 4，0.959 7]，取a=16，b=4，c=45.92，此時LLE理論值為1.501 5.取積分步長為0.01，演化點5 000個，用小數(shù)據(jù)量法和模糊C均值聚類小數(shù)據(jù)量法(重構(gòu)維數(shù)為5，時間延遲為10，平均周期為40)計算LLE所得結(jié)果與誤差率見表2.

取初始點A1=[0.046 2，0.097 1，0.823 5]，取a=16，b=4，c=45.92，此時LLE理論值為1.501 5.取積分步長為0.01，分別演化3 000個點與5 000個點，用模糊C均值聚類小數(shù)據(jù)量法(重構(gòu)維數(shù)為5，時間延遲為10，平均周期為40)每次分別演化i，2i，3i，4i(i的取值見上文)個離散時間步長，LLE計算結(jié)果與運行時間見表3.

取初始點A1=[0.046 2，0.097 1，0.823 5]，取a=10，b=8/3，c=28，此時LLE理論值為0.881 0.取積分步長為0.01，分別演化3 000個點與5 000個點，用模糊C均值聚類小數(shù)據(jù)量法(重構(gòu)維數(shù)為5，時間延遲為25，平均周期為40)每次分別演化i，2i，3i，4i(i的取值見上文)個離散時間步長，LLE計算結(jié)果與運行時間見表4.

從表1與表2結(jié)果可以看出，對比于小數(shù)據(jù)量法，文中提出的模糊C均值小數(shù)據(jù)量法計算LLE可以提高計算精度；從表3與表4結(jié)果可以看出，模糊C均值小數(shù)據(jù)量法計算LLE時隨著每次迭代的離散時間步長的增加，計算時間將縮短，但每次迭代的離散時間步長不宜過大.實驗結(jié)果驗證了算法是有效可行的.

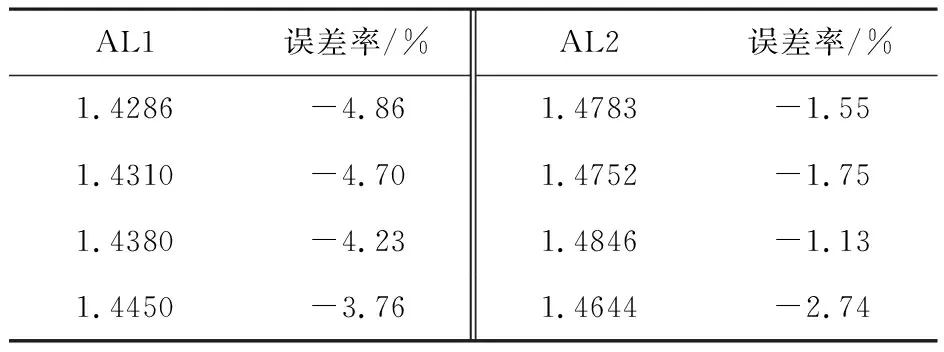
表1 3 000個演化點時小數(shù)據(jù)量法與模糊C均值小數(shù)據(jù)量算法的計算結(jié)果對比

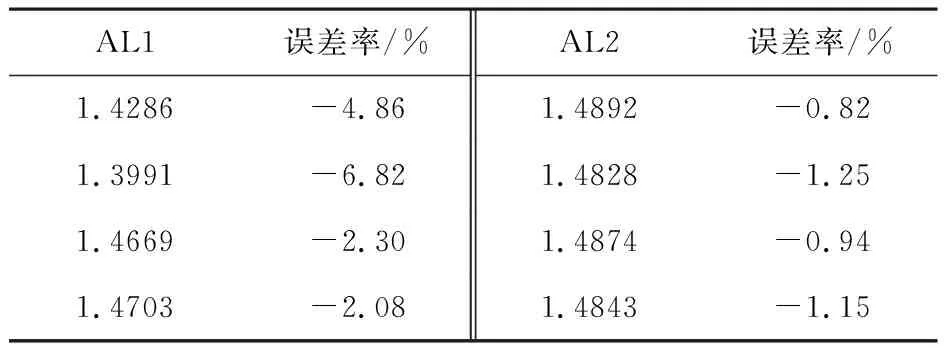
表2 5 000個演化點時小數(shù)據(jù)量法與模糊C均值小數(shù)據(jù)量法的計算結(jié)果對比

表3 模糊C均值小數(shù)據(jù)量法改變步長的計算結(jié)果1(LLE理論值為1.501 5)

表4 模糊C均值小數(shù)據(jù)量法改變步長的計算結(jié)果2(LLE理論值為0.881 0)

4 結(jié)論

將模糊C均值聚類算法用于小數(shù)據(jù)量法線性區(qū)域的選擇而提出的模糊C均值小數(shù)據(jù)量法來計算LLE，通過選出小數(shù)據(jù)量法的線性區(qū)域，可以大大提高小數(shù)據(jù)量法的計算精度.實驗表明，當(dāng)每次迭代的離散時間步長增加時，計算時間將減少.接下來可以研究離散步長的選取對于實驗精度和效率的影響，從而得到更為完善的模糊C均值小數(shù)據(jù)量法.