應用GM(1,1)模型預測甘孜州接待國內游客人次
趙江林

【摘要】本文根據甘孜州2008~2018年接待國內游客人次建立GM(1,1)灰色預測模型.對原始序列進行對數變換,可使GM(1,1)預測模型精度較高.2019~2021年甘孜州接待國內游客人次呈上升趨勢且增幅較大.則GM(1,1)模型可用于甘孜州接待國內游客人次的短中期預測.預測結果對甘孜州旅游發展具有一定的參考意義.
【關鍵詞】接待國內游客人次;GM(1,1)模型;預測;甘孜州
1 引言
甘孜藏族自治州(簡稱甘孜州)旅游自然資源豐富,每年吸引大量國內游客前往,特別是自2017年雅康高速開通以后,進藏的時間大大縮短了,游客大量增加.甘孜州以瑰麗的高原地理地貌和獨特的藏民族文化和生活令無數游客向往.因此,預測甘孜州旅游游客數量能夠為旅游行業從業者和旅游政策制定者提供參考,提升甘孜旅游品牌形象,助推少數民族地區發展.
灰色預測模型基于數據本身,能夠減少時間序列的隨機性,具有所需樣本量小、計算簡便、預測效果較好等優點. GM(1,1)模型是灰色預測模型中最廣泛使用的模型.當前GM(1,1)模型已被廣泛應用在傳染病、經濟、農業、工程、體育等方面的預測.本文根據甘孜州2008~2018年接待國內游客人次建立GM(1,1)灰色預測模型,對甘孜州2019~2021年接待國內游客人次進行預測,為甘孜州旅游業的進一步發展提供參考.
2 資料與方法
2.1 資料
2008年至2018年四川省甘孜藏族自治州接待國內游客人次數據來源于甘孜州的歷年國民經濟和社會發展統計公報.
2.2 方法
2.2.1 GM(1,1)模型的建立
GM(1,1)模型是通過將離散隨機的原始時間序列累加生成為隨機性被顯著削弱且較有規律的序列,建立相應的微分方程動態模型,然后利用該微分方程進行預測.下面我們建立灰色預測GM(1,1)模型.
2.2.2 模型檢驗
設原始序列為x(0),GM(1,1)模型的預測序列為x^(0),則x(0)的均值為x-=1n∑nk=1x(0)(k),x(0)的方差為s2x=1n-1∑nk=1x(0)(k)-x-2.設原始序列與預測序列的殘差為ε,則殘差的均值為ε-=1n∑nk=1ε(k),殘差的方差為s2ε=1n-1∑nk=1ε(k)-ε-2.因此殘差與原始序列的均方差比值為C=sεsx,小殘差概率為P=Pε(k)-ε-<0.6745sx.若對于給定的均方差比值C0>0,當C
3 結果
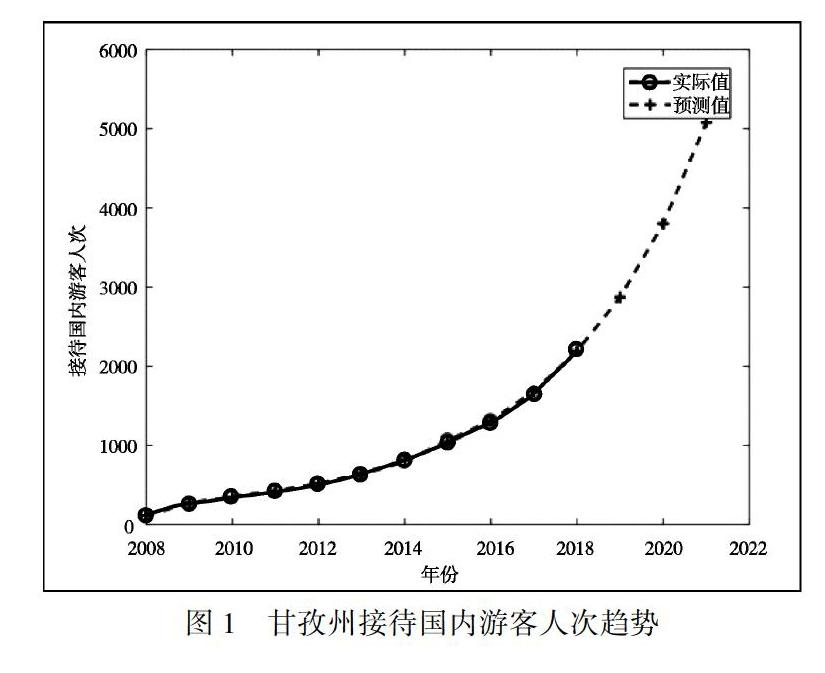
2008~2018年甘孜州接待國內游客人次原始時間序列為x(0),如果直接采用GM(1,1)模型預測,則相對誤差序列中最大相對誤差為14.2%,最小相對誤差為0.1%,平均相對誤差為5.3%,相對誤差一致性較差.因此,為了提高相對誤差的一致性和精度,我們對原始序列取自然對數得到y(0)=log(x(0)),對新的序列y(0)應用GM(1,1)模型得到預測序列y^(0),再對預測序列y^(0)進行還原運算得到原始序列x(0)的預測序列x^(0)=expy^(0)(如表2所示).如表2所示,采用對數變換后應用GM(1,1)模型,相對誤差序列中,最大誤差為4.5%,最小誤差為0.2%,平均誤差為2.2%.故對甘孜州接待國內游客人次原始時間序列應用對數變換后的GM(1,1)模型提高了預測精度.
經擬合優度檢驗均方差比值C=0.037,小殘差概率P=1,模型預測等級為1級(優).因此該模型可以用于外推預測短期甘孜州接待國內游客人次(如圖1所示).假設不發生重大影響人們旅行計劃的事件,我們用該模型預測甘孜州2019~2021年接待國內游客人次分別為2872.3萬人次、3800.8萬人次、5079.3萬人次,總體呈上升趨勢.
4 討論
灰色預測模型是一種全因子的非線性擬合外推類方法模型.我們將甘孜州的發展變遷當作一個灰色系統,用灰色模型去發展,認識其原始時間數據序列中蘊含的內在規律,從而預測接待國內游客的發展趨勢.由于甘孜州接待國內游客人次遠遠超過接待境外游客人次,則我們可以將甘孜州接待國內游客人次視為甘孜州接待游客人次.因此,本文數值模擬只考慮甘孜州接待國內游客人次而不考慮接待境外游客人次.由模型預測可以看出,甘孜州接待國內游客人次將保持較高增長的態勢,尤其是自2017年過后增長速率明顯加快.這是在提醒我們,游客人數在持續增長的情況下,旅游服務業要能夠跟上.因此,該模型預測為甘孜州旅游行業和相關職能部門提供了一定的科學決策和參考意義.另一方面,灰色預測模型只能反映數據的內在規律性,不能反饋各種自然事件、社會因素對數據的影響.因此,在制定旅游發展規劃和相關政策時,旅游行業和相關職能部門還應該具體考慮當地的自然、社會、環境對其的影響.
【參考文獻】[1]馬霞,陳娜,刑青紅,原錦濤.灰色模型在新疆地區包蟲病流行預測中的應用[J].周口師范學院學報,2019,36(5):26-30.
[2]安曉紅.灰色系統GM(1,1)模型在預測徐州市甲乙類呼吸道傳染病發病趨勢中的應用[J].江蘇預防醫學,2019,30(1):33-35.
[3]官金蘭,賴煜庭.基于灰色系統的房價分析與預測模型[J].清遠職業技術學院學報,2019,12(2):31-34.
[4]劉柏陽,劉立剛.灰色預測模型在區域物流成本中的應用研究[J].會計之友,2018(23):23-26.
[5]季宇.組合灰色模型在黑土區玉米產量預測中的應用[D].長春:吉林農業大學,2018.
[6]李志勇,張成.四川省入境旅游客流量預測研究:基于灰色預測模型[J].赤峰學院學報(自然科學版),2014(22):97-99.
[7]楊飛,張瑩.吉林省入境旅游客源灰色預測模型[J].吉林工商學院學報,2012(3):20-23.
[8]徐鴻,鄧博,蔣東方,郭鵬,倪永中.基于灰色系統的過熱器管壁溫度預測模型[J].中國機械工程,2017,28(22):2662-2668.
[9]劉忠賀,李宗春,何華,郭迎鋼.灰色系統及線性回歸模型在變形沉降中的應用[J].測繪通報,2018(S1):262-265.
[10]胡承洪,程林林,張永韜.體育產業結構灰色評價模型與結構優化戰略的探討:以四川省為例[J].成都體育學院學報,2012,38(6):1-8.

