以“不變”應“萬變”
——2020年全國Ⅰ卷的兩道動態(tài)類題
何彥雨 李富恩 陳 菁
(1. 北京林業(yè)大學理學院,北京 100083; 2. 澳門城市大學教育學院,澳門 999078;3. 華北油田第三中學,河北 任丘 062552)
1 原題呈現(xiàn)
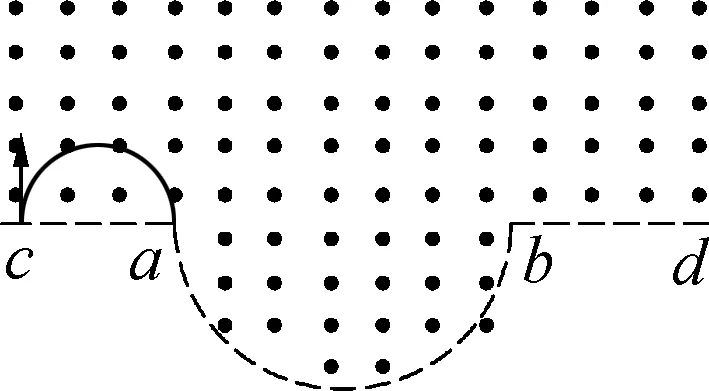
圖1 2020年全國Ⅰ卷18題圖


答案: (C).
2 動態(tài)圖解法探析
粒子僅受洛倫茲力,在磁場中做勻速圓周運動,
可得粒子在磁場中運動的周期為
設粒子在磁場中運動的時間為t,則有
則對于給定的粒子在磁場中運動的時間與速度無關,僅由圓心角決定,軌跡對應的圓心角θ越大,運動的時間就越長.筆者通過改變圓的半徑來解決該問題,粒子垂直ac射入磁場,軌跡圓心必在ac這條直線上,現(xiàn)將粒子的軌跡半徑由0逐漸放大分別進行討論.
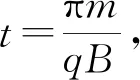

(a)
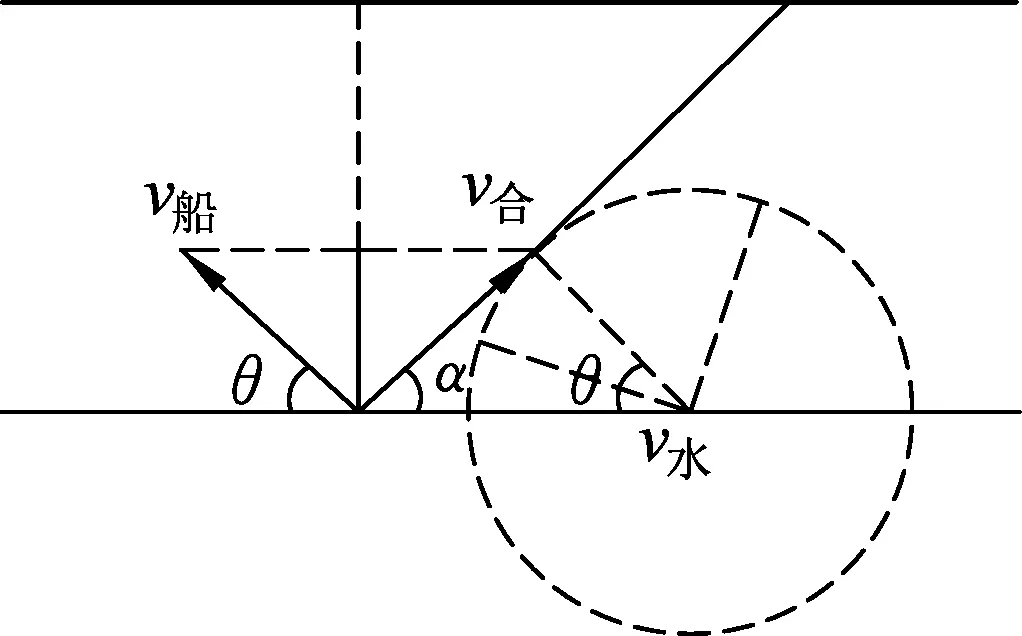
當0.5R 粒子運動最長時間為 故選(C). 圖3 當0.5R 另外,在解答本題時如果沒有考慮到“動態(tài)圖”的幾何解題方法,那么采用較為常規(guī)的代數(shù)方法來求解函數(shù)極值的亦可,利用余弦定理來求得此題目中函數(shù)極值確定時間最長時的軌跡圓心位置. 圖4 運動軌跡各邊角示意圖 如圖4所示,由余弦定理可得 R2=r2+(2R-r)2-2r(2R-r)cosθ. 化簡可得 所以,當r=R時上列式子有最小值,即θ有最大值.因此當軌跡半徑等于R時軌跡圓心角最大. 圖5 2020年全國Ⅰ卷25題圖 (2020年全國Ⅰ卷第25題)在一柱形區(qū)域內(nèi)有勻強電場,柱的橫截面積是以O為圓心,半徑為R的圓,AB為圓的直徑,如圖5所示.質(zhì)量為m,電荷量為q(q>0)的帶電粒子在紙面內(nèi)自A點先后以不同的速度進入電場,速度方向與電場的方向垂直.已知剛進入電場時速度為0的粒子,自圓周上的C點以速率v0穿出電場,AC與AB的夾角θ=60°.運動中粒子僅受電場力作用.求: (1) 求電場強度的大小; (2) 為使粒子穿過電場后的動能增量最大,該粒子進入電場時的速度應為多大? 注:由于本題第(3)問不涉及動態(tài)問題,所以暫不展示. (1) 由題意知粒子在A點速度為0,它將會沿著電場線方向運動,因為q>0,故電場線的方向由A指向C,由題中條件分析可知 xAC=R. 由動能定理 解得 圖6 動態(tài)圖解法粒子運動軌跡示意圖 (2) 由題意可知,粒子動能增量最大,則它必然沿電場線方向移動距離最多,粒子的初速度與電場線垂直,則它將做類平拋運動,以拋出點為原點,初速度的方向為x軸正方向,電場線方向為y軸正方向建立如圖所示坐標系,任找一條運動軌跡(初速度較大),與圓周交于一點E,通過E做x、y軸的平行線,與y軸的交點為F,則AF即為沿著電場力方向發(fā)生的位移,逐漸減小初速度,則F點將下移,同時AF也將增大,當EF剛好與圓周相切時,沿電場力方向發(fā)生的位移是最大的,繼續(xù)減小初速度,此位移將開始將小,所以E1F1與圓相切時射出時沿電場線方向移動距離最多,在此圖中,切點即為E1點, 根據(jù)類平拋運動,結(jié)合幾何關系有 x=Rsin60°=v1t, 根據(jù)牛頓第二定律有qE=ma. 聯(lián)立解得粒子剛進入電場時的速度 動態(tài)圖解決高中物理問題可應用于很多情境中,例如在高中物理經(jīng)典的“小船過河”題目中,就可以應用“動態(tài)圖”解法進行解決.讓我們來看下面這個題目. 已知一條小河的水流速度為v水,小河的寬度為L,船在靜水中的航行速度為v2,當v2小于v1時,小船應該如何行駛,才能使得小船的航行路程最短? 圖7 “小船過河”各物理量示意圖 若v船 無論是力學部分的題目,還是電學部分的題目,解決動態(tài)物理問題的思路都應該是緊密加深對理論知識的理解,教材中的知識和定義是考生解決高中物理動態(tài)問題的有效途徑.從上述題目中可以看出運用幾何圖形進行表述、分析物理問題是高考考查的一個既定方向.[1]例如上述2020年全國Ⅰ卷中的第18題,整體思路就是運用動態(tài)圖的解題方法,找出相關臨界狀態(tài),從而使問題得到解決.在高考復習中,我們必須加強對教材中相關重要圖像的教學,加強學生數(shù)形結(jié)合意識的培養(yǎng),全面提升學生作圖、識圖的能力,從而培養(yǎng)學生的發(fā)散思維、樹立良好的數(shù)理思想、建立物理模型,促進學生對問題情境有更加深入的理解,對物理過程有更加透徹的分析,達到培養(yǎng)學生高階思維的能力和發(fā)展學生核心素養(yǎng)的目標.[2-4]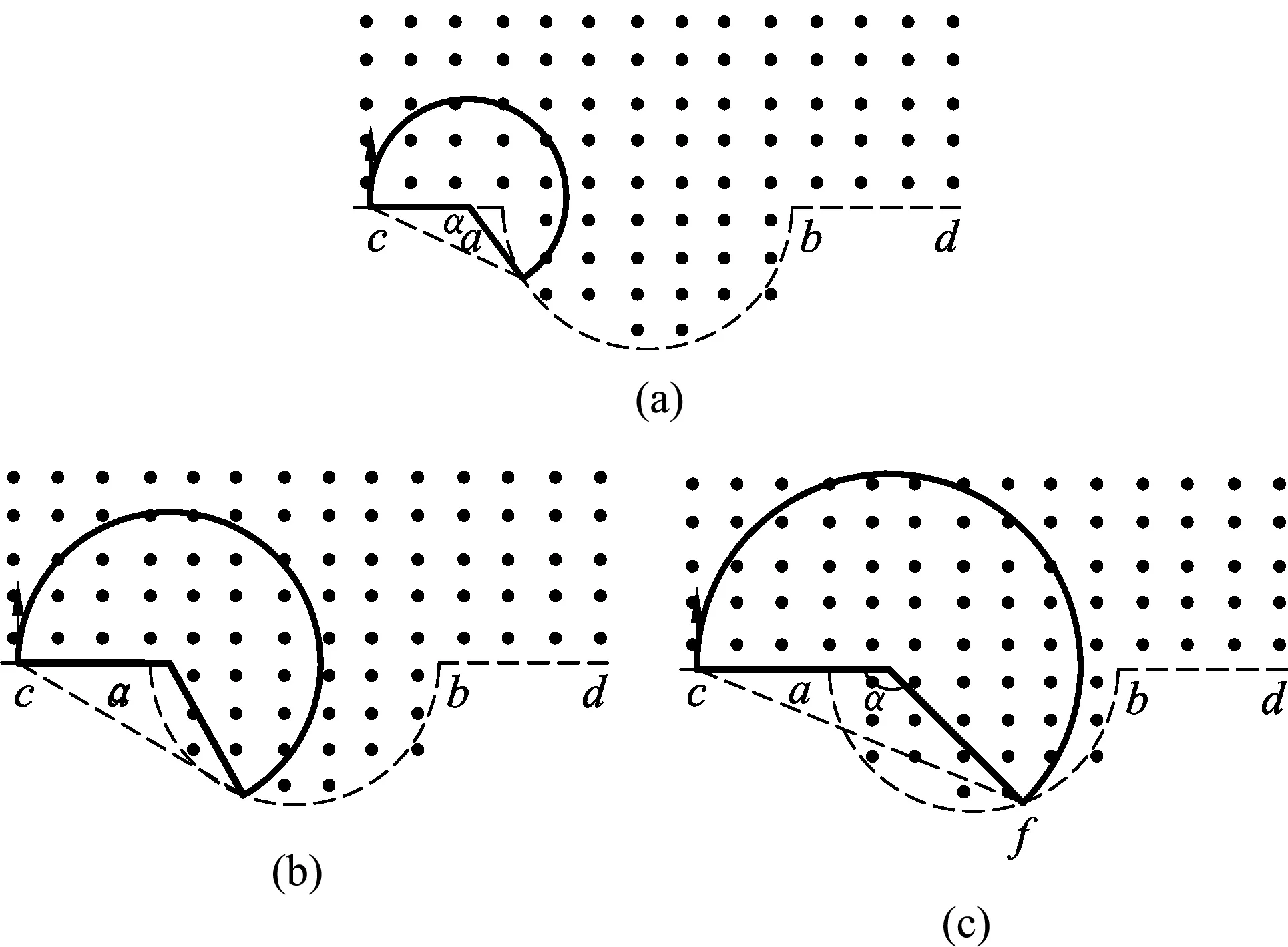

3 原題呈現(xiàn)


4 動態(tài)圖解法探析

5 題型拓展


6 結(jié)語

