矩形鋼箱梁鐵路斜拉橋渦振性能及氣動控制措施研究

黃 林，董佳慧，王 騎，李志國，高 貴，李世文

(1.西南交通大學 風工程試驗研究中心，成都 610031；2.風工程四川省重點實驗室，成都 610031；3.武九鐵路客運專線湖北有限責任公司，武漢 430201；4.中鐵大橋勘察設計院有限公司，武漢 430050)

隨著經濟和社會的發展，在世界范圍內，人們對大跨度鐵路橋梁的需求也日漸增長。由于剛度上的更高要求，跨越大江大河的鐵路橋多以斜拉橋為主，而其主梁形式也多采用鋼桁架梁。以往普遍采用的鋼箱梁，其體積質量更大，建造和維護成本也更高，因此開發適合鐵路用的鋼箱梁斜拉橋具備很大的市場前景。由于扁平鋼箱梁相對于桁架梁，其豎、橫向以及扭轉剛度均較小，無法滿足大跨度鐵路斜拉橋的設計要求，為了保證主梁剛度，在采用箱梁作為主梁截面時，就需要增大其腹板傾角以及增大梁高，這使最終滿足剛度要求的箱形斷面成為了寬高比較小(寬高比在7以下)的矩形斷面。大量的研究表明[1-5]，對于大部分外形具有典型鈍體特征的結構，例如矩形鋼箱梁，當氣流流經這些鈍體結構時，流動會產生分離和剪切層，出現漩渦的產生、合并和脫落現象，剪切層的再附以及與尾跡的相互作用將形成復雜的繞流形態，并產生周期性的非定常氣動力。因此當矩形斷面應用在柔性結構上時，會導致結構出現渦激振動現象。大跨度斜拉橋是柔性體系橋梁，因此當其主梁斷面為矩形時，也會發生渦激振動現象[6]。

渦激振動是一種帶有自激性質的限幅振動。當來流流經結構并發生分離后，會產生交替性的漩渦脫落，從而對結構產生周期性的渦激力，當其頻率與結構模態頻率接近時，就會引起渦激共振現象。渦激振動現象是大跨度橋梁在低風速下出現的一種風致振動現象，丹麥大貝爾特東橋[7]與中國西堠門大橋等[8]均出現過渦振現象。盡管渦激振動不會像顫振一樣帶來災難性的發散振動，但其發生在常遇低風速范圍，出現頻率較高，振幅較大，除了影響正常交通外，還可能導致構件的疲勞損傷。2020年，我國已建成的武漢鸚鵡洲長江大橋和廣東虎門大橋也發生了渦激振動現象，嚴重影響了正常交通，也對輿情有不利的影響。對于鐵路橋，渦激振動會嚴重影響列車的行駛安全，尤其是高速鐵路的行車安全，在設計中需要堅決避免。

針對如何改善鋼箱梁渦振性能這個主題，國內外學者已開展了相關研究，并提出了一些切實有效的氣動措施。Larsen等[9]對香港昂船洲橋主橋斷面進行不同尺度的節段模型風洞對比試驗，研究了該橋的氣動性能，并針對導流板的抑振機理進行討論。Nagao等[10]的研究表明，護欄的類型及位置對鋼箱梁主梁的渦激共振有顯著影響。李永樂等[11-12]提出了一種風嘴措施，可較好地抑制分離式雙箱梁的豎彎渦振以及扭轉渦振，同時也發現改變人行道護欄類型與導流板放置位置對扁平鋼箱梁的渦振性能有著明顯的影響。Wang等[13]發現15°斜腹板傾角可以顯著提高流線型箱梁的顫振和渦振性能。李明等[14]通過1∶50及1∶27節段模型風洞試驗研究了風嘴、檢修車軌道、導流板、抑振板和檢修道欄桿對寬幅流線型箱梁渦振性能的影響。孟曉亮等[15]通過風洞試驗發現較尖的風嘴角度可以有效提高全封閉鋼箱梁的渦振性能。日本抗風設計規范里，也列舉了多種抑制不同形式鋼箱梁渦振的措施。

目前，已有的文獻都是針對扁平箱梁或帶挑臂的梯形箱梁渦激振動所提出的制振措施，但幾乎沒有關于矩形鋼箱梁鐵路橋渦振制振研究的報道。同時，由于鐵路行車還需要有軌道板、軌道以及中央防拋網等措施，這些構件均會降低主梁的渦振性能[16-17]，因此相比較于簡單的幾何矩形斷面，實際中加裝了各種橋梁附屬構件的橋梁主梁斷面的渦振性能會出現一定程度上的降低。為了保障大跨度鐵路斜拉橋的行車安全，需要有效抑制矩形鋼箱梁主梁的渦激振動，并提出一種簡便適用的制振措施。

本文以某主跨為672 m的矩形鋼箱梁鐵路斜拉橋為工程背景，在借鑒已有研究成果的基礎上，分別采用1∶50及1∶25節段模型風洞試驗，研究了矩形斷面主梁的渦激共振及制振措施。在對比了裙板、導流板、欄桿透風率以及風嘴等氣動措施的制振效果基礎上，提出了一種帶平臺的三角形下行風嘴的制振措施，利用計算流體動力學(computational fluid dynamics，CFD)方法研究了主梁渦振的發生機理與帶平臺三角形下行風嘴的制振機理。

1 主梁渦振性能及氣動措施研究

1.1 試驗參數

斜拉橋主梁采用矩形閉口鋼箱梁，主梁高4.8 m，全寬32.2 m，寬高比6.71，其上布置有四線鐵路(兩線高鐵和兩線普鐵)，以及檢修道、軌道板、管線槽等附屬設施。由于高鐵行車安全的需要，在普速線路和高速線路之間增設了防拋網，位置在主梁上表面的中間位置，高度為3 m，透風率為65%，具體如圖1所示。

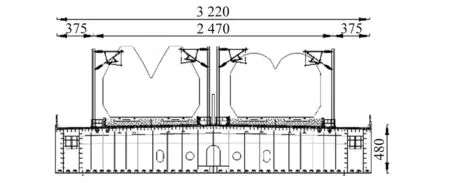
圖1 原始主梁斷面示意圖(cm)Fig.1 Cross section of prototype deck model (cm)

根據上述主梁斷面尺寸、試驗段尺寸以及試驗相關要求，在滿足幾何外形相似、彈性參數相似、慣性參數相似以及阻尼參數相似的情況下，選取試驗模型縮尺比為1∶50，模型長度L=2.095 m，寬度B=0.644 m，高度H=0.096 m。節段模型外衣內部采用木質框架，外表采用木板蒙皮制成，軌道板、欄桿、中央防拋網以及梁底的檢修車軌道采用ABS塑料板制作并確保外形及透風率相似，試驗中采用激光位移傳感器測量并記錄主梁位移響應，兩個傳感器固定在節段模型下部一定高度處，用以采集試驗過程中節段模型的位移數據。采用彈簧懸掛的方式安裝模型，如圖2所示。渦振試驗在西南交通大學XNJD-1風洞第二試驗段進行，該試驗段截面尺寸為2.4 m×2.0 m，風速范圍為1.0～45.0 m/s。

圖2 彈簧懸掛節段模型Fig.2 Spring-suspended sectional model

由于目前尚沒有針對大跨度鋼箱梁鐵路橋風洞試驗阻尼比取值的相關規定，參考陳平等[18]針對鐵路橋開展的風洞試驗的阻尼比取值，本次試驗中，豎彎阻尼比取值為0.52%，扭轉阻尼比取值為0.49%。

對于鐵路橋梁的渦振限制，目前國內外還沒有相關規范條文出臺，因此本文對渦振振幅的評判參考了以下規范：我國發布的TB 10621—2014《高速鐵路設計規范》[19]中關于主梁豎彎和扭轉振幅限值、JTG/T 3360-01—2018《公路橋梁抗風設計規范》[20]、英國發布的BD 49/01《Design rules for aerodynamic effects on bridges》[21](以下簡稱英規)的加速度限值以及日本《Wind resistant design manual for highway bridges in Japan》[22](以下簡稱日本指南)，采用四種規范計算得到本文中鐵路橋渦振振幅的限值，如表1所示。從表1中可以看出，日本指南對于豎彎渦振振幅限值的取值相對更加嚴格，因此參考該規范計算豎彎渦振振幅限值是偏于安全的。

表1 各國規范渦振振幅限值Tab.1 The allowable value of VIV displacement in various countries

實際上，若鐵路橋梁發生渦振，其變換的振幅對鐵路行車影響是動態的，此時振幅的限值會比通過靜態轉角確定的限值要小，因此，在這里取四種規范計算得到的渦振振幅限值的最小值。

大跨度橋梁的豎向渦振通常表現為單一模態的振動，但大跨度橋梁模態密集，在橋梁正常運營風速限值25 m/s內，固有頻率在0.6 Hz以內的豎彎模態都有發生渦振的可能[23]。考慮到實際橋梁中主梁的扭轉頻率要比豎彎頻率高，橋梁在常遇風速下發生高階扭轉渦振的可能性較小[24]，表2列舉了前5階豎彎模態的渦振振幅限值以供參考。

表2 前5階豎彎模態渦振振幅限值Tab.2 The first five allowable value of vertical VIV displacement

由于第1階模態對應的渦振風速最低，因此在節段模型渦振試驗的相關參數中，模態頻率選擇了豎向和扭轉振動的基頻，具體如表3所示。并取豎彎渦振振幅限值為142 mm，扭轉渦振振幅限值為0.179°。

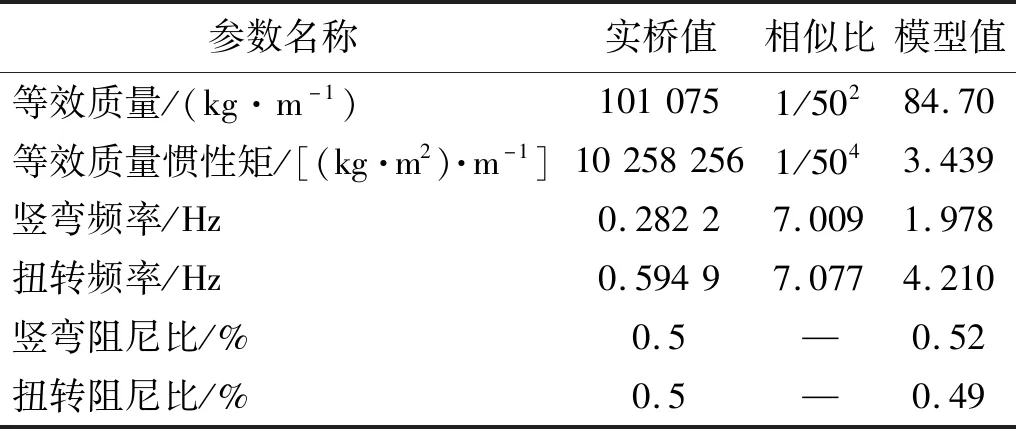
表3 1∶50節段模型試驗動力參數Tab.3 Dynamic parameters of 1∶50 section model tests

1.2 原設計矩形斷面的渦振性能

渦激振動試驗在均勻流場中進行，風洞中的風速范圍為0.5～6.0 m/s(實橋風速范圍為3.5～42.0 m/s)，風洞中風速間隔為0.15 m/s(實橋風速間隔約為1.00 m/s)。分別在0°，±3°，±5°攻角下測試了主梁豎彎及扭轉渦振，如圖3所示 (圖中風速和振幅數據均已換算成實橋)。

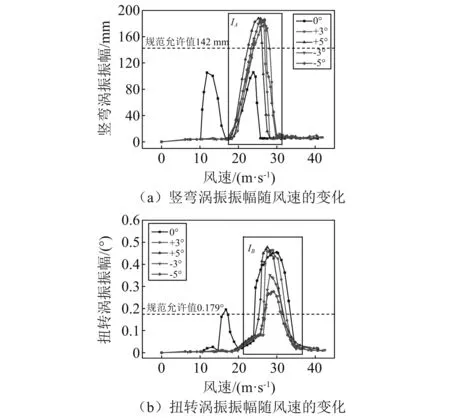
圖3 原設計矩形斷面主梁渦振振幅(縮尺比1∶50)Fig.3 VIV displacement of the main girder with original deck (scale ratio:1∶50)

(1) 在0°風攻角下，原設計矩形斷面存在兩個豎彎渦振區間與兩個扭轉渦振區間，其中兩個豎彎渦振區間的振幅均沒有超過限值，但高風速下扭轉渦振區間IB內的扭轉渦振振幅最大超過渦振限值1.54倍；

(2) 在±3°，±5°風攻角下，存在一個高風速下豎彎渦振區間IA(20.0～25.0 m/s風速下)與一個高風速下扭轉渦振區間IB(26.0～33.0 m/s風速下)，且振幅均顯著超過限值，其中豎彎渦振振幅最大超過渦振限值32.29%，扭轉渦振振幅最大超過渦振限值1.67倍。

因此，為保障橋梁運營期間鐵路行車的安全性，需要對主梁的渦振性能進行優化，提出合理有效、簡便易行的制振措施。

1.3 主梁渦振制振措施研究

主梁斷面的氣動外形對其渦振性能有著重要影響，參考已有的研究成果[25-27]，本文采用設置裙板、導流板、風嘴以及改變外側人行道欄桿透風率這幾種氣動措施，如表4所示。測試了不同工況下主梁渦振的振幅。試驗重點考察了風嘴(實際長度均為4 m)的渦振控制效果，其中，風嘴尖角位于對稱線以上的稱為上行風嘴，風嘴尖角位于對稱線以下的稱為下行風嘴，風嘴尖角位于對稱線的稱為對稱風嘴，如圖4所示。試驗中分別選取了三角形上行風嘴(風嘴Ⅰ)，三角形對稱風嘴(風嘴Ⅱ)以及三角形下行風嘴(風嘴Ⅲ)。

表4 節段模型渦振制振氣動措施示意圖Tab.4 Aerodynamic measures and structural details cm

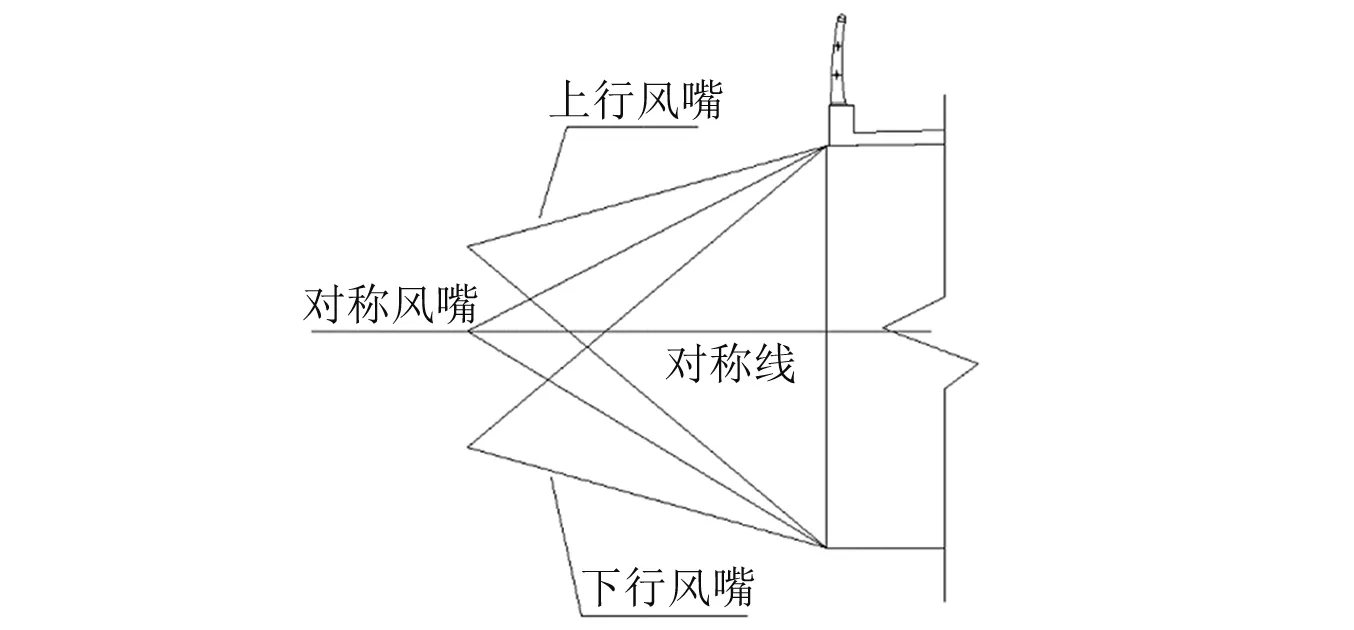
圖4 風嘴分類示意圖Fig.4 Diagram of wind fairing classification

通過對原設計矩形斷面的渦振性能試驗結果可知，該主梁在各風攻角下均發生了渦激振動。考慮到其代表性和特殊性，在考察制振措施的風洞試驗中，選取0°風攻角和振幅最大時對應的+5°風攻角開展相關測試。各種氣動措施對應的最大渦振振幅如圖5與圖6所示(圖中數據均已換算成實橋)。

由圖5與圖6可知，在六種氣動措施中，除了將外側人行道欄桿進行間隔封閉的措施無效外(該氣動措施甚至還會增大主梁渦振振幅)。在裙板、導流板和風嘴這三種措施的測試結果中，主梁的豎彎最大渦振振幅均低于規范限值，說明這幾種氣動措施起到了一定的制振作用。其中：在0°風攻角下三角形風嘴均能將主梁豎彎最大渦振振幅降低87%以上(降低率以原設計矩形斷面相對應工況為基準計算)；在+5°風攻角下三角形風嘴均能將主梁豎彎最大渦振振幅降低56%以上，三角形風嘴對于主梁豎彎渦振的制振能力明顯優于裙板與導流板。

圖5 各工況最大豎彎渦振幅值Fig.5 Vertical maximum VIV displacement of each working condition

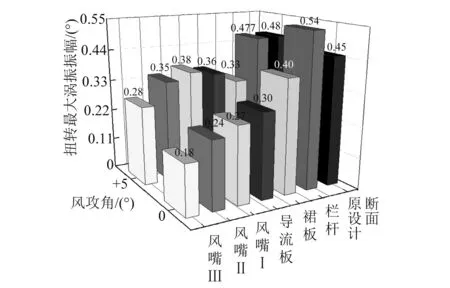
圖6 各工況最大扭轉渦振幅值Fig.6 Torsional maximum VIV displacement of each working condition

如圖6所示，風嘴Ⅰ、風嘴Ⅱ與風嘴Ⅲ三種風嘴對于主梁扭轉最大渦振振幅的降低率依次分別為20.83%，27.08%與41.67%，三種風嘴對主梁渦振制振能力排序為風嘴Ⅲ>風嘴Ⅱ>風嘴Ⅰ，即下行風嘴效果更佳。但其他措施對扭轉渦振的抑制效果均較差。

2 帶平臺的三角形風嘴制振措施研究

通過風洞試驗結果可知，三角形風嘴作為一種氣動措施可以有效地抑制主梁的豎彎渦振，但對于抑制主梁扭轉渦振的效果不佳。綜合之前所得到的下行風嘴制振能力較好的結論，在三角形下行風嘴上部設置一個實際長度為75 cm的平臺(改變氣流在梁體上部的分離點)，提出了一種帶平臺的三角形下行風嘴(風嘴Ⅳ)，措施具體細節如圖7所示。

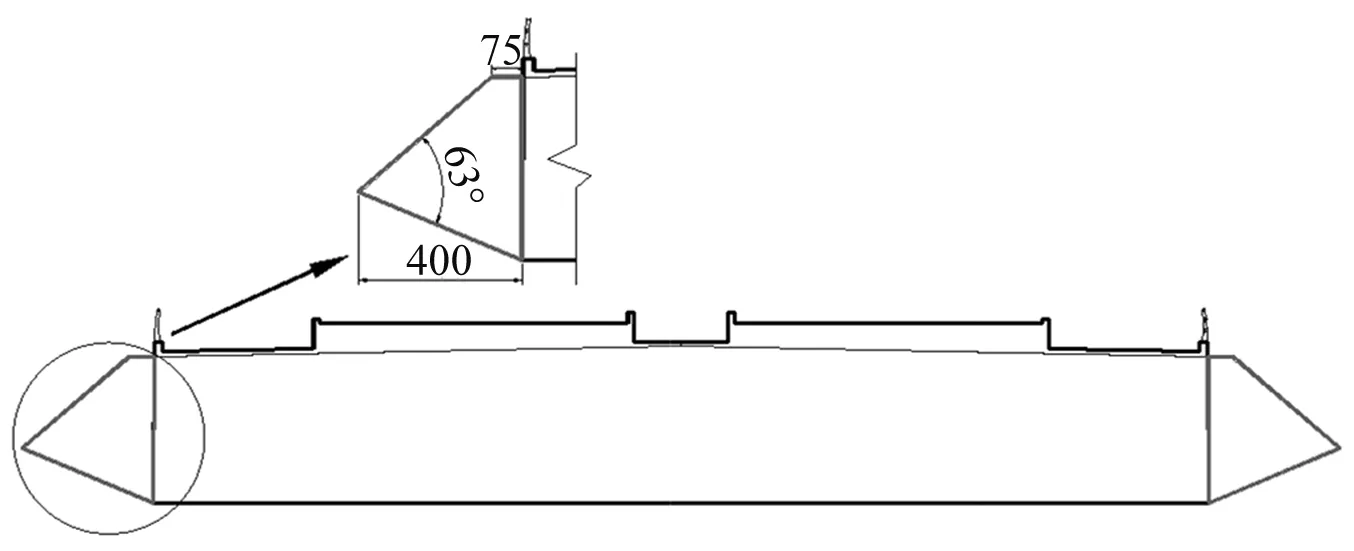
圖7 風嘴Ⅳ示意圖(cm)Fig.7 Diagram of wind fairing Ⅳ (cm)

對加裝了風嘴Ⅳ的主梁進行1∶50節段模型渦振試驗，在0°，±3°，±5°攻角和0.5%阻尼比下，主梁豎彎及扭轉渦振振幅，如圖8所示(圖中數據均已換算成實橋)。

由圖8(a)可知，加裝風嘴Ⅳ后，主梁的豎彎渦激振動得到了顯著抑制，僅在+5°風攻角下發生明顯豎彎渦激振動，風速區間為10.0～15.0 m/s，且最大振幅值為40 mm，遠遠小于渦振振幅限值，在+3°風攻角下發生輕微豎彎渦激振動，最大振幅值僅為12 mm。在其余風攻角下，主梁的豎彎渦激振動均被完全消除。

由圖8(b)可知，加裝風嘴Ⅳ后，主梁的扭轉渦激振動得到了極大的抑制，主梁僅在+5°與+3°風攻角下發生扭轉渦激振動，風速區間為20.0 ～28.0 m/s，最大振動幅值分別為0.046°與0.033°，均遠小于渦振振幅限值。在其余風攻角下，扭轉渦激振動幾乎消失。

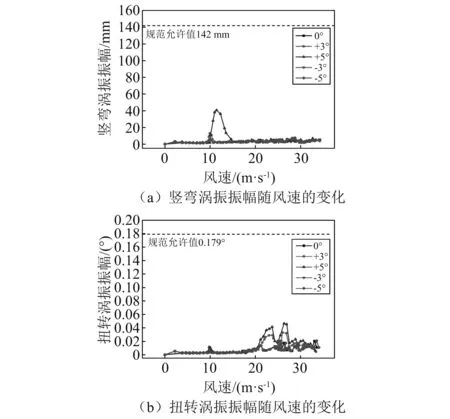
圖8 工況風嘴Ⅳ斷面主梁渦振振幅(縮尺比1∶50)Fig.8 VIV displacement of the main girder with case wind fairing Ⅳ (scale ratio:1∶50)

通過1∶50節段模型風洞試驗，可以發現風嘴Ⅳ作為一種帶平臺的三角形下行風嘴對主梁渦振的抑制效果十分顯著，滿足相應的渦振振幅規范要求。需要說明的是，采用此風嘴后，在沒有中間防拋網的條件下，主梁的豎向和扭轉渦振在不同攻角下都可以完全消除。

此外，通過風洞試驗還發現，平臺的長度對渦振的制振效果也有一定的影響，以平臺長度為75 cm的風嘴Ⅳ為基礎，在僅改變風嘴平臺長度的情況下，主梁在0°與+5°風攻角下的最大渦振振幅，如表5所示。當平臺長度為50 cm時，主梁渦振較大，制振效果不好，最大扭轉渦振振幅超過限值。當平臺長度為100 cm時，主梁的扭轉渦振振幅雖然低于限值，但是大于平臺長度為75 cm時的值，因此在不改變風嘴總長度的情況下，平臺長度過大或者過小都會影響風嘴的制振效果。

表5 不同平臺長度風嘴下渦振振幅Tab.5 VIV displacement under wind fairing with different platform lengths

3 大比例尺節段模型渦振試驗

由于常規尺度(1∶50)節段模型尺寸較小，對橋梁結構模擬不夠精細，加上風速比大，從而導致對實橋渦振性能的評估存在一定偏差[28]。采用大尺度主梁節段模型(通常為1∶15～1∶30)進行風洞試驗是克服上述弊端的有效方法之一[29-30]。為此，有必要開展大比例尺節段模型渦振風洞試驗，進一步驗證風嘴Ⅳ對主梁渦激振動的制振效果。

加裝了風嘴Ⅳ的主梁大尺度節段模型風洞試驗縮尺比為1∶25，試驗在XNJD-3大氣邊界層風洞中(試驗斷面寬22.5 m，高4.5 m)的專用裝置上進行，風洞試驗照片如圖9所示。節段模型的主要試驗參數，如表6所示。試驗風速比為1.00∶4.45，在來流風攻角分別為0°，±3°，±5°的均勻流下進行，結構阻尼比為0.47%。

圖9 1∶25節段模型風洞布置圖Fig.9 Layout of the 1∶25 section model wind tunnel test

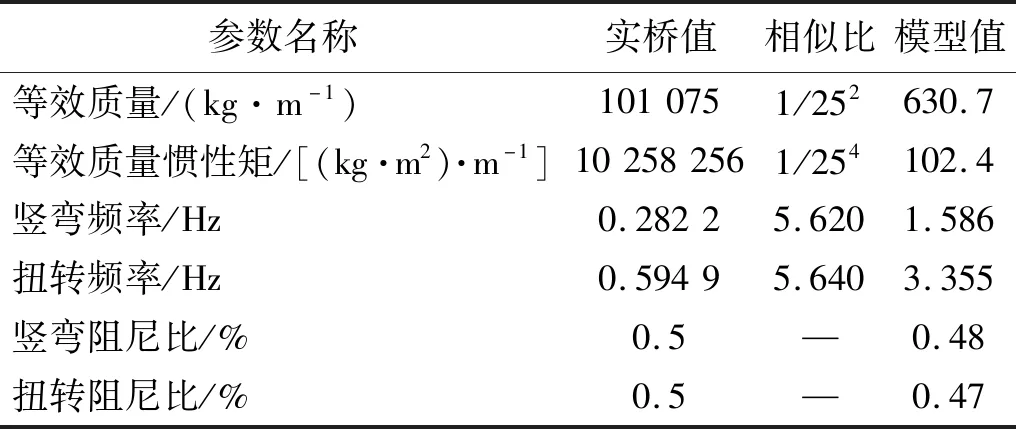
表6 1∶25節段模型試驗動力參數Tab.6 Dynamic parameters of 1∶25 section model tests

圖10為加裝了風嘴Ⅳ后主梁渦激振動響應隨風速的變化曲線，風致響應及風速均已換算至實橋值。

由圖10(a)可知，加裝風嘴Ⅳ后，通過1∶25節段模型風洞試驗得到的主梁豎彎渦激振動結果與通過1∶50節段模型風洞試驗得到的主梁豎彎渦激振動結果相比，+5°風攻角下，最大豎彎渦振振幅由40 mm降低至21 mm，風速區間由10.0～15.0 m/s前移并縮小至9.0～11.0 m/s。同時，在1∶50節段模型試驗中+3°風攻角下觀測到的豎彎渦激振動現象消失。

圖10(b)可知，加裝風嘴Ⅳ后，通過1∶25節段模型風洞試驗得到的主梁扭轉渦激振動結果與通過1∶50節段模型風洞試驗得到的主梁扭轉渦激振動結果相比，+5°風攻角下，最大扭轉渦振振幅由0.046°降低至0.028°，但風速區間沒有發生變化。同時，主梁在+3°風攻角下的扭轉渦激振動現象消失。綜上所述，1∶25大比例尺節段模型風洞試驗結果驗證了風嘴Ⅳ對主梁渦振的抑制效果。

圖10 工況風嘴Ⅳ斷面主梁渦振振幅(縮尺比1∶25)Fig.10 VIV displacement of the main girder with case wind fairing Ⅳ (scale ratio:1∶25)

4 矩形箱梁渦振誘因及風嘴制振機理

4.1 數值模擬計算工況及參數

為了對鐵路斜拉橋矩形鋼箱梁的渦激振動有更直觀的認識，本文借助計算流體動力學數值模擬軟件，分別對原設計矩形斷面、加裝三角形對稱風嘴斷面與加裝風嘴Ⅳ斷面(見圖11)的非定常繞流進行仿真模擬，再現氣體在橋梁斷面的繞流情況。通過對氣流分離、旋渦的脫落及再附現象的可視化，展現周期漩渦脫落對梁體的作用，并為下行風嘴氣動措施的制振作用作出解釋。

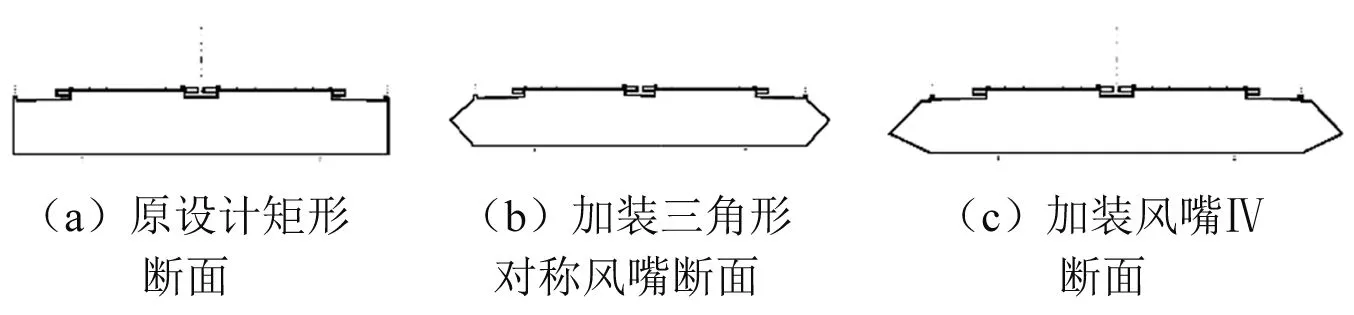
圖11 計算斷面簡圖Fig.11 Calculated cross-section diagram

本文借助Fluent計算流體動力學仿真軟件進行非定常繞流計算，采用了Menter[31]提出的SSTk-ω湍流模型，設置湍流長度尺度為0.05 m，湍流強度為0.5%，計算時間步長為0.000 1 s，選擇 SIMPLE算法，收斂項殘差控制在10×10-5。數值模擬研究僅在0°風攻角下進行，計算模型縮尺比為1∶50，并考慮橋面上的軌道板、中央防拋網、檢修道欄桿和線槽等附屬設置，計算風速按照風洞試驗結果，取發生渦振時的風速3 m/s。由于篇幅限制，本文的研究僅限于對渦振起振時(梁體未振動)的繞流特性以及非定常氣動力，不涉及梁體振動后產生的自激氣動力。

計算區域設置如圖12所示。由外至內分別采用結構化四邊形網格和非結構化四邊形網格，計算域總尺寸為12B×20B(B為原設計矩形斷面模型寬度)，內層網格采用非結構化四邊形網格，為了能夠準確獲得模型表面旋渦的生成、演化和再附現象，第一層網格厚度設置為7.6×10-5m，網格總數在40萬～50萬。計算得到各斷面的y+值均在7以下，此時劃分好的網格可以成功捕獲旋渦的生成、演化發展和再附現象。

圖12 CFD計算域與網格劃分Fig.12 CFD computing domain and mesh generation

4.2 原設計矩形箱梁繞流形態與渦振誘因

通過CFD數值模擬得到的計算風速下原設計矩形斷面的瞬時渦量演化圖，如圖13所示。由于斷面各個位置處的旋渦脫落情況不一致，為了能觀察到所有位置處完整的旋渦脫落情況，選擇旋渦脫落周期最長處的旋渦脫落周期作為觀察周期，即把該斷面下表面迎風側的旋渦脫落周期作為一個觀察分析的周期，某個完整周期內原設計矩形斷面的氣體繞流及旋渦演化過程，如圖13所示。

由圖13可知，來流受到上游矩形截面的阻礙分別向上、下側分流。下側氣流在矩形截面下側轉角附近發生分離，形成一個大型旋渦B1，旋渦B1的寬度為0.7倍主梁寬度，高度與主梁高度幾乎相同，隨著旋渦的發展，旋渦B1逐漸擴大并向下游移動，與斷面下表面板后緣處旋渦B2一起形成了一個大型的旋渦并發生旋渦脫落。上側氣流由于人行道欄桿與中央防拋網的存在，并沒有形成尺寸較大的大型旋渦，而是形成了一系列密集的小旋渦，但也在上表面板后緣處發生了明顯的旋渦脫落現象，與下表面板后緣處脫落的旋渦一起在尾流區形成典型的卡門渦街。其中，梁體下表面發生的較大尺度旋渦脫落再附現象將產生周期性的壓力差，是激勵矩形斷面發生渦激振動的原因。

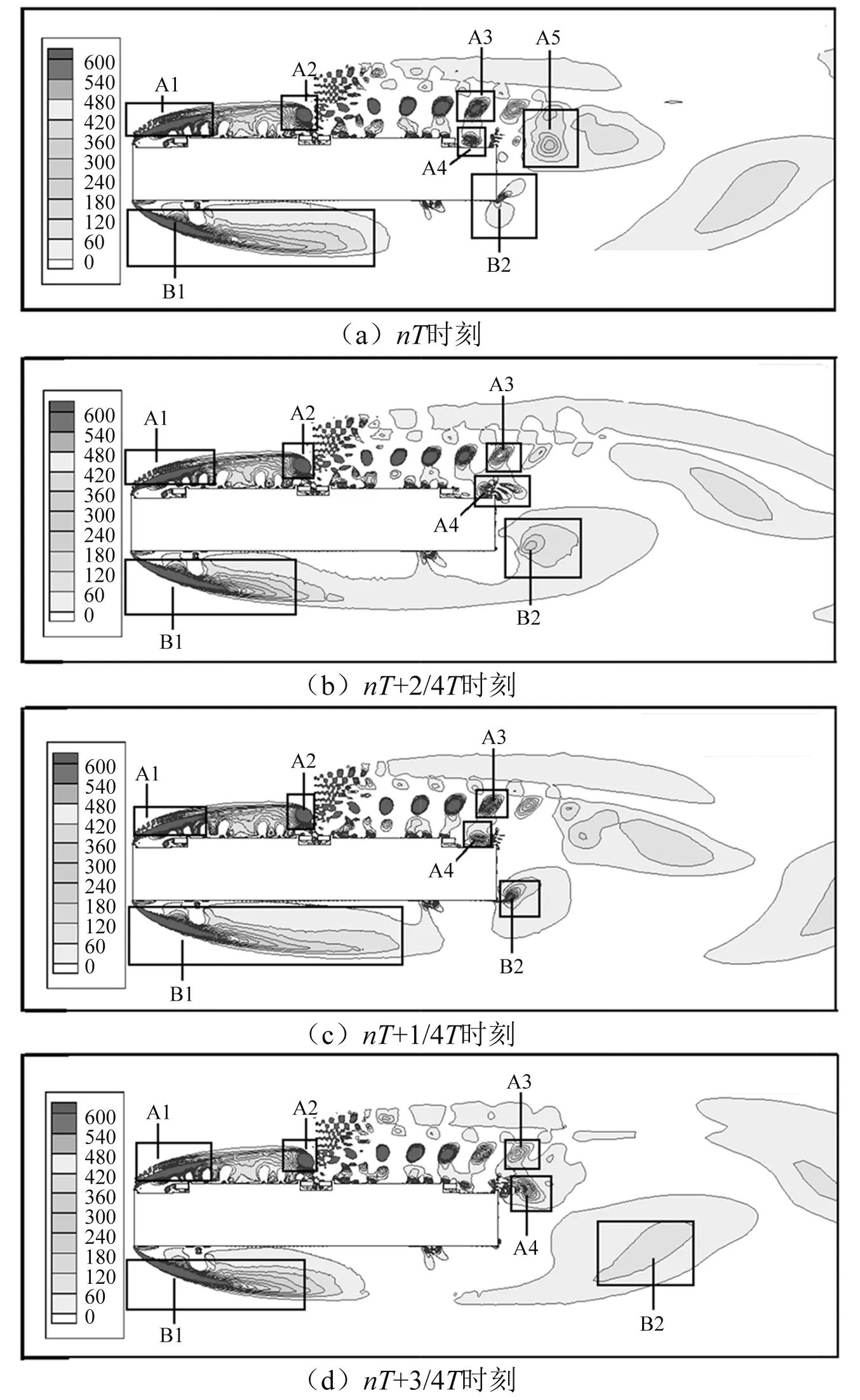
圖13 原設計矩形斷面非定常繞流瞬時渦量演化圖Fig.13 Transient vorticity evolution diagram of unsteady flow around the original rectangular section

橋梁主梁斷面的三分力系數是表示主梁斷面在受到平均風的作用下受力大小的無量綱系數。作用于主梁斷面上的三分力可按選取坐標系不同分為體軸坐標系下三分力和風軸坐標系下三分力。本文中采用體軸坐標系，三分力系數定義表達式為

阻力系數

(1a)

升力系數

(1b)

力矩系數

(1c)

通過三分力試驗和數值模擬分別得到了主梁斷面的靜力三分力系數(對獲得的非定常氣動力取平均值)，如表7所示，并與風洞試驗得到的結果相對比，誤差均在10%以內，因此可以認為數值模擬可以較好地重現主梁段面的非定常繞流狀態和非定常氣動力。

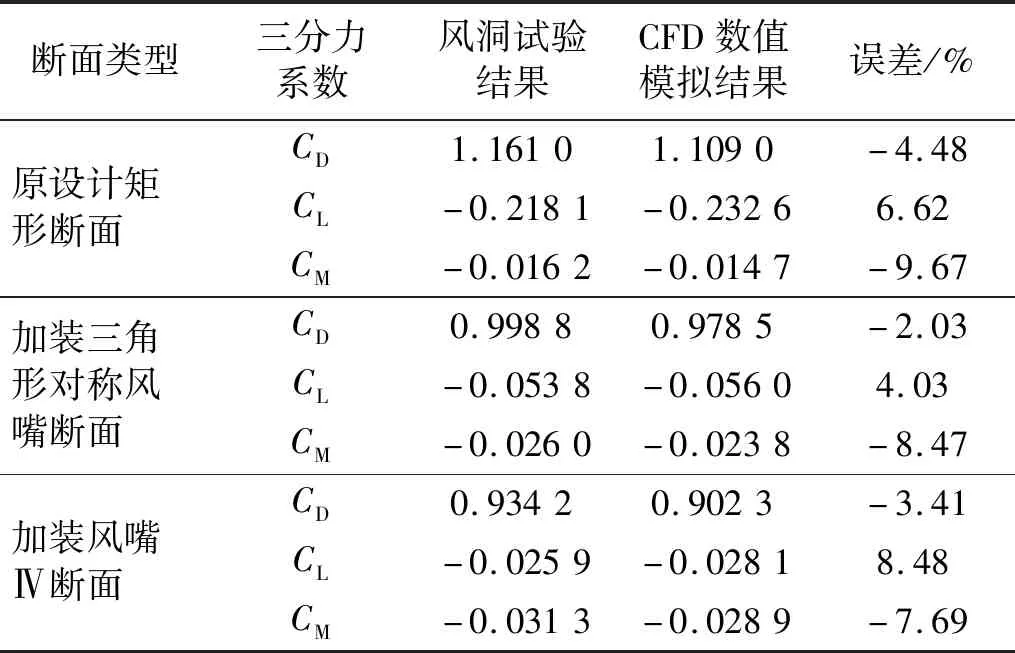
表7 三分力系數表Tab.7 Three-component force coefficient table

通過數值模擬得到原設計矩形斷面的三分力系數時程，如圖14所示。對渦振有較大影響的升力系數變化范圍在-0.170 9～-0.294 1，幅值為0.061 6，力矩系數變化范圍在-0.005 1～-0.024 0，幅值達到0.009 45。

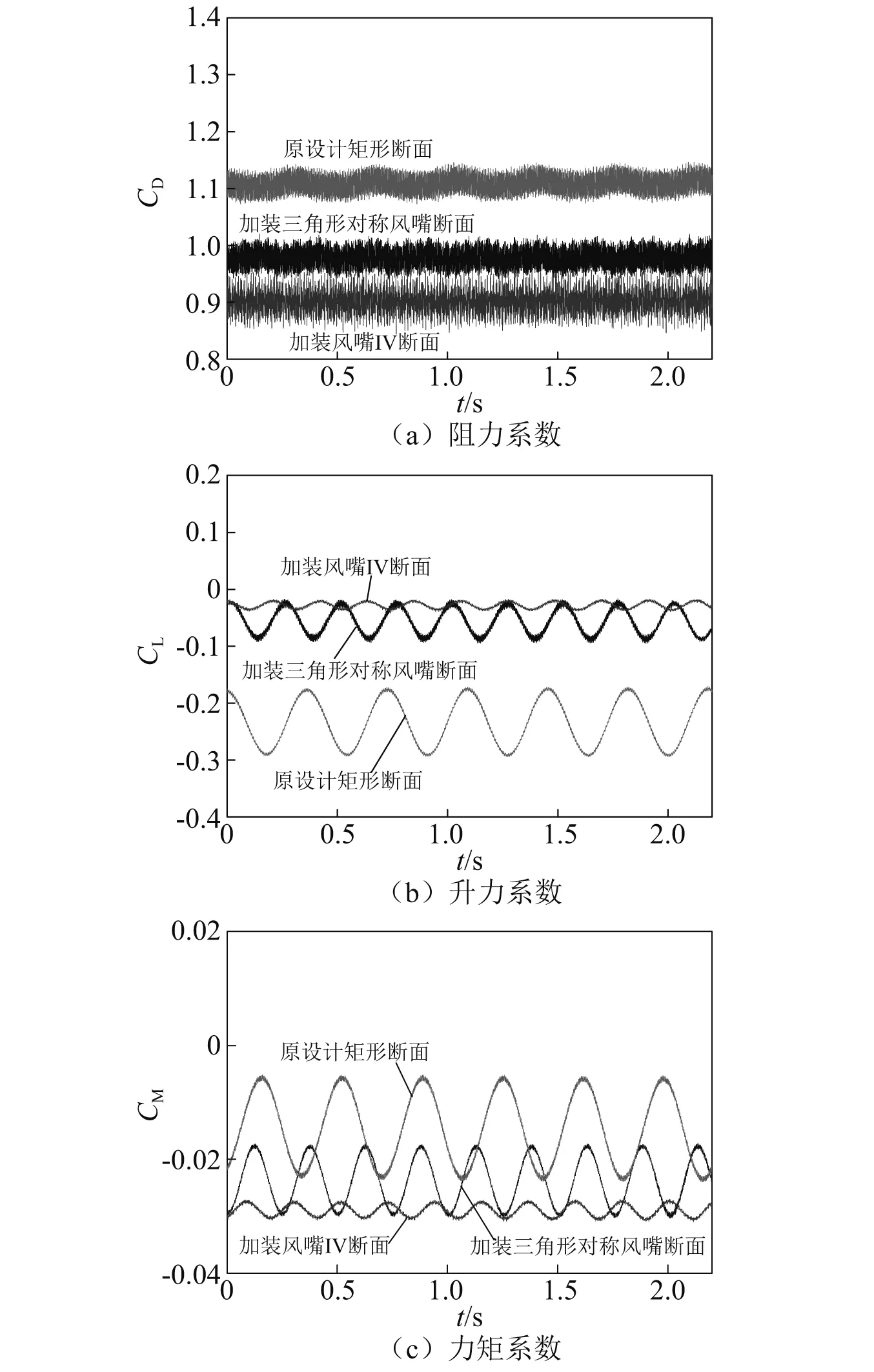
圖14 CFD數值模擬三分力時程圖Fig.14 CFD numerical simulation three-component force time history diagram

4.3 設置風嘴后的繞流特性以及制振機理探討

采用與4.2節同樣的數值分析方法，對三角形對稱風嘴與風嘴Ⅳ這兩種氣動控制措施進行繞流模擬和制振機理分析。

如圖15(a)所示，設置三角形對稱風嘴后，較原設計矩形斷面，氣體繞流特性和旋渦演化路徑已明顯改變。可以發現在斷面上游下表面處生成的旋渦B1尺寸明顯減小，旋渦寬度減小為0.4倍主梁寬度，旋渦高度減小為0.5倍主梁高度，旋渦B1并沒有擴大并向下游移動，而是出現了再附現象，從而導致下表面后緣處脫落的旋渦尺寸減小。但是，相比較于原設計斷面，上表面處的旋渦大小與運動規律沒有發生明顯變化。

通過數值模擬得到三角形對稱風嘴斷面的三分力時程，如圖14所示，與原設計矩形斷面的三分力系數相比較，斷面升力系數變化幅值降低至0.039 3，降幅36.2%，力矩系數幅值降低至0.006 6，降幅30.2%。

三角形對稱風嘴對于表面流場的影響在于，顯著減小了上游側斷面下表面處的旋渦尺寸，減小了上、下表面的壓力差和升力幅值。但沒有減小上、下游壓力合力即扭矩幅值。因此三角形對稱風嘴對于主梁豎彎渦振的抑制能力較好，但對于扭轉渦振的抑制能力有限。

加裝風嘴Ⅳ后斷面非定常繞流瞬時渦量演化圖，如圖15(b)所示，可以發現該斷面氣體繞流特性和旋渦演化規律與原設計矩形斷面及加裝三角形對稱風嘴斷面的區別在于，上游上表面處的旋渦A1明顯減小。同時，消除了下表面迎風側轉角處形成的大尺寸旋渦，顯著減小了下表面后緣處脫落的旋渦尺寸，因此顯著減弱了尾流區卡門渦脫的能量，起到了抑制渦振的作用。

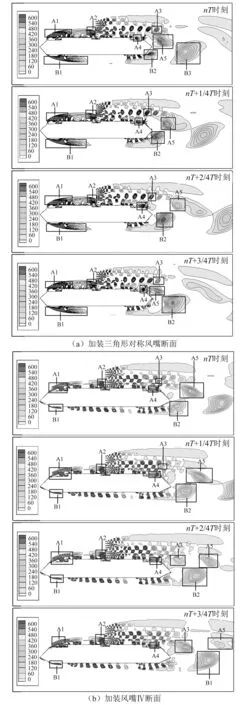
圖15 加裝風嘴斷面非定常繞流瞬時渦量演化圖Fig.15 Transient vorticity evolution diagram of unsteady flow around the section with wind fairings

通過數值模擬得到風嘴Ⅳ斷面的三分力時程，如圖14所示，與原設計矩形斷面的三分力系數相比較，斷面升力系數變化幅值降低至0.028 2，降幅54.2%，力矩系數變化幅值降低至0.001 6，降幅83.1%。

再對比圖14(b)與圖14(c)可以發現相比于力矩系數之間較大的差異，三角形對稱風嘴對梁體升力系數的改變(包括mean值與RMS值)和加裝風嘴Ⅳ后引起的改變更加接近，這也印證了風洞試驗結果，三角形風嘴與風嘴Ⅳ均能降低原設計矩形斷面的豎彎渦激振動，兩種風嘴的渦振制振性能差距主要體現在對主梁扭轉渦激振動的抑制效果。

綜上所述，風嘴Ⅳ與三角形對稱風嘴對原設計矩形斷面的流場影響區別在于，三角形對稱風嘴僅能降低下表面處的旋渦尺寸，而風嘴Ⅳ能同時降低上、下表面處的旋渦尺寸，從而顯著降低斷面上、下表面的壓力差，同時也降低了升力和扭矩幅值，從而抑振了渦振的發生。

5 結 論

對某大跨鐵路斜拉橋矩形鋼箱梁斷面進行節段模型風洞試驗，并借助計算流體動力學數值方法，系統研究了該斷面的渦振性能。對比分析了人行道欄桿、裙板、導流板以及風嘴形式等多種氣動控制措施的影響，主要得出以下結論：

(1) 原設計矩形鋼箱梁斷面在阻尼比0.5%條件下存在較明顯的豎彎及扭轉渦振，且振幅較大。

(2) 三角形風嘴可降低矩形主梁斷面的豎彎渦振振幅，但對降低主梁的扭轉渦振振幅作用有限。

(3) 帶平臺的三角形下行風嘴(風嘴Ⅳ)可顯著降低、甚至消除矩形鋼箱梁的渦激振動。

(4) 計算流體動力學的模擬結果表明，矩形鋼箱梁斷面發生的大尺度漩渦及由此產生的周期性氣動力是導致其發生渦振的主要原因；帶平臺的三角形下行風嘴能顯著減小主梁斷面的旋渦尺寸，減小周期性的升力和力矩，從而起到了抑振主梁渦振的作用。