基于自適應引力算法的橋梁監測傳感器優化布置

高 博，柏智會，宋宇博

(蘭州交通大學 機電工程學院，蘭州 730070)

橋梁的健康監測是測量橋梁在損傷條件下的動力特性和結構參數改變量，對比其在無損狀態下的信息，并制定出最佳的維護方案[1]。傳感器優化布置方案對橋梁健康監測的測試精度和參數分析有著直接影響。考慮到經濟性和結構特征，要求橋梁上安裝的傳感器數量有限，因此，如何利用有限的傳感器測點代表整體結構的運行狀況和完整信息顯得十分重要。傳感器優化布置原理是從N個待測點中挑選出M個布設點，使目標函數達到最優的過程。其實質是組合優化問題，由于最終布置結果的復雜性和多樣性，成為當今學者的熱門研究課題。

目前已有許多成熟的傳感器布置方法，其中傳感器優化布置方案主要分為兩類，一類是傳統優化方法：Kammer等[2]提出的有效獨立法是以模態矩陣為理論基礎，將測點獨立性的貢獻值作為判定準則，依次刪除貢獻最小的測點，最終留下線性無關性最大的點作為傳感器布置方案；Carne等[3]提出的模態置信準則(modal assurance criterion ，MAC)，將MAC矩陣的非對角元素最小化作為目標函數，發現MAC可以較好的反映梁模態向量的識別性；Guyuan縮減法[4]是利用剛度質量比小的位置更能反映結構的模態特性，將傳感器布置在縮減后的位置。上述方法得到的結果往往是局部次優點，存在優化效率較低，尋優性能差的缺點，并不能達到理論與實際值誤差最小的要求。第二類群智能優化算法，憑借其優秀的搜索和開發能力，在傳感器布置中取得了快速發展：Dinh-Cong等[5]將Jaya算法應用到傳感器優化布置和復合結構的損傷識別，發現可以成功找到損傷部位；Bruggi等[6]在傳感器布置時采用拓撲方法進行優化，并在板結構的損失識別驗證了算法的可行性；Wang等[7]提出了基于頻率和空間域分解的方法，對四跨橋結構進行模態分析和損傷識別；Jin[8]提出了使用模態置信準則結合改進的和聲搜索算法，應用在起重機傳感器布置并驗證了其優越性；Yi等[9]將自適應猴群算法采用雙重編碼的方式應用在高層建筑，發現更穩定的最優解；楊振偉等[10]引入等級劃分和免疫機制，將改進的螢火蟲算法應用在橋梁傳感器布置，尋優效率取得顯著提高。黃民水等[11]提出了基于二重編碼的遺傳算法應用于橋梁結構的健康監測；趙建華等[12]把慣性權重遞減的粒子群算法結合模態置信準則，發現在二維桁架結構中能找出傳感器的優化位置。以上基于群智能算法的傳感器布置方法依然存在一定的局限性，如對于同一研究對象，不同的研究方法得到的傳感器布置方案往往不同，因此算法的可靠性驗證仍需進一步改善。

引力搜索算法(gravity search algorithm,GSA)[13]憑借其容易實現，可操作性好，優化效果明顯的優點，在生產實踐中得到廣泛應用[14-17]。GSA算法也存在搜索能力較弱的缺點，本文對GSA算法進行改進，通過對引力常量G中衰減因子α的自適應調整，以改變粒子不同時期的步長，來改善算法性能，提高算法搜索能力。將改進后的自適應引力算法(adaptive gravity search algorithm,AGSA)通過雙重編碼的方式，結合MAC準則，提出了基于AGSA算法的傳感器優化布置方案。以馬水河大橋為實例，驗證AGSA算法的有效性，發現改進后的AGSA算法在傳感器優化布置優于遺傳算法(genetic algorithm,GA)得到的結果。

1 傳感器優化準則

現有的傳感器優化準則如模態動能法由于高度依賴有限元網格的劃分精度，會影響數據的可靠性；模態縮減準則存在容易丟失待測模態的缺點，增加識別難度。在實際生產中，由于受到外在因素：測量儀器的精度誤差、測試場所的噪聲干擾等，會導致得到的模態向量夾角過小，甚至為0的情況，而導致模態信息丟失的情況。故傳感器優化布置的測點應選取空間中模態夾角較大，易識別的點。MAC可以選擇較大的空間交角,盡可能保留原模型的特性。保證了模態的正交性和模態信息的完整性。故可以將MAC作為傳感器優化布置的適應度函數，用來評價各階測試振型的獨立性。MAC的表達式為

(1)

式中，φi和φj分別為第i階和第j階模態向量。

研究表明，MACij(i≠j)的值介于0～1，反映對應模態向量的空間夾角。其中MACij(i≠j)的值越接近于0，說明對應的空間夾角越大，i階和j階模態向量越接近正交；MACij(i≠j)的值越接近于1，說明對應的空間夾角越小，i階和j階模態向量越接近平行。一般地，當MACij(i≠j)值小于0.25，即可認為兩模態向量容易識別。MAC矩陣的非對角元素值越小，表明計算的模態向量獨立性越好，其模態振型越容易識別。因此可以將MAC矩陣的最大非對角元素最小化作為橋梁傳感器布置的適應度函數，表達式為

fitness=minf(x)

(2)

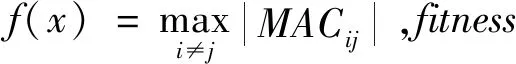
2 基于自適應的引力搜索算法

引力搜索算法是利用粒子之間受到萬有引力的吸引作用，種群中質量最大的粒子占據最優位置，其他粒子在萬有引力的作用下向質量最大的粒子移動，得到所求問題全局最優解的過程[19]。假設算法中有M個粒子，以其中某一粒子i為例，粒子i受到其他粒子的萬有引力，在合力作用下產生加速度a和速度v，使粒子i下一時刻向全局最優解靠近的過程。引力常量G自始至終貫穿于算法的整個搜索過程，其取值的變化過程會直接影響算法的搜索效率和尋優精度，GSA算法中的衰減因子α的取值時一個常數，這會導致粒子在搜索過程以固定的步長移動。為了增強算法的優化能力，本文提出的AGSA算法對α進行自適應調整，搜索初期粒子距離最優解較遠，粒子以較大步長進行全局搜索；搜索后期粒子靠近最優解的鄰域，粒子采取小步長搜索，有利于算法局部搜索，有效找到全局最優解。

2.1 引力搜索算法

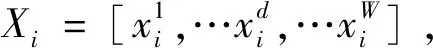
(3)

式中：Mi(t)和Mj(t)分別為粒子i，j的慣性質量；G(t)為t時刻的萬有引力系數；R為粒子i與粒子j之間的距離；ε是為了保證分母不為0的非常小的數。

G(t)的計算公式為

(4)

式中，α為常數;Imax為最大迭代次數。

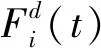
(5)

式中，best為對粒子i有引力作用的粒子的集合。

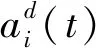
(6)

式中，Mass(i)為粒子i的慣性質量，其計算公式為

(7)

(8)

式中，fitnessb(t)和fitnessw(t)分別為最好的適應度值和最差的適應度值。

下一時刻粒子i的速度和位置公式為

(9)

式中，rand1，rand2為[0，1]的隨機數。

2.2 改進的自適應引力搜索算法

引力常量G(t)對算法的收斂速度和尋優精度具有重要影響。式(4)中的α具有調節算法收斂速度的作用[20]。針對GSA算法的尋優效率和搜索精度問題，本文對GSA算法進行了改進，提出了AGSA算法。考慮到GSA算法中α的取值是一個常數，這就會導致粒子距離最優解較遠時，步長太小，移動過慢，花費時間太長；粒子距離最優解較近時，步長太大，可能出現偏離最優解，陷入局部最優解的情況。因此，改進后的AGSA算法在搜索前期選取較小的衰減因子α，粒子以較大的步長進行全局搜索，有利于減少算法的搜索時間，提高整體尋優效率；算法的后期選取較大的衰減因子α，粒子對應較小的步長完成局部搜索，避免算法落入局部極值點。自衰減因子α的自適應原理是迭代初期對應的衰減因子α取較小值，對應的G取值較大，有利于粒子進行全局搜索；迭代后期衰減因子α不斷增加接近β，對應的G取值較小，有利于粒子進行局部搜索。自適應衰減因子α表達式為

(10)

式中：t為當前迭代次數；β為初始參數，根據經驗，當β=40時，算法的尋優效果最佳，β的取值具有通用性，不受橋梁規模和所選橋型的影響。

AGSA算法的原理圖如圖1所示

圖1 AGSA算法原理圖Fig.1 Schematic diagram of AGSA

圖1中，粒子M1在M2，M3，M4的萬有引力作用下產生了合力F1和加速度a1，通過衰減因子α的自適應機制，粒子M1以不同的步長向全局最優解靠近。

3 基于自適應引力的傳感器優化布置

3.1 種群初始化及編碼

GSA算法當前主要應用在連續優化問題的求解，傳感器優化布置是類似于0-1規劃的離散型問題，因此需要將引力搜索算法改進為適合整數規劃的優化算法。本文采用一種雙重編碼的方式,雙重編碼的方法如表1所示。

表1 雙重編碼方式Tab.1 Dual-structure coding method

利用附加碼xi和變量碼si組成的有序對(xi,si)表示種群中個體i對應的傳感器布置結果[21],(xi為i的位置向量;si為二進制向量0或1，其中，0為不布置傳感器，1為布置傳感器)，這種雙重編碼的方式使得AGSA算法可以解決傳感器優化布置問題。例如，已知有8個待選點，它們的附加碼為x=(5,3,6,1,4,7,2,8),其雙重結構編碼結果如表2所示，由表2可以知道變量碼對應的布置方案為s=(3,4,5,8)。

表2 雙重編碼結果Tab.2 The result of dual-structure coding method

3.2 基于AGSA算法的傳感器優化布置過程

步驟1選擇和導入模態矩陣。模態矩陣階數的選擇對傳感器布置結果有重要影響，一方面，適合的模態矩陣可以代表結構的整體性能，保證布置方案的準確性；另一方面，不同的模態階數，得到的布置方案有差異性。首先，建立馬水河特大橋的有限元模型，利用模態分析的方法得到模型所有節點的模態振型矩陣，將得到的模態振型矩陣作為輸入值，所有節點對應的自由度作為傳感器布置的待選點，其次，假設待選點的數量為n，傳感器布設點數量設置為m，對這n個候選位置依次從1-n進行整數編號。

步驟2設種群數量為N，粒子i對應的解可以表示為xs(i)=(xi,si)={(xi1,si1),(xi2,si2),…,(xin,sin)},xi的各個分量是區間[down,up]產生的隨機整數，si的分量是由轉換函數得到的二進制向量。

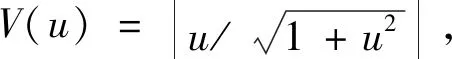
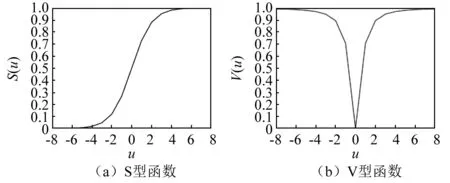
圖2 轉換函數Fig.2 Conversion function

劉勇等[22]發現并驗證了V型轉換函數的優化效果更好，故本文選取V型函數作為轉換函數。si的分量按照下式轉化為二進制向量

(11)

式(11)中，不同的位置分量xij計算得到的二進制值不同，因此需要設置一個閥值δ來滿足

(12)

式中，j∈{1,2,…,f}，本文中δ=0.5，將xi的各位置分量代入式(11)中，若函數值大于0.5，附加碼值為1，表示在該候選點布置傳感器；若函數值小于0.5，附加碼值為0，表示在該候選點不布置傳感器。通過計算可以得到xij的取值在[-8,8]時取值時，si的分量取值0≤V(xij)≤0.992 3，可以近似代替[0,1]。故down=-8，up=8。

步驟3按照步驟1和步驟2，隨機產生種群數量為N的粒子位置，其中，每個粒子的位置都表示一種傳感器布置方案。

步驟4把種群中的N個粒子依次代入適應度函數fitness(xsi)。在計算過程中，位置向量通過轉化函數V(xij)轉化為二進制向量sij，將sij代表的傳感器位置對應的模態矩陣計算適應度函數，最好的適應度值標記為fitnessb(xsi)，最差的適應度值標記為fitnessw(xsi)。最好適應度值對應的布置方案記為pi(xsi)，pi(xsi)代表種群中粒子的個體最優解，是每個粒子迭代中的最優解。pg(xsi)表示全局最優解，是種群中所有粒子中的最優解。

步驟5利用式(7)和式(8)，計算每個粒子的慣性質量；按照式(9)對衰減因子α進行自適應改變，更新引力常量G(t)。

步驟6以粒子i為例，其對應的位置分量xi={xi1,xi2,…,xim}，其中m為需要布設的傳感器數目，計算粒子i與其他粒子的歐式距離，利用式(3)和式(5)，得到粒子i在其他粒子作用下的合力，利用式(6)計算粒子i受到的加速度。同理計算出種群中其他粒子受到的萬有引力和加速度。

步驟7為加快粒子收斂速度，在粒子速度公式中引入變異算子η，增加全局最優解對粒子的引導作用，變異算子的表達式如式(13)所示，在更新位置的過程中，計算得到的加速度和速度分量會出現非整數的情況。因此，本文中位置更新如式(14)所示。

(13)

(14)

式中，round為取整函數，保證更新后的粒子位置分量是整數形式。

步驟8將更新后的粒子對應的模態位移代入式(2)，若更新后的fitness(xsi)值小于更新前的，則粒子位置發生改變，否則，粒子位置保持不變。更新后的最優適應度值對應的布置方案記為pb(xsi)，若更新后的最優適應度值fitness(pb)小于更新前的全局最優值pg(xsi)對應的適應度值fitness(pg(xsi)),則用當前粒子代替全局最優解，反之，全局最優解保持不變。

步驟9判斷算法是否達到預設的精度要求或最大迭代次數，若滿足，停止迭代，輸出全局最優解，即為需要的傳感器布置方案；若不滿足，返回到步驟5。

注1粒子的位置分量是從[-8,8]中隨機產生的整數，在步驟7中，粒子在位置更新中，可能會出現超出取值范圍的情況。因此，本文規定，當位置分量大于8時，取8；當位置分量小于-8時，取-8。

基于AGSA的流程圖如圖3所示。

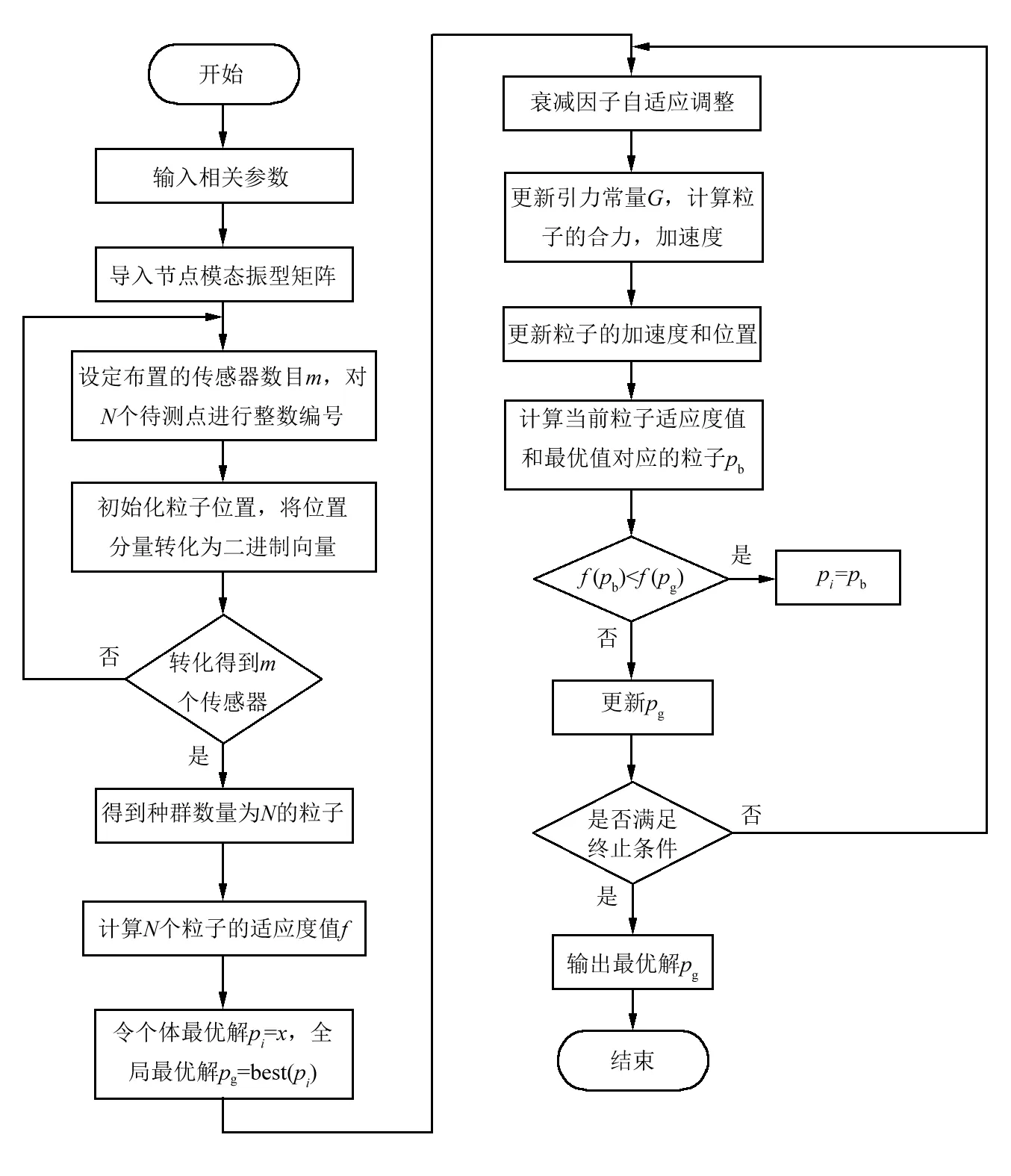
圖3 基于AGSA的流程圖Fig.3 Flow chart based on AGSA

4 模型驗證

4.1 計算模型

為了驗證本文提出的算法在傳感器優化布置的有效性，本文以馬水河大橋為例，如圖4所示，橋梁全長955.80 m，橋面中心設計標高654.355 m，主橋上部采用110 m+3 m×200 m+110 m，全橋為單箱單室，橋面寬12.5 m，梁底寬6.5 m，梁高3.50～12.00 m；主橋下部共有4座橋墩，承臺厚度為4.0 m。考慮到馬水河特大橋在施工時會受到溫度，預應力拉伸等因素的影響，將橋梁模型簡化為平面剛架，各施工段按照梁單元計算，導入到ANSYS進行模態分析。模型共有442個節點，436個單元，每個節點包含3個自由度，分別對應x，y，z方向的模態信息。并導出結構的前10階模態振型。由于x和z方向模態位移均接近于0，因此本文只考慮y方向的模態位移。橋梁結構的前10階固有頻率及振型描述如表3所示。

圖4 橋梁計算模型Fig.4 Bridge calculation model

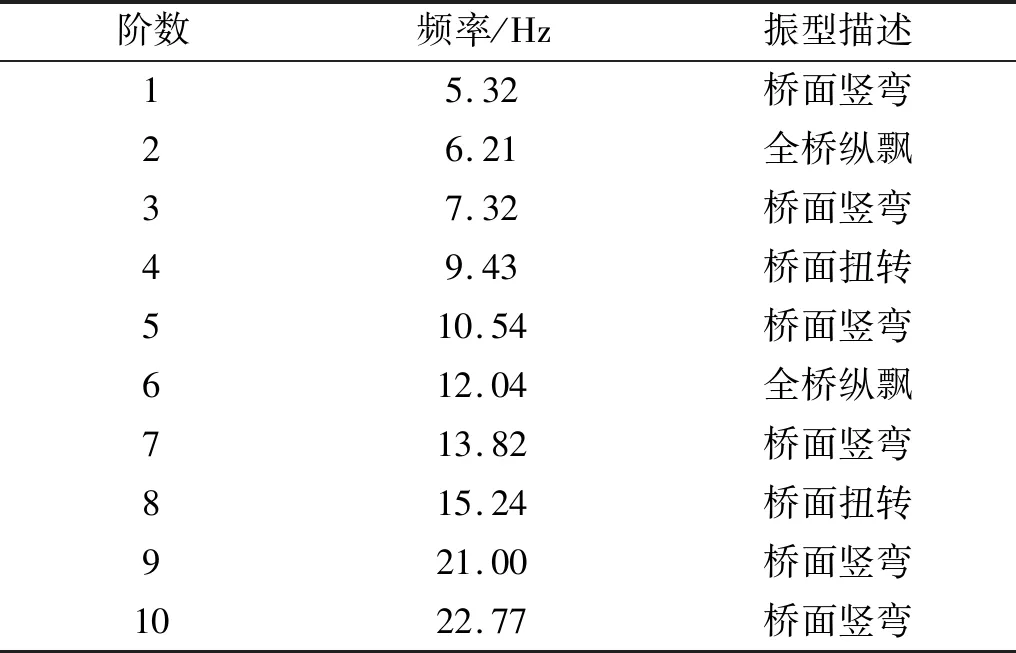
表3 橋梁固有頻率及振型描述Tab.3 Description of natural frequency and vibration mode of bridge

4.2 自適應引力算法布置方案

根據本文提出的自適應引力搜索算法進行傳感器布置。設定種群數量為N=100，迭代次數為Imax=20，β=40,G0=100,算法重復運行10次，分別計算布設點m為8,12,16時，目標函數的最優值，最差值，以及平均值。其最優布置方案和迭代曲線分別如表4和圖5所示。

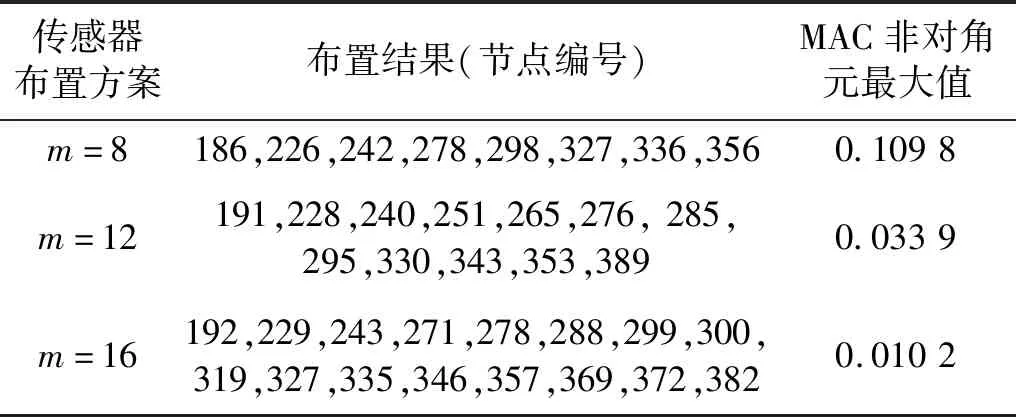
表4 傳感器布置方案Tab.4 Sensor placement

由圖5可知，不同的傳感器數量對應的適應度函數值不同，當布置的傳感器數量m分別為8，12，16時，目標函數的平均值分別為0.132 4，0.046 6，0.018 8。結果表明隨著m的增加，目標函數的平均值越小，搜索得到的模態向量更容易識別；目標函數的最優值依次可以達到0.109 8，0.033 9，0.010 2。說明在一定的取值范圍內，隨著傳感器數量的增加可以得到的布置方案更優。

圖5 自適應引力算法迭代曲線Fig.5 Iterative curves of adaptive gravitation algorithms

一般來說，傳感器布置的數量越多，可以得到結構的布置信息越多，越能反映結構的健康狀況。但在實際應用中，由于傳感器成本較高，不可能布置太多的傳感器，傳感器數量的選擇顯得至關重要。故本文以傳感器數量為自變量，以式(2)為目標函數，每組變量計算10次，10次運行結果的平均值為應變量，變化曲線如圖6所示。可以看出傳感器數量在0～8時，目標函數的下降曲線較快，當傳感器數量在15～20時，目標函數值趨于穩定。因此，本文選取m=16作為最終布置的傳感器數量。

圖6 傳感器數量與目標函數曲線Fig.6 The curve of sensors number and objective function curve

同時，為了驗證所選模態階數對傳感器優化結果的影響，本文探討了傳感器數量設定m=16，模態階數分別為6,7,8,9,10時，通過AGSA算法最終得到的傳感器優化布置結果和對應精度如表5所示。

由表5可以看出，隨著模態階數的增加，MAC矩陣非對角最大值出現增大的趨勢。但從表中可以看出不論模態階數選取6階還是10階，最終得到的目標函數值遠小于0.25，也證明了AGSA算法的有效性。

表5 模態階數對優化結果的影響Tab.5 Effect of modal order on optimization results

4.3 優化布置結果分析

為了進一步突出AGSA算法的優越性，比較AGSA算法和GA算法在布置16個傳感器時的結果。圖7給出了兩種算法的MAC矩陣柱形圖。一種是GA算法[23]得到的傳感器布置方案;另一種是AGSA算法得到的傳感器布置方案。GA算法得到的MAC矩陣非對角元最大值為0.169 0，雖然小于0.25，但是個別位置還存在不宜分辨的情況；相比GA算法，AGSA算法的非對角元最大值為0.010 2，效率提升93.96%，也說明本文提出的基于AGSA算法是有效性和可行性。考慮到圖7中MAC矩陣的非對角元素值太小，圖8給出了兩種算法布置方案對應的MAC矩陣每個模態列向量非對角元最大值。由圖8可以清楚的看出AGSA算法的MAC矩陣的最大非對角元明顯小于GA算法得到的結果。這也驗證了AGSA算法對應的模態向量區分度更高，布置方案更優。表6給出了兩種算法的傳感器布置方案。

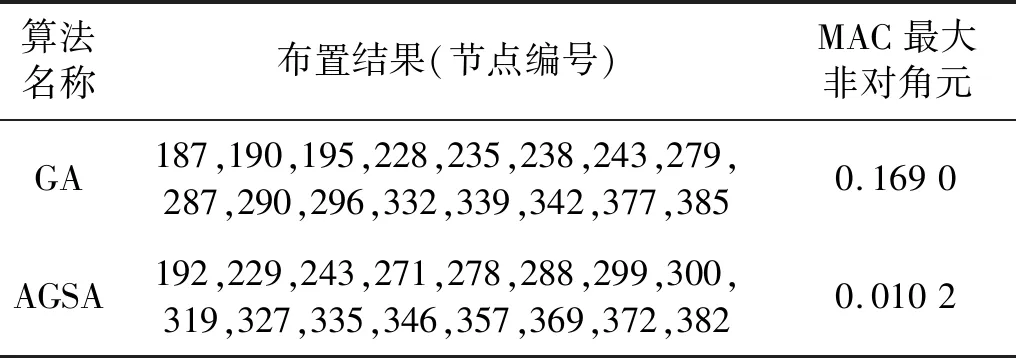
表6 兩種算法的布置方案Tab.6 Sensor placement of two algorithms

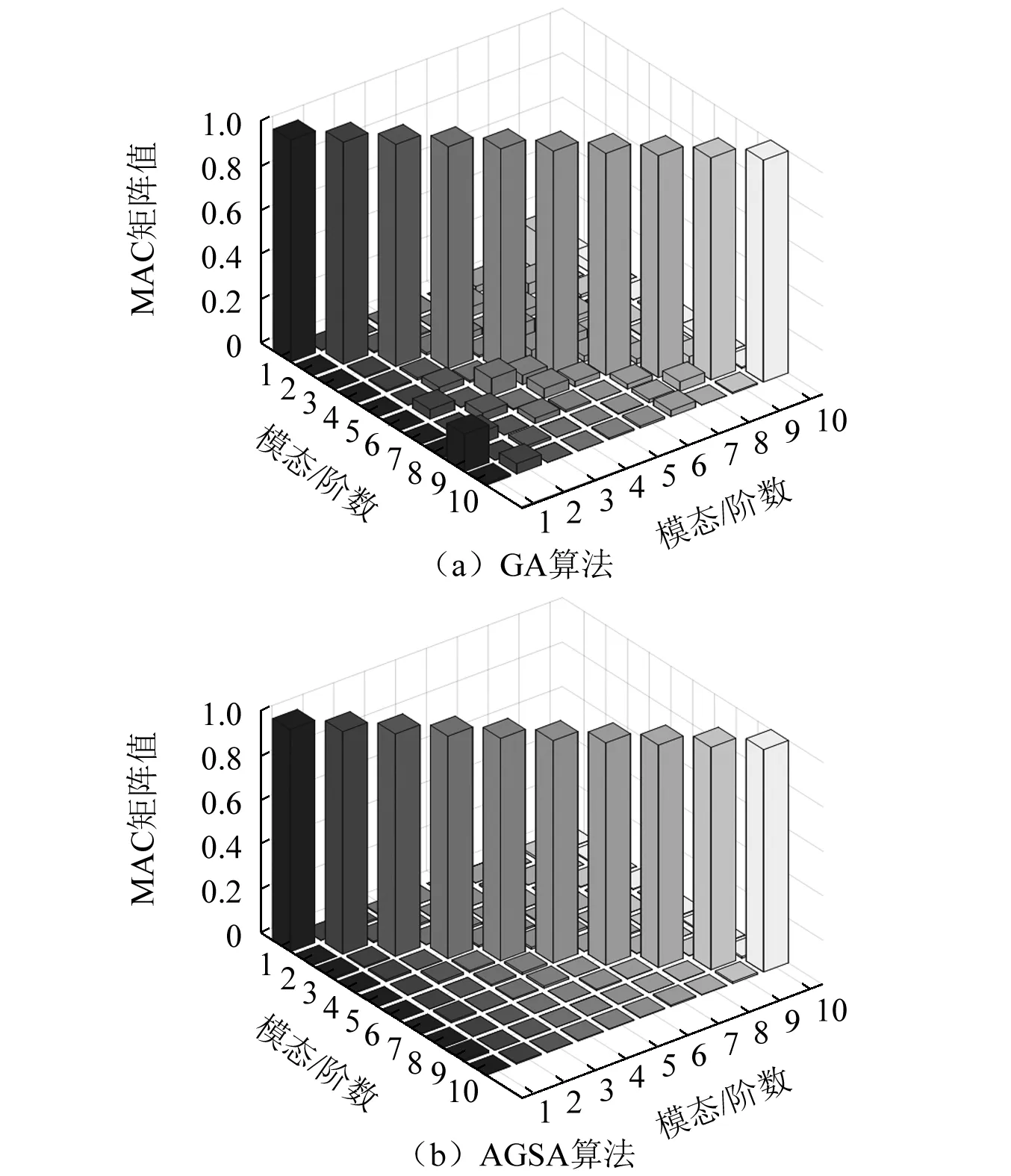
圖7 兩種算法的MAC矩陣Fig.7 MAC matrix under two algorithms

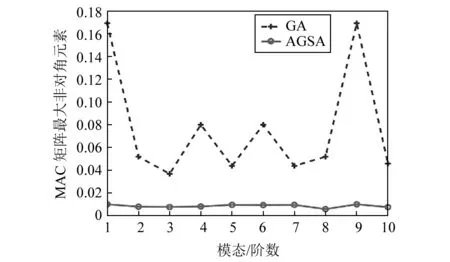
圖8 MAC矩陣每個列向量最大非對角元Fig.8 Maximum MAC off-diagonal value in each of the modes

5 結 論

本文針對GSA算法只能解決連續性函數的優化問題，提出了可以解決離散型問題的AGSA算法，并將其應用到馬水河大橋的傳感器優化布置中，將其布置結果與遺傳算法得到的結果比較，得到以下結論：

(1)針對GSA算法搜索效率和尋優精度不高，本文提出的AGSA算法對引力常量G中的α進行了改進，確保粒子在不同的搜索時期，進行全局搜索和局部精細搜索，提高了算法的全局搜索能力。

(2)為了AGSA算法可以解決離散型的傳感器優化布置問題，本文采用雙重編碼的方式，將AGSA算法應用到傳感器布置中，克服了二進制編碼導致的迭代過程中，傳感器數量發生改變的缺點。試驗結果表明，該方法可以有效解決傳感器優化布置問題。

(3)AGSA算法通過多次試驗，發現傳感器數量選擇對目標函數的精度影響較大,在初始階段，目標函數值隨傳感器數量的增加而不斷減小；當數量增加到一定范圍，目標函數值趨于穩定。

(4)以馬水河大橋為例，將AGSA算法和遺傳算法得到的布置方案相比較，結果表明，AGSA算法的可靠性，尋優效率都優于遺傳算法，證實了本文提出的AGSA算法適用于傳感器優化布置，也表明該算法可以滿足大型橋梁健康監測的需求。