高光譜圖像分類的Wasserstein配置熵非監督波段選擇方法

張 紅，吳智偉，王繼成，高培超

1. 華東師范大學全球創新與發展研究院，上海 200062； 2. 華東師范大學城市與區域科學學院，上海 200241； 3. 西南交通大學地球科學與環境工程學院，四川 成都 611756； 4. 北京師范大學地表過程與資源生態國家重點實驗室，北京 100875

高光譜圖像已被廣泛用于地質、生態、大氣、醫學、農業等領域[1-2]。其波段數目眾多且相鄰波段相關性較高，需進行降維處理[3]。常見的高光譜數據降維處理方法有考慮所有波段的數學變換方法及波段組合方法[4]。前者過程復雜、計算量大，且改變了高光譜圖像的物理意義。后者更為常用，包括監督和非監督兩類[5]。

非監督波段選擇多基于波段排序和聚類[6]。波段排序方法例如信息離散度法(information divergence，ID)[7]、線性約束最小方差法(linearly constraint minimum variance，LCMV)[8]和最大方差主成分分析法(maximum variance principal component analysis，MVPCA)[7]。這些方法雖然直觀簡便，但忽略了波段間相關性，導致冗余波段。波段聚類先將相關性強的波段聚成一組，再挑選各組的代表性波段。聚類多基于互信息(Ward’s linkage strategy using mutual information，WaLuMI)和KL散度(Ward’s linkage strategy using divergence，WaLuDi)[9]。人工智能也被用于波段聚類與選擇，如文獻[10]基于深度學習對高光譜數據降維處理。文獻[11]結合深度卷積自編碼器和子空間聚類進行波段選擇。文獻[12]采用深度對抗子空間聚類(deep adversarial subspace clustering，DASC)網絡以提升子空間聚類的自表達能力，文獻[13]基于全連接深度網絡和深度神經網絡提取波段間的非線性特征。

最優波段組合為信息豐富且各波段間的相關性最小的波段集合[14]。作為傳統信息測度指標，香農熵僅考慮了空間組分信息(像元的種類和比例)[15-17]，忽略了空間配置信息(像元的空間分布)，無法準確刻畫圖像相似性[18]。如圖1所示，圖1(a)與1(b)的組分不同、但配置相同；圖1(a)與1(c)的組分相同、但配置不同。

圖1 具有相同組分或配置信息的不同圖像Fig.1 Different images with the same composition or configuration information

香農熵因熱力學基礎薄弱、忽略了空間配置信息等受到質疑[16]。玻爾茲曼熵(簡稱玻熵)被引入以克服上述不足，包括基于邊緣總數的玻熵[19]、基于多尺度層次結構的玻熵[20]等。文獻[21]提出了基于Wasserstein指標的配置熵(簡稱W熵)測度指標，本文將其引入高光譜圖像波段選擇，將W熵從四鄰域拓展至八鄰域。基于W熵差異值測度高光譜圖像波段間的相關性，通過非監督次優搜索法確定最優波段組合，使用支持向量機(support vector machine,SVM)分類，評價其分類精度。

1 空間信息與相關性測度

當前測度波段信息和波段相關性主要有兩類方法，即香農熵和玻熵。

1.1 空間組分信息：從香農統計信息熵到香農空間信息熵

信息是“事物運動狀態或存在方式的不確定性”[15]，信息量是對信息統計特征的描述，公式為

(1)

式中，P(x)表示隨機變量X取值為x的概率。

文獻[22]構建了地圖符號多樣性信息熵測度指標。文獻[17]指出地圖信息包括統計、幾何、拓撲和專題信息等，提出基于Voronoi圖的信息熵計算方法，是現有對地圖信息的最佳量測[15]。文獻[23]構建了香農熵變體。

1.2 空間配置信息：玻爾茲曼熵

玻熵源于熱力學[24]，公式為

S=kBlnW

(2)

式中，S為某宏觀狀態的玻熵；kB為玻爾茲曼常數；W為該宏觀狀態中所包含的微觀狀態總數。W熵是玻熵的變體，基于Wasserstein距離構建，即兩個概率分布之間轉換的最小代價[25]，公式為

(3)

式中，(Pr,Pg)是邊緣分布Pr和Pg的聯合分布；∏(Pr,Pg)是聯合分布(Pr,Pg)的集合。W熵指標[21]公式為

Wdist=(1-Wc)(1-Ws)

(4)

式中，Wc和Ws分別為改進版玻熵計算公式中第2項對應的直方圖、第3項對應的直方圖與狄拉克分布變體之間的Wasserstein距離的歸一化結果。

圖2(a)尺寸為512×512像素，分別取其灰度矩陣的前128、256、384及512列像元灰度值進行隨機排列，得到圖2(b)至圖2(e)。圖2(a)至圖2(e)的W熵分別為0.422 0、0.422 4、0.423 0、0.424 5和0.426 6，與目視觀察到的無序性程度一致，表明W熵可刻畫圖像空間配置復雜性。

圖2 某圖像及部分像元隨機排列后的圖像Fig.2 A image and its randomly permuted images

1.3 信息的相關性：互信息、相對熵與玻熵差異值

兩個隨機變量的相關性可由互信息或相對熵測度。

1.3.1 互信息

互信息描述了兩個隨機變量之間的統計相關性，即某隨機變量包含另一隨機變量信息的不確定性程度，公式為

(5)

式中，p(x,y)是兩個隨機變量X、Y的聯合概率分布函數；p(x)和p(y)分別是隨機變量X、Y的邊緣概率分布函數。變量相關性越強，包含的共同信息越多，互信息值越高。互信息具有對稱性。

1.3.2 標準化互信息

因變量類型與取值范圍的差異，對互信息進行標準化處理[26-27]，包括

I1=I(X,Y)/min{H(X),H(Y)}

(6)

I2=2×I(X,Y)/(H(X)+H(Y))

(7)

I3=I(X,Y)/max{H(X),H(Y)}

(8)

(9)

式中，I(X,Y)是兩個隨機變量X和Y的互信息；H(X)和H(Y)為X和Y的香農熵。

1.3.3 相對熵

相對熵(又稱為KL散度)是兩個概率分布差異的非對稱性測度[28]，公式為

(10)

式中，P(X)和Q(X)分別為隨機變量X的兩種概率分布。

1.3.4 相對熵變體

為避免Q(X)=0，文獻[9]提出兩個應用范圍更廣的相對熵變體

(11)

(12)

式中，P(X)和Q(X)分別是隨機變量X的概率分布。

表1列出圖2中影像兩兩間相似性計算結果，證實了互信息和標準化互信息的有效性。

表1 圖2中各影像的互信息、標準化互信息及相對熵變體值

1.3.5 玻熵差異值

絕對或相對玻熵差異值也可刻畫波段相似性[9]，公式如下

DBEA(X,Y)=|SA(X)-SA(Y)|

(13)

DBER(X,Y)=|SR(X)-SR(Y)|

(14)

式中，X和Y代表不同波段；SA和SR代表絕對和相對玻熵。

W熵差異值公式為

DW(X,Y)=|W(X)-W(Y)|

(15)

式中，X和Y代表不同波段；W代表各波段的W熵。

2 Wasserstein配置熵的改進及其用于波段選擇的基本思路

傳統W熵局限于四鄰域，本文將其拓展到八鄰域，并提出基于W熵的高光譜圖像波段選擇方法。

2.1 W熵的改進：從四鄰域到八鄰域

鄰域廣泛見于斑塊鑲嵌體格局、地理相似性或空間自相關分析中[29]。常見的鄰域定義方式有Rook(僅共邊)鄰近、Bishops(僅共頂點)鄰近和Queen’s(或King’s)(共邊或共頂點)鄰近[30]。前二者為四鄰域，后者為八鄰域，對應的W熵分別記為Wdist和W8dist。

圖3中，各影像對應的Wdist值分別為1.000 0、0.955 3、0.977 4和0.977 4，對應的W8dist值分別為1.000 0、0.955 3、0.955 3和0.977 4。表明W8dist可有效識別連續區域引起的信息冗余。

2.2 基于W熵的波段選擇思路

采用文獻[5]提出的非監督次優搜索法來確定信息量較大且相關性較低的波段組合。具體過程如圖4所示，其中α和β分別代表原始波段集合和最優波段集合。

圖3 4幅模擬圖像Fig.3 Four simulated images

圖4 基于Wasserstein配置熵的高光譜圖像非監督波段選擇流程Fig.4 Flow chart of unsupervised band selection for hyperspectral image using the Wasserstein metric-based configuration entropy

3 Wasserstein配置熵用于高光譜圖像非監督波段選擇的有效性評價

選取兩組試驗數據，比較W熵和7種熵圖像分類的精度。

3.1 試驗數據與評價流程

試驗數據為文獻[31]的印度松木試驗場(Indian Pines)高光譜數據(145×145像素，含220個波段)和文獻[32]的帕維亞大學(Pavia University)高光譜數據(610×340像素，含103個波段)(圖5)。

W熵有效性評價流程圖如圖6所示。

從最優波段圖像中隨機選取5%、10%和50%的像元作為各類地物的訓練集，余下像元作為測試集。使用支持向量機分類器對樣本進行分類(參數C設為1、核函數設為線性函數)[33]。為保證結果可比，各類地物訓練樣本數相同且隨機種子點也完全一致。

圖5 兩組高光譜圖像及其參考圖像與光譜特征Fig.5 Two hyperspectral images, their corresponding reference images and spectral characteristics

3.2 結果與分析

圖7為各信息熵指標在多種波段組合下對應的圖像分類精度。I為互信息、I1-I4為4種標準化的互信息、SID1和SID2為兩種相對熵變體、DW4和DW8分別為基于四鄰域和八鄰域的W熵差異值。

將Indian Pines和Pavia University的每類訓練樣本容量分別設為20和100。圖7表明，隨波段選擇個數增加，分類精度穩定提升。對Indian Pines數據有：①基于W熵差異值的圖像分類精度與穩定性均優于香農熵，特別是當選擇的波段數較少時。例如，當波段選擇個數為15、25和50時，基于W熵差異值的分類精度分別比互信息提高16%、18%和11%；②DW4和DW8的分類結果相近。當訓練樣本占比5%或10%，每類訓練樣本數量相同且波段個數為107—173時，DW8的分類精度高于DW4約3%。

對Pavia University數據有：①或許因訓練樣本規模不夠，當各類訓練樣本數量相同時，隨波段選擇個數增加，分類精度波動劇烈；②當訓練樣本占比為5%、10%和50%且波段選擇數較少時，基于W熵差異值的分類精度均優于互信息。選擇15個波段時，前者比后者分類精度高約4%；③樣本規模固定時，隨波段個數增加，基于互信息、相對熵變體及DW4指標的分類精度穩定提升；④當波段選擇個數為11—27時，DW8的分類精度比DW4高約2%。

為進一步比較波段選擇數量一定時具體入選波段的差異，將兩組數據在分類精度達到穩定時的最小波段數，即25和15作為閾值，分析基于互信息(I)、第1種相對熵變體(SID1)和DW8時的波段序號及其對應的光譜值。結果如圖8和表2所示。圖8中實線代表地物類別，虛線代表具體選擇波段序號。

圖9繪出了表2中各波段的W8dist值，可見基于DW8指標選出的波段信息更加豐富。

由圖8可知，Indian Pines數據在總波段數為1—50、60—70、110—130及170—190時分類效果較好。基于W熵差異值選出的前25個波段多位于上述區間內，而基于互信息和相對熵變體所選波段集中于100—110和150—170。并且，基于W熵差異值選出的前25個波段分布更離散、冗余度更低。Pavia University數據的分析結果一致。

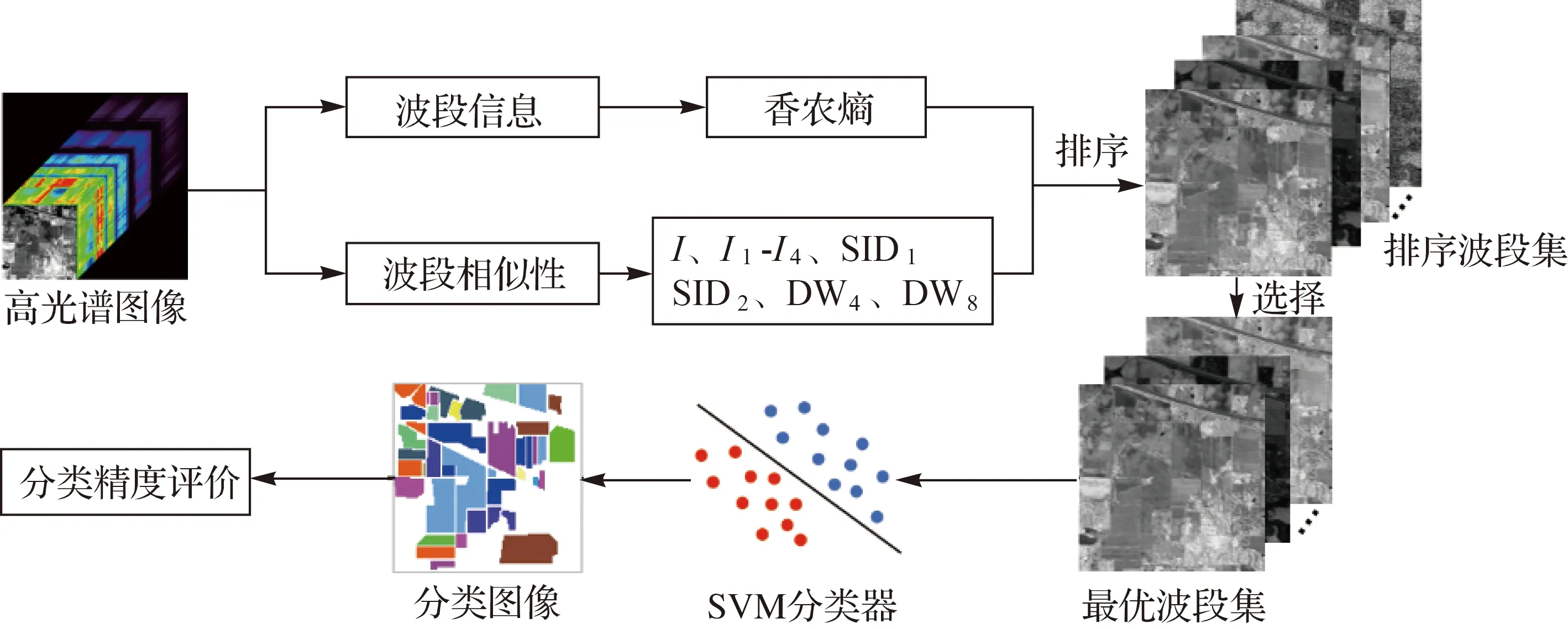
圖6 基于Wasserstein配置熵的高光譜圖像分類有效性評價流程Fig.6 Flow chart of evaluation on hyperspectral image classification using the Wasserstein metric-based configuration entropy

圖7 基于不同測度指標的波段組合的圖像分類精度Fig.7 Accuracy of image classification for band combinations using different indicators

圖10給出當訓練樣本占比為5%時，基于DW4和DW8選擇的Indian Pines第107至173個波段(該區間內DW4和DW8的分類精度差異顯著)，以及Pavia University第11至27個波段的光譜信息。

圖8 給定波段選擇個數下不同熵測度指標選出的波段序號及其光譜值Fig.8 Various entropy-based band selection and corresponding spectral value with given number of selected bands

表2 給定波段選擇個數下不同測度指標選出的波段序號

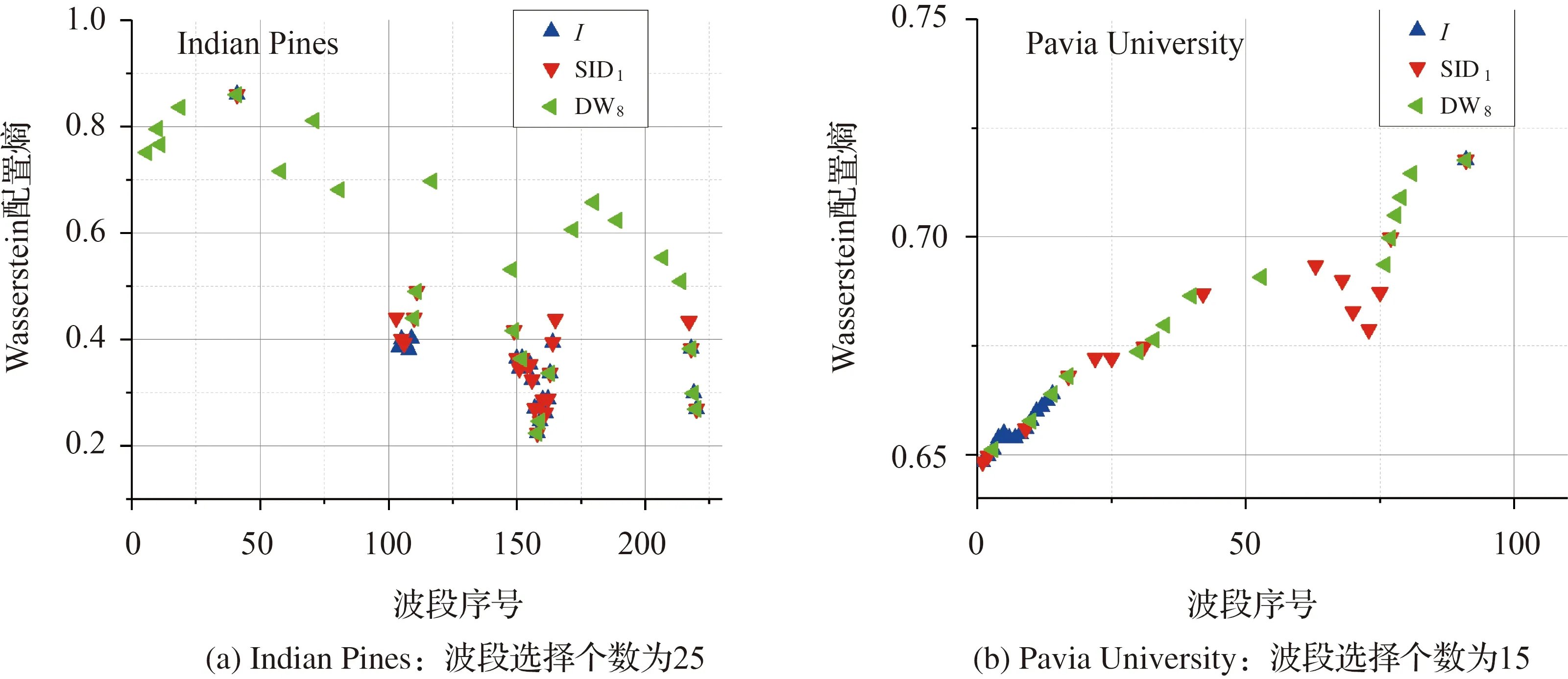
圖9 給定波段數目下基于不同指標選取得到的波段序號及其對應的Wasserstein配置熵Fig.9 Various entropy-based band selection and corresponding W8dist with given number of selected bands

圖10說明DW8挑選合適波段的能力優于DW4。例如，對Indian Pines數據，其第150至162個波段含有大量噪聲。DW4將第150、154和157號波段作為最優波段，而DW8只含有第154和157波段。Pavia University數據也證實DW8篩選最優波段的能力更強。

將SVM分類器更換為決策樹(decision tree，DT)分類器，其余條件不變，得到的結果見圖11。發現使用SVM分類器，DW8的分類精度均優于DW4。而使用DT分類器，DW8與DW4的分類精度相近。

圖10 基于DW4和DW8方法選取的部分波段信息Fig.10 Information of selected bands based on DW4 and DW8

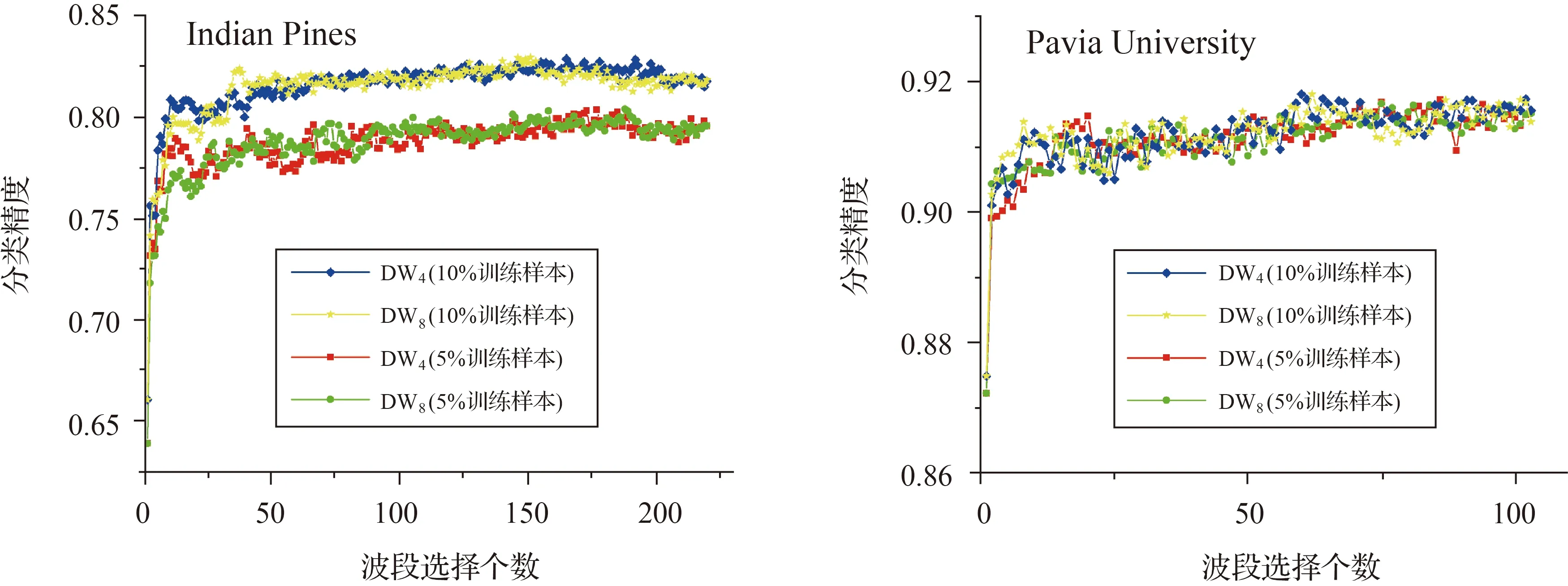
圖11 基于DW4和DW8的決策樹分類方法分類精度Fig.11 Accuracy of image classification of DW4 and DW8 using decision tree classifier

4 結 論

高光譜圖像應用前景廣泛，但其波段數量多且相鄰波段之間的相關性較高，需要根據波段信息和波段間相關性等進行波段選擇。以香農熵為代表的傳統信息熵測度指標僅考慮統計信息和空間組分信息，忽略了空間配置信息。玻爾茲曼熵能有效刻畫空間配置信息，特別是W熵還能消除連續空間的冗余信息。本文將傳統W熵從四鄰域拓展到八鄰域，提出了基于W熵差異值的高光譜圖像非監督次優波段選擇方法。以兩組高光譜圖像數據為例，比較了不同訓練樣本規模、不同波段選擇個數下，基于9種信息熵測度指標(兩種W熵差異值、互信息、四種標準化互信息和兩種相對熵變體)的圖像分類精度。結果表明，W熵差異值可用于高光譜圖像波段選擇和圖像分類，特別是當波段選擇個數較少時。八鄰域效果優于四鄰域。

W熵在不同場景下影像解譯的有效性仍待檢驗。W熵有望用于其他類型數據，如夜間燈光數據、土地利用數據、醫學影像等。此外，集成W熵和香農熵的影像復雜性測度模型也值得進一步探索。