例說(shuō)用特殊化方法探求定值
李潤(rùn)林

【摘要】在某些幾何圖形中,有些點(diǎn)或直線(xiàn)(射線(xiàn)、線(xiàn)段)的位置是不斷變化的,在這個(gè)變化過(guò)程中,有一些位置關(guān)系(如兩直線(xiàn)的平行或垂直)或數(shù)量關(guān)系(如線(xiàn)段的長(zhǎng)度、角的大小、弧的大小、線(xiàn)段的比等)卻始終保持不變,這就是幾何中的定值問(wèn)題.
【關(guān)鍵詞】特殊化方法;探求定值
圖1例1 已知:如圖1所示,在△ABC中,AB=AC,P是BC上任意一點(diǎn),PR⊥AB,PQ⊥AC,BD⊥AC,垂足分別為R,Q,D.求證:PQ+PR為定值.
分析 因?yàn)镻是BC上任意一點(diǎn)(即P是動(dòng)點(diǎn)),所以當(dāng)P運(yùn)動(dòng)到B的位置時(shí),R和Q也隨之分別運(yùn)動(dòng)到B和D的位置,此時(shí)PR=0,PQ=BD,由此猜想BD就是所要求的定值.
下面我們來(lái)證明這個(gè)猜想在一般情況下也是正確的.
分析 因?yàn)镻是△ABC內(nèi)任意一點(diǎn)(即P是動(dòng)點(diǎn)),所以當(dāng)P運(yùn)動(dòng)到△ABC的重心位置時(shí)(圖7),由“等腰三角形頂角的平分線(xiàn)、底邊上的高、底邊上的中線(xiàn)互相重合”及“角平分線(xiàn)上的點(diǎn)到已知角兩邊的距離相等”知PD=PE=PF=1[]3AD,于是我們猜想PD+PE+PF=AD=3[]2m就是所要求的定值.
分析 當(dāng)正方形A1B1C1O繞點(diǎn)O旋轉(zhuǎn)到特殊位置(圖10)時(shí),容易證明重疊部分是一個(gè)邊長(zhǎng)為1[]2的小正方形,其面積為1[]4,由此我們猜想圖9中重疊部分四邊形OEBF的面積等于1[]4就是所要求的定值.
下面我們來(lái)證明這個(gè)猜想在一般情況下也是正確的.
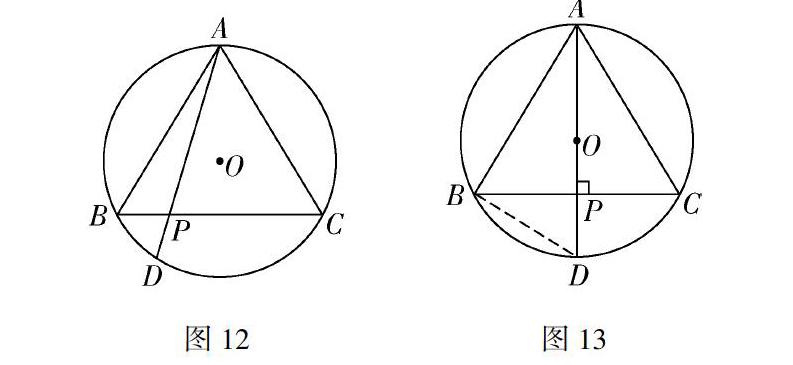
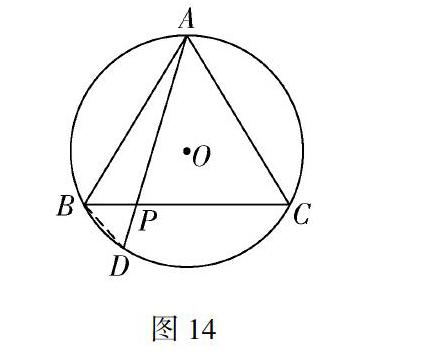
分析 由于點(diǎn)P是BC邊上的一個(gè)動(dòng)點(diǎn),所以當(dāng)點(diǎn)P運(yùn)動(dòng)到BC的中點(diǎn)位置(如圖13)時(shí),由AB=AC、“等腰三角形頂角的平分線(xiàn)、底邊上的高、底邊上的中線(xiàn)互相重合”及“垂徑定理”的推論知AD是⊙O的直徑,且∠APB=90°.連接BD,則易證△APB∽△ABD,于是AP[]AB=AB[]AD,從而猜想AP·AD=AB2就是所要求的定值.
下面我們來(lái)證明這個(gè)猜想在一般情況下也是正確的.
綜上所述,在求解幾何定值問(wèn)題時(shí),確定定值等于多少是解決問(wèn)題的關(guān)鍵,其一般方法是:通過(guò)分析特殊位置情況下的圖形先猜想出定值,然后在一般的位置情況下證明猜想成立.也就是說(shuō),解決定值問(wèn)題一般有如下兩個(gè)步驟:
(1)在特殊位置下探求定值;
(2)在一般情況下證明結(jié)論.

